2021-2022学年高一下学期数学北师大版(2019)必修第二册4.2两角和与差的三角函数公式(复习课)课件(37张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册4.2两角和与差的三角函数公式(复习课)课件(37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 20:15:19 | ||
图片预览









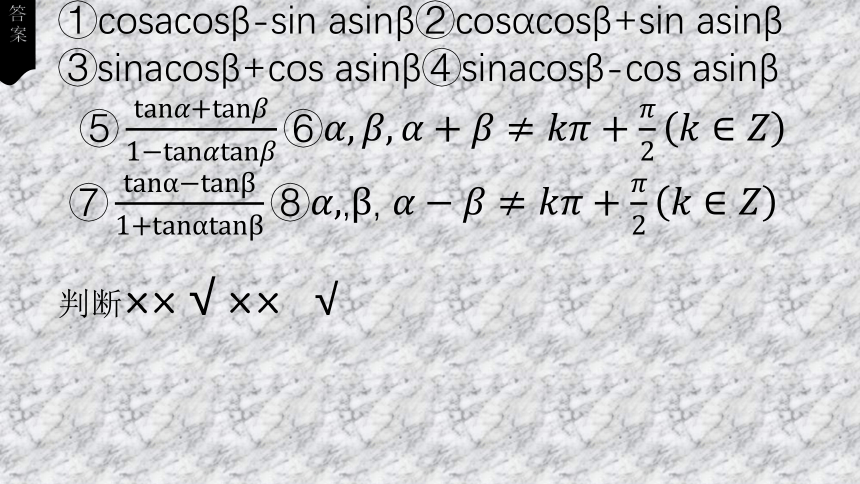

文档简介
(共37张PPT)
4.2两角和与差的三角函数公式
(复习课)
北师大(2019)必修2
1.掌握两角和与差的正弦、余弦、正切公式及其变形.
2.掌握三角函数的叠加及其应用
3.了解积化和差与和差化积公式及其应用
4.能够运用三角函数公式解决化简、求值与证明等问
基础知识梳理与理解
学以致用
题型分类 深度剖析
内容索引
基础知识梳理与理解
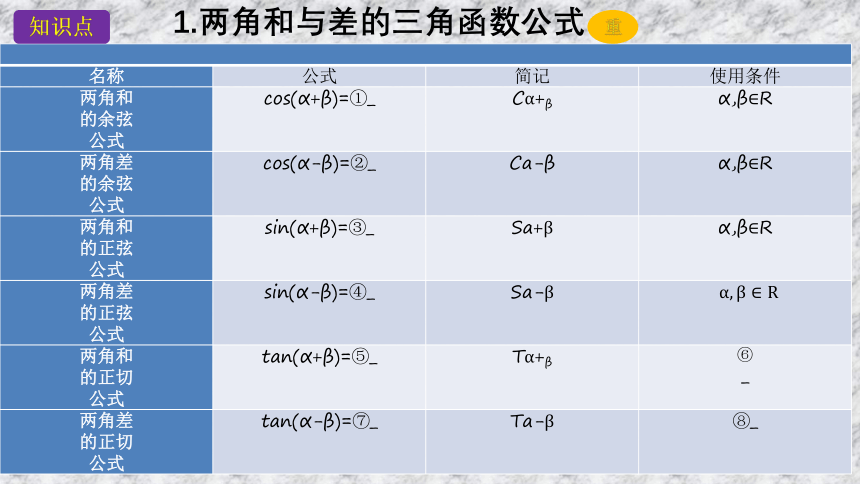
名称 公式 简记 使用条件
两角和 的余弦 公式 cos(α+β)=①_ Cα+β α,β∈R
两角差 的余弦 公式 cos(α-β)=②_ Ca-β α,β∈R
两角和 的正弦 公式 sin(α+β)=③_ Sa+β α,β∈R
两角差 的正弦 公式 sin(α-β)=④_ Sa-β
两角和 的正切 公式 tan(α+β)=⑤_ Tα+β ⑥
_
两角差 的正切 公式 tan(α-β)=⑦_ Ta-β ⑧_
知识点
1.两角和与差的三角函数公式
重
知识点
2.两角和与差的正切公式的变形
(1) tanα+tanβ=tan(α+β)(1-tanαtan β);
(2)tanα-tanβ =tan(α-β)(1+tanαtan β).
α
知识点
3.三角函数的叠加
asinα+bcosα=⑨__ sin(α+φ),其中
sinφ=⑩ _,cosφ=11__(a,b不同时为0).
重
知识点
4.积化和差与和差化积公式
(1)积化和差公式
知识点
4.积化和差与和差化积公式
(2)和差化积公式
判断正误
正确的画“√”,错误的画“×”
1.对于任意角α,β,都有cos(α+β)=cosα+cosβ.()
2.不存在角α,β,使得cos(α-β)=cosαcosβ-sinα·sinβ.()
3.若α,β为锐角,则sin(α+β)可以根据公式Tα+β,直接展开().
+ )(a,b不同时为0)中的φ是唯一的()
()
①cosacosβ-sin asinβ②cosαcosβ+sin asinβ
③sinacosβ+cos asinβ④sinacosβ-cos asinβ
,β,
判断××√×× √
答案t
题型分类 深度剖析
第1 利用公式解决给角求值问题
第2 利用公式解决给值求值问题
第3 利用公式解决给值求角问题
第3 利用三角函数的叠加研究函数性质
利用公式解决给角求值问题
利用公式解决给角求值问题的关键是通过公式的合理运用,使所求式中的非特殊角转化为特殊角,或使式中出现可以正负抵消的项,或使式中出现分子、分母能约分的项,从而达到化简求值的目的.具体注意以下几点:
(1)看角:把角尽量向特殊角或可计算的角转化,合理拆角,化异为同;
(2)看名称:把式子中的三角函数的名称尽量化成同一名称或相近的名称,例如可以把正切函数化为正、余弦函数,或把正、余弦函数转化为正切函数,再解决问题;
(3)看式子:看式子是否满足两角和与差的正弦、余弦、正切公式,准确选择公式求解.
讲解
利用公式解决给角求值问题
求sin 37.5°cos7.5°的值为()
例题
解.C sin 37.
计算 ()
C.2 D.4
原式
故选C.
利用公式解决给值求值问题
给值求值,即由给出的某些角的三角函数值,求另外一些角的三角函数值,关键在“变角”,使“所求角”变为“已知角”,常见的技巧如下:
(1)当“已知角”有两个时,“所求角”一般表示为两个已知角的和或差的形式;
(2)当“已知角”有一个时,应注意“已知角”与“所求角”的关系,通过诱导公式或引入特殊角,将“所求角”变成“已知角”;
(3)配角技巧:
β-(β-α),
讲解
利用公式解决给值求值问题
已知
(1)求sin(a+β)的值;
(2)求cos(α-β)的值;
(3)求tanα的值.
例题
思路点拨
(1)由于 sin(a+β)=-sin(π+α+β),因此只需求出 的值即可;(2)由于 因此要求
cos(α-β)的值可通过求 )]的值得到;(3)利用tan α= 求解
解析(1)因为 所以 因为 所以 因此 (π+α+β)]
=
解析(1)因为 所以 因为 所以 因此 (π+α+β)]
=
(2)由(1)可知,
所以
=-cos(α-β),所
(3)由(1)可得 于是 =7
利用公式解决给值求角问题
1.解决给值求角问题的一般步骤:
(1)求角的某一个三角函数值;(2)确定角的范围;(3)根据角的范围写出所求的角.
2.通过求角的某个三角函数值来求角,选取函数是关键,一般遵循以下原则:
(1)已知正切函数值,选取正切函数.
(2)已知正弦、余弦函数值,选取正弦函数或余弦函数;若角的范围是(0, ),选正弦函数、余弦函数均可;若角的范围是(0,π),选余弦函数较好;若角的范围选正弦函数较好.
讲解
利用公式解决给值求角问题
(1)已知 且α,β∈(0,π),求α+β的值;
(2)已知 且α∈
求α+β的值;
(3)已知 且α,β∈(0,π),求2α-β的值.
例题
解析(1)由 且α,β∈ )可得COS
因此
又因为 所以α+β∈(0,π),
故
(2)因为 且
所以
因此sin(α+β)=
又因为
所以 故
=1
利用三角函数的叠加研究函数性质
1.asin 其中sinφb不同时为0);
asin 其中sinφ b不同时为0).
作用:将形如asinα+bcosα(a,b不同时为0)的三角函数式转化为Asin(α+φ)(或Acos(α+φ))的形式,以利于研究这类函数的图象和性质.
讲解
(2)形式选择:
化为正弦还是余弦,要由具体条件而定,一般要求变形后角α的系数为正,这样更有利于研究函数的性质.
2.应用三角函数解决实际问题的关键是合理引入辅助角,确定各量之间的关系,将实际问题转化为三角函数问题,再利用三角函数的有关知识求解.
3.在求解过程中,要注意三点:
(1)充分借助平面几何性质,寻找数量关系;
(2)注意实际问题中变量的取值范围;
(3)注意三角函数有界性的影响.
利用三角函数的叠加研究函数性质
已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则tanφ的值为()
A.-2 D.2
例题
若 则函数 的值可以为()
C.3 D.4
函数f(x)=Asin(ωx+φ)的部分图象如图所示.
(1)求(x)的最小正周期及解析式;
()设函数g(x)=f(x)-cos2x,求 上的最小值. g(x)在区间
4.2两角和与差的三角函数公式
(复习课)
北师大(2019)必修2
1.掌握两角和与差的正弦、余弦、正切公式及其变形.
2.掌握三角函数的叠加及其应用
3.了解积化和差与和差化积公式及其应用
4.能够运用三角函数公式解决化简、求值与证明等问
基础知识梳理与理解
学以致用
题型分类 深度剖析
内容索引
基础知识梳理与理解
名称 公式 简记 使用条件
两角和 的余弦 公式 cos(α+β)=①_ Cα+β α,β∈R
两角差 的余弦 公式 cos(α-β)=②_ Ca-β α,β∈R
两角和 的正弦 公式 sin(α+β)=③_ Sa+β α,β∈R
两角差 的正弦 公式 sin(α-β)=④_ Sa-β
两角和 的正切 公式 tan(α+β)=⑤_ Tα+β ⑥
_
两角差 的正切 公式 tan(α-β)=⑦_ Ta-β ⑧_
知识点
1.两角和与差的三角函数公式
重
知识点
2.两角和与差的正切公式的变形
(1) tanα+tanβ=tan(α+β)(1-tanαtan β);
(2)tanα-tanβ =tan(α-β)(1+tanαtan β).
α
知识点
3.三角函数的叠加
asinα+bcosα=⑨__ sin(α+φ),其中
sinφ=⑩ _,cosφ=11__(a,b不同时为0).
重
知识点
4.积化和差与和差化积公式
(1)积化和差公式
知识点
4.积化和差与和差化积公式
(2)和差化积公式
判断正误
正确的画“√”,错误的画“×”
1.对于任意角α,β,都有cos(α+β)=cosα+cosβ.()
2.不存在角α,β,使得cos(α-β)=cosαcosβ-sinα·sinβ.()
3.若α,β为锐角,则sin(α+β)
+ )(a,b不同时为0)中的φ是唯一的()
()
①cosacosβ-sin asinβ②cosαcosβ+sin asinβ
③sinacosβ+cos asinβ④sinacosβ-cos asinβ
,β,
判断××√×× √
答案t
题型分类 深度剖析
第1 利用公式解决给角求值问题
第2 利用公式解决给值求值问题
第3 利用公式解决给值求角问题
第3 利用三角函数的叠加研究函数性质
利用公式解决给角求值问题
利用公式解决给角求值问题的关键是通过公式的合理运用,使所求式中的非特殊角转化为特殊角,或使式中出现可以正负抵消的项,或使式中出现分子、分母能约分的项,从而达到化简求值的目的.具体注意以下几点:
(1)看角:把角尽量向特殊角或可计算的角转化,合理拆角,化异为同;
(2)看名称:把式子中的三角函数的名称尽量化成同一名称或相近的名称,例如可以把正切函数化为正、余弦函数,或把正、余弦函数转化为正切函数,再解决问题;
(3)看式子:看式子是否满足两角和与差的正弦、余弦、正切公式,准确选择公式求解.
讲解
利用公式解决给角求值问题
求sin 37.5°cos7.5°的值为()
例题
解.C sin 37.
计算 ()
C.2 D.4
原式
故选C.
利用公式解决给值求值问题
给值求值,即由给出的某些角的三角函数值,求另外一些角的三角函数值,关键在“变角”,使“所求角”变为“已知角”,常见的技巧如下:
(1)当“已知角”有两个时,“所求角”一般表示为两个已知角的和或差的形式;
(2)当“已知角”有一个时,应注意“已知角”与“所求角”的关系,通过诱导公式或引入特殊角,将“所求角”变成“已知角”;
(3)配角技巧:
β-(β-α),
讲解
利用公式解决给值求值问题
已知
(1)求sin(a+β)的值;
(2)求cos(α-β)的值;
(3)求tanα的值.
例题
思路点拨
(1)由于 sin(a+β)=-sin(π+α+β),因此只需求出 的值即可;(2)由于 因此要求
cos(α-β)的值可通过求 )]的值得到;(3)利用tan α= 求解
解析(1)因为 所以 因为 所以 因此 (π+α+β)]
=
解析(1)因为 所以 因为 所以 因此 (π+α+β)]
=
(2)由(1)可知,
所以
=-cos(α-β),所
(3)由(1)可得 于是 =7
利用公式解决给值求角问题
1.解决给值求角问题的一般步骤:
(1)求角的某一个三角函数值;(2)确定角的范围;(3)根据角的范围写出所求的角.
2.通过求角的某个三角函数值来求角,选取函数是关键,一般遵循以下原则:
(1)已知正切函数值,选取正切函数.
(2)已知正弦、余弦函数值,选取正弦函数或余弦函数;若角的范围是(0, ),选正弦函数、余弦函数均可;若角的范围是(0,π),选余弦函数较好;若角的范围选正弦函数较好.
讲解
利用公式解决给值求角问题
(1)已知 且α,β∈(0,π),求α+β的值;
(2)已知 且α∈
求α+β的值;
(3)已知 且α,β∈(0,π),求2α-β的值.
例题
解析(1)由 且α,β∈ )可得COS
因此
又因为 所以α+β∈(0,π),
故
(2)因为 且
所以
因此sin(α+β)=
又因为
所以 故
=1
利用三角函数的叠加研究函数性质
1.asin 其中sinφb不同时为0);
asin 其中sinφ b不同时为0).
作用:将形如asinα+bcosα(a,b不同时为0)的三角函数式转化为Asin(α+φ)(或Acos(α+φ))的形式,以利于研究这类函数的图象和性质.
讲解
(2)形式选择:
化为正弦还是余弦,要由具体条件而定,一般要求变形后角α的系数为正,这样更有利于研究函数的性质.
2.应用三角函数解决实际问题的关键是合理引入辅助角,确定各量之间的关系,将实际问题转化为三角函数问题,再利用三角函数的有关知识求解.
3.在求解过程中,要注意三点:
(1)充分借助平面几何性质,寻找数量关系;
(2)注意实际问题中变量的取值范围;
(3)注意三角函数有界性的影响.
利用三角函数的叠加研究函数性质
已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则tanφ的值为()
A.-2 D.2
例题
若 则函数 的值可以为()
C.3 D.4
函数f(x)=Asin(ωx+φ)的部分图象如图所示.
(1)求(x)的最小正周期及解析式;
()设函数g(x)=f(x)-cos2x,求 上的最小值. g(x)在区间
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
