2021-2022学年人教版八年级数学下册18.1.1平行四边形的性质课件 (共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1.1平行四边形的性质课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 16:29:47 | ||
图片预览





文档简介
(共18张PPT)
18.1.1 平行四边形的性质
八年级数学下册
学习目标
学习重、难点
1.能画平行四边形,会用符号表示平行四边形.
2.能证明并运用“平行四边形对边相等、对角相等”的性质.
重点:平行四边形的定义及性质.
难点:运用性质解题.
这些都是日常生活中常见的情形,他们是否都有平行四边形的现象?
新课导入
这些图形都有平行四边形的形象.
拿出剪好的两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个怎样的四边形?
探究一:动手操作
A
B
C
D
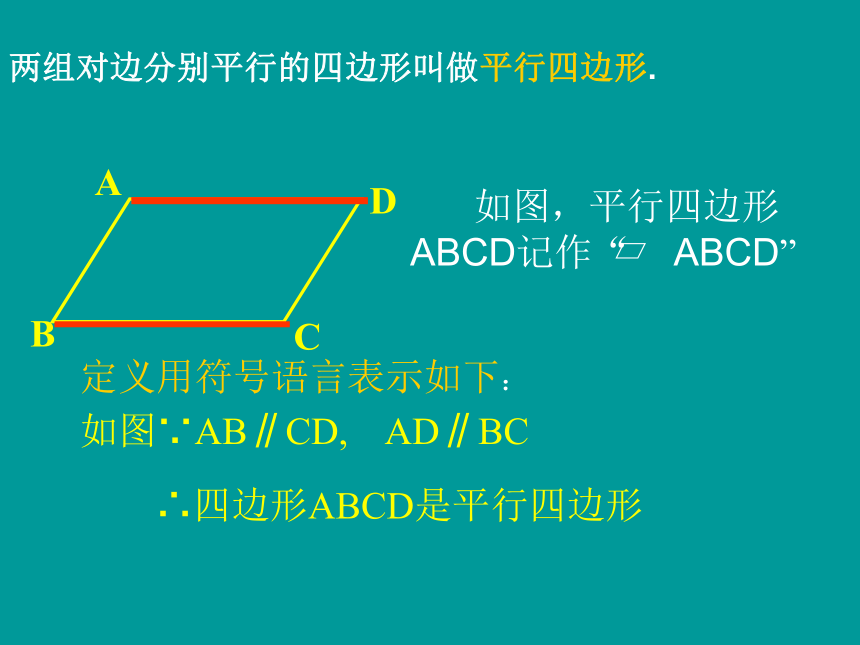
两组对边分别平行的四边形叫做平行四边形.
如图,平行四边形ABCD记作“ ABCD”
∴四边形ABCD是平行四边形
如图∵AB∥CD, AD∥BC
定义用符号语言表示如下:
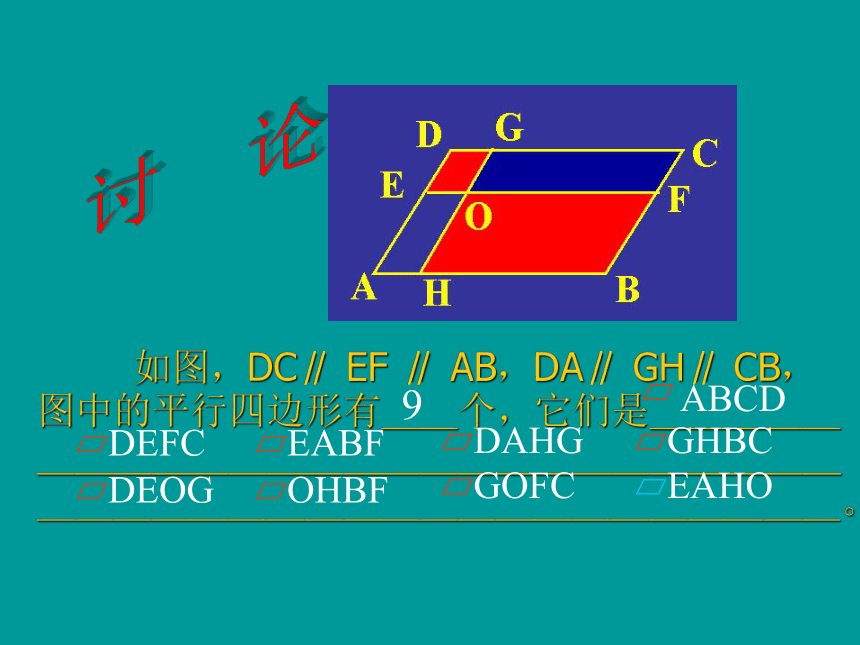
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。
讨 论
ABCD
EAHO
GOFC
OHBF
DEOG
GHBC
DAHG
EABF
DEFC
9
D
A
B
C
O
H
E
F
G
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
探究二:画一画
平行四边形的对边还有怎样的关系
平行四边形的对角有怎样的关系
两组对边
分别平行
四边形
猜想
观察
平行四边形
平行四边形:
两组对边分别相等
两组对角分别相等
探索
合作交流,想方设法验证
B
C
D
A
推理
A
B
C
D
1
2
3
4
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC, AB∥CD
∴∠1=∠2, ∠3=∠4
∴∠BAD=∠BCD
在△ABC和△CDA中
∠1=∠2
AC=CA
∠3=∠4
∴△ABC≌△CDA
∴AD=BC, AB=DC, ∠B=∠D
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
已知:四边形ABCD是平行四边形.求
证:AD=BC,AB=CD,∠BAD=∠BCD,
∠B=∠D
思考 不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
思考
平行四边形的对边相等.
平行四边形的性质除了对边互相平行以外,还有:
A
B
C
D
归纳总结
平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴AD=BC,AB =CD
∴AD∥BC,AB ∥ CD
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
A
D
B
C
解:
∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
1.如图,四边形ABCD是平行四边形,填空
(1) ∠ADC=__,∠BCD=__
(2) ABCD的周长=____
试一试
B
A
D
C
5
3
50°
50°
130°
16
2.一个平行四边形的一个外 角是38°,这个平行四边形的每个内角的度数分别是多少?为什么?
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
从拼图可以得到什么启示?
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两组对角分别相等,邻角互补
课堂小结
课后作业
习题18.1第 2、3题
18.1.1 平行四边形的性质
八年级数学下册
学习目标
学习重、难点
1.能画平行四边形,会用符号表示平行四边形.
2.能证明并运用“平行四边形对边相等、对角相等”的性质.
重点:平行四边形的定义及性质.
难点:运用性质解题.
这些都是日常生活中常见的情形,他们是否都有平行四边形的现象?
新课导入
这些图形都有平行四边形的形象.
拿出剪好的两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个怎样的四边形?
探究一:动手操作
A
B
C
D
两组对边分别平行的四边形叫做平行四边形.
如图,平行四边形ABCD记作“ ABCD”
∴四边形ABCD是平行四边形
如图∵AB∥CD, AD∥BC
定义用符号语言表示如下:
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。
讨 论
ABCD
EAHO
GOFC
OHBF
DEOG
GHBC
DAHG
EABF
DEFC
9
D
A
B
C
O
H
E
F
G
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
探究二:画一画
平行四边形的对边还有怎样的关系
平行四边形的对角有怎样的关系
两组对边
分别平行
四边形
猜想
观察
平行四边形
平行四边形:
两组对边分别相等
两组对角分别相等
探索
合作交流,想方设法验证
B
C
D
A
推理
A
B
C
D
1
2
3
4
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC, AB∥CD
∴∠1=∠2, ∠3=∠4
∴∠BAD=∠BCD
在△ABC和△CDA中
∠1=∠2
AC=CA
∠3=∠4
∴△ABC≌△CDA
∴AD=BC, AB=DC, ∠B=∠D
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
已知:四边形ABCD是平行四边形.求
证:AD=BC,AB=CD,∠BAD=∠BCD,
∠B=∠D
思考 不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
思考
平行四边形的对边相等.
平行四边形的性质除了对边互相平行以外,还有:
A
B
C
D
归纳总结
平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴AD=BC,AB =CD
∴AD∥BC,AB ∥ CD
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
A
D
B
C
解:
∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
1.如图,四边形ABCD是平行四边形,填空
(1) ∠ADC=__,∠BCD=__
(2) ABCD的周长=____
试一试
B
A
D
C
5
3
50°
50°
130°
16
2.一个平行四边形的一个外 角是38°,这个平行四边形的每个内角的度数分别是多少?为什么?
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
从拼图可以得到什么启示?
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两组对角分别相等,邻角互补
课堂小结
课后作业
习题18.1第 2、3题
