第三章 圆的“三大定理”专项训练(含解析)
文档属性
| 名称 | 第三章 圆的“三大定理”专项训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 19:45:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学圆的“三大定理”
一.切割线定理
1.已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R= cm.
2.如图,在△ABC中,AB=AC,∠C=72°,⊙O过AB两点且与BC切于B,与AC交于D,连接BD,若BC=﹣1,则AC= .
3.如图,A,B,D,E四点在⊙O上,AE,BD的延长线相交于点C,直径AE为8,OC=12,∠EDC=∠BAO.
(1)求证:;
(2)计算CD CB的值,并指出CB的取值范围.
4.如图,⊙O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到P,过P作⊙O的切线,切点为C,若PC=2,求PD的长.
5.如图,PA是⊙O的切线,A为切点,PBC是过点O的割线.若PA=8cm,PB=4cm,则⊙O的直径为( )
A.6cm B.8cm C.12cm D.16cm
二.弦切角定理
6.如图,AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
7.如图PA切⊙O于点A,∠PAB=30°,则∠AOB= 度,∠ACB= 度.
8.如图,A、B为⊙O上的点,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D,若AC为∠BAD的平分线.
求证:(1)AB为⊙O的直径;(2)AC2=AB AD.
9.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于点C,AE⊥CE且交⊙O于点D.
求证:(1)DC=BC;
(2)BC2=AB DE.
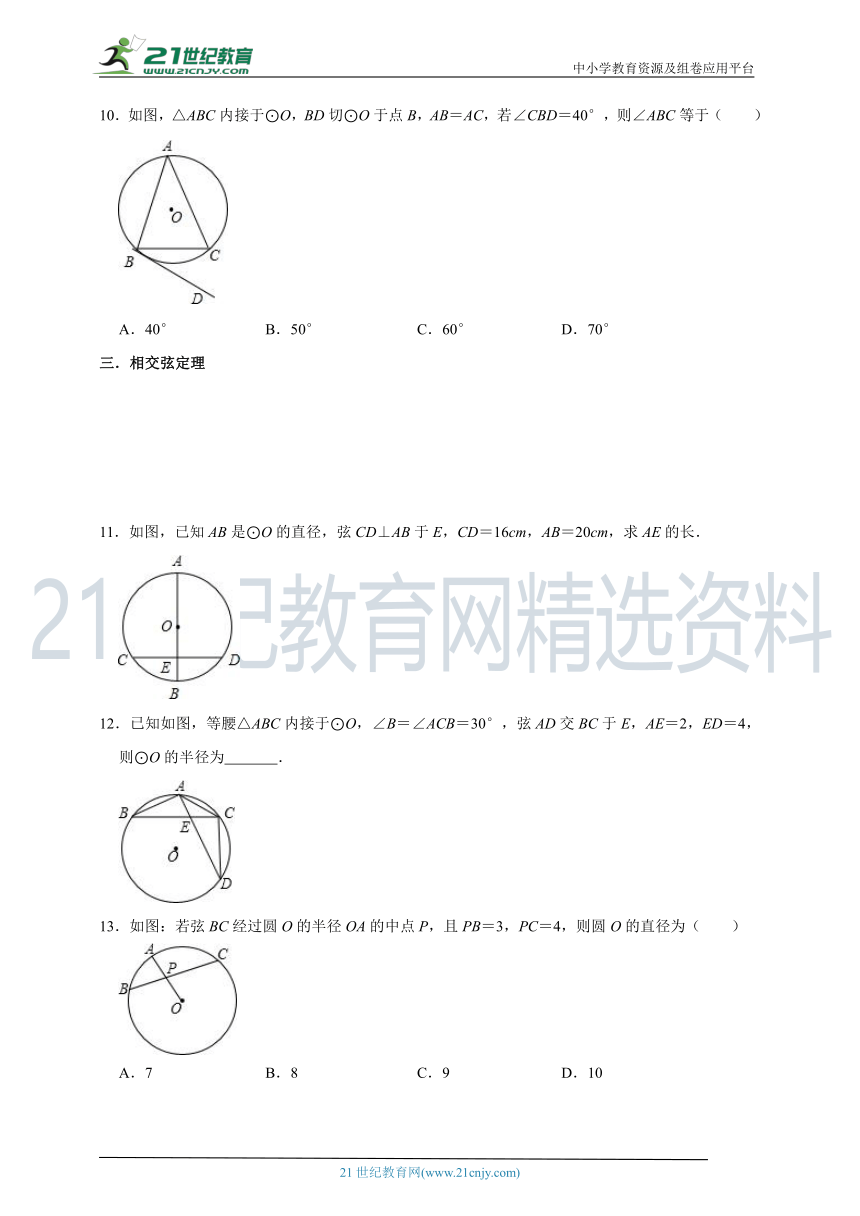
10.如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于( )
A.40° B.50° C.60° D.70°
三.相交弦定理
11.如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,求AE的长.
12.已知如图,等腰△ABC内接于⊙O,∠B=∠ACB=30°,弦AD交BC于E,AE=2,ED=4,则⊙O的半径为 .
13.如图:若弦BC经过圆O的半径OA的中点P,且PB=3,PC=4,则圆O的直径为( )
A.7 B.8 C.9 D.10
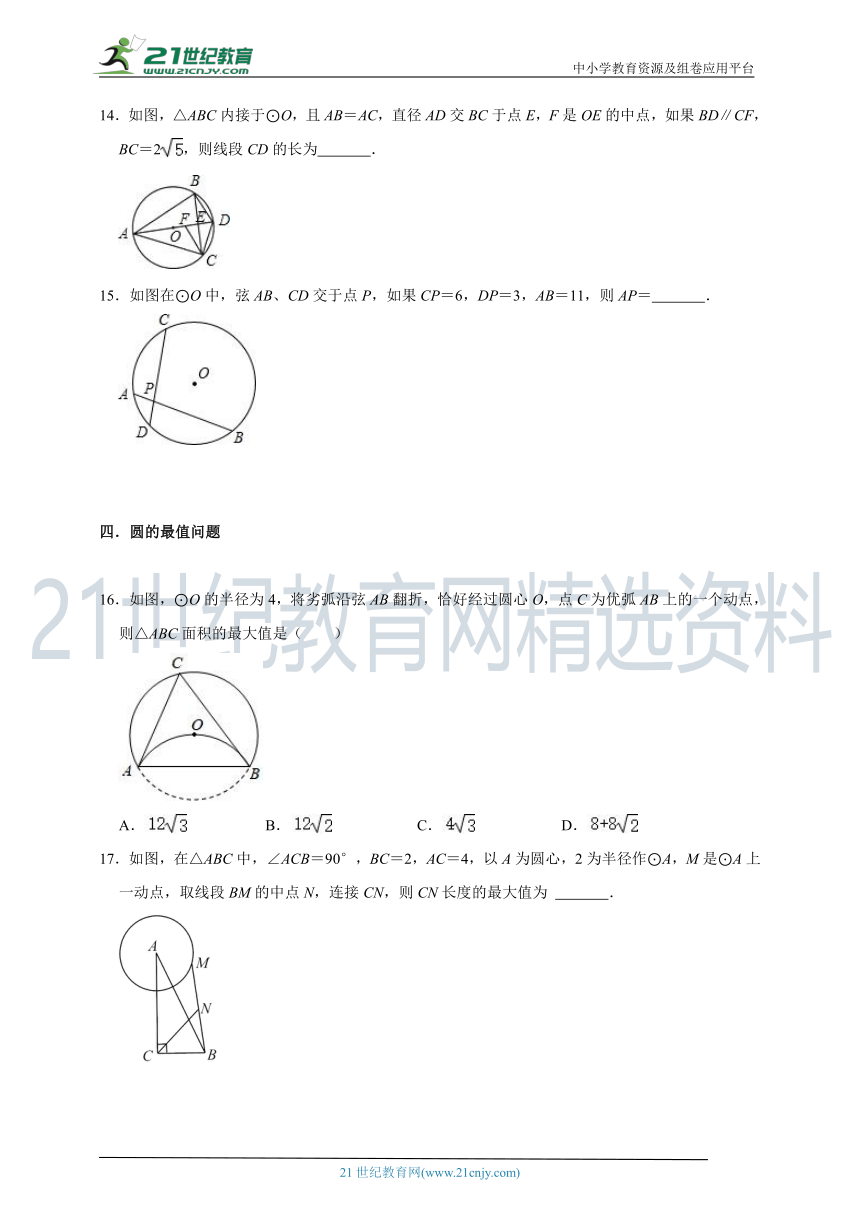
14.如图,△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE的中点,如果BD∥CF,BC=2,则线段CD的长为 .
15.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP= .
四.圆的最值问题
16.如图,⊙O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是( )
A. B. C. D.
17.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,以A为圆心,2为半径作⊙A,M是⊙A上一动点,取线段BM的中点N,连接CN,则CN长度的最大值为 .
参考答案与试题解析
一.试题(共20小题)
1.已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R= cm.
【解答】解:∵PC是切线,
∴PC2=PA PB;
又∵PC=4,PA=3,
∴16=3(3+AB),
∴AB=,
∴半径R=.
2.如图,在△ABC中,AB=AC,∠C=72°,⊙O过AB两点且与BC切于B,与AC交于D,连接BD,若BC=﹣1,则AC= 2 .
【解答】解:∵AB=AC,∠C=72°,BC是⊙O的切线,
∴∠CBD=∠BAC=36°,
∴∠ABD=36°,
∴∠BDC=∠BCD=72°,
∴AD=BD=BC;
又∵BC是切线,
∴BC2=CD AC,
∴BC2=(AC﹣BC) AC(设AC=x),则可得到:(x﹣)2=,
解得:x1=2,x2=(x2<0不合题意,舍去).
∴AC=2.
3.如图,A,B,D,E四点在⊙O上,AE,BD的延长线相交于点C,直径AE为8,OC=12,∠EDC=∠BAO.
(1)求证:;
(2)计算CD CB的值,并指出CB的取值范围.
【解答】(1)证明:∵四边形ABDE内接于⊙O,
∴∠EDC=∠BAO,∠C=∠C,
∴△CDE∽△CAB,
∴;
(2)解:∵直径AE=8,OC=12,
∴AC=12+4=16,CE=12﹣4=8.
又∵=,
∴CD CB=AC CE=16×8=128.
连接OB,在△OBC中,OB=AE=4,OC=12,
故BC的范围是:8≤BC≤16.
4.如图,⊙O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到P,过P作⊙O的切线,切点为C,若PC=2,求PD的长.
【解答】解:(1)∵直径AB=10,弦DE⊥AB于点H,
∴DH=EH,
∴DH EH=AH BH=16,
∴DH=4,
∴DE=8;
(2)∵PC切⊙O于点C,
∴PC2=PD PE,
∵PC=2,
∴PD=2,或PD=﹣10(舍去),
∴PD=2.
5.如图,PA是⊙O的切线,A为切点,PBC是过点O的割线.若PA=8cm,PB=4cm,则⊙O的直径为( )
A.6cm B.8cm C.12cm D.16cm
【解答】解:∵PA2=PB PC,PA=8cm,PB=4cm,
∴PC=16cm,
∴BC=12cm.
故选:C.
6.如图,AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
【解答】解:∵AB是⊙O的直径,DE为⊙O的切线,∠CBE=40°,
∴∠A=∠CBE=40°.
故选:B.
7.如图PA切⊙O于点A,∠PAB=30°,则∠AOB= 60 度,∠ACB= 30 度.
【解答】解:由弦切角定理知,∠C=∠BAP=30°;
由圆周角定理知,∠AOB=2∠C=60°.
8.如图,A、B为⊙O上的点,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D,若AC为∠BAD的平分线.
求证:(1)AB为⊙O的直径;(2)AC2=AB AD.
【解答】证明:(1)连接BC,
AC平分∠BAD,
∴∠DAC=∠CAB.
又CD切⊙O于点C,
∴∠ACD=∠B(弦切角定理).
∵AD⊥CD,
∴∠ACD+∠DAC=90°.
即∠B+∠CAB=90°,∴∠BCA=90°.
∴AB是⊙O的直径(90°圆周角所对弦是直径).
(2)∵∠ACD=∠B,∠DAC=∠CAB,
∴△ACD∽△ABC.
∴.
∴AC2=AB AD.
9.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于点C,AE⊥CE且交⊙O于点D.
求证:(1)DC=BC;
(2)BC2=AB DE.
【解答】证明:(1)连接OC,
∵CE切圆O于点C,
∴∠ECO=90°,
∴∠E=∠ECO=90°,
∴AE∥CO,
∴∠DAC=∠ACO,
∴弧DC=弧BC,
∴DC=BC.
(2)∵弧DC=弧BC,CE切⊙O于C,
∴∠DCE=∠BAC.
又AB是⊙O直径,
∴∠CED=∠ACB=90°.
∴△DCE∽△BCA即=,而DC=BC.
∴BC2=AB DE.
10.如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于( )
A.40° B.50° C.60° D.70°
【解答】解:∵BD切⊙O于点B,
∴∠DBC=∠A=40°,
∵AB=AC,
∴∠ABC=∠C,
∴∠ABC=(180°﹣40°)÷2=70°.
故选:D.
11.如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,求AE的长.
【解答】解:根据垂径定理可知CE=8cm,
根据相交弦定理可得:
64=BE×AE=(AB﹣AE)×AE
解方程得:AE=16(cm).
12.已知如图,等腰△ABC内接于⊙O,∠B=∠ACB=30°,弦AD交BC于E,AE=2,ED=4,则⊙O的半径为 2 .
【解答】解:连接OA,OC,AO交BC于点F,则OA=OC,∠B=∠C,
∴AB=AC,
由圆周角定理知,∠O=2∠D=60°,
所以等腰△OAC是等边三角形,
有AB=AC=OA,
∵∠B=∠C,
∴AE⊥BC
∵AB=AC,AE=AE,
∴Rt△ABE≌Rt△ACE,
∴BE=CE,∠AEB=∠AEC,
∵∠AEB+∠AEC=180°,
∴∠AEB=∠AEC=90°,
∴BF2=AB2﹣AF2,AF2+EF2=AE2,
由相交弦定理知,BE CE=AE ED=8,
而BE CE=(BF+EF)(BF﹣EF)=BF2﹣EF2=AB2﹣AF2﹣EF2=AB2﹣AE2=AB2﹣4=8,
∴AB2=12,
∴半径等于2.
13.如图:若弦BC经过圆O的半径OA的中点P,且PB=3,PC=4,则圆O的直径为( )
A.7 B.8 C.9 D.10
【解答】解:延长AO交⊙O于点D,
设⊙O的半径是x,
根据相交弦定理,得=12,x=4,
因此⊙O的直径是8.
故选:B.
14.如图,△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE的中点,如果BD∥CF,BC=2,则线段CD的长为 .
【解答】解:连接BF,
∵BD∥CF,
∴∠FCB=∠DBC.
∵AB=AC,
∴=,=,
∴∠BCD=∠DBC,AD是BC的垂直平分线,
∴四边形DCFB是菱形,
∴∠FCB=∠DCB,CE为等腰三角形FCD的顶角平分线.
设ED=x,则AE=5x,故x 5x=()2,
解得x=1,x=﹣1(舍去).
根据勾股定理得:CD==.
15.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP= 2或9 .
【解答】解:根据相交弦定理,得:
AP PB=CP DP
∵AB=11
∴AP(11﹣AP)=CP DP
∴AP2﹣11AP+18=0
∴AP=2或9.
16.如图,⊙O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是( )
A. B. C. D.
【解答】解:如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO,AK.
由题意AB垂直平分线段OK,
∴AO=AK,
∵OA=OK,
∴OA=OK=AK,
∴∠OAK=∠AOK=60°.
∴AH=OA sin60°=4×=2,
∵OH⊥AB,
∴AH=BH,
∴AB=2AH=4,
∵OC+OH≥CT,
∴CT≤4+2=6,
∴CT的最大值为6,
∴△ABC的面积的最大值为××6=12,
故选:A.
17.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,以A为圆心,2为半径作⊙A,M是⊙A上一动点,取线段BM的中点N,连接CN,则CN长度的最大值为 +1 .
【解答】解:如图,取AB的中点D,连接DN,CD.
∵∠ABC=90°,AC=4,BC=2,
∴AB=,
∵∠ACB=90°,AD=BD,
∴CD=AB=,
∵AD=BD,MN=BN,
∴DN==1,
∴CN≤CD+DN,
∴CN≤,
∴CN的最大值为.
故答案为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学圆的“三大定理”
一.切割线定理
1.已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R= cm.
2.如图,在△ABC中,AB=AC,∠C=72°,⊙O过AB两点且与BC切于B,与AC交于D,连接BD,若BC=﹣1,则AC= .
3.如图,A,B,D,E四点在⊙O上,AE,BD的延长线相交于点C,直径AE为8,OC=12,∠EDC=∠BAO.
(1)求证:;
(2)计算CD CB的值,并指出CB的取值范围.
4.如图,⊙O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到P,过P作⊙O的切线,切点为C,若PC=2,求PD的长.
5.如图,PA是⊙O的切线,A为切点,PBC是过点O的割线.若PA=8cm,PB=4cm,则⊙O的直径为( )
A.6cm B.8cm C.12cm D.16cm
二.弦切角定理
6.如图,AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
7.如图PA切⊙O于点A,∠PAB=30°,则∠AOB= 度,∠ACB= 度.
8.如图,A、B为⊙O上的点,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D,若AC为∠BAD的平分线.
求证:(1)AB为⊙O的直径;(2)AC2=AB AD.
9.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于点C,AE⊥CE且交⊙O于点D.
求证:(1)DC=BC;
(2)BC2=AB DE.
10.如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于( )
A.40° B.50° C.60° D.70°
三.相交弦定理
11.如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,求AE的长.
12.已知如图,等腰△ABC内接于⊙O,∠B=∠ACB=30°,弦AD交BC于E,AE=2,ED=4,则⊙O的半径为 .
13.如图:若弦BC经过圆O的半径OA的中点P,且PB=3,PC=4,则圆O的直径为( )
A.7 B.8 C.9 D.10
14.如图,△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE的中点,如果BD∥CF,BC=2,则线段CD的长为 .
15.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP= .
四.圆的最值问题
16.如图,⊙O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是( )
A. B. C. D.
17.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,以A为圆心,2为半径作⊙A,M是⊙A上一动点,取线段BM的中点N,连接CN,则CN长度的最大值为 .
参考答案与试题解析
一.试题(共20小题)
1.已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R= cm.
【解答】解:∵PC是切线,
∴PC2=PA PB;
又∵PC=4,PA=3,
∴16=3(3+AB),
∴AB=,
∴半径R=.
2.如图,在△ABC中,AB=AC,∠C=72°,⊙O过AB两点且与BC切于B,与AC交于D,连接BD,若BC=﹣1,则AC= 2 .
【解答】解:∵AB=AC,∠C=72°,BC是⊙O的切线,
∴∠CBD=∠BAC=36°,
∴∠ABD=36°,
∴∠BDC=∠BCD=72°,
∴AD=BD=BC;
又∵BC是切线,
∴BC2=CD AC,
∴BC2=(AC﹣BC) AC(设AC=x),则可得到:(x﹣)2=,
解得:x1=2,x2=(x2<0不合题意,舍去).
∴AC=2.
3.如图,A,B,D,E四点在⊙O上,AE,BD的延长线相交于点C,直径AE为8,OC=12,∠EDC=∠BAO.
(1)求证:;
(2)计算CD CB的值,并指出CB的取值范围.
【解答】(1)证明:∵四边形ABDE内接于⊙O,
∴∠EDC=∠BAO,∠C=∠C,
∴△CDE∽△CAB,
∴;
(2)解:∵直径AE=8,OC=12,
∴AC=12+4=16,CE=12﹣4=8.
又∵=,
∴CD CB=AC CE=16×8=128.
连接OB,在△OBC中,OB=AE=4,OC=12,
故BC的范围是:8≤BC≤16.
4.如图,⊙O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到P,过P作⊙O的切线,切点为C,若PC=2,求PD的长.
【解答】解:(1)∵直径AB=10,弦DE⊥AB于点H,
∴DH=EH,
∴DH EH=AH BH=16,
∴DH=4,
∴DE=8;
(2)∵PC切⊙O于点C,
∴PC2=PD PE,
∵PC=2,
∴PD=2,或PD=﹣10(舍去),
∴PD=2.
5.如图,PA是⊙O的切线,A为切点,PBC是过点O的割线.若PA=8cm,PB=4cm,则⊙O的直径为( )
A.6cm B.8cm C.12cm D.16cm
【解答】解:∵PA2=PB PC,PA=8cm,PB=4cm,
∴PC=16cm,
∴BC=12cm.
故选:C.
6.如图,AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
【解答】解:∵AB是⊙O的直径,DE为⊙O的切线,∠CBE=40°,
∴∠A=∠CBE=40°.
故选:B.
7.如图PA切⊙O于点A,∠PAB=30°,则∠AOB= 60 度,∠ACB= 30 度.
【解答】解:由弦切角定理知,∠C=∠BAP=30°;
由圆周角定理知,∠AOB=2∠C=60°.
8.如图,A、B为⊙O上的点,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D,若AC为∠BAD的平分线.
求证:(1)AB为⊙O的直径;(2)AC2=AB AD.
【解答】证明:(1)连接BC,
AC平分∠BAD,
∴∠DAC=∠CAB.
又CD切⊙O于点C,
∴∠ACD=∠B(弦切角定理).
∵AD⊥CD,
∴∠ACD+∠DAC=90°.
即∠B+∠CAB=90°,∴∠BCA=90°.
∴AB是⊙O的直径(90°圆周角所对弦是直径).
(2)∵∠ACD=∠B,∠DAC=∠CAB,
∴△ACD∽△ABC.
∴.
∴AC2=AB AD.
9.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于点C,AE⊥CE且交⊙O于点D.
求证:(1)DC=BC;
(2)BC2=AB DE.
【解答】证明:(1)连接OC,
∵CE切圆O于点C,
∴∠ECO=90°,
∴∠E=∠ECO=90°,
∴AE∥CO,
∴∠DAC=∠ACO,
∴弧DC=弧BC,
∴DC=BC.
(2)∵弧DC=弧BC,CE切⊙O于C,
∴∠DCE=∠BAC.
又AB是⊙O直径,
∴∠CED=∠ACB=90°.
∴△DCE∽△BCA即=,而DC=BC.
∴BC2=AB DE.
10.如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于( )
A.40° B.50° C.60° D.70°
【解答】解:∵BD切⊙O于点B,
∴∠DBC=∠A=40°,
∵AB=AC,
∴∠ABC=∠C,
∴∠ABC=(180°﹣40°)÷2=70°.
故选:D.
11.如图,已知AB是⊙O的直径,弦CD⊥AB于E,CD=16cm,AB=20cm,求AE的长.
【解答】解:根据垂径定理可知CE=8cm,
根据相交弦定理可得:
64=BE×AE=(AB﹣AE)×AE
解方程得:AE=16(cm).
12.已知如图,等腰△ABC内接于⊙O,∠B=∠ACB=30°,弦AD交BC于E,AE=2,ED=4,则⊙O的半径为 2 .
【解答】解:连接OA,OC,AO交BC于点F,则OA=OC,∠B=∠C,
∴AB=AC,
由圆周角定理知,∠O=2∠D=60°,
所以等腰△OAC是等边三角形,
有AB=AC=OA,
∵∠B=∠C,
∴AE⊥BC
∵AB=AC,AE=AE,
∴Rt△ABE≌Rt△ACE,
∴BE=CE,∠AEB=∠AEC,
∵∠AEB+∠AEC=180°,
∴∠AEB=∠AEC=90°,
∴BF2=AB2﹣AF2,AF2+EF2=AE2,
由相交弦定理知,BE CE=AE ED=8,
而BE CE=(BF+EF)(BF﹣EF)=BF2﹣EF2=AB2﹣AF2﹣EF2=AB2﹣AE2=AB2﹣4=8,
∴AB2=12,
∴半径等于2.
13.如图:若弦BC经过圆O的半径OA的中点P,且PB=3,PC=4,则圆O的直径为( )
A.7 B.8 C.9 D.10
【解答】解:延长AO交⊙O于点D,
设⊙O的半径是x,
根据相交弦定理,得=12,x=4,
因此⊙O的直径是8.
故选:B.
14.如图,△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE的中点,如果BD∥CF,BC=2,则线段CD的长为 .
【解答】解:连接BF,
∵BD∥CF,
∴∠FCB=∠DBC.
∵AB=AC,
∴=,=,
∴∠BCD=∠DBC,AD是BC的垂直平分线,
∴四边形DCFB是菱形,
∴∠FCB=∠DCB,CE为等腰三角形FCD的顶角平分线.
设ED=x,则AE=5x,故x 5x=()2,
解得x=1,x=﹣1(舍去).
根据勾股定理得:CD==.
15.如图在⊙O中,弦AB、CD交于点P,如果CP=6,DP=3,AB=11,则AP= 2或9 .
【解答】解:根据相交弦定理,得:
AP PB=CP DP
∵AB=11
∴AP(11﹣AP)=CP DP
∴AP2﹣11AP+18=0
∴AP=2或9.
16.如图,⊙O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是( )
A. B. C. D.
【解答】解:如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO,AK.
由题意AB垂直平分线段OK,
∴AO=AK,
∵OA=OK,
∴OA=OK=AK,
∴∠OAK=∠AOK=60°.
∴AH=OA sin60°=4×=2,
∵OH⊥AB,
∴AH=BH,
∴AB=2AH=4,
∵OC+OH≥CT,
∴CT≤4+2=6,
∴CT的最大值为6,
∴△ABC的面积的最大值为××6=12,
故选:A.
17.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,以A为圆心,2为半径作⊙A,M是⊙A上一动点,取线段BM的中点N,连接CN,则CN长度的最大值为 +1 .
【解答】解:如图,取AB的中点D,连接DN,CD.
∵∠ABC=90°,AC=4,BC=2,
∴AB=,
∵∠ACB=90°,AD=BD,
∴CD=AB=,
∵AD=BD,MN=BN,
∴DN==1,
∴CN≤CD+DN,
∴CN≤,
∴CN的最大值为.
故答案为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
