北师大版2021-2022年初中数学八年级下册2.5一元一次不等式与一次函数课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学八年级下册2.5一元一次不等式与一次函数课堂练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 447.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 00:11:38 | ||
图片预览



文档简介
2021-2022年初中数学八年级下册同步(北师大版)
2.5一元一次不等式与一次函数-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是一次函数的图象,若,则x的取值范围是( )
A. B. C. D.
2.已知一次函数y=kx+b的图像,如图所示,当x<0时,y的取值范围是( )
A.y>0 B.y<0 C.-2<y<0 D.y<-2
3.一元一次方程的解是,函数的图象与x轴的交点坐标为( )
A. B. C. D.
4.如图所示,函数和的图像相交于,两点,当时,的取值范围是( )
A. B. C.或 D.
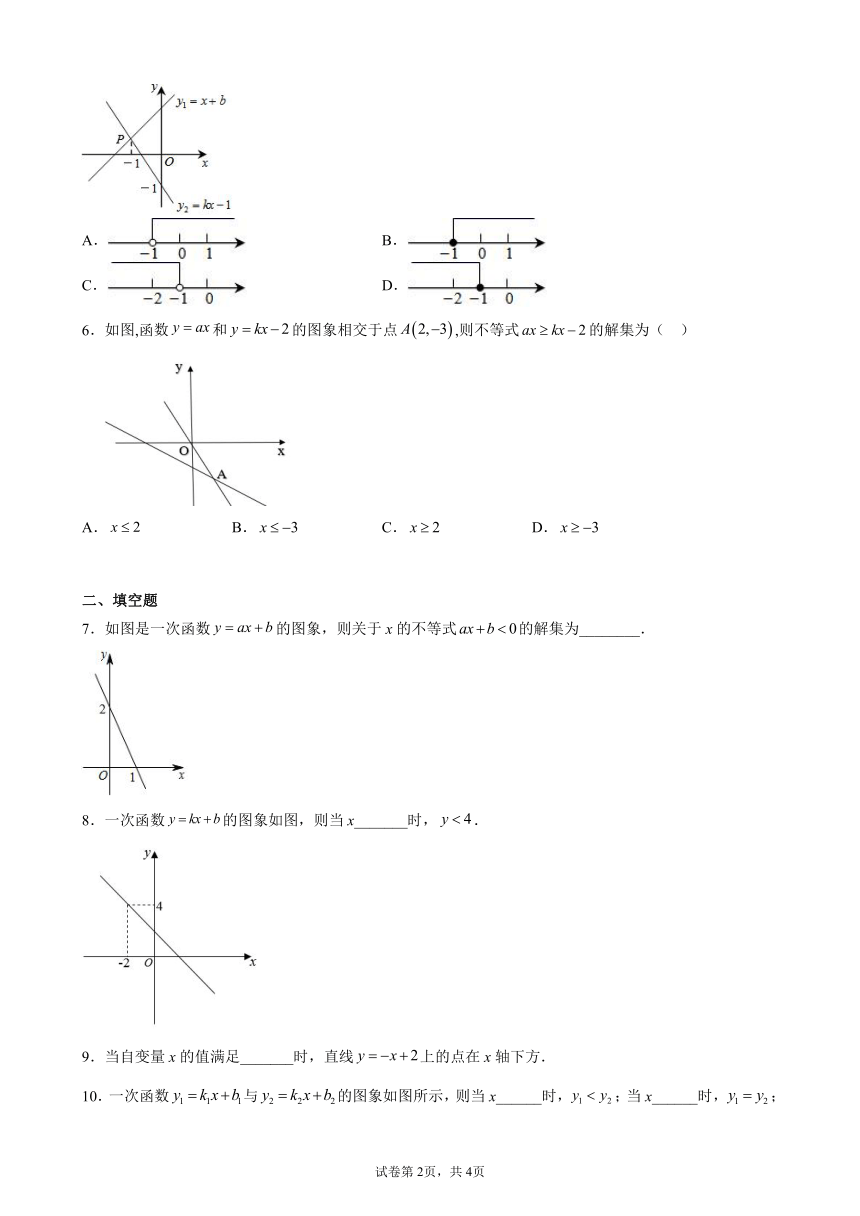
5.如图,直线与相交于点P,点P的横坐标为-1,则关于x的不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.如图,函数和的图象相交于点,则不等式的解集为( )
A. B. C. D.
二、填空题
7.如图是一次函数的图象,则关于x的不等式的解集为________.
8.一次函数的图象如图,则当x_______时,.
9.当自变量x的值满足_______时,直线上的点在x轴下方.
10.一次函数与的图象如图所示,则当x______时,;当x______时,;当x______时,.
11.已知直线与相交于点,则不等式的解集是________.
12.如图,直线与直线均经过点,则不等式的解集为______.
三、解答题
13.试根据函数的性质或图象,确定x取何值时:
(1); (2).
14.已知,,当取哪些值时,?你是怎样做的?与同伴交流.
15.已知函数和相交于点.
(1)求k、b的值;
(2)在同一坐标系中画出两个函数的图象,利用图象求当x取何值时有:①;②且.
16.已知一次函数;
(1)画出函数的图象;
(2)当x为何值时,?
(3)当时,求y的变化范围,并指出当x为何值时,y有最大值?
17.如图,平面直角坐标系中画出了函数的图象.
(1)根据图象求k,b的值;
(2)在图中画出的图象;
(3)当x______时,函数的函数值大于函数的函数值.
18.如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是 ;
(2)关于x的不等式mx+n<1的解集是 ;
(3)当x满足 的条件时,y1 y2;
(4)当x满足 的条件时,0试卷第4页,共4页
试卷第3页,共4页
参考答案
1.C
【解析】解:如图,由函数图像可知:一次函数图像与x轴交点为(-3,0),当x>-3时,一次函数图像在x轴的上方,
∴当x>-3,y>0,
故选C.
2.D
【解析】通过观察图象得到x<0时,图象在y轴的左边,即可得到对应的y的取值范围.
当x<0时,图象在y轴的左边,
所以对应的y的取值范围为y<-2,
故选D.
3.A
【解析】一元一次方程的解是,
当时,,
故函数的图象与x轴的交点坐标为.
故选A.
4.C
【解析】解:∵当x≥0时,y1=x;当x<0时,y1= x, 两直线的交点为(2,2),( 1,1),
∴由图象可知:当y1>y2时x的取值范围为:x< 1或x>2.
故选C.
5.C
【解析】由图像可知当x<-1时,,
∴可在数轴上表示为:
故选C.
6.A
【解析】因为点A的坐标为,
看函数图象,当的图象在的图像上方时,,此时
故选:A.
7.
【解析】解:根据图象得:当 时,函数图象位于 轴下方,此时 ,
∴关于x的不等式的解集为.
故答案为:.
8.
【解析】解:观察函数图象,当时,
故答案为.
9.
【解析】当直线上的点在x轴下方,
则y < 0,
-x+2<0,
解得:x>2,
即当自变量x的值满足x > 2时,
直线上的点在x轴下方,
故答案为:.
10.
【解析】解:∵一次函数与的图象的交点坐标为(1,-3),在交点的右侧一次函数的图象在一次函数的图象的下方即
∴x>1,
当x>1时,;
一次函数的图象与一次函数的图象相交时,即,
∴x=1,
当x=1时,:
在交点的左侧,一次函数的图象在一次函数的图象的上方即
∴x<1,
当x<1时,;
故答案为;;.
11.
【解析】解:已知直线y=x 2与y= x+2相交于点(2,0),直线y=x 2中y随x的增大而增大,而y= x+2中y随x的增大而减小
因而不等式x 2≥ x+2的解集是:x≥2
故答案为:x≥2.
12.
【解析】将点代入中得,
观察图象可知,在时,直线的图象在直线图象的上方,
不等式的解集为:,
故答案为:.
13.(1);(2).
【解析】解:∵
∴一次函数与x轴的交点坐标为,与y轴的交点坐标为,作图如下:
(1)如图,当时,;
(2)如图,当时,
14.,见解析.
【解析】解:∵,,,
∴,
∴,
解得.
15.(1),;(2)画图见解析,①,②
【解析】解:(1)将点代入函数得,解得
将点代入函数得,解得
故答案为,
(2)列表,如下
0 2
-2 -1
5 -1
函数图像如下:
①由图像可得:当时,,故答案为
②将代入得,,由图像可知时,
将代入得,,由图像可知时,
由此可得
16.(1)见解析;(2);(3),当时,y取最大值7
【解析】解:(1)∵一次函数y=﹣2x+3的图象是一条直线,
当x=0时,解得y=3;当y=0时,解得x=,
∴直线与坐标轴的两个交点分别是(0,3)和(,0),
其图象如下:
(2)由题意得,,解得,
当x<时,.
(3)∵y=﹣2x+3,
∴用含y的式子表示x得:,
又∵﹣2≤x≤3,
∴,
解得:﹣3≤y≤7.
∵-2<0,
∴当时,y取最大值7.
17.(1);(2)图象见解析;(3).
【解析】解:(1)把(﹣2,0),(0,2)代入解析式y=kx+b得,解得,k=1,b=2;
(2)当x=0时,y=2,当y=0时,0=﹣2x+2,解得,x=1,经过(0,2)和(1,0)画一条直线,就是的图象,如图所示;
(3)根据题意可列不等式,x+2>﹣2x+2,解得x>0,
故答案为:>0.
18.(1);(2);(3);(4).
【解析】(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时, y2>0,即不等式ax+b>0的解集是x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时, y1<1,即不等式mx+n<1的解集是x<0;
(3)由一次函数的图象知,两条直线的交点坐标是(2,1.8),当函数y1的图象在y2的下面时,有x 2,
∴当x≤2时, y1≤ y2;
(4)如图所示,当2故答案为:(1);(2);(3);(4).
答案第6页,共6页
答案第5页,共6页
2.5一元一次不等式与一次函数-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是一次函数的图象,若,则x的取值范围是( )
A. B. C. D.
2.已知一次函数y=kx+b的图像,如图所示,当x<0时,y的取值范围是( )
A.y>0 B.y<0 C.-2<y<0 D.y<-2
3.一元一次方程的解是,函数的图象与x轴的交点坐标为( )
A. B. C. D.
4.如图所示,函数和的图像相交于,两点,当时,的取值范围是( )
A. B. C.或 D.
5.如图,直线与相交于点P,点P的横坐标为-1,则关于x的不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.如图,函数和的图象相交于点,则不等式的解集为( )
A. B. C. D.
二、填空题
7.如图是一次函数的图象,则关于x的不等式的解集为________.
8.一次函数的图象如图,则当x_______时,.
9.当自变量x的值满足_______时,直线上的点在x轴下方.
10.一次函数与的图象如图所示,则当x______时,;当x______时,;当x______时,.
11.已知直线与相交于点,则不等式的解集是________.
12.如图,直线与直线均经过点,则不等式的解集为______.
三、解答题
13.试根据函数的性质或图象,确定x取何值时:
(1); (2).
14.已知,,当取哪些值时,?你是怎样做的?与同伴交流.
15.已知函数和相交于点.
(1)求k、b的值;
(2)在同一坐标系中画出两个函数的图象,利用图象求当x取何值时有:①;②且.
16.已知一次函数;
(1)画出函数的图象;
(2)当x为何值时,?
(3)当时,求y的变化范围,并指出当x为何值时,y有最大值?
17.如图,平面直角坐标系中画出了函数的图象.
(1)根据图象求k,b的值;
(2)在图中画出的图象;
(3)当x______时,函数的函数值大于函数的函数值.
18.如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是 ;
(2)关于x的不等式mx+n<1的解集是 ;
(3)当x满足 的条件时,y1 y2;
(4)当x满足 的条件时,0
试卷第3页,共4页
参考答案
1.C
【解析】解:如图,由函数图像可知:一次函数图像与x轴交点为(-3,0),当x>-3时,一次函数图像在x轴的上方,
∴当x>-3,y>0,
故选C.
2.D
【解析】通过观察图象得到x<0时,图象在y轴的左边,即可得到对应的y的取值范围.
当x<0时,图象在y轴的左边,
所以对应的y的取值范围为y<-2,
故选D.
3.A
【解析】一元一次方程的解是,
当时,,
故函数的图象与x轴的交点坐标为.
故选A.
4.C
【解析】解:∵当x≥0时,y1=x;当x<0时,y1= x, 两直线的交点为(2,2),( 1,1),
∴由图象可知:当y1>y2时x的取值范围为:x< 1或x>2.
故选C.
5.C
【解析】由图像可知当x<-1时,,
∴可在数轴上表示为:
故选C.
6.A
【解析】因为点A的坐标为,
看函数图象,当的图象在的图像上方时,,此时
故选:A.
7.
【解析】解:根据图象得:当 时,函数图象位于 轴下方,此时 ,
∴关于x的不等式的解集为.
故答案为:.
8.
【解析】解:观察函数图象,当时,
故答案为.
9.
【解析】当直线上的点在x轴下方,
则y < 0,
-x+2<0,
解得:x>2,
即当自变量x的值满足x > 2时,
直线上的点在x轴下方,
故答案为:.
10.
【解析】解:∵一次函数与的图象的交点坐标为(1,-3),在交点的右侧一次函数的图象在一次函数的图象的下方即
∴x>1,
当x>1时,;
一次函数的图象与一次函数的图象相交时,即,
∴x=1,
当x=1时,:
在交点的左侧,一次函数的图象在一次函数的图象的上方即
∴x<1,
当x<1时,;
故答案为;;.
11.
【解析】解:已知直线y=x 2与y= x+2相交于点(2,0),直线y=x 2中y随x的增大而增大,而y= x+2中y随x的增大而减小
因而不等式x 2≥ x+2的解集是:x≥2
故答案为:x≥2.
12.
【解析】将点代入中得,
观察图象可知,在时,直线的图象在直线图象的上方,
不等式的解集为:,
故答案为:.
13.(1);(2).
【解析】解:∵
∴一次函数与x轴的交点坐标为,与y轴的交点坐标为,作图如下:
(1)如图,当时,;
(2)如图,当时,
14.,见解析.
【解析】解:∵,,,
∴,
∴,
解得.
15.(1),;(2)画图见解析,①,②
【解析】解:(1)将点代入函数得,解得
将点代入函数得,解得
故答案为,
(2)列表,如下
0 2
-2 -1
5 -1
函数图像如下:
①由图像可得:当时,,故答案为
②将代入得,,由图像可知时,
将代入得,,由图像可知时,
由此可得
16.(1)见解析;(2);(3),当时,y取最大值7
【解析】解:(1)∵一次函数y=﹣2x+3的图象是一条直线,
当x=0时,解得y=3;当y=0时,解得x=,
∴直线与坐标轴的两个交点分别是(0,3)和(,0),
其图象如下:
(2)由题意得,,解得,
当x<时,.
(3)∵y=﹣2x+3,
∴用含y的式子表示x得:,
又∵﹣2≤x≤3,
∴,
解得:﹣3≤y≤7.
∵-2<0,
∴当时,y取最大值7.
17.(1);(2)图象见解析;(3).
【解析】解:(1)把(﹣2,0),(0,2)代入解析式y=kx+b得,解得,k=1,b=2;
(2)当x=0时,y=2,当y=0时,0=﹣2x+2,解得,x=1,经过(0,2)和(1,0)画一条直线,就是的图象,如图所示;
(3)根据题意可列不等式,x+2>﹣2x+2,解得x>0,
故答案为:>0.
18.(1);(2);(3);(4).
【解析】(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时, y2>0,即不等式ax+b>0的解集是x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时, y1<1,即不等式mx+n<1的解集是x<0;
(3)由一次函数的图象知,两条直线的交点坐标是(2,1.8),当函数y1的图象在y2的下面时,有x 2,
∴当x≤2时, y1≤ y2;
(4)如图所示,当2
答案第6页,共6页
答案第5页,共6页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
