北师大版2021-2022年初中数学八年级下册1.4角平分线课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学八年级下册1.4角平分线课堂练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 00:19:12 | ||
图片预览




文档简介
2021-2022年初中数学八年级下册同步(北师大版)
1.4角平分线-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.AD是△BAC的角平分线,过D向AB、AC两边作垂线,垂足为E、F,则下列错误的是( )
A.DE=DF B.AE=AF C.BD=CD D.∠ADE=∠ADF
2.射线OC在∠AOB的内部,下列给出的条件中不能得出OC是∠AOB的平分线的是( )
A.∠AOC=∠BOC
B.∠AOC+∠BOC=∠AOB
C.∠AOB=2∠AOC
D.∠BOC=∠AOB
3.到△ABC的三边距离相等的点是△ABC的( )
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点
4.如图,,若,则的度数为( )
A. B. C. D.
5.如图, AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.6 B.5 C.4 D.3
6.利用作角平分线的方法,可以把一个已知角( )
A.三等分 B.四等分 C.五等分 D.六等分
二、填空题
7.如图,△ABC中,AD平分∠BAC,CD⊥AD,若∠ABC与∠ACD互补,CD=8,则BC的长为_____________.
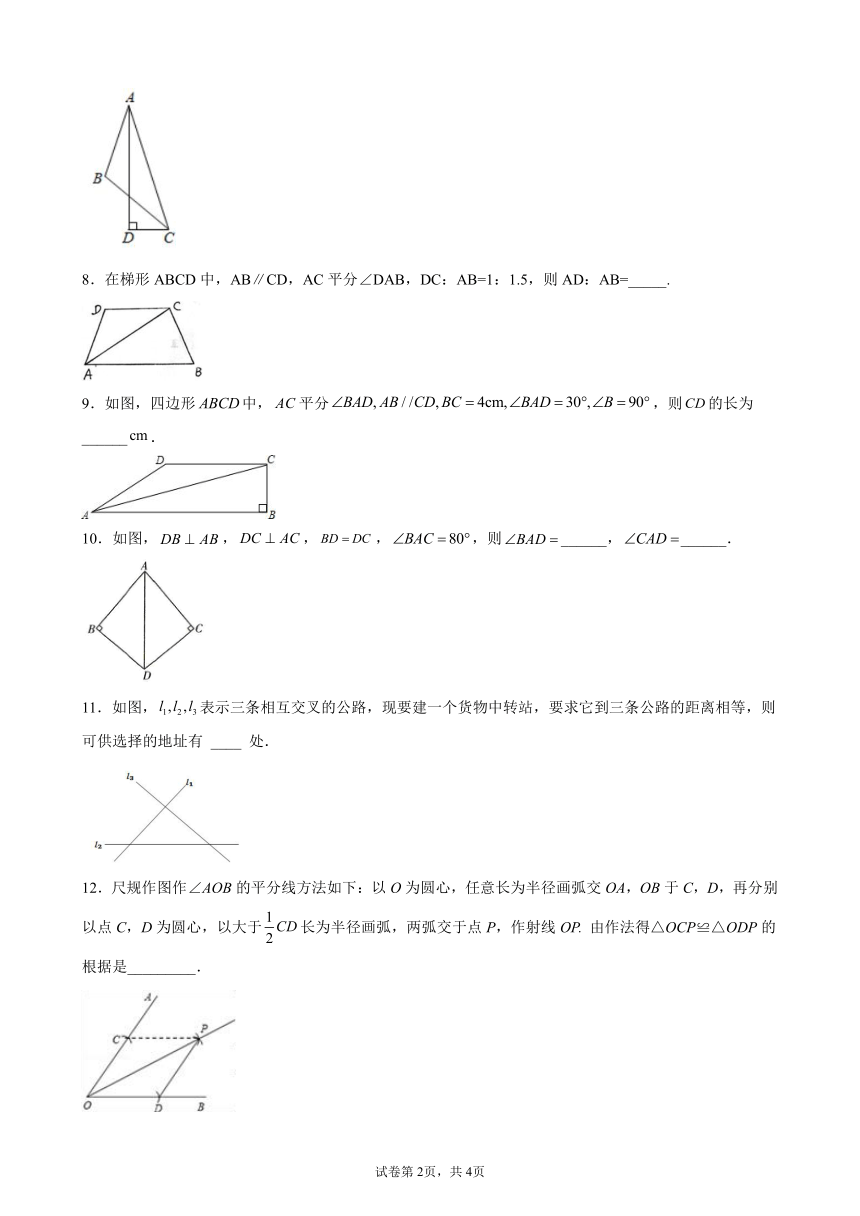
8.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
9.如图,四边形中,平分,则的长为______.
10.如图,,,,,则______,______.
11.如图,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 ____ 处.
12.尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP. 由作法得△OCP≌△ODP的根据是_________.
三、解答题
13.已知:如图,,.求证:BD平分.
14.如图,在中,,AD平分,于点F,,求证:.
15.已知:如图,是的角平分线.
求证:.
16.如图,在中,,点D在上,,,,垂足分别为E,F,且,求的长.
17.如图,某市有两个粮食市场C、D,附近有两条交叉的公路.现计划修建一座大型粮仓P,为了运输方便,希望该粮仓到两条公路的距离相等,且到两个粮食市场C、D的距离也相等,请在图中设计出该粮仓的位置.(尺规作图,不写作法,写清结论.)
18.如图,三条公路两两相交,现计划修建一个油库.
(1)如果要求油库到两条公路的距离都相等,那么如何选择油库的位置?
(2)如果要求油库到这三条公路的距离都相等,那么如何选择油库的位置?
试卷第4页,共4页
试卷第3页,共4页
参考答案
1.C
【解析】解:如图,∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,故A选项错误,
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,故B、D选项错误,
只有△ABC是等腰三角形时,BD=CD,故C选项正确.
故选C.
2.B
【解析】解:当OC是∠AOB的平分线时,∠AOC=∠BOC,∠AOB=2∠AOC,,所以A、C、D选项能判断OC是∠AOB的平分线.
∠AOB=∠AOC+∠BOC只能说明射线OC在∠AOB内,不一定是角平分线.
故选B.
3.B
【解析】解:设这个点为点P,
∵点P到AB、AC两边的距离相等,
∴点P在∠BAC的平分线上,
同理可得点P在∠ABC、∠ACB的平分线上,
∴点P为三个内角的角平分线的交点,
故选:B.
4.C
【解析】∵,
∴平分,
∵,
∴,
∴,
故选:C.
5.D
【解析】解:过D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,
∴DE=DF=2,
∵S△ABC=7,
∴S△ADB+S△ADC=7,
∴×AB×DE+×AC×DF=7,
∴×4×2+×AC×2=7,
解得:AC=3.
故选D .
6.B
【解析】利用作角平分线的方法,可以把一个已知角二等分,进而可以将两角再次等分,故可以把一个已知角四等分.
故选:B.
7.16
【解析】解:延长AB交CD的延长线于点E,如图所示:
∵AD平分∠BAC,CD⊥AD,
∴∠EAD=∠CAD,∠ADE=∠ADC=90°,
∵AD=AD,
∴△ADE≌△ADC,
∴∠E=∠ACD,ED=DC,
又∵∠ABC+∠ACD=180°,∠ABC+∠EBC=180°,
∴∠E=∠ACD=∠EBC,
∴BC=EC=2DC,
∵DC=8,
∴BC=EC=16;
故答案为16.
8.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD =∠DCA
∴AD = CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
9.8
【解析】解:过C作CE∥AD于E,
∴∠DAC=∠ECA,∠DAB=∠CEB=30°,
∵CD∥AB,
∴∠DCA=∠EAC,
∵AC平分∠DAB,
∴∠DAC=∠BAC
∴∠DAC=∠BAC =∠DCA=∠ECA,
在△ADC和△AEC中,
∴△ADC≌△AEC(ASA),
∴DC=EC,
∵∠CEB=30°,∠AED=90°,
∴CE=2BC=2×4cm=8cm,
∴CD=CE=8cm.
故答案为8.
10.
【解析】解:∵,,,
∴AD为∠BAC的角平分线,
∴,
故答案为:;.
11.4.
【解析】解:如图示,作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
故答案是:4.
12.SSS
【解析】解:∵以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD.以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP.在△OCP和△ODP中,∵OC=OD,OP=OP,CP=DP,∴△OCP≌△ODP(SSS).故答案为SSS.
13.证明见解析.
【解析】解:∵(已知),
∴(两直线平行,内错角相等).
又∵(已知),
∴(等量代换).
∴BD平分(角平分线的定义).
14.证明见解析
【解析】证明:∵在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,
∴DE=DF,∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
15.证明见解析
【解析】证明:如图,过点D作DE⊥AB于点E,
∵AD平分,DE⊥AB,,
∴DE=DC,
∵在直角三角形BED中,,
∴,
∴.
16.5
【解析】解:∵DE⊥AB,DF⊥AC,DE=DF,
∴,
在Rt△ADE中,∠BAD=30°,
∴DE.
17.答案见解析
【解析】
18.(1)油库的位置在直线MN或直线EF上;(2)见解析
【解析】解:(1)如图,油库的位置在直线MN或直线EF上;
(2)如图,点P1,P2,P3,P4即为所求.
答案第6页,共6页
答案第7页,共1页
1.4角平分线-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.AD是△BAC的角平分线,过D向AB、AC两边作垂线,垂足为E、F,则下列错误的是( )
A.DE=DF B.AE=AF C.BD=CD D.∠ADE=∠ADF
2.射线OC在∠AOB的内部,下列给出的条件中不能得出OC是∠AOB的平分线的是( )
A.∠AOC=∠BOC
B.∠AOC+∠BOC=∠AOB
C.∠AOB=2∠AOC
D.∠BOC=∠AOB
3.到△ABC的三边距离相等的点是△ABC的( )
A.三边中线的交点 B.三条角平分线的交点 C.三边上高的交点 D.三边垂直平分线的交点
4.如图,,若,则的度数为( )
A. B. C. D.
5.如图, AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.6 B.5 C.4 D.3
6.利用作角平分线的方法,可以把一个已知角( )
A.三等分 B.四等分 C.五等分 D.六等分
二、填空题
7.如图,△ABC中,AD平分∠BAC,CD⊥AD,若∠ABC与∠ACD互补,CD=8,则BC的长为_____________.
8.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
9.如图,四边形中,平分,则的长为______.
10.如图,,,,,则______,______.
11.如图,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 ____ 处.
12.尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP. 由作法得△OCP≌△ODP的根据是_________.
三、解答题
13.已知:如图,,.求证:BD平分.
14.如图,在中,,AD平分,于点F,,求证:.
15.已知:如图,是的角平分线.
求证:.
16.如图,在中,,点D在上,,,,垂足分别为E,F,且,求的长.
17.如图,某市有两个粮食市场C、D,附近有两条交叉的公路.现计划修建一座大型粮仓P,为了运输方便,希望该粮仓到两条公路的距离相等,且到两个粮食市场C、D的距离也相等,请在图中设计出该粮仓的位置.(尺规作图,不写作法,写清结论.)
18.如图,三条公路两两相交,现计划修建一个油库.
(1)如果要求油库到两条公路的距离都相等,那么如何选择油库的位置?
(2)如果要求油库到这三条公路的距离都相等,那么如何选择油库的位置?
试卷第4页,共4页
试卷第3页,共4页
参考答案
1.C
【解析】解:如图,∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,故A选项错误,
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,故B、D选项错误,
只有△ABC是等腰三角形时,BD=CD,故C选项正确.
故选C.
2.B
【解析】解:当OC是∠AOB的平分线时,∠AOC=∠BOC,∠AOB=2∠AOC,,所以A、C、D选项能判断OC是∠AOB的平分线.
∠AOB=∠AOC+∠BOC只能说明射线OC在∠AOB内,不一定是角平分线.
故选B.
3.B
【解析】解:设这个点为点P,
∵点P到AB、AC两边的距离相等,
∴点P在∠BAC的平分线上,
同理可得点P在∠ABC、∠ACB的平分线上,
∴点P为三个内角的角平分线的交点,
故选:B.
4.C
【解析】∵,
∴平分,
∵,
∴,
∴,
故选:C.
5.D
【解析】解:过D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,
∴DE=DF=2,
∵S△ABC=7,
∴S△ADB+S△ADC=7,
∴×AB×DE+×AC×DF=7,
∴×4×2+×AC×2=7,
解得:AC=3.
故选D .
6.B
【解析】利用作角平分线的方法,可以把一个已知角二等分,进而可以将两角再次等分,故可以把一个已知角四等分.
故选:B.
7.16
【解析】解:延长AB交CD的延长线于点E,如图所示:
∵AD平分∠BAC,CD⊥AD,
∴∠EAD=∠CAD,∠ADE=∠ADC=90°,
∵AD=AD,
∴△ADE≌△ADC,
∴∠E=∠ACD,ED=DC,
又∵∠ABC+∠ACD=180°,∠ABC+∠EBC=180°,
∴∠E=∠ACD=∠EBC,
∴BC=EC=2DC,
∵DC=8,
∴BC=EC=16;
故答案为16.
8.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD =∠DCA
∴AD = CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
9.8
【解析】解:过C作CE∥AD于E,
∴∠DAC=∠ECA,∠DAB=∠CEB=30°,
∵CD∥AB,
∴∠DCA=∠EAC,
∵AC平分∠DAB,
∴∠DAC=∠BAC
∴∠DAC=∠BAC =∠DCA=∠ECA,
在△ADC和△AEC中,
∴△ADC≌△AEC(ASA),
∴DC=EC,
∵∠CEB=30°,∠AED=90°,
∴CE=2BC=2×4cm=8cm,
∴CD=CE=8cm.
故答案为8.
10.
【解析】解:∵,,,
∴AD为∠BAC的角平分线,
∴,
故答案为:;.
11.4.
【解析】解:如图示,作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
故答案是:4.
12.SSS
【解析】解:∵以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD.以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP.在△OCP和△ODP中,∵OC=OD,OP=OP,CP=DP,∴△OCP≌△ODP(SSS).故答案为SSS.
13.证明见解析.
【解析】解:∵(已知),
∴(两直线平行,内错角相等).
又∵(已知),
∴(等量代换).
∴BD平分(角平分线的定义).
14.证明见解析
【解析】证明:∵在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,
∴DE=DF,∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
15.证明见解析
【解析】证明:如图,过点D作DE⊥AB于点E,
∵AD平分,DE⊥AB,,
∴DE=DC,
∵在直角三角形BED中,,
∴,
∴.
16.5
【解析】解:∵DE⊥AB,DF⊥AC,DE=DF,
∴,
在Rt△ADE中,∠BAD=30°,
∴DE.
17.答案见解析
【解析】
18.(1)油库的位置在直线MN或直线EF上;(2)见解析
【解析】解:(1)如图,油库的位置在直线MN或直线EF上;
(2)如图,点P1,P2,P3,P4即为所求.
答案第6页,共6页
答案第7页,共1页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
