北师大版2021-2022年初中数学八年级下册1.3线段的垂直平分线课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学八年级下册1.3线段的垂直平分线课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 589.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 00:00:00 | ||
图片预览


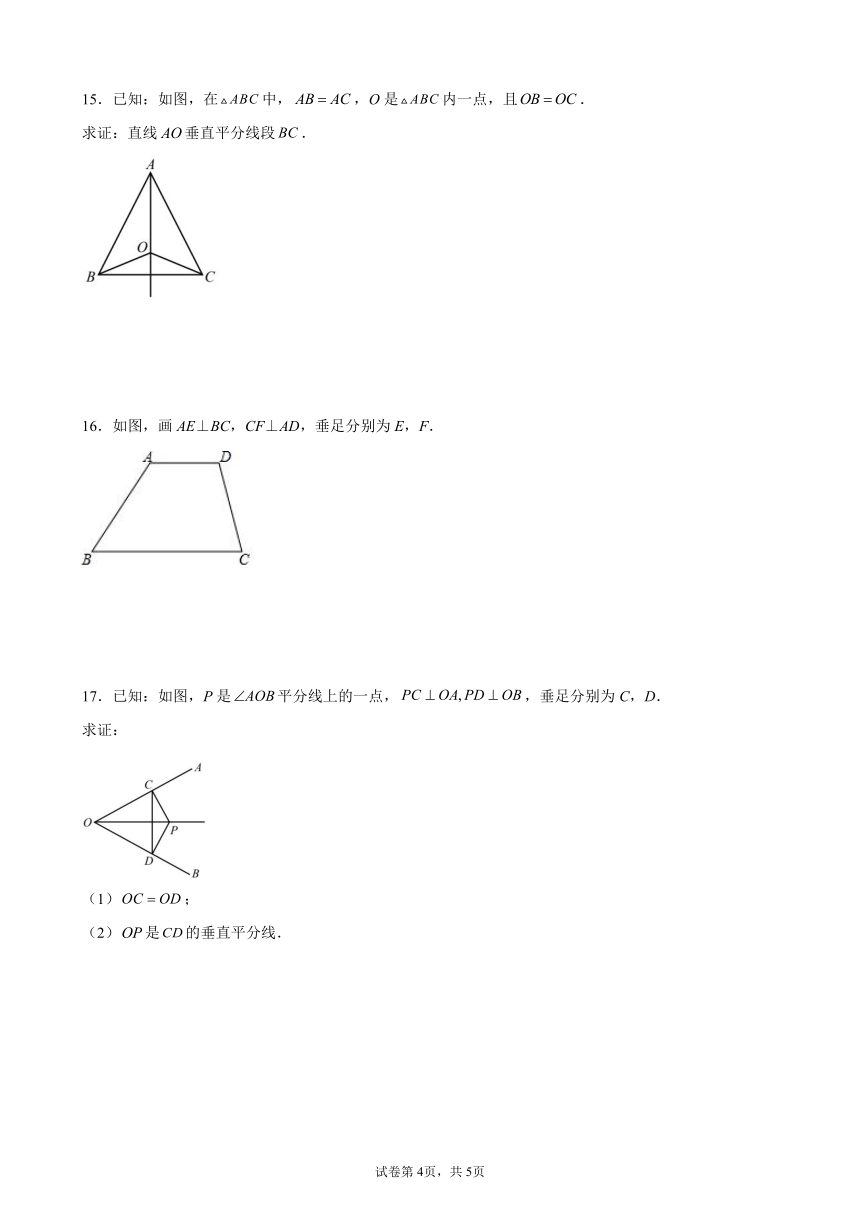

文档简介
2021-2022年初中数学八年级下册同步(北师大版)
1.3线段的垂直平分线-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.到三角形三个顶点距离相等的点是此三角形( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边中垂线的交点
2.如图,DE是△ABC中AC边上的垂直平分线,如果BC=8cm,AB=10cm,则△EBC的周长为( )
A.16cm B.18cm C.26cm D.28cm
3.如图,已知,则下列说法中不一定正确的是( )
A. B. C. D.
4.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
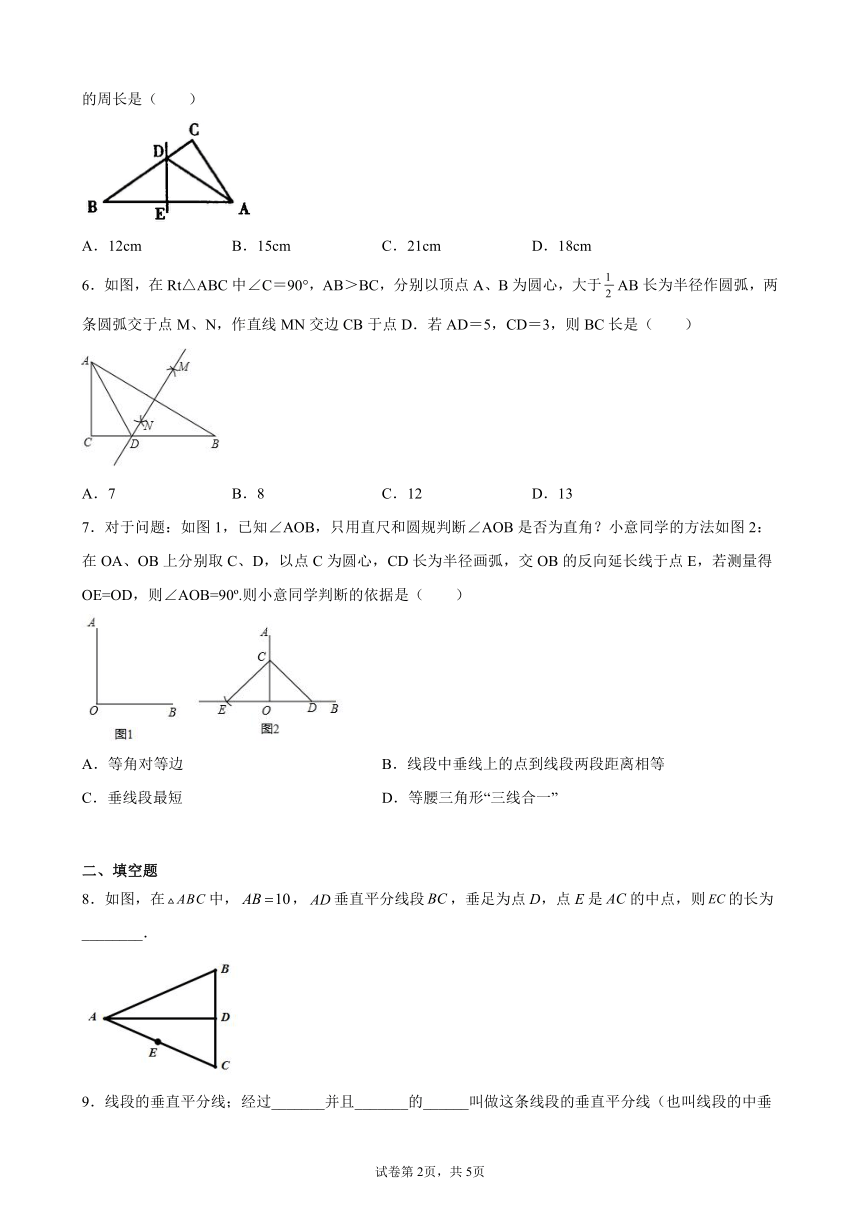
5.如图,中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,的周长为9cm,则的周长是( )
A.12cm B.15cm C.21cm D.18cm
6.如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于点D.若AD=5,CD=3,则BC长是( )
A.7 B.8 C.12 D.13
7.对于问题:如图1,已知∠AOB,只用直尺和圆规判断∠AOB是否为直角?小意同学的方法如图2:在OA、OB上分别取C、D,以点C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若测量得OE=OD,则∠AOB=90 .则小意同学判断的依据是( )
A.等角对等边 B.线段中垂线上的点到线段两段距离相等
C.垂线段最短 D.等腰三角形“三线合一”
二、填空题
8.如图,在中,,垂直平分线段,垂足为点D,点E是的中点,则的长为________.
9.线段的垂直平分线;经过_______并且_______的______叫做这条线段的垂直平分线(也叫线段的中垂线).
10.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
11.已知线段AB及一点P,PA=PB=3cm,则点P在__________上.
12.△ABC中,若AB﹣AC=2cm,BC的垂直平分线交AB于D点,且△ACD的周长为14cm,则AB=_____,AC=_____.
三、解答题
13.如图,A,B表示两个仓库,要在A,B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
14.已知:如图,是线段的垂直平分线,E,F是上的两点.
求证:.
15.已知:如图,在中,,O是内一点,且.
求证:直线垂直平分线段.
16.如图,画AE⊥BC,CF⊥AD,垂足分别为E,F.
17.已知:如图,P是平分线上的一点,,垂足分别为C,D.
求证:
(1);
(2)是的垂直平分线.
18.为筹办一个大型运动会,某市政府打算修建一个大型体育中心.在选址过程中,有人建议该体育中心所在位置应与该市的三个城镇中心(图中以P,Q,R表示)的距离相等.
(1)根据上述建议,试在图(1)中画出体育中心G的位置;
(2)如果这三个城镇的位置如图(2)所示,是一个钝角,那么根据上述建议,体育中心G应在什么位置?
(3)你对上述建议有何评论?你对选址有什么建议?
试卷第4页,共5页
试卷第5页,共5页
参考答案
1.D
【解析】解:∵垂直平分线上任意一点,到线段两端点的距离相等,
∴到三角形三个顶点的距离相等的点是三角形三边中垂线的交点.
故选:D.
2.B
【解析】解:∵DE是△ABC中AC边上的垂直平分线,
∴AE=CE,
∵BC=8cm,AB=10cm,
∴△EBC的周长为:BC+BE+CE=BC+BE+AE=BC+AB=8+10=18(cm).
故选:B.
3.A
【解析】解:∵,
∴垂直平分线段,
∴,,,
故正确,不符合题意;
∴只有选项A不一定正确,符合题意.
故选:
4.B
【解析】根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
5.B
【解析】解:由DE是边AB的垂直平分线,
∴AD=BD,AE=BE,
由△ADC的周长为9cm,
∴AC+BC=9,
∵AE=3,
∴AB=6,
∴△ABC的周长是15cm,
故选:B.
6.B
【解析】解:∵顶点A、B为圆心,大于AB长为半径作圆弧
∴MN为AB的垂直平分线
∴AD=BD=5
∵BC=BD+CD
∴BC=AD+CD=5+3=8
故选B.
7.B
【解析】解:根据题意,
∵CD=CE,OE=OD,
∴AO是线段DE的垂直平分线,
∴∠AOB=90°;
则小意同学判断的依据是:线段中垂线上的点到线段两段距离相等;
故选:B.
8.5
【解析】∵垂直平分,,
∴,
∵点E是的中点,
∴.
故答案为:5.
9.线段的中点 垂直于这条线段 直线
【解析】解:经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
故填:线段的中点,垂直于这条线段,直线.
10.垂直
【解析】解:如图,连接、,
∵,
∴点A在线段的垂直平分线上,点D在线段的垂直平分线上,
∴根据两点确定一条直线得出直线是线段的垂直平分线,
故答案为:垂直.
11.线段AB的垂直平分线
【解析】因为PA=PB=3cm,
所以P点一定在线段AB的垂直平分线上.
故答案为:线段AB的垂直平分线.
12.AB=8cm AC=6cm
【解析】根据线段垂直平分线性质求出BD=DC,根据三角形周长AD+BD+AC=AB+AC=14cm,根据已知得出AC=AB-2cm,即可求出AC=6cm,AB=8cm.
故答案为8,6.
13.见解析.
【解析】解:连接AB,分别以A和B为圆心,以大于为半径的两弧交于点E和F,
作直线EF,与河岸交于点C,如图,则码头应建在点C处.
14.证明见解析
【解析】证明:是线段的垂直平分线,E,F是上的两点,
,
又,
(SSS),
.
15.证明见解析
【解析】证明:,,
,
是的垂直平分线.
即直线垂直平分线段.
16.见解析
【解析】解:如图,AE、CF为所作.
.
17.(1)证明见解析;(2)证明见解析.
【解析】解:(1)证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD;
(2)证明:∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP
∵由(1)知,OC=OD,
∴在△COE与△DOE中,
,
∴△COE≌△DOE,
∴CE=DE,OE⊥CD,即OP是CD的垂直平分线.
18.(1)见解析;(2)见解析;(3)见解析.
【解析】解:(1)如图,点G即为所求;
(2)如图,点G即为所求;
(3)上述建议非常合理,选址可以选在到该市的三个城镇中心的距离相等的位置.
答案第6页,共1页
答案第5页,共5页
1.3线段的垂直平分线-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.到三角形三个顶点距离相等的点是此三角形( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高的交点 D.三边中垂线的交点
2.如图,DE是△ABC中AC边上的垂直平分线,如果BC=8cm,AB=10cm,则△EBC的周长为( )
A.16cm B.18cm C.26cm D.28cm
3.如图,已知,则下列说法中不一定正确的是( )
A. B. C. D.
4.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
5.如图,中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,的周长为9cm,则的周长是( )
A.12cm B.15cm C.21cm D.18cm
6.如图,在Rt△ABC中∠C=90°,AB>BC,分别以顶点A、B为圆心,大于AB长为半径作圆弧,两条圆弧交于点M、N,作直线MN交边CB于点D.若AD=5,CD=3,则BC长是( )
A.7 B.8 C.12 D.13
7.对于问题:如图1,已知∠AOB,只用直尺和圆规判断∠AOB是否为直角?小意同学的方法如图2:在OA、OB上分别取C、D,以点C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若测量得OE=OD,则∠AOB=90 .则小意同学判断的依据是( )
A.等角对等边 B.线段中垂线上的点到线段两段距离相等
C.垂线段最短 D.等腰三角形“三线合一”
二、填空题
8.如图,在中,,垂直平分线段,垂足为点D,点E是的中点,则的长为________.
9.线段的垂直平分线;经过_______并且_______的______叫做这条线段的垂直平分线(也叫线段的中垂线).
10.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
11.已知线段AB及一点P,PA=PB=3cm,则点P在__________上.
12.△ABC中,若AB﹣AC=2cm,BC的垂直平分线交AB于D点,且△ACD的周长为14cm,则AB=_____,AC=_____.
三、解答题
13.如图,A,B表示两个仓库,要在A,B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
14.已知:如图,是线段的垂直平分线,E,F是上的两点.
求证:.
15.已知:如图,在中,,O是内一点,且.
求证:直线垂直平分线段.
16.如图,画AE⊥BC,CF⊥AD,垂足分别为E,F.
17.已知:如图,P是平分线上的一点,,垂足分别为C,D.
求证:
(1);
(2)是的垂直平分线.
18.为筹办一个大型运动会,某市政府打算修建一个大型体育中心.在选址过程中,有人建议该体育中心所在位置应与该市的三个城镇中心(图中以P,Q,R表示)的距离相等.
(1)根据上述建议,试在图(1)中画出体育中心G的位置;
(2)如果这三个城镇的位置如图(2)所示,是一个钝角,那么根据上述建议,体育中心G应在什么位置?
(3)你对上述建议有何评论?你对选址有什么建议?
试卷第4页,共5页
试卷第5页,共5页
参考答案
1.D
【解析】解:∵垂直平分线上任意一点,到线段两端点的距离相等,
∴到三角形三个顶点的距离相等的点是三角形三边中垂线的交点.
故选:D.
2.B
【解析】解:∵DE是△ABC中AC边上的垂直平分线,
∴AE=CE,
∵BC=8cm,AB=10cm,
∴△EBC的周长为:BC+BE+CE=BC+BE+AE=BC+AB=8+10=18(cm).
故选:B.
3.A
【解析】解:∵,
∴垂直平分线段,
∴,,,
故正确,不符合题意;
∴只有选项A不一定正确,符合题意.
故选:
4.B
【解析】根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
5.B
【解析】解:由DE是边AB的垂直平分线,
∴AD=BD,AE=BE,
由△ADC的周长为9cm,
∴AC+BC=9,
∵AE=3,
∴AB=6,
∴△ABC的周长是15cm,
故选:B.
6.B
【解析】解:∵顶点A、B为圆心,大于AB长为半径作圆弧
∴MN为AB的垂直平分线
∴AD=BD=5
∵BC=BD+CD
∴BC=AD+CD=5+3=8
故选B.
7.B
【解析】解:根据题意,
∵CD=CE,OE=OD,
∴AO是线段DE的垂直平分线,
∴∠AOB=90°;
则小意同学判断的依据是:线段中垂线上的点到线段两段距离相等;
故选:B.
8.5
【解析】∵垂直平分,,
∴,
∵点E是的中点,
∴.
故答案为:5.
9.线段的中点 垂直于这条线段 直线
【解析】解:经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
故填:线段的中点,垂直于这条线段,直线.
10.垂直
【解析】解:如图,连接、,
∵,
∴点A在线段的垂直平分线上,点D在线段的垂直平分线上,
∴根据两点确定一条直线得出直线是线段的垂直平分线,
故答案为:垂直.
11.线段AB的垂直平分线
【解析】因为PA=PB=3cm,
所以P点一定在线段AB的垂直平分线上.
故答案为:线段AB的垂直平分线.
12.AB=8cm AC=6cm
【解析】根据线段垂直平分线性质求出BD=DC,根据三角形周长AD+BD+AC=AB+AC=14cm,根据已知得出AC=AB-2cm,即可求出AC=6cm,AB=8cm.
故答案为8,6.
13.见解析.
【解析】解:连接AB,分别以A和B为圆心,以大于为半径的两弧交于点E和F,
作直线EF,与河岸交于点C,如图,则码头应建在点C处.
14.证明见解析
【解析】证明:是线段的垂直平分线,E,F是上的两点,
,
又,
(SSS),
.
15.证明见解析
【解析】证明:,,
,
是的垂直平分线.
即直线垂直平分线段.
16.见解析
【解析】解:如图,AE、CF为所作.
.
17.(1)证明见解析;(2)证明见解析.
【解析】解:(1)证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD;
(2)证明:∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP
∵由(1)知,OC=OD,
∴在△COE与△DOE中,
,
∴△COE≌△DOE,
∴CE=DE,OE⊥CD,即OP是CD的垂直平分线.
18.(1)见解析;(2)见解析;(3)见解析.
【解析】解:(1)如图,点G即为所求;
(2)如图,点G即为所求;
(3)上述建议非常合理,选址可以选在到该市的三个城镇中心的距离相等的位置.
答案第6页,共1页
答案第5页,共5页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
