2022年初中数学苏科版七年级下册7.1 探索直线平行的条件课时练习(Word版含答案)
文档属性
| 名称 | 2022年初中数学苏科版七年级下册7.1 探索直线平行的条件课时练习(Word版含答案) | 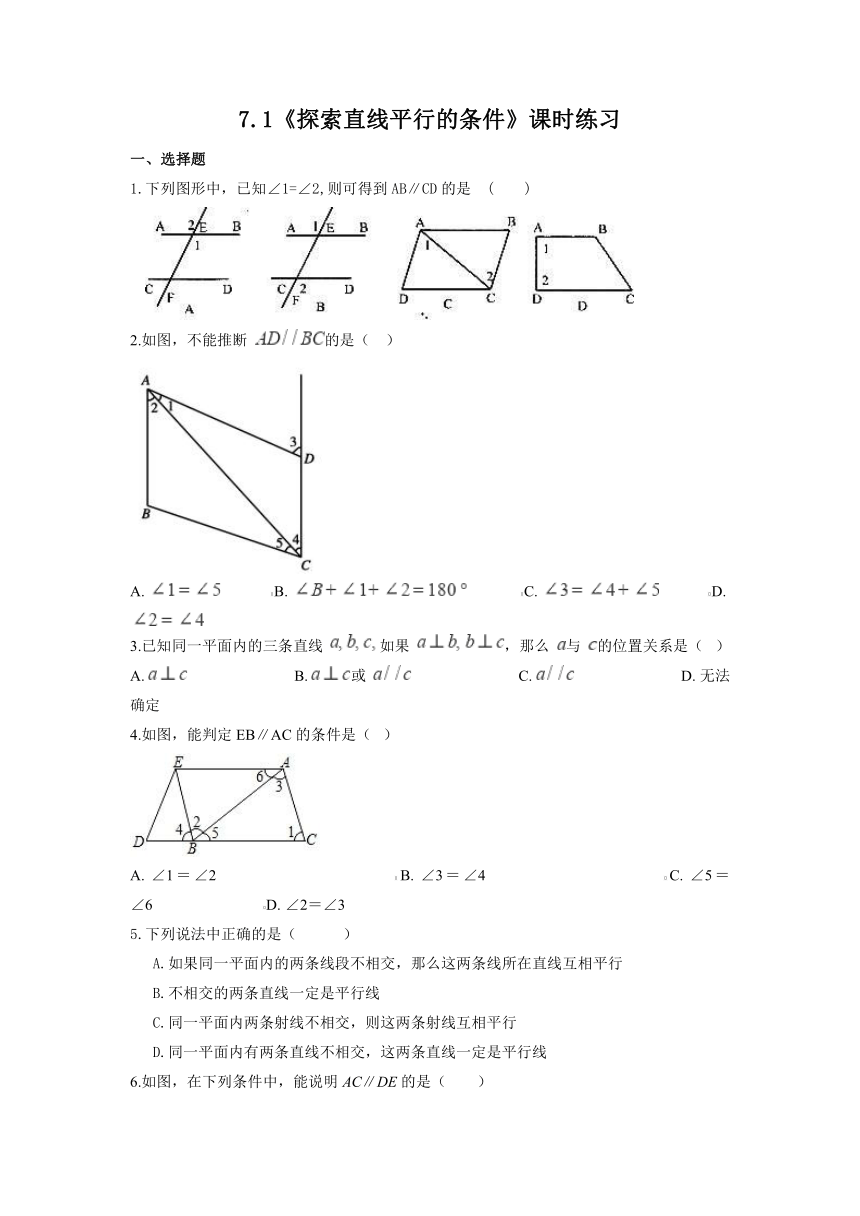 | |
| 格式 | docx | ||
| 文件大小 | 214.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 00:38:44 | ||
图片预览


文档简介
7.1《探索直线平行的条件》课时练习
一、选择题
1.下列图形中,已知∠1=∠2,则可得到AB∥CD的是 ( )
2.如图,不能推断 的是( )
A. B. C. D.
3.已知同一平面内的三条直线 如果 ,那么 与 的位置关系是( )
A. B. 或 C. D. 无法确定
4.如图,能判定EB∥AC的条件是( )
A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠6 D. ∠2=∠3
5.下列说法中正确的是( )
A.如果同一平面内的两条线段不相交,那么这两条线所在直线互相平行
B.不相交的两条直线一定是平行线
C.同一平面内两条射线不相交,则这两条射线互相平行
D.同一平面内有两条直线不相交,这两条直线一定是平行线
6.如图,在下列条件中,能说明AC∥DE的是( )
A. ∠A=∠CFD B. ∠BED=∠EDF C. ∠BED=∠A D. ∠A+∠AFD=180°
7.如图,下列条件: ①∠DCA=∠CAF , ②∠C =∠EDB , ③∠BAC+∠C=180°,④∠GDE +∠B=180°.其中能判断AB∥CD的是( )
A. ①④ B. ②③④ C. ①③④ D. ①②③
8.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A. 第一次向右拐40°,第二次向左拐140° B. 第一次向左拐40°,第二次向右拐40°
C. 第一次向左拐40°,第二次向右拐140° D. 第一次向右拐40°,第二次向右拐40°
二、填空题
9.如图,AC、BC分别平分∠DAB、∠ABE,且∠1与∠2互余, 则______∥_______,
理由是_________________________________________。
10.如图,若∠1=∠2,则 ∥ ,依据是 .
11.如图所示,与是________角,与是______角,与是__________角.
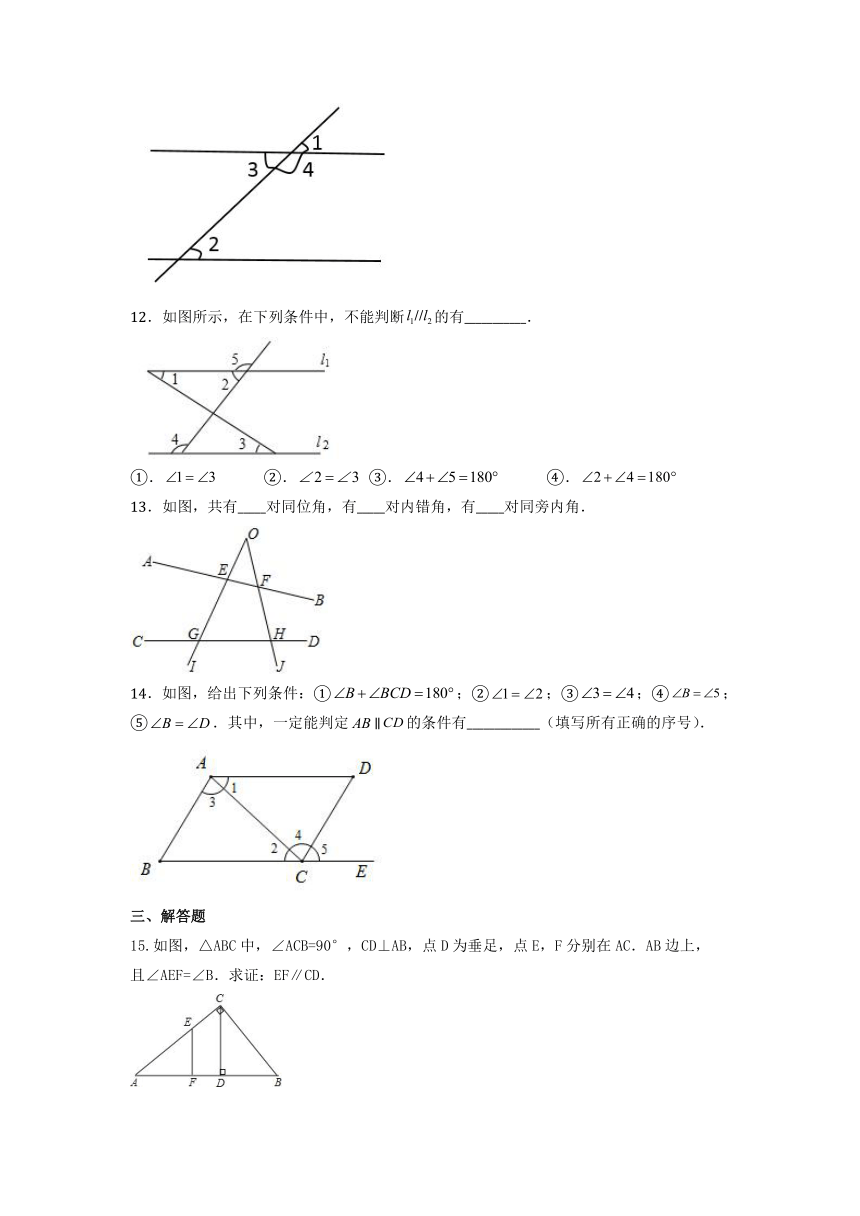
12.如图所示,在下列条件中,不能判断的有___________.
①. ②. ③. ④.
13.如图,共有_____对同位角,有_____对内错角,有_____对同旁内角.
14.如图,给出下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有_____________(填写所有正确的序号).
三、解答题
15.如图,△ABC中,∠ACB=90°,CD⊥AB,点D为垂足,点E,F分别在AC.AB边上,
且∠AEF=∠B.求证:EF∥CD.
16.如图,已知AB⊥AD,CD⊥AD,∠1=∠2,求证:DF∥AE.
17.如图, ,猜想 与 有怎样的位置关系,并说明理由.
18如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
参考答案
1.B
2.D
3.C
4.D
5.D
6.C
7.C
8.B
9.答案为:GD;HE;同旁内角互补,两直线平行
10.答案为:AD,BC
11.同位 同旁内 内错
12.②
13.20 12 12
14.①③④
15.证明:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠B=∠ACD,
∵∠AEF=∠B,
∴∠AEF=∠ACD,
∴EF∥CD.
16.【答案】 证明:∵AB⊥AD,CD⊥AD,
∴∠CDA=∠DAB=90°,
∵∠1=∠2,
∴∠CDA-∠2=∠DAB-∠1,
即:∠FDA=∠DAE,
∴ DF∥AE
【考点】平行线的判定
分析:由已知条件,可知∠CDA=∠DAB=90°,加之∠1=∠2,等量减等量,得到∠FDA=∠DAE,内错角相等即可判定.
17.【答案】 解:延长BE交CD于F.
∵∠BED=∠B+∠D,
∠BED=∠EFD+∠D,
∴∠B=∠EFD,
∴AB∥CD.
【考点】平行线的判定
分析:延长BE交CD于F,通过三角形外角的性质可证明∠B=∠EFD,则能证明AB∥CD.
18.【答案】 解:BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2= ∠ABC,∠3=∠4= ∠ADC(角平分线的定义).
∴∠1+∠3= (∠ABC+∠ADC)= ×180°=90°(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).
【考点】平行线的判定
分析:根据题意可知,∠1,∠2,∠3和∠4四个角的和为180°,根据角平分线定理即可求得∠3+∠1=90°,在直角三角形ABE中,根据∠1和∠AEB的和为90°,即可得到∠AEB=∠3,证明两条直线平行。
一、选择题
1.下列图形中,已知∠1=∠2,则可得到AB∥CD的是 ( )
2.如图,不能推断 的是( )
A. B. C. D.
3.已知同一平面内的三条直线 如果 ,那么 与 的位置关系是( )
A. B. 或 C. D. 无法确定
4.如图,能判定EB∥AC的条件是( )
A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠6 D. ∠2=∠3
5.下列说法中正确的是( )
A.如果同一平面内的两条线段不相交,那么这两条线所在直线互相平行
B.不相交的两条直线一定是平行线
C.同一平面内两条射线不相交,则这两条射线互相平行
D.同一平面内有两条直线不相交,这两条直线一定是平行线
6.如图,在下列条件中,能说明AC∥DE的是( )
A. ∠A=∠CFD B. ∠BED=∠EDF C. ∠BED=∠A D. ∠A+∠AFD=180°
7.如图,下列条件: ①∠DCA=∠CAF , ②∠C =∠EDB , ③∠BAC+∠C=180°,④∠GDE +∠B=180°.其中能判断AB∥CD的是( )
A. ①④ B. ②③④ C. ①③④ D. ①②③
8.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A. 第一次向右拐40°,第二次向左拐140° B. 第一次向左拐40°,第二次向右拐40°
C. 第一次向左拐40°,第二次向右拐140° D. 第一次向右拐40°,第二次向右拐40°
二、填空题
9.如图,AC、BC分别平分∠DAB、∠ABE,且∠1与∠2互余, 则______∥_______,
理由是_________________________________________。
10.如图,若∠1=∠2,则 ∥ ,依据是 .
11.如图所示,与是________角,与是______角,与是__________角.
12.如图所示,在下列条件中,不能判断的有___________.
①. ②. ③. ④.
13.如图,共有_____对同位角,有_____对内错角,有_____对同旁内角.
14.如图,给出下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有_____________(填写所有正确的序号).
三、解答题
15.如图,△ABC中,∠ACB=90°,CD⊥AB,点D为垂足,点E,F分别在AC.AB边上,
且∠AEF=∠B.求证:EF∥CD.
16.如图,已知AB⊥AD,CD⊥AD,∠1=∠2,求证:DF∥AE.
17.如图, ,猜想 与 有怎样的位置关系,并说明理由.
18如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
参考答案
1.B
2.D
3.C
4.D
5.D
6.C
7.C
8.B
9.答案为:GD;HE;同旁内角互补,两直线平行
10.答案为:AD,BC
11.同位 同旁内 内错
12.②
13.20 12 12
14.①③④
15.证明:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠B=∠ACD,
∵∠AEF=∠B,
∴∠AEF=∠ACD,
∴EF∥CD.
16.【答案】 证明:∵AB⊥AD,CD⊥AD,
∴∠CDA=∠DAB=90°,
∵∠1=∠2,
∴∠CDA-∠2=∠DAB-∠1,
即:∠FDA=∠DAE,
∴ DF∥AE
【考点】平行线的判定
分析:由已知条件,可知∠CDA=∠DAB=90°,加之∠1=∠2,等量减等量,得到∠FDA=∠DAE,内错角相等即可判定.
17.【答案】 解:延长BE交CD于F.
∵∠BED=∠B+∠D,
∠BED=∠EFD+∠D,
∴∠B=∠EFD,
∴AB∥CD.
【考点】平行线的判定
分析:延长BE交CD于F,通过三角形外角的性质可证明∠B=∠EFD,则能证明AB∥CD.
18.【答案】 解:BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2= ∠ABC,∠3=∠4= ∠ADC(角平分线的定义).
∴∠1+∠3= (∠ABC+∠ADC)= ×180°=90°(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).
【考点】平行线的判定
分析:根据题意可知,∠1,∠2,∠3和∠4四个角的和为180°,根据角平分线定理即可求得∠3+∠1=90°,在直角三角形ABE中,根据∠1和∠AEB的和为90°,即可得到∠AEB=∠3,证明两条直线平行。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
