2021-2022学年人教版九年级数学下册26.1.1 反比例函数 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.1.1 反比例函数 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 13:25:32 | ||
图片预览







文档简介
(共27张PPT)
人教版九年级上册数学
26.1.1反比例函数
学习目标
1、理解并掌握反比例函数的概念。
2、能判定一个给定的函数是否为反比例函数,并
会用待定系数法求函数解析式
3、经历反比例函数的形成过程,体验函数是描述
变量间对应关系的重要模型。
京沪铁路全程1463km,某列车的平均速度v km/h随运行时间t h的变化而变化;
情境问题一
V=
1463
t
_____
情境问题二
某小区要种植一个面积为1000 m的矩形草坪,它的长ym随宽xm的变化而变化;
2
y=
1000
x
____
情境问题三
北京市总面积为1.68x10 平方千米 ,人均占地面积s平方千米/人随全市人口n人的变化而变化;
S=
1.68x10
n
_______
4
4
比一比 说一说
上述四个解析式分别为:
V=
1463
t
____
y=
1000
x
___
S=
1.68x10
n
_____
4
1.你能说出这些表达式结构上的共同特征吗?
2.你能用一个一般形式表示出来吗?
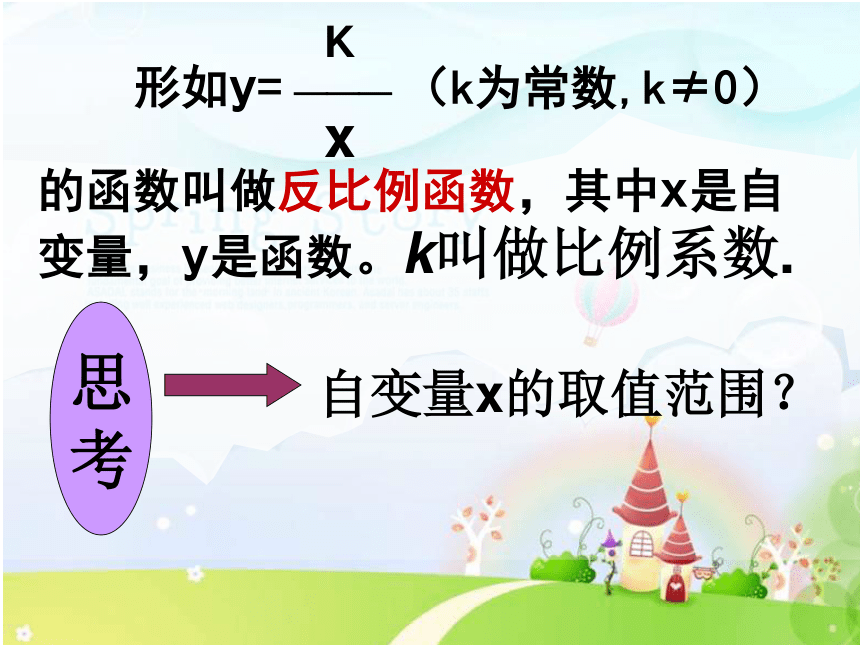
形如y= (k为常数,k≠0)
的函数叫做反比例函数,其中x是自变量,y是函数。k叫做比例系数.
K
x
___
思
考
自变量x的取值范围?
不具备 的形式,所以y不是x的反比例函数。
例1、下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
可以改写成 ,所以y是x的反比例函数,比例系数k=1。
不具备 的形式,所以y不是x的反比例函数。
y是x的反比例函数,比例系数k=4。
可以改写成 所以y是x的反比例函数,比例系数k=
y =
3
2x
y = 3x-1
y = 2x
y = 3x
y =
1
x2
y =
x
1
练习1、 你能帮下列函数找找家吗?
反比例函数
一次函数
反比例函数表达式几种不同形式呢?
思考:xy=4中y是x的反比例函数吗?
归 纳
y=
K
x
___
Xy=k
y=kx
-1
K为常数,
k≠0
1.若函数y=(m+2)x 是反比例函数,
则m_____,n_____;
2.若函数y=(m+3)x 是反比例函数,
则m=_____;
3.若函数y= 是反比例函数,则m=_______.
n-1
lml-4
m-1
x
____
lml
合作探究
=0
≠-2
3
-1
同学们,求函数解析式有一种特定的方法,你还记得吗?
待定系数法
4、已知y是x的反比例函数,当x=2时,y=6.
(1)求y与x之间的函数解析式;
(2)求当x=4时y的值。
解:(1)设此解析式为y= ,
把x=2,y=6代入得,
6=
k=12
此函数解析式为y= .
K
x
__
K
2
__
(2)把x=4
代入y= ,
得y= 3.
12
x
__
12
x
__
步骤要规范
欢乐城堡旅行开始啦!
难度指数:☆
第一关 临行前的准备
1、写出下列函数关系式,并指出它们各是什么函数
(1)平行四边形面积是24cm2,它的一边长xcm和这边上的高hcm之间的关系是 .
难度指数:☆
难度指数:☆☆
第二关 逐见真面目
2、若y是x-1的反比例函数,则x的取值范围是 .
难度指数:☆☆
难度指数:☆☆☆
第三关 勇往直前
3、若函数y=(3+m)x 是反比例函数,则m的取值是 .
8-m
2
难度指数:☆☆☆
难度指数:☆☆☆☆
第四关 探究无止境
4.已知y与x 成反比例关系,且当x=3时y=4,
(1)求y与x之间的函数解析式;
(2)当x=-2时y的值。
2
难度指数:☆☆☆☆
难度指数:☆☆☆☆☆
第五关 冲刺登顶
5、已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,
y=5.
(1)求y与x的函数关系式.
(2)当x=-2时,求函数y的值.
难度指数:☆☆☆☆☆
恭喜!你通关啦!
1.反比例函数的定义及其形式;
2.并利用其进行判别和计算;
3.学会待定系数法求其解析式及相关运用;
今天你的收获是什么呢?
Thank you!
人教版九年级上册数学
26.1.1反比例函数
学习目标
1、理解并掌握反比例函数的概念。
2、能判定一个给定的函数是否为反比例函数,并
会用待定系数法求函数解析式
3、经历反比例函数的形成过程,体验函数是描述
变量间对应关系的重要模型。
京沪铁路全程1463km,某列车的平均速度v km/h随运行时间t h的变化而变化;
情境问题一
V=
1463
t
_____
情境问题二
某小区要种植一个面积为1000 m的矩形草坪,它的长ym随宽xm的变化而变化;
2
y=
1000
x
____
情境问题三
北京市总面积为1.68x10 平方千米 ,人均占地面积s平方千米/人随全市人口n人的变化而变化;
S=
1.68x10
n
_______
4
4
比一比 说一说
上述四个解析式分别为:
V=
1463
t
____
y=
1000
x
___
S=
1.68x10
n
_____
4
1.你能说出这些表达式结构上的共同特征吗?
2.你能用一个一般形式表示出来吗?
形如y= (k为常数,k≠0)
的函数叫做反比例函数,其中x是自变量,y是函数。k叫做比例系数.
K
x
___
思
考
自变量x的取值范围?
不具备 的形式,所以y不是x的反比例函数。
例1、下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
可以改写成 ,所以y是x的反比例函数,比例系数k=1。
不具备 的形式,所以y不是x的反比例函数。
y是x的反比例函数,比例系数k=4。
可以改写成 所以y是x的反比例函数,比例系数k=
y =
3
2x
y = 3x-1
y = 2x
y = 3x
y =
1
x2
y =
x
1
练习1、 你能帮下列函数找找家吗?
反比例函数
一次函数
反比例函数表达式几种不同形式呢?
思考:xy=4中y是x的反比例函数吗?
归 纳
y=
K
x
___
Xy=k
y=kx
-1
K为常数,
k≠0
1.若函数y=(m+2)x 是反比例函数,
则m_____,n_____;
2.若函数y=(m+3)x 是反比例函数,
则m=_____;
3.若函数y= 是反比例函数,则m=_______.
n-1
lml-4
m-1
x
____
lml
合作探究
=0
≠-2
3
-1
同学们,求函数解析式有一种特定的方法,你还记得吗?
待定系数法
4、已知y是x的反比例函数,当x=2时,y=6.
(1)求y与x之间的函数解析式;
(2)求当x=4时y的值。
解:(1)设此解析式为y= ,
把x=2,y=6代入得,
6=
k=12
此函数解析式为y= .
K
x
__
K
2
__
(2)把x=4
代入y= ,
得y= 3.
12
x
__
12
x
__
步骤要规范
欢乐城堡旅行开始啦!
难度指数:☆
第一关 临行前的准备
1、写出下列函数关系式,并指出它们各是什么函数
(1)平行四边形面积是24cm2,它的一边长xcm和这边上的高hcm之间的关系是 .
难度指数:☆
难度指数:☆☆
第二关 逐见真面目
2、若y是x-1的反比例函数,则x的取值范围是 .
难度指数:☆☆
难度指数:☆☆☆
第三关 勇往直前
3、若函数y=(3+m)x 是反比例函数,则m的取值是 .
8-m
2
难度指数:☆☆☆
难度指数:☆☆☆☆
第四关 探究无止境
4.已知y与x 成反比例关系,且当x=3时y=4,
(1)求y与x之间的函数解析式;
(2)当x=-2时y的值。
2
难度指数:☆☆☆☆
难度指数:☆☆☆☆☆
第五关 冲刺登顶
5、已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,
y=5.
(1)求y与x的函数关系式.
(2)当x=-2时,求函数y的值.
难度指数:☆☆☆☆☆
恭喜!你通关啦!
1.反比例函数的定义及其形式;
2.并利用其进行判别和计算;
3.学会待定系数法求其解析式及相关运用;
今天你的收获是什么呢?
Thank you!
