2021-2022学年鲁教版八年级数学下册6.3正方形的性质与判定 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册6.3正方形的性质与判定 同步练习题(Word版含答案) | 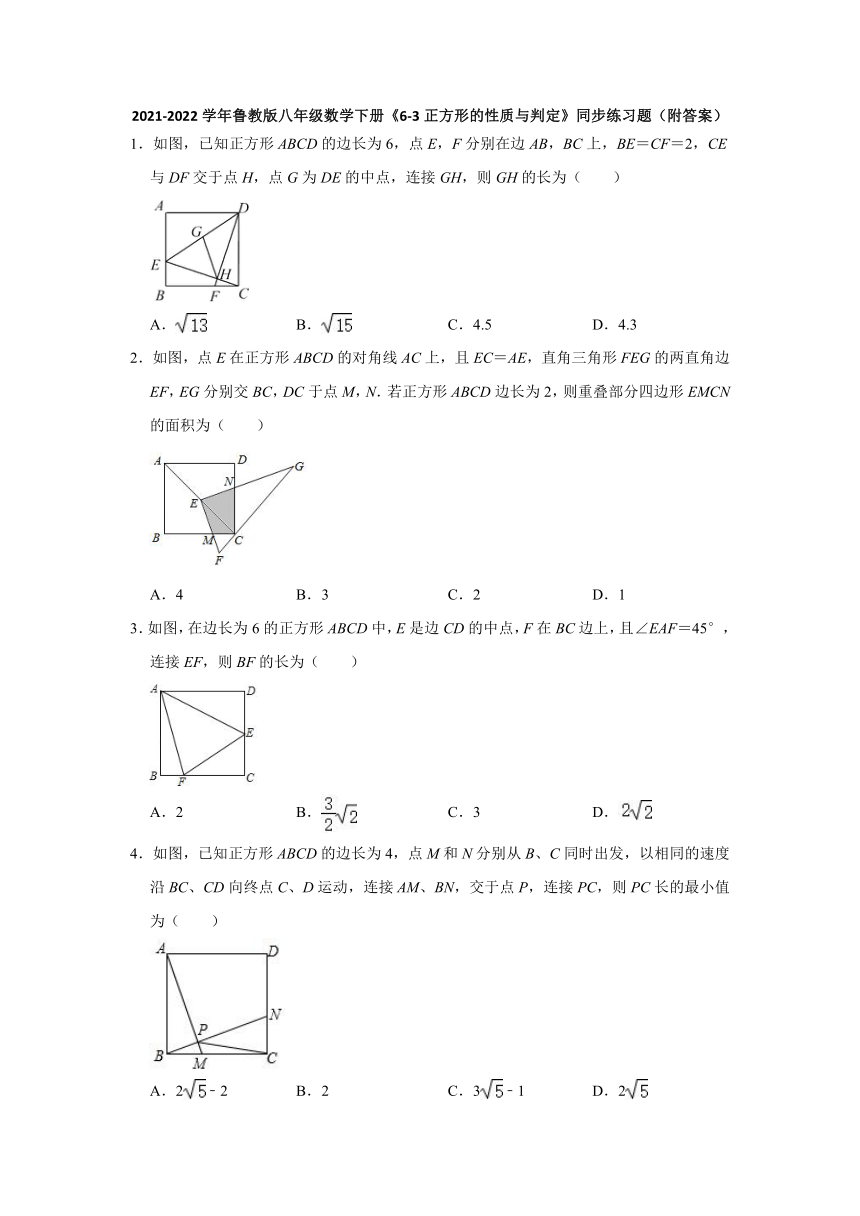 | |
| 格式 | docx | ||
| 文件大小 | 429.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 11:42:25 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步练习题(附答案)
1.如图,已知正方形ABCD的边长为6,点E,F分别在边AB,BC上,BE=CF=2,CE与DF交于点H,点G为DE的中点,连接GH,则GH的长为( )
A. B. C.4.5 D.4.3
2.如图,点E在正方形ABCD的对角线AC上,且EC=AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD边长为2,则重叠部分四边形EMCN的面积为( )
A.4 B.3 C.2 D.1
3.如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
A.2 B. C.3 D.
4.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为( )
A.2﹣2 B.2 C.3﹣1 D.2
5.如图,在正方形ABCD中,点E是CD的中点,点F是AD的中点,BE与CF相交于点P,设AB=a.得到以下结论:
①BE⊥CF;②AP=a;③CP=a
则上述结论正确的是( )
A.①② B.①③ C.②③ D.①②③
6.如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
A. B.5 C.5 D.
7.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形 B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
8.如图,以△ABC的各边为边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG,对于四边形ADEG的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.若∠BAC≠45°,则四边形ADEG是平行四边形
B.若∠BAC=90°,则四边形ADEG是矩形
C.若AC=AB,则四边形ADEG是菱形
D.若∠BAC=135°且AC=AB,则四边形ADEG是正方形
9.如图,已知四边形ABCD为正方形AB=2,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC延长线于点F,以DE、EF为邻边作矩形DEFG,连接CG.在下列结论中:①矩形DEFG是正方形; ②2CE+CG=AD;③CG平分∠DCF;④CE=CF.其中正确的结论有( )
A.①③ B.②④ C.①②③ D.①②③④
10.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④,其中正确结论有( )个.
A.1 B.2 C.3 D.4
11.如图,已知:PA=2,PB=4,以AB为边作正方形ABCD,使P、D两点落在直线AB的两侧.当∠APB=45°时,则PD的长为 .
12.如图,边长为2的正方形ABCD中,点E,F在边BC上,且BE=CF=﹣1,在边AB或CD上有一点P,若∠EPF=30°,则PE的长为 .
13.正方形ABCD中,AB=2,点P为射线BC上一动点,BE⊥AP,垂足为E,连接DE、DP,当点P为BC中点时,S△ADE= ;在点P运动的过程中,的最小值为 .
14.已知:正方形ABCD中,E为BC的中点,BP=2AP,F为AD上一点,EF交CP于O,∠POF=45°,若△APF的面积为,则线段EF的长为 .
15.如图,P为正方形ABCD的边BC的中点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,若正方形的边长为2,则CE= .
16.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
17.如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF.
(1)当DG=2时,求证:四边形EFGH是正方形;
(2)当△FCG的面积为2时,求CG的值.
18.如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.
19.如图所示,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=6,∠ABE=45°,若AE=5,求CE的长.
20.已知:如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
求证:(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
参考答案
1.解:∵四边形ABCD为正方形,
∴∠B=∠DCF=90°,BC=DC,
在△CBE和△DCF中,
,
∴△CBE≌△DCF(SAS),
∴∠BCE=∠CDF,
∵∠BCE+∠DCH=90°,
∴∠CDF+∠DCH=90°,
∴∠DHC=∠DHE=90°,
∵点G为DE的中点,
∴GH=DE,
∵AD=AB=6,AE=AB﹣BE=6﹣2=4,
∴DE===2,
∴GH=.
故选:A.
2.解:过E作EP⊥BC于点P,EQ⊥CD于点Q,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,
在△EPM和△EQN中,
,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为2,
∴AC=2,
∵EC=AE,
∴EC=,
∴EP=PC=1,
∴正方形PCQE的面积=EP2=1.
故选:D.
3.证明:∵四边形ABCD是正方形,
∴AB=AD,
∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图:
∴∠BAF=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAF+∠DAE=45°,
∴∠EAF=∠EAG,
∵∠ADG=∠ADC=∠B=90°,
∴∠EDG=180°,点E、D、G共线,
在△AFE和△AGE中,
,
∴△AFE≌△AGE(SAS),
∴EF=EG,
即:EF=EG=ED+DG,
∵E为CD的中点,边长为6的正方形ABCD,
∴CD=BC=6,DE=CE=3,∠C=90°,
∴设BF=x,则CF=6﹣x,EF=3+x,
在Rt△CFE中,由勾股定理得:
EF2=CE2+CF2,
∴(3+x)2=32+(6﹣x)2,
解得:x=2,
即BF=2,
故选:A.
4.解:由题意得:BM=CN,
∵四边形ABCD是正方形,
∴∠ABM=∠BCN=90°,AB=BC=4,
在△ABM和△BCN中,AB=BC,∠ABM=∠BCN,MB=CN,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠ABP+∠CBN=90°,
∴∠ABP+∠BAM=90°,
∴∠APB=90°,
∴点p是以AP为半径的圆上远动,设圆心为O,运动路径一条弧,是这个圆的,如图所示:
连接OC交圆O于P,此时PC最小,
∵AB=4,
∴OP=OB=2,
由勾股定理得:OC==2,
∴PC=OC﹣OP=2﹣2;
故选:A.
5.解:在△CDF和△BCE中
∴△CDF≌△BCE(SAS)
∴∠CEB=∠CFD
∵∠DCF+∠CFD=90°
∴∠DCF+∠CEB=90°
∴∠EPC=90°
∴①正确;
如图延长CF交BA延长线于点M,
在△CFD和△MFA中
∴△CFD≌△MFA(ASA)
∴CD=MA=AB=a,
∵BP⊥CF
∴AP为Rt△MPB斜边BM上的中线,是斜边的一半,即AP=BM=×2a=a,
∴②正确;
∵CP⊥BE
∴CP×BE=CE×BC=
∵BE===
∴CP===
∴③正确
故选:D.
6.解:如图所示,连接CN、DM、AC,
∵点C关于直线DE的对称点为M,
∴CN=MN,CD=DM,
∴∠NCM=∠NMC,∠DCM=∠DMC,
∴∠DCN=∠DMN,
在正方形ABCD中,AD=CD,
∴AD=DM,
∴∠DAM=∠DMN,
∴∠DCN=∠DAM,
∵∠ACN+∠CAN=∠DCA﹣∠DCN+∠CAD+∠DAM=∠DCA+∠CAD=90°,
∴∠ANC=180°﹣90°=90°,
∴△ACN是直角三角形,
∴AC===5,
∴正方形ABCD的边长=AC=.
故选:D.
7.解:①由矩形的判定“对角线相等的平行四边形是矩形”可知,A正确;
②由菱形的判定“有一组邻边相等的平行四边形是菱形”可知,B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④在平行四边形ABCD中,
∵∠DAB=90°,
∴平行四边形ABCD是矩形,而不能判定其是正方形,故D错误;
故选:D.
8.解:A、∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,
∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.
∴∠ABC=∠EBD(同为∠EBA的余角).
在△BDE和△BAC中,
,
∴△BDE≌△BAC(SAS),
∴DE=AC=AG,∠BAC=∠BDE.
∵AD是正方形ABDI的对角线,
∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,
∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD
=360°﹣90°﹣∠BAC﹣45°
=225°﹣∠BAC,
∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,
∴DE∥AG,
∴四边形ADEG是平行四边形(一组对边平行且相等),正确,故本选项不符合题意;
B、∵四边形ABDI和四边形ACHG是正方形,
∴∠DAI=45°,∠GAC=90°,
∵∠BAC=90°,
∴∠DAG=360°﹣45°﹣90°﹣90°=135°,
∵四边形ADEG是平行四边形,
∴四边形ADEG不是矩形,错误,故本选项符合题意;
C、∵四边形ADEG是平行四边形,
∴若要四边形ADEG是菱形,则需AD=AG,即AD=AC.
∵AD=AB,
∴当AB=AD,即AB=AC时,四边形ADEG是菱形,正确,故本选项不符合题意;
D、∵当∠BAC=135°时,∠DAG=360°﹣45°﹣90°﹣135°=90°,即平行四边形ADEG是平行四边形,
∵当AB=AD,即AB=AC时,四边形ADEG是菱形,
∴四边形ADEG是正方形,
即当∠BAC=135°且AC=AB时,四边形ADEG是正方形,正确,故本选项不符合题意;
故选:B.
9.解:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,
∴NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形;故①正确;
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=CE+CG=AD,故③错误;
当DE⊥AC时,点C与点F重合,
∴CE不一定等于CF,故④错误,
故选:A.
10.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°,
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,∠BAE=∠DAF,
故①正确;
∵∠BAE+∠DAF=30°,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,
故②正确;
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵Rt△ABE≌Rt△ADF,
∴AE=AF,
∴AC垂直平分EF,
∴EG=FG,
故③正确;
∵∠ECF=90°,EG=FG,
∴CG=EF,
设EC=FC=x,由勾股定理,得EF==x,
∴CG=EF=x=CE,
故④正确;
综上所述,正确的有①②③④,共4个.
故选:D.
11.解:∵AD=AB,∠DAB=90°,
∴把△APD绕点A顺时针旋转90°得到△AFB,AD与AB重合,PA旋转到AF的位置,如图,
∴AP=AF,∠PAF=90°,PD=FB,
∴△APF为等腰直角三角形,
∴∠APF=45°,PF=AP=2,
∴∠BPF=∠APB+∠APF=45°+45°=90°,
在Rt△FBP中,PB=4,PF=2,
∴由勾股定理得FB===2,
∴PD=2,
故答案为:2.
12.解:如图,连接AC,BD交于点O,连接OE,OF,过点O作OH⊥BC于点H,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,∠ABC=∠BCD=90°,∠OBC=∠OCB=45°,OA=OB=OC=OD,
∵OH⊥BC,
∴OH=BH=CH=,
∴EH=BH﹣BE=1,
∴OE=2.
同理可得:OF=2,
又∵EF=BC﹣BE﹣CF=2,
∴△OEF是等边三角形,
∴∠EOF=60°,
以点O为圆心,OE长为半径作⊙O,分别交AB于点P1,P2,交CD于点P3,P4,
则∠EP1F=∠EP2F=∠EP3F=∠EP4F=∠EOF=30°,
∵OE=OF,OH⊥BC,
∴EH=FH=1,
∴BE=CF=BH﹣EH=﹣1,
同理:AP2=BP1=BE=CF=CP4=DP3=﹣1,
①当∠EP1F=30°时,
在Rt△P1BE中,∵BP1=BE=﹣1,
∴P1E=BE=﹣;
②当∠EP2F=30°时,
在Rt△P2BE中,BP2=AB﹣AP2=+1,
则P2E==2;
③当∠EP3F=30°时,
在Rt△P3CE中,CP3=CE=+1,
∴P3E=CE=+;
④当∠EP4F=30°时,
在Rt△P4CE中,CP4=﹣1,CE=+1,
则P4E==2.
综上,PE=﹣或2或+.
故答案为:﹣或2或+.
13.解:如图,过点E作EF⊥AD于F,
∵∠BAD=∠EFD=90°,
∴EF∥AB,
∴∠BAP=∠AEF=∠BAE,
∵点P为BC中点,
∴BP=AB=1,
∴AP==,
∴==,
∴AE=,
∴EF=,
∴S△ADE=AD EF=×2×=;
如图,把△APB绕点A逆时针旋转90°得到△ADG,取AG的中点H,连接HD、HP,
由旋转的性质,得:AG=AP,∠1=∠2,∠ADG=∠ABP=90°,
∴∠2+∠3=∠1+∠3=90°,AH=HD=AP,
∵AH2+AP2=HP2,
∴HP=AP,
∵HD+DP≥HP,
∴AP+DP≥AP,
∴DP≥AP,
∴的最小值为.
故答案为:; .
14.解:如图:过E作EM⊥OC,垂足为M,
过点O作ON⊥BC,垂足为N,
过点F作FP⊥BC,垂足为G,设EM=x,
∴∠CME=∠CBP=90°,
∴CM=x,
又∵∠EOC=∠POF=45°,
∴OM=x,OE=x,
∴OC=OM+CM=x,CE==x,
∴正方形的边长为2CE=x,
∴AP=x,
在△COE中,S△COE=OC BM=ON EC,
解得:ON=x,
∴NE==x,
∵ON⊥BC,GF⊥BC,
∴ON∥FG,
∴EG=x,
∴BG=BE﹣EG=()x=x,
∵AB∥FPGAF∥BG,
∴四边形ABGF为矩形,
∴AF=BG=x,
∴S△APF=AP AF= x x=,
解得:x=,
∴EF=××=.
故答案为:.
15.解:如图,过C作CH⊥AE于H,
∵AG=GE,
∴AB=BE,
∴∠BAE=BEA,
∵BG⊥AE,
∴∠BGP=∠CHP=90°,
∵P为BC的中点,
∴BP=CP,
在△BGP和△CHP中,
,
∴△BGP≌△CHP(AAS),
∴BG=CH,∠GBP=∠PCH,
∵四边形ABCD是正方形,
∴AB=BC,
∴BC=BE,
∴∠BCE=∠BEC,
∵∠ABC=∠ABG+∠GBP=90°,∠ABG+∠BAG=90°,
∴∠GBP=∠BAG,
∴∠PCH=∠BEP,
∴∠HCE=∠HEC,
∴CH=EH,
∵∠CHE=90°,
∴CE=CH,即CE=BG,
在Rt△ABP中,AB=2,BP=BC=1,
∴AP==,
∵S△ABP=AB BP=AP BG,
∴BG==,
∴CE=×=,
故答案为.
16.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
17.(1)证明:在矩形ABCD中,有∠A=∠D=90°,
∴∠DGH+∠DHG=90°.
在菱形EFGH中,EH=GH
∵AH=2,DG=2,
∴AH=DG,
∴Rt△AEH≌Rt△DHG(HL).
∴∠AHE=∠DGH.
∴∠AHE+∠DHG=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
(2)过F作FM⊥DC于M,则∠FMG=90°.
∴∠A=∠FMG=90°.连接EG.
由矩形和菱形性质,知AB∥DC,HE∥GF,
∴∠AEG=∠MGE,∠HEG=∠FGE,
∴∠AEH=∠MGF.
∵EH=GF,
∴△AEH≌△MGF.
∴FM=AH=2.
∵S △FCG=,
∴CG=2.
18.解:作DE⊥BC,交BC延长线于E,如图,
∵DP⊥AB,ABC=90°,
∴四边形BEDP为矩形,
∴∠PDE=90°,即∠CDE+∠PDC=90°,
∵∠ADC=90°,即∠ADP+∠PDC=90°,
∴∠ADP=∠CDE,
在△ADP和△CDE中,
,
∴△ADP≌△CDE,
∴DP=DE,S△ADP=S△CDE,
∴四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,
∴DP2=36,
∴DP=6.
19.解:如图,过点B作BF⊥AD交DA的延长线于F,
∵AD∥BC,∠D=90°,BC=CD,
∴四边形BCDF是正方形,
把△BCE绕点B顺时针旋转90°得到△BFG,
则CE=FG,BE=BG,∠CBE=∠FBG,
∵∠ABE=45°,
∴∠ABG=∠ABF+∠FBG=∠ABF+∠CBE=90°﹣∠ABE=90°﹣45°=45°,
∴∠ABE=∠ABG,
在△ABE和△ABG中,
,
∴△ABE≌△ABG(SAS),
∴AE=AG,
∴AF+CE=AF+FG=AG=AE,
设CE=x,则DE=6﹣x,AF=5﹣x,
∴AD=6﹣(5﹣x)=x+1,
在Rt△ADE中,AD2+DE2=AE2,
即(x+1)2+(6﹣x)2=52,
整理得,x2﹣5x+6=0,
解得x1=2,x2=3,
所以CE的长度是2或3.
20.证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AF=BP=CQ=DE,
∴DF=CE=BQ=AP,
在△APF和△DFE和△CEQ和△BQP中,
,
∴△APF≌△DFE≌△CEQ≌△BQP(SAS),
∴EF=FP=PQ=QE;
(2)∵EF=FP=PQ=QE,
∴四边形EFPQ是菱形,
∵△APF≌△BQP,
∴∠AFP=∠BPQ,
∵∠AFP+∠APF=90°,
∴∠APF+∠BPQ=90°,
∴∠FPQ=90°,
∴四边形EFPQ是正方形.
1.如图,已知正方形ABCD的边长为6,点E,F分别在边AB,BC上,BE=CF=2,CE与DF交于点H,点G为DE的中点,连接GH,则GH的长为( )
A. B. C.4.5 D.4.3
2.如图,点E在正方形ABCD的对角线AC上,且EC=AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD边长为2,则重叠部分四边形EMCN的面积为( )
A.4 B.3 C.2 D.1
3.如图,在边长为6的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
A.2 B. C.3 D.
4.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为( )
A.2﹣2 B.2 C.3﹣1 D.2
5.如图,在正方形ABCD中,点E是CD的中点,点F是AD的中点,BE与CF相交于点P,设AB=a.得到以下结论:
①BE⊥CF;②AP=a;③CP=a
则上述结论正确的是( )
A.①② B.①③ C.②③ D.①②③
6.如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
A. B.5 C.5 D.
7.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形 B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
8.如图,以△ABC的各边为边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG,对于四边形ADEG的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.若∠BAC≠45°,则四边形ADEG是平行四边形
B.若∠BAC=90°,则四边形ADEG是矩形
C.若AC=AB,则四边形ADEG是菱形
D.若∠BAC=135°且AC=AB,则四边形ADEG是正方形
9.如图,已知四边形ABCD为正方形AB=2,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC延长线于点F,以DE、EF为邻边作矩形DEFG,连接CG.在下列结论中:①矩形DEFG是正方形; ②2CE+CG=AD;③CG平分∠DCF;④CE=CF.其中正确的结论有( )
A.①③ B.②④ C.①②③ D.①②③④
10.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④,其中正确结论有( )个.
A.1 B.2 C.3 D.4
11.如图,已知:PA=2,PB=4,以AB为边作正方形ABCD,使P、D两点落在直线AB的两侧.当∠APB=45°时,则PD的长为 .
12.如图,边长为2的正方形ABCD中,点E,F在边BC上,且BE=CF=﹣1,在边AB或CD上有一点P,若∠EPF=30°,则PE的长为 .
13.正方形ABCD中,AB=2,点P为射线BC上一动点,BE⊥AP,垂足为E,连接DE、DP,当点P为BC中点时,S△ADE= ;在点P运动的过程中,的最小值为 .
14.已知:正方形ABCD中,E为BC的中点,BP=2AP,F为AD上一点,EF交CP于O,∠POF=45°,若△APF的面积为,则线段EF的长为 .
15.如图,P为正方形ABCD的边BC的中点,BG⊥AP于点G,在AP的延长线上取点E,使AG=GE,若正方形的边长为2,则CE= .
16.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
17.如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF.
(1)当DG=2时,求证:四边形EFGH是正方形;
(2)当△FCG的面积为2时,求CG的值.
18.如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.
19.如图所示,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=6,∠ABE=45°,若AE=5,求CE的长.
20.已知:如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE.
求证:(1)EF=FP=PQ=QE;
(2)四边形EFPQ是正方形.
参考答案
1.解:∵四边形ABCD为正方形,
∴∠B=∠DCF=90°,BC=DC,
在△CBE和△DCF中,
,
∴△CBE≌△DCF(SAS),
∴∠BCE=∠CDF,
∵∠BCE+∠DCH=90°,
∴∠CDF+∠DCH=90°,
∴∠DHC=∠DHE=90°,
∵点G为DE的中点,
∴GH=DE,
∵AD=AB=6,AE=AB﹣BE=6﹣2=4,
∴DE===2,
∴GH=.
故选:A.
2.解:过E作EP⊥BC于点P,EQ⊥CD于点Q,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,
在△EPM和△EQN中,
,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为2,
∴AC=2,
∵EC=AE,
∴EC=,
∴EP=PC=1,
∴正方形PCQE的面积=EP2=1.
故选:D.
3.证明:∵四边形ABCD是正方形,
∴AB=AD,
∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图:
∴∠BAF=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAF+∠DAE=45°,
∴∠EAF=∠EAG,
∵∠ADG=∠ADC=∠B=90°,
∴∠EDG=180°,点E、D、G共线,
在△AFE和△AGE中,
,
∴△AFE≌△AGE(SAS),
∴EF=EG,
即:EF=EG=ED+DG,
∵E为CD的中点,边长为6的正方形ABCD,
∴CD=BC=6,DE=CE=3,∠C=90°,
∴设BF=x,则CF=6﹣x,EF=3+x,
在Rt△CFE中,由勾股定理得:
EF2=CE2+CF2,
∴(3+x)2=32+(6﹣x)2,
解得:x=2,
即BF=2,
故选:A.
4.解:由题意得:BM=CN,
∵四边形ABCD是正方形,
∴∠ABM=∠BCN=90°,AB=BC=4,
在△ABM和△BCN中,AB=BC,∠ABM=∠BCN,MB=CN,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠ABP+∠CBN=90°,
∴∠ABP+∠BAM=90°,
∴∠APB=90°,
∴点p是以AP为半径的圆上远动,设圆心为O,运动路径一条弧,是这个圆的,如图所示:
连接OC交圆O于P,此时PC最小,
∵AB=4,
∴OP=OB=2,
由勾股定理得:OC==2,
∴PC=OC﹣OP=2﹣2;
故选:A.
5.解:在△CDF和△BCE中
∴△CDF≌△BCE(SAS)
∴∠CEB=∠CFD
∵∠DCF+∠CFD=90°
∴∠DCF+∠CEB=90°
∴∠EPC=90°
∴①正确;
如图延长CF交BA延长线于点M,
在△CFD和△MFA中
∴△CFD≌△MFA(ASA)
∴CD=MA=AB=a,
∵BP⊥CF
∴AP为Rt△MPB斜边BM上的中线,是斜边的一半,即AP=BM=×2a=a,
∴②正确;
∵CP⊥BE
∴CP×BE=CE×BC=
∵BE===
∴CP===
∴③正确
故选:D.
6.解:如图所示,连接CN、DM、AC,
∵点C关于直线DE的对称点为M,
∴CN=MN,CD=DM,
∴∠NCM=∠NMC,∠DCM=∠DMC,
∴∠DCN=∠DMN,
在正方形ABCD中,AD=CD,
∴AD=DM,
∴∠DAM=∠DMN,
∴∠DCN=∠DAM,
∵∠ACN+∠CAN=∠DCA﹣∠DCN+∠CAD+∠DAM=∠DCA+∠CAD=90°,
∴∠ANC=180°﹣90°=90°,
∴△ACN是直角三角形,
∴AC===5,
∴正方形ABCD的边长=AC=.
故选:D.
7.解:①由矩形的判定“对角线相等的平行四边形是矩形”可知,A正确;
②由菱形的判定“有一组邻边相等的平行四边形是菱形”可知,B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④在平行四边形ABCD中,
∵∠DAB=90°,
∴平行四边形ABCD是矩形,而不能判定其是正方形,故D错误;
故选:D.
8.解:A、∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,
∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.
∴∠ABC=∠EBD(同为∠EBA的余角).
在△BDE和△BAC中,
,
∴△BDE≌△BAC(SAS),
∴DE=AC=AG,∠BAC=∠BDE.
∵AD是正方形ABDI的对角线,
∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,
∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD
=360°﹣90°﹣∠BAC﹣45°
=225°﹣∠BAC,
∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,
∴DE∥AG,
∴四边形ADEG是平行四边形(一组对边平行且相等),正确,故本选项不符合题意;
B、∵四边形ABDI和四边形ACHG是正方形,
∴∠DAI=45°,∠GAC=90°,
∵∠BAC=90°,
∴∠DAG=360°﹣45°﹣90°﹣90°=135°,
∵四边形ADEG是平行四边形,
∴四边形ADEG不是矩形,错误,故本选项符合题意;
C、∵四边形ADEG是平行四边形,
∴若要四边形ADEG是菱形,则需AD=AG,即AD=AC.
∵AD=AB,
∴当AB=AD,即AB=AC时,四边形ADEG是菱形,正确,故本选项不符合题意;
D、∵当∠BAC=135°时,∠DAG=360°﹣45°﹣90°﹣135°=90°,即平行四边形ADEG是平行四边形,
∵当AB=AD,即AB=AC时,四边形ADEG是菱形,
∴四边形ADEG是正方形,
即当∠BAC=135°且AC=AB时,四边形ADEG是正方形,正确,故本选项不符合题意;
故选:B.
9.解:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,
∴NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形;故①正确;
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=CE+CG=AD,故③错误;
当DE⊥AC时,点C与点F重合,
∴CE不一定等于CF,故④错误,
故选:A.
10.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°,
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,∠BAE=∠DAF,
故①正确;
∵∠BAE+∠DAF=30°,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,
故②正确;
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵Rt△ABE≌Rt△ADF,
∴AE=AF,
∴AC垂直平分EF,
∴EG=FG,
故③正确;
∵∠ECF=90°,EG=FG,
∴CG=EF,
设EC=FC=x,由勾股定理,得EF==x,
∴CG=EF=x=CE,
故④正确;
综上所述,正确的有①②③④,共4个.
故选:D.
11.解:∵AD=AB,∠DAB=90°,
∴把△APD绕点A顺时针旋转90°得到△AFB,AD与AB重合,PA旋转到AF的位置,如图,
∴AP=AF,∠PAF=90°,PD=FB,
∴△APF为等腰直角三角形,
∴∠APF=45°,PF=AP=2,
∴∠BPF=∠APB+∠APF=45°+45°=90°,
在Rt△FBP中,PB=4,PF=2,
∴由勾股定理得FB===2,
∴PD=2,
故答案为:2.
12.解:如图,连接AC,BD交于点O,连接OE,OF,过点O作OH⊥BC于点H,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,∠ABC=∠BCD=90°,∠OBC=∠OCB=45°,OA=OB=OC=OD,
∵OH⊥BC,
∴OH=BH=CH=,
∴EH=BH﹣BE=1,
∴OE=2.
同理可得:OF=2,
又∵EF=BC﹣BE﹣CF=2,
∴△OEF是等边三角形,
∴∠EOF=60°,
以点O为圆心,OE长为半径作⊙O,分别交AB于点P1,P2,交CD于点P3,P4,
则∠EP1F=∠EP2F=∠EP3F=∠EP4F=∠EOF=30°,
∵OE=OF,OH⊥BC,
∴EH=FH=1,
∴BE=CF=BH﹣EH=﹣1,
同理:AP2=BP1=BE=CF=CP4=DP3=﹣1,
①当∠EP1F=30°时,
在Rt△P1BE中,∵BP1=BE=﹣1,
∴P1E=BE=﹣;
②当∠EP2F=30°时,
在Rt△P2BE中,BP2=AB﹣AP2=+1,
则P2E==2;
③当∠EP3F=30°时,
在Rt△P3CE中,CP3=CE=+1,
∴P3E=CE=+;
④当∠EP4F=30°时,
在Rt△P4CE中,CP4=﹣1,CE=+1,
则P4E==2.
综上,PE=﹣或2或+.
故答案为:﹣或2或+.
13.解:如图,过点E作EF⊥AD于F,
∵∠BAD=∠EFD=90°,
∴EF∥AB,
∴∠BAP=∠AEF=∠BAE,
∵点P为BC中点,
∴BP=AB=1,
∴AP==,
∴==,
∴AE=,
∴EF=,
∴S△ADE=AD EF=×2×=;
如图,把△APB绕点A逆时针旋转90°得到△ADG,取AG的中点H,连接HD、HP,
由旋转的性质,得:AG=AP,∠1=∠2,∠ADG=∠ABP=90°,
∴∠2+∠3=∠1+∠3=90°,AH=HD=AP,
∵AH2+AP2=HP2,
∴HP=AP,
∵HD+DP≥HP,
∴AP+DP≥AP,
∴DP≥AP,
∴的最小值为.
故答案为:; .
14.解:如图:过E作EM⊥OC,垂足为M,
过点O作ON⊥BC,垂足为N,
过点F作FP⊥BC,垂足为G,设EM=x,
∴∠CME=∠CBP=90°,
∴CM=x,
又∵∠EOC=∠POF=45°,
∴OM=x,OE=x,
∴OC=OM+CM=x,CE==x,
∴正方形的边长为2CE=x,
∴AP=x,
在△COE中,S△COE=OC BM=ON EC,
解得:ON=x,
∴NE==x,
∵ON⊥BC,GF⊥BC,
∴ON∥FG,
∴EG=x,
∴BG=BE﹣EG=()x=x,
∵AB∥FPGAF∥BG,
∴四边形ABGF为矩形,
∴AF=BG=x,
∴S△APF=AP AF= x x=,
解得:x=,
∴EF=××=.
故答案为:.
15.解:如图,过C作CH⊥AE于H,
∵AG=GE,
∴AB=BE,
∴∠BAE=BEA,
∵BG⊥AE,
∴∠BGP=∠CHP=90°,
∵P为BC的中点,
∴BP=CP,
在△BGP和△CHP中,
,
∴△BGP≌△CHP(AAS),
∴BG=CH,∠GBP=∠PCH,
∵四边形ABCD是正方形,
∴AB=BC,
∴BC=BE,
∴∠BCE=∠BEC,
∵∠ABC=∠ABG+∠GBP=90°,∠ABG+∠BAG=90°,
∴∠GBP=∠BAG,
∴∠PCH=∠BEP,
∴∠HCE=∠HEC,
∴CH=EH,
∵∠CHE=90°,
∴CE=CH,即CE=BG,
在Rt△ABP中,AB=2,BP=BC=1,
∴AP==,
∵S△ABP=AB BP=AP BG,
∴BG==,
∴CE=×=,
故答案为.
16.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
17.(1)证明:在矩形ABCD中,有∠A=∠D=90°,
∴∠DGH+∠DHG=90°.
在菱形EFGH中,EH=GH
∵AH=2,DG=2,
∴AH=DG,
∴Rt△AEH≌Rt△DHG(HL).
∴∠AHE=∠DGH.
∴∠AHE+∠DHG=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
(2)过F作FM⊥DC于M,则∠FMG=90°.
∴∠A=∠FMG=90°.连接EG.
由矩形和菱形性质,知AB∥DC,HE∥GF,
∴∠AEG=∠MGE,∠HEG=∠FGE,
∴∠AEH=∠MGF.
∵EH=GF,
∴△AEH≌△MGF.
∴FM=AH=2.
∵S △FCG=,
∴CG=2.
18.解:作DE⊥BC,交BC延长线于E,如图,
∵DP⊥AB,ABC=90°,
∴四边形BEDP为矩形,
∴∠PDE=90°,即∠CDE+∠PDC=90°,
∵∠ADC=90°,即∠ADP+∠PDC=90°,
∴∠ADP=∠CDE,
在△ADP和△CDE中,
,
∴△ADP≌△CDE,
∴DP=DE,S△ADP=S△CDE,
∴四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,
∴DP2=36,
∴DP=6.
19.解:如图,过点B作BF⊥AD交DA的延长线于F,
∵AD∥BC,∠D=90°,BC=CD,
∴四边形BCDF是正方形,
把△BCE绕点B顺时针旋转90°得到△BFG,
则CE=FG,BE=BG,∠CBE=∠FBG,
∵∠ABE=45°,
∴∠ABG=∠ABF+∠FBG=∠ABF+∠CBE=90°﹣∠ABE=90°﹣45°=45°,
∴∠ABE=∠ABG,
在△ABE和△ABG中,
,
∴△ABE≌△ABG(SAS),
∴AE=AG,
∴AF+CE=AF+FG=AG=AE,
设CE=x,则DE=6﹣x,AF=5﹣x,
∴AD=6﹣(5﹣x)=x+1,
在Rt△ADE中,AD2+DE2=AE2,
即(x+1)2+(6﹣x)2=52,
整理得,x2﹣5x+6=0,
解得x1=2,x2=3,
所以CE的长度是2或3.
20.证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AF=BP=CQ=DE,
∴DF=CE=BQ=AP,
在△APF和△DFE和△CEQ和△BQP中,
,
∴△APF≌△DFE≌△CEQ≌△BQP(SAS),
∴EF=FP=PQ=QE;
(2)∵EF=FP=PQ=QE,
∴四边形EFPQ是菱形,
∵△APF≌△BQP,
∴∠AFP=∠BPQ,
∵∠AFP+∠APF=90°,
∴∠APF+∠BPQ=90°,
∴∠FPQ=90°,
∴四边形EFPQ是正方形.
