2021-2022学年鲁教版八年级数学下册6.2矩形的性质与判定 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册6.2矩形的性质与判定 同步练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 11:42:33 | ||
图片预览



文档简介
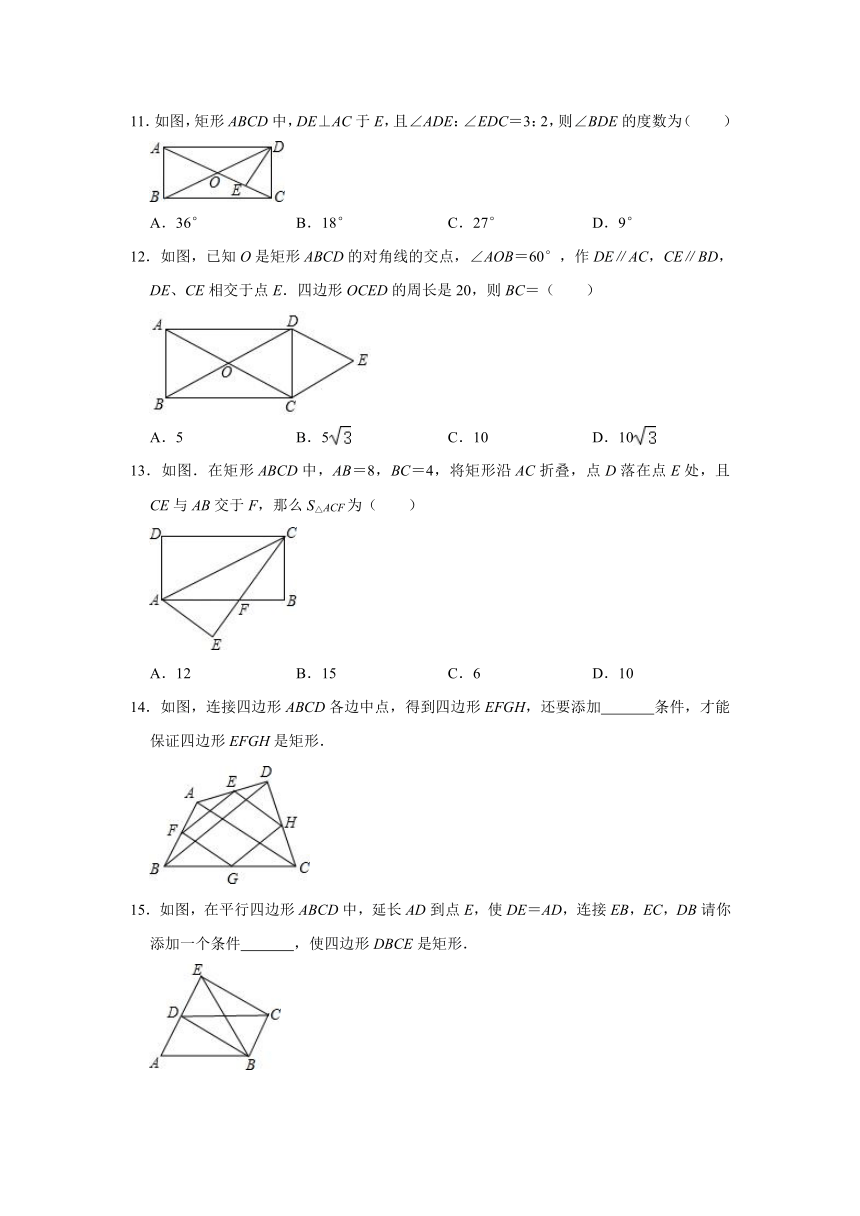
2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》同步练习题(附答案)
1.如图,在矩形ABCD中,M是BC上的动点,E,F分别是AM,MC的中点,则EF的长随着M点的运动( )
A.变短 B.变长
C.不变 D.先变短再变长
2.如图,在矩形ABCD中,AB=8厘米,BC=10厘米,点E在边AB上,且AE=2厘米,如果动点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,动点Q在线段CD上由C点向D点运动,设运动时间为t秒,当△BPE与△CQP全等时,t的值为( )
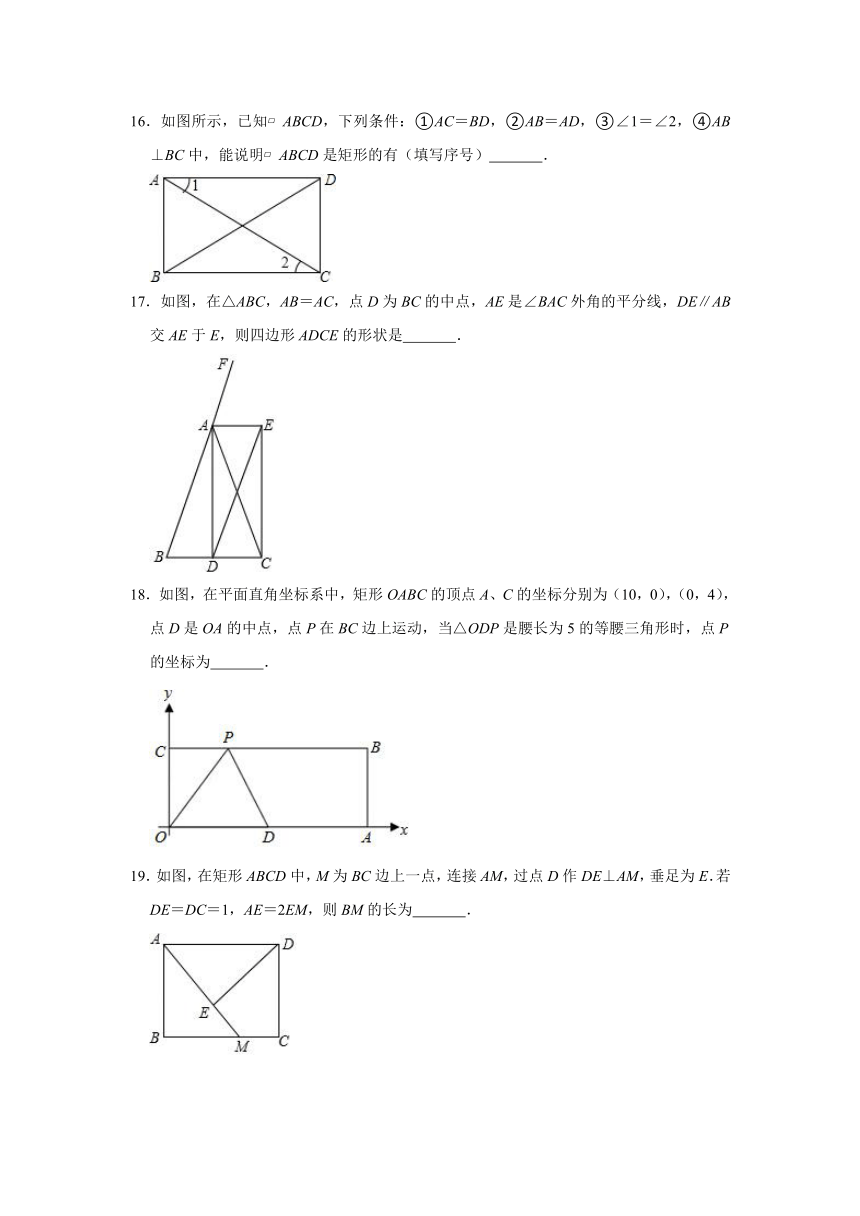
A.2 B.1.5或2 C.2.5 D.2或2.5
3.如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=3,OA=2,则AD的长为( )
A.5 B. C. D.
4.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB; ④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
5.如图,延长矩形ABCD的边BC至点E,使CE=CA,连接AE,如果∠ACB=38°,则∠E的值是( )
A.18° B.19° C.20° D.40°
6.菱形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对角互补
7.矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为( )
A.3cm2 B.4cm2 C.12cm2 D.4cm2或12cm2
8.如图,矩形ABCD中,∠AOB=60°,AB=2,则AC的长为( )
A.2 B.4 C.2 D.4
9.如图,在矩形COED中,点D的坐标是(1,2),则CE的长是( )
A. B.2 C. D.
10.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )
A.10 B.9.6 C.4.8 D.2.4
11.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A.36° B.18° C.27° D.9°
12.如图,已知O是矩形ABCD的对角线的交点,∠AOB=60°,作DE∥AC,CE∥BD,DE、CE相交于点E.四边形OCED的周长是20,则BC=( )
A.5 B.5 C.10 D.10
13.如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )
A.12 B.15 C.6 D.10
14.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加 条件,才能保证四边形EFGH是矩形.
15.如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件 ,使四边形DBCE是矩形.
16.如图所示,已知 ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明 ABCD是矩形的有(填写序号) .
17.如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE∥AB交AE于E,则四边形ADCE的形状是 .
18.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
19.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为 .
20.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
21.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
22.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
23.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
24.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD中点,连接OE.过点C作CF∥BD交OE的延长线于点F,连接DF.
求证:(1)△ODE≌△FCE;
(2)四边形OCFD是矩形.
25.如图,在 ABCD中,AE⊥BC于点E,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
26.如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
参考答案
1.解:∵E,F分别是AM,MC的中点,
∴EF=AC,
∵C是定点,
∴AC是定长,
∴无论M运动到哪个位置EF的长不变,
故选:C.
2.解:当点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=8厘米,BC=10厘米,AE=2厘米,
∴BE=CP=6厘米,
∴BP=10﹣6=4厘米,
∴运动时间=4÷2=2(秒);
当点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t==(秒),
故选:D.
3.解:∵矩形ABCD中,两条对角线AC与BD相交于点O,OA=2,
∴AC=2AO=4,
又∵AB=3,∠ABC=90°,
∴BC==,
∴AD=BC=,
故选:D.
4.解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°=∠ACB,
∴∠BOE=(180°﹣30°)=75°,BC=AB,故③错误;
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴S△AOE=S△COE,故⑤正确;
故选:B.
5.解:∵CE=CA,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=19°
故选:B.
6.解:A、菱形对角线相互垂直,而矩形的对角线则不垂直;故本选项符合要求;
B、矩形的对角线相等,而菱形的不具备这一性质;故本选项不符合要求;
C、菱形和矩形的对角线都互相平分;故本选项不符合要求;
D、菱形对角相等;但菱形不具备对角互补,故本选项不符合要求;
故选:A.
7.解:
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
①当AE=1cm时,AB=1cm=CD,AD=1cm+3cm=4cm=BC,
此时矩形的面积是1cm×4cm=4cm2;
②当AE=3cm时,AB=3cm=CD,AD=4cm=BC,
此时矩形的面积是:3cm×4cm=12cm2;
故选:D.
8.解:∵四边形ABCD是矩形,
∴AO=BO,
∵∠AOB=60°,
∴∠OAB=∠ABO=60°,
∴△ABO是等边三角形,
∵AB=2,
∴AO=BO=AB=2.
∴AC=2A0=4,
故选:B.
9.解:∵四边形COED是矩形,
∴CE=OD,
∵点D的坐标是(1,2),
∴OD=,
∴CE=,
故选:C.
10.解:连接OP,
∵矩形ABCD的两边AB=6,BC=8,
∴S矩形ABCD=AB BC=48,OA=OC,OB=OD,AC=BD,AC==10,
∴S△AOD=S矩形ABCD=12,OA=OD=5,
∴S△AOD=S△AOP+S△DOP=OA PE+OD PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF==4.8.
故选:C.
11.解:已知∠ADE:∠EDC=3:2 ∠ADE=54°,∠EDC=36°,
又因为DE⊥AC,所以∠DCE=90°﹣36°=54°,
根据矩形的性质可得∠DOC=180°﹣2×54°=72°
所以∠BDE=180°﹣∠DOC﹣∠DEO=18°
故选:B.
12.解:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,
∴OC=OD,
∴四边形OCED是菱形;
∵四边形OCED的周长是20,
∴CO=DO=5,
∴BD=10,
∵四边形ABCD是矩形,
∴OA=OB,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=OC=AB=5,
∴BC==5.
故选:B.
13.解:∵四边形ABCD是矩形,
∴∠B=90°,AB∥CD,
∴∠DCA=∠BAC,
∵矩形沿AC折叠,点D落在点E处,
∴△ACD≌△ACE,
∴∠DCA=∠ECA,
∴∠BAC=∠ECA,
∴AF=CF,
设AF=CF=x,则BF=8﹣x,
在Rt△BCF中,根据勾股定理得:BC2+BF2=CF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴AF=5,
∴S△ACF=AF BC=×5×4=10.
故选:D.
14.解:∵G、H、E分别是BC、CD、AD的中点,
∴HG∥BD,EH∥AC,
∴∠EHG=∠1,∠1=∠2,
∴∠2=∠EHG,
∵四边形EFGH是矩形,
∴∠EHG=90°,
∴∠2=90°,
∴AC⊥BD.
故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
15.解:添加EB=DC.理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴DE∥BC,
又∵DE=AD,
∴DE=BC,
∴四边形DBCE为平行四边形.
又∵EB=DC,
∴四边形DBCE是矩形.
故答案是:EB=DC.
16.解:能说明 ABCD是矩形的有:
①对角线相等的平行四边形是矩形;
④有一个角是直角的平行四边形是矩形.
17.证明:∵AB=AC,
∴∠B=∠ACB,
∵点D为BC的中点,
∴∠ADC=90°,
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE平行且等于BD,
又∵BD=DC,
∴AE平行且等于DC,
故四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
即四边形ADCE是矩形.
故答案为矩形.
18.解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE===3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4);
故答案为:(2,4)或(3,4)或(8,4);
19.解:∵四边形ABCD是矩形,
∴AB=DC=1,∠B=∠C=90°,AD∥BC,AD=BC,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
∴∠DEA=∠DEM=90°,
在△ABM和△DEA中,,
∴△ABM≌△DEA(AAS),
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
设EM=CM=x,则BM=2x,AM=BC=3x,
在Rt△ABM中,由勾股定理得:12+(2x)2=(3x)2,
解得:x=,
∴BM=;
故答案为:.
20.解:(1)∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)∵四边形ABCD是菱形,
∴BD⊥AC,AB=AD=10,
∴∠AOD=90°,
∵E是AD的中点,
∴OE=AE=AD=5;
由(1)知,四边形OEFG是矩形,
∴FG=OE=5,
∵AE=5,EF=4,
∴AF==3,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.
21.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=9﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
22.(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形.
(2)作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积= EC OF=1.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC==5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
24.证明:(1)∵CF∥BD,
∴∠ODE=∠FCE,
∵E是CD中点,
∴CE=DE,
在△ODE和△FCE中,,
∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,
∴OD=FC,
∵CF∥BD,
∴四边形OCFD是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴四边形OCFD是矩形.
25.(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.
∵AE⊥BF,
∴△ABF的面积=AB AF=BF AE.
∴AE===.
26.(1)证明:∵点O是AC中点,
∴AO=OC,
∵OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边BC上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)解:∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD===15,
∴四边形ADCE的面积是AD×DC=15×8=120.
1.如图,在矩形ABCD中,M是BC上的动点,E,F分别是AM,MC的中点,则EF的长随着M点的运动( )
A.变短 B.变长
C.不变 D.先变短再变长
2.如图,在矩形ABCD中,AB=8厘米,BC=10厘米,点E在边AB上,且AE=2厘米,如果动点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,动点Q在线段CD上由C点向D点运动,设运动时间为t秒,当△BPE与△CQP全等时,t的值为( )
A.2 B.1.5或2 C.2.5 D.2或2.5
3.如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=3,OA=2,则AD的长为( )
A.5 B. C. D.
4.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB; ④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
5.如图,延长矩形ABCD的边BC至点E,使CE=CA,连接AE,如果∠ACB=38°,则∠E的值是( )
A.18° B.19° C.20° D.40°
6.菱形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对角互补
7.矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为( )
A.3cm2 B.4cm2 C.12cm2 D.4cm2或12cm2
8.如图,矩形ABCD中,∠AOB=60°,AB=2,则AC的长为( )
A.2 B.4 C.2 D.4
9.如图,在矩形COED中,点D的坐标是(1,2),则CE的长是( )
A. B.2 C. D.
10.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )
A.10 B.9.6 C.4.8 D.2.4
11.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
A.36° B.18° C.27° D.9°
12.如图,已知O是矩形ABCD的对角线的交点,∠AOB=60°,作DE∥AC,CE∥BD,DE、CE相交于点E.四边形OCED的周长是20,则BC=( )
A.5 B.5 C.10 D.10
13.如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )
A.12 B.15 C.6 D.10
14.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加 条件,才能保证四边形EFGH是矩形.
15.如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件 ,使四边形DBCE是矩形.
16.如图所示,已知 ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明 ABCD是矩形的有(填写序号) .
17.如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE∥AB交AE于E,则四边形ADCE的形状是 .
18.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
19.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为 .
20.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
21.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
22.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
23.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
24.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD中点,连接OE.过点C作CF∥BD交OE的延长线于点F,连接DF.
求证:(1)△ODE≌△FCE;
(2)四边形OCFD是矩形.
25.如图,在 ABCD中,AE⊥BC于点E,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
26.如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.
参考答案
1.解:∵E,F分别是AM,MC的中点,
∴EF=AC,
∵C是定点,
∴AC是定长,
∴无论M运动到哪个位置EF的长不变,
故选:C.
2.解:当点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=8厘米,BC=10厘米,AE=2厘米,
∴BE=CP=6厘米,
∴BP=10﹣6=4厘米,
∴运动时间=4÷2=2(秒);
当点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t==(秒),
故选:D.
3.解:∵矩形ABCD中,两条对角线AC与BD相交于点O,OA=2,
∴AC=2AO=4,
又∵AB=3,∠ABC=90°,
∴BC==,
∴AD=BC=,
故选:D.
4.解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°=∠ACB,
∴∠BOE=(180°﹣30°)=75°,BC=AB,故③错误;
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴S△AOE=S△COE,故⑤正确;
故选:B.
5.解:∵CE=CA,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=19°
故选:B.
6.解:A、菱形对角线相互垂直,而矩形的对角线则不垂直;故本选项符合要求;
B、矩形的对角线相等,而菱形的不具备这一性质;故本选项不符合要求;
C、菱形和矩形的对角线都互相平分;故本选项不符合要求;
D、菱形对角相等;但菱形不具备对角互补,故本选项不符合要求;
故选:A.
7.解:
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
①当AE=1cm时,AB=1cm=CD,AD=1cm+3cm=4cm=BC,
此时矩形的面积是1cm×4cm=4cm2;
②当AE=3cm时,AB=3cm=CD,AD=4cm=BC,
此时矩形的面积是:3cm×4cm=12cm2;
故选:D.
8.解:∵四边形ABCD是矩形,
∴AO=BO,
∵∠AOB=60°,
∴∠OAB=∠ABO=60°,
∴△ABO是等边三角形,
∵AB=2,
∴AO=BO=AB=2.
∴AC=2A0=4,
故选:B.
9.解:∵四边形COED是矩形,
∴CE=OD,
∵点D的坐标是(1,2),
∴OD=,
∴CE=,
故选:C.
10.解:连接OP,
∵矩形ABCD的两边AB=6,BC=8,
∴S矩形ABCD=AB BC=48,OA=OC,OB=OD,AC=BD,AC==10,
∴S△AOD=S矩形ABCD=12,OA=OD=5,
∴S△AOD=S△AOP+S△DOP=OA PE+OD PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF==4.8.
故选:C.
11.解:已知∠ADE:∠EDC=3:2 ∠ADE=54°,∠EDC=36°,
又因为DE⊥AC,所以∠DCE=90°﹣36°=54°,
根据矩形的性质可得∠DOC=180°﹣2×54°=72°
所以∠BDE=180°﹣∠DOC﹣∠DEO=18°
故选:B.
12.解:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,
∴OC=OD,
∴四边形OCED是菱形;
∵四边形OCED的周长是20,
∴CO=DO=5,
∴BD=10,
∵四边形ABCD是矩形,
∴OA=OB,
又∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=OC=AB=5,
∴BC==5.
故选:B.
13.解:∵四边形ABCD是矩形,
∴∠B=90°,AB∥CD,
∴∠DCA=∠BAC,
∵矩形沿AC折叠,点D落在点E处,
∴△ACD≌△ACE,
∴∠DCA=∠ECA,
∴∠BAC=∠ECA,
∴AF=CF,
设AF=CF=x,则BF=8﹣x,
在Rt△BCF中,根据勾股定理得:BC2+BF2=CF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴AF=5,
∴S△ACF=AF BC=×5×4=10.
故选:D.
14.解:∵G、H、E分别是BC、CD、AD的中点,
∴HG∥BD,EH∥AC,
∴∠EHG=∠1,∠1=∠2,
∴∠2=∠EHG,
∵四边形EFGH是矩形,
∴∠EHG=90°,
∴∠2=90°,
∴AC⊥BD.
故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
15.解:添加EB=DC.理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴DE∥BC,
又∵DE=AD,
∴DE=BC,
∴四边形DBCE为平行四边形.
又∵EB=DC,
∴四边形DBCE是矩形.
故答案是:EB=DC.
16.解:能说明 ABCD是矩形的有:
①对角线相等的平行四边形是矩形;
④有一个角是直角的平行四边形是矩形.
17.证明:∵AB=AC,
∴∠B=∠ACB,
∵点D为BC的中点,
∴∠ADC=90°,
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE平行且等于BD,
又∵BD=DC,
∴AE平行且等于DC,
故四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
即四边形ADCE是矩形.
故答案为矩形.
18.解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE===3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4);
故答案为:(2,4)或(3,4)或(8,4);
19.解:∵四边形ABCD是矩形,
∴AB=DC=1,∠B=∠C=90°,AD∥BC,AD=BC,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
∴∠DEA=∠DEM=90°,
在△ABM和△DEA中,,
∴△ABM≌△DEA(AAS),
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
设EM=CM=x,则BM=2x,AM=BC=3x,
在Rt△ABM中,由勾股定理得:12+(2x)2=(3x)2,
解得:x=,
∴BM=;
故答案为:.
20.解:(1)∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)∵四边形ABCD是菱形,
∴BD⊥AC,AB=AD=10,
∴∠AOD=90°,
∵E是AD的中点,
∴OE=AE=AD=5;
由(1)知,四边形OEFG是矩形,
∴FG=OE=5,
∵AE=5,EF=4,
∴AF==3,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2.
21.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=9﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
22.(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形.
(2)作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积= EC OF=1.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC==5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
24.证明:(1)∵CF∥BD,
∴∠ODE=∠FCE,
∵E是CD中点,
∴CE=DE,
在△ODE和△FCE中,,
∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,
∴OD=FC,
∵CF∥BD,
∴四边形OCFD是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴四边形OCFD是矩形.
25.(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
∵在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.
∵AE⊥BF,
∴△ABF的面积=AB AF=BF AE.
∴AE===.
26.(1)证明:∵点O是AC中点,
∴AO=OC,
∵OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边BC上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)解:∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD===15,
∴四边形ADCE的面积是AD×DC=15×8=120.
