2021-2022学年鲁教版八年级数学下册6.1菱形的性质与判定 解答题专题训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册6.1菱形的性质与判定 解答题专题训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 567.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 11:51:12 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《6-1菱形的性质与判定》解答题专题训练(附答案)
1.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若∠C=90°,BC=16,CD=8,求菱形BNDM的周长.
2.如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,AC=2AB,BE∥AC,OE∥AB.
(1)求证:四边形ABEO是菱形;
(2)若AC=2,BD=4,求四边形ABEO的面积.
如图1,在 ABCD中,AB=AD,AC=16,BD=12,AC、BD相交于点O.
(1)求AB的长.
(2)若CE∥BD,BE∥AC,连接OE,求证:OE=AD.
(3)如图2,设BC与OE相交于点P,连接DP,求DP的长.
4.如图,四边形ABCD的对角线AC⊥BD于点E.点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.
(1)求证:四边形DBFC是菱形;
(2)若AB=BC,∠F=45°,BD=2,则AC= .
5.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠BDE=15°,∠C=45°,CD=2,求DE的长.
6.在Rt△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明:四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
7.如图,△ABC中,AB=AC=2,∠BAC=30°,△ADF≌△ABC,AD⊥AC,连接BD、CF交于点E.
(1)求证:四边形ABEF为菱形;
(2)求CE的长.
8.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
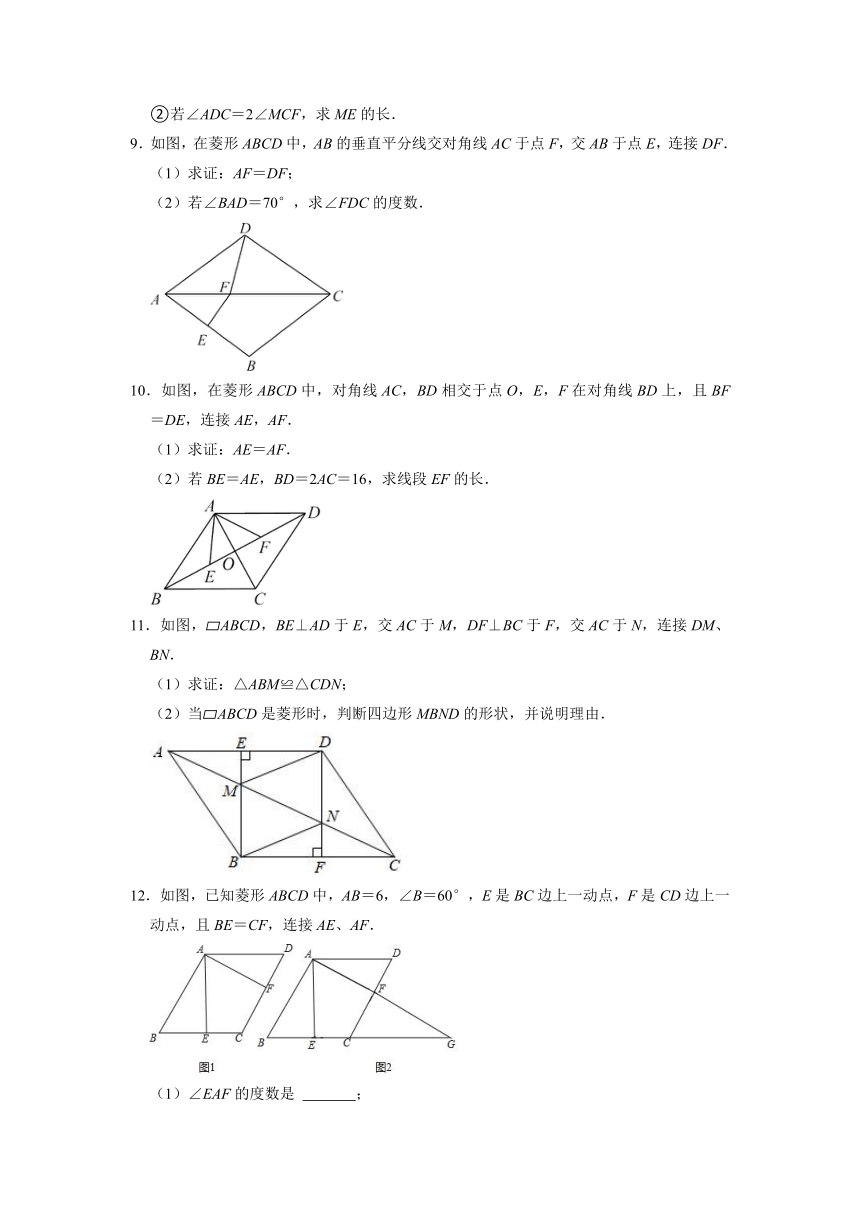
9.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF.
(1)求证:AF=DF;
(2)若∠BAD=70°,求∠FDC的度数.
10.如图,在菱形ABCD中,对角线AC,BD相交于点O,E,F在对角线BD上,且BF=DE,连接AE,AF.
(1)求证:AE=AF.
(2)若BE=AE,BD=2AC=16,求线段EF的长.
11.如图, ABCD,BE⊥AD于E,交AC于M,DF⊥BC于F,交AC于N,连接DM、BN.
(1)求证:△ABM≌△CDN;
(2)当 ABCD是菱形时,判断四边形MBND的形状,并说明理由.
12.如图,已知菱形ABCD中,AB=6,∠B=60°,E是BC边上一动点,F是CD边上一动点,且BE=CF,连接AE、AF.
(1)∠EAF的度数是 ;
(2)求证:AE=AF;
(3)延长AF交BC的延长线于点G,当∠BAE=30°时,求点F到BG的距离
13.如图,在菱形ABCD中,∠BAD=45°,对角线AC与BD相交于点O,DE⊥AB于点E,交AC于点F.
(1)求证:△AEF≌△DEB;
(2)若DE+EF=10,求菱形ABCD的周长.
14.如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,BE=4,求DG的值.
15.如图,在 ABCD中,点E、F为对角线BD的三等分点,连接AE,CF,AF,CE.
(1)求证:四边形AECF为平行四边形;
(2)若四边形AECF为菱形,且AE=BE,求∠BAD的度数.
16.如图,E,F分别是菱形ABCD的边AD,CD的中点,且AB=5,BD=6.
(1)求线段EF的长;
(2)探究四边形DEOF是什么特殊四边形?并对结论给予证明.
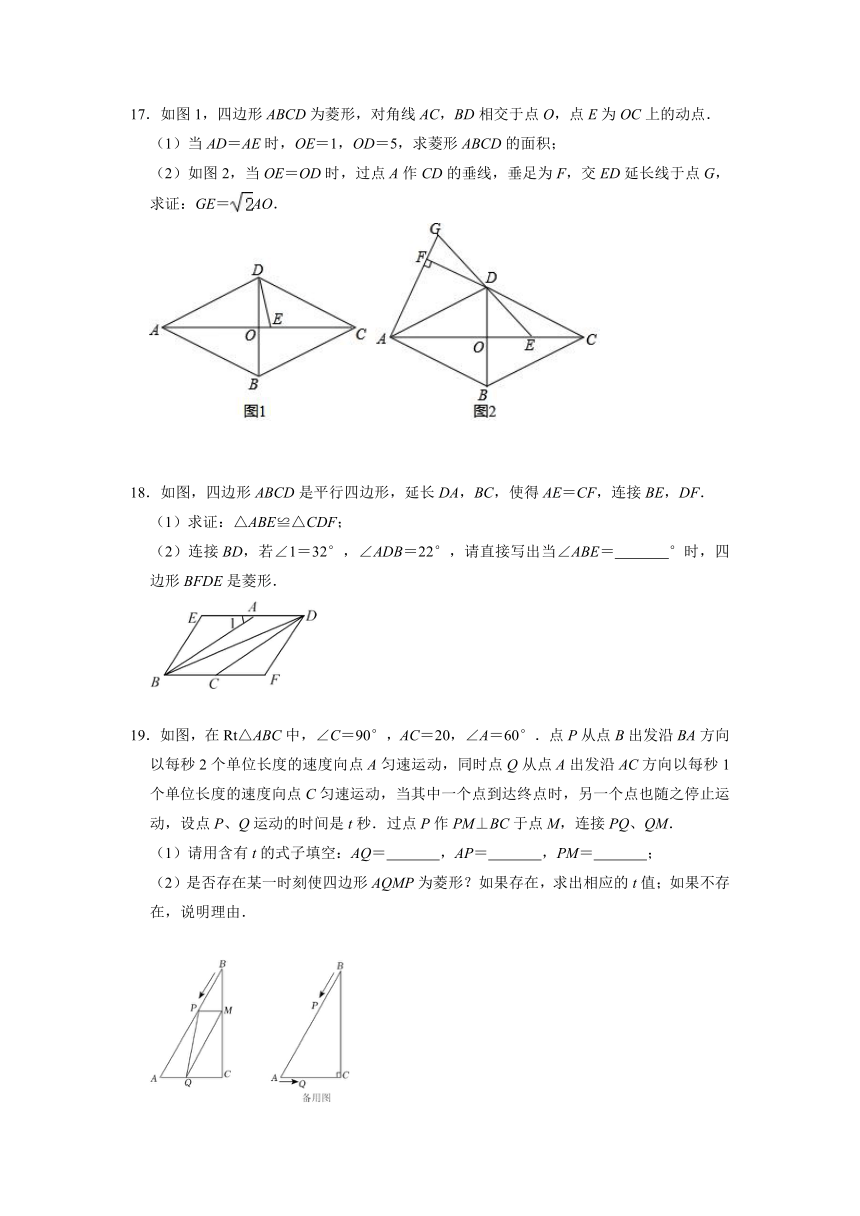
17.如图1,四边形ABCD为菱形,对角线AC,BD相交于点O,点E为OC上的动点.
(1)当AD=AE时,OE=1,OD=5,求菱形ABCD的面积;
(2)如图2,当OE=OD时,过点A作CD的垂线,垂足为F,交ED延长线于点G,求证:GE=AO.
18.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
19.如图,在Rt△ABC中,∠C=90°,AC=20,∠A=60°.点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动,同时点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点P、Q运动的时间是t秒.过点P作PM⊥BC于点M,连接PQ、QM.
(1)请用含有t的式子填空:AQ= ,AP= ,PM= ;
(2)是否存在某一时刻使四边形AQMP为菱形?如果存在,求出相应的t值;如果不存在,说明理由.
20.如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)当∠B为多少度时,四边形AEGF为菱形,请说明理由.
21.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP,BQ,PQ.
(1)求证:AP=BQ;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.
22.已知:平行四边形ABCD,对角线AC,BD相交于点O.E是AD的中点,连接OE并延长至F使得OE=EF,连接FD,FC,FC交BD于点G.
求证:(1)△FGD≌△CGO;
(2)当AB与AC有怎样的数量关系时,四边形FOCD是菱形,并说明理由.
23.如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE;
(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.
24.如图,在四边形ABCD中,AC是BD的垂直平分线,E是CD上一点,BE交AC于F,连接DF.∠BEC=∠ADF,试证明四边形ABCD是菱形.
25.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.求证:四边形AEDF是菱形.
26.在 ABCD中,对角线AC、BD交于点O,E是边BC延长线上的动点,过点E作EF⊥BD于F,且与CD、AD分别交于点G、H,连接OH.
(1)如图,若AC⊥AB,OF=OC,求证:FG=CG;
(2)若在点E运动的过程中,存在四边形OCGH是菱形的情形,试探究 ABCD的边和角需要满足的条件.
27.已知:如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别是
E,F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)求证:四边形ABCD是菱形.
28.如图,点E、F分别在 ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,求证:四边形AECF是菱形.
29.如图,已知BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,垂足分别为E、D,联结CD、DE,DE与AB交于点O,CD∥AB.求证:四边形OBCD是菱形.
30.如图,在平行四边形ABCD中,E,F是对角线BD上的点,且BE=DF,连接AE,CF.
(1)求证△ADE≌△CBF;
(2)连接AF,CE,若AB=AD,求证:四边形AFCE是菱形.
参考答案
1.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:∵四边形BNDM是菱形,
∴BM=BN=DM=DN,
设BN=DN=x,则CN=BC﹣BN=16﹣x,
在Rt△CDN中,由勾股定理得:CD2+CN2=DN2,
即82+(16﹣x)2=x2,
解得:x=10,
即BN=10,
∴菱形BNDM的周长=4BN=40.
2.证明:(1)∵BE∥AC,OE∥AB,
∴四边形ABEO是平行四边形,
∵四边形ABCD是平行四边形,
∴AC=2AO,
∵AC=2AB,
∴AO=AB,
∴四边形ABEO是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AO=AC=,OB=BD=2,
连接AE交BO于M,
由(1)知,四边形ABEO是菱形,
∴AE、OB互相垂直平分,
∴OM=BO=1,
∴AM=,
∴AE=4,
∴四边形ABEO的面积=AE OB=.
3.(1)解:∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形,
∴OA=OC=AC=8,OB=OD=BD=6,AC⊥BD,
∴∠AOB=90°,
∴AB===10;
(2)证明:∵CE∥BD,BE∥AC,
∴四边形OBEC是平行四边形,
由(1)得:四边形ABCD是菱形,
∴AD=BC,AC⊥BD,
∴∠BOC=90°,
∴平行四边形OBEC是矩形,
∴OE=BC,
∴OE=AD;
(3)解:过D作DH⊥BC于H,如图2所示:
∵四边形ABCD是菱形,
∴BC=AB=10,菱形ABCD的面积=BC×DH=AC×BD,
即10DH=×16×12,
∴DH=,
在Rt△BDH中,由勾股定理得:BH===,
由(2)得:四边形OBEC是矩形,
∴PB=PC,
∵∠BOC=90°,
∴PB=BC=5,
∴PH=BH﹣PB=﹣5=,
在Rt△PDH中,DP===.
4.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴平行四边形DBFC是菱形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
过C作CM⊥BF于M,如图所示:
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=CM=,
∴AC=2AE=2,
故答案为:2.
5.(1)证明:∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠EDB,
∴BE=DE,
∴平行四边形BEDF是菱形;
(2)解:过点D作DH⊥BC于点H,如图所示:
∵四边形BEDF是菱形,
∴BF=DF=DE,
∴∠FBD=∠FDB=∠BDE=15°,
∴∠DFH=30°,
∵DH⊥BC,
∴∠DHF=∠DHC=90°,
∴DH=DF,
∵∠C=45°,
∴△CDH是等腰直角三角形,
∴DH=CH=CD=×2=2,
∴DF=2DH=4,
∴DE=4.
6.(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
∴AF=DB,
又∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,
∴平行四边形ADCF是菱形;
(2)解:∵D是BC的中点,
∴△ACD的面积=△ABD的面积=△ABC的面积,
∵四边形ADCF是菱形,
∴菱形ADCF的面积=2△ACD的面积=△ABC的面积=AC×AB=×4×5=10.
7.证明:(1)∵△ADF≌△ABC,
∴AB=AD=AF=AC,BC=DF,∠BAC=∠DAF=30°,
∴∠BAD=∠CAF=120°,
∴∠ABD=∠ADB=30°,∠ACF=∠AFC=30°,
∴∠DAF=∠ADB=30°,∠ACF=∠BAC=30°,
∴AF∥BD,AB∥CF,
∴四边形ABEF平行四边形,
又∵AB=AF,
∴四边形ABEF是菱形;
(2)如图,过点A作AH⊥CF于H,
∵AC=AF,∠AFC=30°,AH⊥CF,
∴CH=FH,AH=AF=1,
∴FH===,
∴CF=2,
∵四边形ABEF是菱形,
∴EF=AF=2,
∴CE=2﹣2.
8.(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠FDM=∠MDC,
∵ME⊥AC,AM=ME,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
9.(1)证明:连接BF,如图所示:∵EF是线段AB的垂直平分线,
∴AF=BF,
∵四边形ABCD是菱形,
∴BC=DC,∠BCF=∠DCF,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴BF=DF,
∴AF=DF;
(2)解:由(1)得:△BCF≌△DCF,
∴∠FDC=∠FBC,
∵四边形ABCD是菱形,
∴AB=BC,∠BAC=∠BAD=×70°=35°,AD∥BC,
∴∠BCF=∠DCF=∠BAC,∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,
∴∠FBA=∠BAC=35°,
∴∠FBC=∠ABC﹣∠ABF=110°﹣35°=75°,
∴∠FDC=∠FBC=75°.
10.(1)证明:四边形ABCD是菱形,
∴OB=OD,AC⊥BD,
∵BF=DE,
∴BF﹣OB=DE﹣OD,
∴OF=OE,
∴AE=AF;
(2)解:∵四边形ABCD是菱形,
∴OB=OD,AC⊥BD,OA=OC,
∵BD=2AC=16,
∴OA=4,OB=8,
设BE=AE=x,则OE=OB﹣BE=8﹣x,
在Rt△AOE中,AE2=OA2+OE2,
∴x2=(8﹣x)2+42,
解得x=5,
∴OE=8﹣5=3,
由(1)知OF=OE,
∴EF=2OE=6.
11.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠DAB=∠DCB,
∴∠BAC=∠DCA,
∵BE⊥AD,DF⊥BC,
∴∠DAB+∠ABM=90°,∠DCB+∠CDN=90°,
又∵∠DAB=∠DCB,
∴∠ABM=∠CDN,
在△ABM和△CDN中,
,
∴△ABM≌△CDN(ASA);
(2)解:四边形MBND是菱形,理由如下:
∵BE⊥AD,DF⊥BC,AD∥BC,
∴BE∥DF,
由(1)知△ABM≌△CDN,
∴BM=DN,
∴四边形MBND是平行四边形,
连接BD,如图所示:
∵四边形ABCD是菱形,
∴AC⊥BD,
即MN⊥BD,
∴平行四边形MBND是菱形.
12.解:(1)连接AC,
∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是正三角形,
∴AB=AC,∠ACB=60°,
∴∠ACF=∠ACB=60°,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴∠BAE=∠CAF,
∴∠EAF=∠EAC+∠CAF=∠EAC+∠BAE=60°,
故答案为60°;
(2)由(1)可知,△ABE≌△ACF,
∴AE=AF,
(3)当∠BAE=30°时,
∵∠B=60°,
∴∠AEB=90°,
∵∴△ABC是正三角形,
∴E为BC中点,
∴F为CD中点,
在Rt△ABE中,AB=6,BE=3,
∴AE==3,
过点F作FH⊥CG于点H,
∵F为CD中点,FH∥AE,
∴FH为△AEG中位线,
∴FH==,
∴点F到BG的距离.
13.(1)证明:∵DE⊥AB,
∴∠AED=∠DEB=90°,
∵∠BAD=45°,
∴∠ADE=∠BAD=45°,
∴AE=DE,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠OAB+∠ABD=∠BDE+∠ABD=90°,
∴∠OAB=∠BDE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(ASA);
(2)解:由(1)知,△AEF≌△DEB,
∴EF=EB,
∴AB=AE+EB=DE+EF=10,
∵四边形ABCD是菱形,
∴菱形ABCD的周长=4AB=4×10=40.
14.(1)证明:∵四边形ABCD是菱形,
∴CB=CD,
∵BE⊥CD于点E,DF⊥BC于点F,
∴∠BEC=∠DFC=90°,
在△BEC与△DFC中,
,
∴△BEC≌△DFC(AAS),
∴EC=FC,
∴BF=DE;
(2)解:∵∠A=45°,四边形ABCD是菱形,
∴∠C=∠A=45°,AG∥BC,AB=BC,
∴∠CBG=∠G=45°,
∴△DEG与△BEC是等腰直角三角形,
∵BE=CE=4,
∴AB=BC=AD=4,
∵∠A=∠G=45°,
∴∠ABG=90°,
∴AG=8,
∴DG=AG﹣AD=8﹣4.
15.证明:(1)∵四边形AECF是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵点E、F为对角线BD的三等分点,
∴BE=EF=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=AF=CF=CE,
又∵AE=BE,
∴AE=BE=EF=AF=DF,
∴∠EAB=∠EBA,∠EAF=∠EFA,∠FAD=∠FDA,△AEF是等边三角形,
∴∠EAF=∠AFE=∠AEF=60°,
∴∠BAE=30°,∠FAD=30°,
∴∠BAD=120°.
16.(1)证明:∵四边形ABCD是菱形,
∴OA=AC,OB=OD=BD=3,AC⊥BD,
∴∠AOB=90°,
∴OA===4,
∴AC=2OA=8,
∵E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴EF=BD=4,
(2)四边形DEOF是菱形.理由如下:
∵四边形ABCD是菱形,
∴DA=DC,OA=OC,OB=OD,
∴O是AC,BD的中点,
∵E,F分别是菱形ABCD的边AD,CD的中点,
∴DE=DA,DF=DC,OE,OF分别是△ACD和△CDA的中位线,
∴DE=DF,OE∥FD,OF∥DE,
∴四边形DEOF平行四边形,
∵DE=DF,
∴四边形DEOF是菱形.
17.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,BD=2DO=10,
∵AD=AE,
∴AD=AE=AO+OE=1+OA,
∵AD2=OD2+AO2,
∴(1+OA)2=25+AO2,
∴AO=12,
∴AC=24,
∴菱形ABCD的面积==120;
(2)如图,过点G作GH⊥AC于H,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,AD=CD,∠DAC=∠DCA,
∵OE=OD,
∴∠DEO=∠EDO=45°,
∵GH⊥AC,
∴∠HED=∠HGE=45°,
∴GH=HE,GE=GH,
设∠DAC=∠DCA=x,
∴∠EDC=45°﹣x=∠GDF,
∵AF⊥CF,
∴∠FGD=90°﹣∠GDF=45°+x,
∵∠DAF=90°﹣2x,
∴∠ADC=180°﹣∠GAD﹣∠AGD=45°+x,
∴∠ADC=∠AGD,
∴AG=AD,
在△AHG和△DOA中,
,
∴△AHG≌△DOA(AAS),
∴GH=AO,
∴GE=GH=AO.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
19.解:(1)∵点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动,
∴AQ=t,
∵∠C=90°,AC=20,∠A=60°,
∴∠B=30°,
∴AB=2AC=40,
∴AP=AB﹣BP=40﹣2t,
∵PM⊥BC,
∴∠PMB=90°,
∴PM=PB=t.
故答案为:t,40﹣2t,t;
(2)存在,理由如下:
由(1)知:AQ=PM,
∵AC⊥BC,PM⊥BC,
∴AQ∥PM,
∴四边形AQMP是平行四边形,
当AP=AQ时,平行四边形AQMP是菱形,
即40﹣2t=t,
解得t=,
则存在t=,使得平行四边形AQMP成为菱形.
20.(1)证明:∵AF=FG,
∴∠FAG=∠FGA,
∵AG 平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,∠CGE=∠GED,
∴∠C=90°,
∵F是AD的中点,FG∥AE,
∴FH是△ADE的中位线,
∴H是ED的中点
∴FG是线段ED的垂直平分线,
∴GE=GD,∠DHG=90°,
∴∠GDE=∠GED,
∴∠CGE=∠GDE,
在△ECG和△GHD中,
,
∴△ECG≌△GHD(AAS);
(2)解:当∠B为30°,四边形AEGF为菱形,理由如下:
由(1)得:DE∥BC,
∴∠ADE=∠B=30°,
∴AE=AD,
∴AE=AF=FG,
由(1)得:AE∥FG,
∴四边形AEGF是平行四边形,
∵AE=AF,
∴四边形AEGF是菱形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠DBC,
∵CQ∥DB,
∴∠BCQ=∠DBC,
∴∠ADB=∠BCQ
∵DP=CQ,
∴△ADP≌△BCQ(SAS),
∴AP=BQ;
(2)∵CQ∥DB,且CQ=DP,
∴四边形CQPD是平行四边形,
∴CD=PQ,CD∥PQ,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AB=PQ,AB∥PQ,
∴四边形ABQP是平行四边形,
∵△ADP≌△BCQ,
∴∠APD=∠BQC,
∵∠APD+∠APB=180°,∠ABP+∠BQC=180°,
∴∠ABP=∠APB,
∴AB=AP,
∴四边形ABQP是菱形.
22.(1)证明:在△ACD中,点O,E分别为边AC,AD中点,
∴OE为△ACD的中位线,
∴OE∥CD,,
又∵,
∴OF∥CD,OF=CD,
∴四边形OCDF为平行四边形,
∴FD∥OC,FD=OC,
∴∠GFD=∠GCO,∠GDF=∠GOC,
∴△FGD≌△HGO(ASA);
(2)解:当时,四边形FOCD是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OC=AC,
∵AB=AC,
∴AB=CD=OC,
由(1)得:四边形OCDF为平行四边形,
∴平行四边形FOCD是菱形,
23.(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF,
在△FCE和△BOE中,
,
∴△FCE≌△BOE(AAS);
(2)解:当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD,
∴四边形OCFD为菱形.
24.证明:∵AC是BD的垂直平分线,
∴AB=AD,BC=CD,
∴∠ABD=∠ADB,
∴∠BAF=∠DAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(SAS),
∴∠ABF=∠ADF,
∵∠BEC=∠ADF,
∴∠BEC=∠ABF,
∴AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,BC=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形.
25.证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠C,AD∥BC,AB∥CD,
∵AF∥ED,
∴四边形AEDF是平行四边形,
∵AD∥BC,
∴∠DGC=∠ADE,
∵DG=DC,
∴∠DGC=∠C,
∴∠BAD=∠ADE,
∴AE=DE,
∴平行四边形AEDF是菱形.
26.(1)证明:连接OG,如图1所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AC⊥AB,
∴AC⊥CD,
∴∠OCG=90°,
∵EF⊥BD,
∴∠OFG=90°,
在Rt△OFG和Rt△OCG中,
,
∴Rt△OFG≌Rt△OCG(HL),
∴FG=CG;
(2)解:如图2所示:
若四边形OCGH是菱形,
则OH=OC,OH∥CG,OC∥GH,
∵EF⊥BD,
∴AC⊥BD,
∴ ABCD是菱形,
∴CD=AD,OA=OC,
∴OA=OH,
∴∠OAH=∠OHA,
∵OH∥CG,
∴∠OHA=∠ADC,
∵CD=AD,
∴∠CAD=∠DCA,
∴∠CAD=∠ADC=∠DCA,
∴△ACD是等边三角形,
∴∠ADC=60°,
即要使四边形OCGH是菱形, ABCD的边和角需要满足的条件是:CD=AD,∠ADC=60°.
27.证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA);
(2)由(1)得:△ABE≌△ADF,
∴AB=AD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.
28.证明:(1)∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
又∵BE=DF,
∴AB+BE=DC+DF,
即AE=CF,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
∴AC、EF互相平分;
(2)∵AB∥DC,
∴∠AEO=∠CFO,
∵EF平分∠AEC,
∴∠AEO=∠CEO,
∴∠CEO=∠CFO
∴CE=CF,
由(1)可知,四边形AECF是平行四边形,
∴平行四边形AECF是菱形.
29.证明:∵BD、BE分别是∠ABC与∠ABF的平分线,
∴∠ABD+∠ABE=×180°=90°,
即∠EBD=90°,
又∵AE⊥BE,AD⊥BD,E、D是垂足,
∴∠AEB=∠ADB=90°,
∴四边形AEBD是矩形.
∴OB=OD,
∴∠OBD=∠ODB,
∵BD平分∠ABC,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∵CD∥AB,
∴四边形OBCD是平行四边形,
∵OB=OD,
∴平行四边形OBCD是菱形.
30.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
∵BE=DF,
∴BF=DE,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)连接AC,交BD于点O,
∵AB=AD,四边形ABCD是平行四边形,
∴四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形,
又∵AC⊥BD,
∴四边形AECF是菱形.
1.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若∠C=90°,BC=16,CD=8,求菱形BNDM的周长.
2.如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,AC=2AB,BE∥AC,OE∥AB.
(1)求证:四边形ABEO是菱形;
(2)若AC=2,BD=4,求四边形ABEO的面积.
如图1,在 ABCD中,AB=AD,AC=16,BD=12,AC、BD相交于点O.
(1)求AB的长.
(2)若CE∥BD,BE∥AC,连接OE,求证:OE=AD.
(3)如图2,设BC与OE相交于点P,连接DP,求DP的长.
4.如图,四边形ABCD的对角线AC⊥BD于点E.点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.
(1)求证:四边形DBFC是菱形;
(2)若AB=BC,∠F=45°,BD=2,则AC= .
5.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠BDE=15°,∠C=45°,CD=2,求DE的长.
6.在Rt△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明:四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
7.如图,△ABC中,AB=AC=2,∠BAC=30°,△ADF≌△ABC,AD⊥AC,连接BD、CF交于点E.
(1)求证:四边形ABEF为菱形;
(2)求CE的长.
8.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.
(1)求证:AM=AE;
(2)连接CM,DF=2.
①求菱形ABCD的周长;
②若∠ADC=2∠MCF,求ME的长.
9.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF.
(1)求证:AF=DF;
(2)若∠BAD=70°,求∠FDC的度数.
10.如图,在菱形ABCD中,对角线AC,BD相交于点O,E,F在对角线BD上,且BF=DE,连接AE,AF.
(1)求证:AE=AF.
(2)若BE=AE,BD=2AC=16,求线段EF的长.
11.如图, ABCD,BE⊥AD于E,交AC于M,DF⊥BC于F,交AC于N,连接DM、BN.
(1)求证:△ABM≌△CDN;
(2)当 ABCD是菱形时,判断四边形MBND的形状,并说明理由.
12.如图,已知菱形ABCD中,AB=6,∠B=60°,E是BC边上一动点,F是CD边上一动点,且BE=CF,连接AE、AF.
(1)∠EAF的度数是 ;
(2)求证:AE=AF;
(3)延长AF交BC的延长线于点G,当∠BAE=30°时,求点F到BG的距离
13.如图,在菱形ABCD中,∠BAD=45°,对角线AC与BD相交于点O,DE⊥AB于点E,交AC于点F.
(1)求证:△AEF≌△DEB;
(2)若DE+EF=10,求菱形ABCD的周长.
14.如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,BE=4,求DG的值.
15.如图,在 ABCD中,点E、F为对角线BD的三等分点,连接AE,CF,AF,CE.
(1)求证:四边形AECF为平行四边形;
(2)若四边形AECF为菱形,且AE=BE,求∠BAD的度数.
16.如图,E,F分别是菱形ABCD的边AD,CD的中点,且AB=5,BD=6.
(1)求线段EF的长;
(2)探究四边形DEOF是什么特殊四边形?并对结论给予证明.
17.如图1,四边形ABCD为菱形,对角线AC,BD相交于点O,点E为OC上的动点.
(1)当AD=AE时,OE=1,OD=5,求菱形ABCD的面积;
(2)如图2,当OE=OD时,过点A作CD的垂线,垂足为F,交ED延长线于点G,求证:GE=AO.
18.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
19.如图,在Rt△ABC中,∠C=90°,AC=20,∠A=60°.点P从点B出发沿BA方向以每秒2个单位长度的速度向点A匀速运动,同时点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点P、Q运动的时间是t秒.过点P作PM⊥BC于点M,连接PQ、QM.
(1)请用含有t的式子填空:AQ= ,AP= ,PM= ;
(2)是否存在某一时刻使四边形AQMP为菱形?如果存在,求出相应的t值;如果不存在,说明理由.
20.如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)当∠B为多少度时,四边形AEGF为菱形,请说明理由.
21.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP,BQ,PQ.
(1)求证:AP=BQ;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.
22.已知:平行四边形ABCD,对角线AC,BD相交于点O.E是AD的中点,连接OE并延长至F使得OE=EF,连接FD,FC,FC交BD于点G.
求证:(1)△FGD≌△CGO;
(2)当AB与AC有怎样的数量关系时,四边形FOCD是菱形,并说明理由.
23.如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE;
(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.
24.如图,在四边形ABCD中,AC是BD的垂直平分线,E是CD上一点,BE交AC于F,连接DF.∠BEC=∠ADF,试证明四边形ABCD是菱形.
25.如图,在 ABCD中,G为BC边上一点,DG=DC,延长DG交AB的延长线于点E,过点A作AF∥ED交CD的延长线于点F.求证:四边形AEDF是菱形.
26.在 ABCD中,对角线AC、BD交于点O,E是边BC延长线上的动点,过点E作EF⊥BD于F,且与CD、AD分别交于点G、H,连接OH.
(1)如图,若AC⊥AB,OF=OC,求证:FG=CG;
(2)若在点E运动的过程中,存在四边形OCGH是菱形的情形,试探究 ABCD的边和角需要满足的条件.
27.已知:如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别是
E,F,且BE=DF.
(1)求证:△ABE≌△ADF;
(2)求证:四边形ABCD是菱形.
28.如图,点E、F分别在 ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,求证:四边形AECF是菱形.
29.如图,已知BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,垂足分别为E、D,联结CD、DE,DE与AB交于点O,CD∥AB.求证:四边形OBCD是菱形.
30.如图,在平行四边形ABCD中,E,F是对角线BD上的点,且BE=DF,连接AE,CF.
(1)求证△ADE≌△CBF;
(2)连接AF,CE,若AB=AD,求证:四边形AFCE是菱形.
参考答案
1.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:∵四边形BNDM是菱形,
∴BM=BN=DM=DN,
设BN=DN=x,则CN=BC﹣BN=16﹣x,
在Rt△CDN中,由勾股定理得:CD2+CN2=DN2,
即82+(16﹣x)2=x2,
解得:x=10,
即BN=10,
∴菱形BNDM的周长=4BN=40.
2.证明:(1)∵BE∥AC,OE∥AB,
∴四边形ABEO是平行四边形,
∵四边形ABCD是平行四边形,
∴AC=2AO,
∵AC=2AB,
∴AO=AB,
∴四边形ABEO是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AO=AC=,OB=BD=2,
连接AE交BO于M,
由(1)知,四边形ABEO是菱形,
∴AE、OB互相垂直平分,
∴OM=BO=1,
∴AM=,
∴AE=4,
∴四边形ABEO的面积=AE OB=.
3.(1)解:∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形,
∴OA=OC=AC=8,OB=OD=BD=6,AC⊥BD,
∴∠AOB=90°,
∴AB===10;
(2)证明:∵CE∥BD,BE∥AC,
∴四边形OBEC是平行四边形,
由(1)得:四边形ABCD是菱形,
∴AD=BC,AC⊥BD,
∴∠BOC=90°,
∴平行四边形OBEC是矩形,
∴OE=BC,
∴OE=AD;
(3)解:过D作DH⊥BC于H,如图2所示:
∵四边形ABCD是菱形,
∴BC=AB=10,菱形ABCD的面积=BC×DH=AC×BD,
即10DH=×16×12,
∴DH=,
在Rt△BDH中,由勾股定理得:BH===,
由(2)得:四边形OBEC是矩形,
∴PB=PC,
∵∠BOC=90°,
∴PB=BC=5,
∴PH=BH﹣PB=﹣5=,
在Rt△PDH中,DP===.
4.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴平行四边形DBFC是菱形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
过C作CM⊥BF于M,如图所示:
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=CM=,
∴AC=2AE=2,
故答案为:2.
5.(1)证明:∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠EDB,
∴BE=DE,
∴平行四边形BEDF是菱形;
(2)解:过点D作DH⊥BC于点H,如图所示:
∵四边形BEDF是菱形,
∴BF=DF=DE,
∴∠FBD=∠FDB=∠BDE=15°,
∴∠DFH=30°,
∵DH⊥BC,
∴∠DHF=∠DHC=90°,
∴DH=DF,
∵∠C=45°,
∴△CDH是等腰直角三角形,
∴DH=CH=CD=×2=2,
∴DF=2DH=4,
∴DE=4.
6.(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
∴AF=DB,
又∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,
∴平行四边形ADCF是菱形;
(2)解:∵D是BC的中点,
∴△ACD的面积=△ABD的面积=△ABC的面积,
∵四边形ADCF是菱形,
∴菱形ADCF的面积=2△ACD的面积=△ABC的面积=AC×AB=×4×5=10.
7.证明:(1)∵△ADF≌△ABC,
∴AB=AD=AF=AC,BC=DF,∠BAC=∠DAF=30°,
∴∠BAD=∠CAF=120°,
∴∠ABD=∠ADB=30°,∠ACF=∠AFC=30°,
∴∠DAF=∠ADB=30°,∠ACF=∠BAC=30°,
∴AF∥BD,AB∥CF,
∴四边形ABEF平行四边形,
又∵AB=AF,
∴四边形ABEF是菱形;
(2)如图,过点A作AH⊥CF于H,
∵AC=AF,∠AFC=30°,AH⊥CF,
∴CH=FH,AH=AF=1,
∴FH===,
∴CF=2,
∵四边形ABEF是菱形,
∴EF=AF=2,
∴CE=2﹣2.
8.(1)证明:如图,连接BD,
∵四边形ABCD是菱形,
∴AC⊥DB,AD=AB,
∵EM⊥AC,
∴ME∥BD,
∵点E是AB的中点,
∴点M是AD的中点,AE=AB,
∴AM=AD,
∴AM=AE.
(2)解:①由(1)得,点M是AD的中点,
∴AM=MD,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠F=∠AEM,∠EAM=∠FDM,
∴△MDF≌△MAE(AAS),
∴AE=DF,
∵AB=2AE,DF=2,
∴AB=4,
∴菱形ABCD的周长为4AB=4×4=16.
②如图,连接CM,记EF与AC交点为点G,
∵AM=AE,△MAE≌△MDF,
∴DF=DM,MF=ME,
∴∠DMF=∠DFM,
∴∠ADC=2∠DFM,
∵∠ADC=2∠MCD,
∴∠MCD=∠DFM,
∴MF=MC=ME,∠EMC=2∠FDM=∠MDC,
∵ME⊥AC,AM=ME,
∴∠MGC=90°,ME=2MG,
∴MC=2MG,
∴∠GMC=60°,
∴∠ADC=60°,
∴∠MCD=30°,
∴∠DMC=90°,
∴△DMC为直角三角形,
∵DF=2,
∴DM=2,CD=4,
∴CM==2,
∴ME=2.
9.(1)证明:连接BF,如图所示:∵EF是线段AB的垂直平分线,
∴AF=BF,
∵四边形ABCD是菱形,
∴BC=DC,∠BCF=∠DCF,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴BF=DF,
∴AF=DF;
(2)解:由(1)得:△BCF≌△DCF,
∴∠FDC=∠FBC,
∵四边形ABCD是菱形,
∴AB=BC,∠BAC=∠BAD=×70°=35°,AD∥BC,
∴∠BCF=∠DCF=∠BAC,∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,
∴∠FBA=∠BAC=35°,
∴∠FBC=∠ABC﹣∠ABF=110°﹣35°=75°,
∴∠FDC=∠FBC=75°.
10.(1)证明:四边形ABCD是菱形,
∴OB=OD,AC⊥BD,
∵BF=DE,
∴BF﹣OB=DE﹣OD,
∴OF=OE,
∴AE=AF;
(2)解:∵四边形ABCD是菱形,
∴OB=OD,AC⊥BD,OA=OC,
∵BD=2AC=16,
∴OA=4,OB=8,
设BE=AE=x,则OE=OB﹣BE=8﹣x,
在Rt△AOE中,AE2=OA2+OE2,
∴x2=(8﹣x)2+42,
解得x=5,
∴OE=8﹣5=3,
由(1)知OF=OE,
∴EF=2OE=6.
11.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠DAB=∠DCB,
∴∠BAC=∠DCA,
∵BE⊥AD,DF⊥BC,
∴∠DAB+∠ABM=90°,∠DCB+∠CDN=90°,
又∵∠DAB=∠DCB,
∴∠ABM=∠CDN,
在△ABM和△CDN中,
,
∴△ABM≌△CDN(ASA);
(2)解:四边形MBND是菱形,理由如下:
∵BE⊥AD,DF⊥BC,AD∥BC,
∴BE∥DF,
由(1)知△ABM≌△CDN,
∴BM=DN,
∴四边形MBND是平行四边形,
连接BD,如图所示:
∵四边形ABCD是菱形,
∴AC⊥BD,
即MN⊥BD,
∴平行四边形MBND是菱形.
12.解:(1)连接AC,
∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是正三角形,
∴AB=AC,∠ACB=60°,
∴∠ACF=∠ACB=60°,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴∠BAE=∠CAF,
∴∠EAF=∠EAC+∠CAF=∠EAC+∠BAE=60°,
故答案为60°;
(2)由(1)可知,△ABE≌△ACF,
∴AE=AF,
(3)当∠BAE=30°时,
∵∠B=60°,
∴∠AEB=90°,
∵∴△ABC是正三角形,
∴E为BC中点,
∴F为CD中点,
在Rt△ABE中,AB=6,BE=3,
∴AE==3,
过点F作FH⊥CG于点H,
∵F为CD中点,FH∥AE,
∴FH为△AEG中位线,
∴FH==,
∴点F到BG的距离.
13.(1)证明:∵DE⊥AB,
∴∠AED=∠DEB=90°,
∵∠BAD=45°,
∴∠ADE=∠BAD=45°,
∴AE=DE,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠OAB+∠ABD=∠BDE+∠ABD=90°,
∴∠OAB=∠BDE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(ASA);
(2)解:由(1)知,△AEF≌△DEB,
∴EF=EB,
∴AB=AE+EB=DE+EF=10,
∵四边形ABCD是菱形,
∴菱形ABCD的周长=4AB=4×10=40.
14.(1)证明:∵四边形ABCD是菱形,
∴CB=CD,
∵BE⊥CD于点E,DF⊥BC于点F,
∴∠BEC=∠DFC=90°,
在△BEC与△DFC中,
,
∴△BEC≌△DFC(AAS),
∴EC=FC,
∴BF=DE;
(2)解:∵∠A=45°,四边形ABCD是菱形,
∴∠C=∠A=45°,AG∥BC,AB=BC,
∴∠CBG=∠G=45°,
∴△DEG与△BEC是等腰直角三角形,
∵BE=CE=4,
∴AB=BC=AD=4,
∵∠A=∠G=45°,
∴∠ABG=90°,
∴AG=8,
∴DG=AG﹣AD=8﹣4.
15.证明:(1)∵四边形AECF是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵点E、F为对角线BD的三等分点,
∴BE=EF=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是菱形,
∴AE=AF=CF=CE,
又∵AE=BE,
∴AE=BE=EF=AF=DF,
∴∠EAB=∠EBA,∠EAF=∠EFA,∠FAD=∠FDA,△AEF是等边三角形,
∴∠EAF=∠AFE=∠AEF=60°,
∴∠BAE=30°,∠FAD=30°,
∴∠BAD=120°.
16.(1)证明:∵四边形ABCD是菱形,
∴OA=AC,OB=OD=BD=3,AC⊥BD,
∴∠AOB=90°,
∴OA===4,
∴AC=2OA=8,
∵E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴EF=BD=4,
(2)四边形DEOF是菱形.理由如下:
∵四边形ABCD是菱形,
∴DA=DC,OA=OC,OB=OD,
∴O是AC,BD的中点,
∵E,F分别是菱形ABCD的边AD,CD的中点,
∴DE=DA,DF=DC,OE,OF分别是△ACD和△CDA的中位线,
∴DE=DF,OE∥FD,OF∥DE,
∴四边形DEOF平行四边形,
∵DE=DF,
∴四边形DEOF是菱形.
17.解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AO,BD=2DO=10,
∵AD=AE,
∴AD=AE=AO+OE=1+OA,
∵AD2=OD2+AO2,
∴(1+OA)2=25+AO2,
∴AO=12,
∴AC=24,
∴菱形ABCD的面积==120;
(2)如图,过点G作GH⊥AC于H,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,AD=CD,∠DAC=∠DCA,
∵OE=OD,
∴∠DEO=∠EDO=45°,
∵GH⊥AC,
∴∠HED=∠HGE=45°,
∴GH=HE,GE=GH,
设∠DAC=∠DCA=x,
∴∠EDC=45°﹣x=∠GDF,
∵AF⊥CF,
∴∠FGD=90°﹣∠GDF=45°+x,
∵∠DAF=90°﹣2x,
∴∠ADC=180°﹣∠GAD﹣∠AGD=45°+x,
∴∠ADC=∠AGD,
∴AG=AD,
在△AHG和△DOA中,
,
∴△AHG≌△DOA(AAS),
∴GH=AO,
∴GE=GH=AO.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
19.解:(1)∵点Q从点A出发沿AC方向以每秒1个单位长度的速度向点C匀速运动,
∴AQ=t,
∵∠C=90°,AC=20,∠A=60°,
∴∠B=30°,
∴AB=2AC=40,
∴AP=AB﹣BP=40﹣2t,
∵PM⊥BC,
∴∠PMB=90°,
∴PM=PB=t.
故答案为:t,40﹣2t,t;
(2)存在,理由如下:
由(1)知:AQ=PM,
∵AC⊥BC,PM⊥BC,
∴AQ∥PM,
∴四边形AQMP是平行四边形,
当AP=AQ时,平行四边形AQMP是菱形,
即40﹣2t=t,
解得t=,
则存在t=,使得平行四边形AQMP成为菱形.
20.(1)证明:∵AF=FG,
∴∠FAG=∠FGA,
∵AG 平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,∠CGE=∠GED,
∴∠C=90°,
∵F是AD的中点,FG∥AE,
∴FH是△ADE的中位线,
∴H是ED的中点
∴FG是线段ED的垂直平分线,
∴GE=GD,∠DHG=90°,
∴∠GDE=∠GED,
∴∠CGE=∠GDE,
在△ECG和△GHD中,
,
∴△ECG≌△GHD(AAS);
(2)解:当∠B为30°,四边形AEGF为菱形,理由如下:
由(1)得:DE∥BC,
∴∠ADE=∠B=30°,
∴AE=AD,
∴AE=AF=FG,
由(1)得:AE∥FG,
∴四边形AEGF是平行四边形,
∵AE=AF,
∴四边形AEGF是菱形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠DBC,
∵CQ∥DB,
∴∠BCQ=∠DBC,
∴∠ADB=∠BCQ
∵DP=CQ,
∴△ADP≌△BCQ(SAS),
∴AP=BQ;
(2)∵CQ∥DB,且CQ=DP,
∴四边形CQPD是平行四边形,
∴CD=PQ,CD∥PQ,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AB=PQ,AB∥PQ,
∴四边形ABQP是平行四边形,
∵△ADP≌△BCQ,
∴∠APD=∠BQC,
∵∠APD+∠APB=180°,∠ABP+∠BQC=180°,
∴∠ABP=∠APB,
∴AB=AP,
∴四边形ABQP是菱形.
22.(1)证明:在△ACD中,点O,E分别为边AC,AD中点,
∴OE为△ACD的中位线,
∴OE∥CD,,
又∵,
∴OF∥CD,OF=CD,
∴四边形OCDF为平行四边形,
∴FD∥OC,FD=OC,
∴∠GFD=∠GCO,∠GDF=∠GOC,
∴△FGD≌△HGO(ASA);
(2)解:当时,四边形FOCD是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OC=AC,
∵AB=AC,
∴AB=CD=OC,
由(1)得:四边形OCDF为平行四边形,
∴平行四边形FOCD是菱形,
23.(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF,
在△FCE和△BOE中,
,
∴△FCE≌△BOE(AAS);
(2)解:当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD,
∴四边形OCFD为菱形.
24.证明:∵AC是BD的垂直平分线,
∴AB=AD,BC=CD,
∴∠ABD=∠ADB,
∴∠BAF=∠DAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(SAS),
∴∠ABF=∠ADF,
∵∠BEC=∠ADF,
∴∠BEC=∠ABF,
∴AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,BC=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形.
25.证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠C,AD∥BC,AB∥CD,
∵AF∥ED,
∴四边形AEDF是平行四边形,
∵AD∥BC,
∴∠DGC=∠ADE,
∵DG=DC,
∴∠DGC=∠C,
∴∠BAD=∠ADE,
∴AE=DE,
∴平行四边形AEDF是菱形.
26.(1)证明:连接OG,如图1所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AC⊥AB,
∴AC⊥CD,
∴∠OCG=90°,
∵EF⊥BD,
∴∠OFG=90°,
在Rt△OFG和Rt△OCG中,
,
∴Rt△OFG≌Rt△OCG(HL),
∴FG=CG;
(2)解:如图2所示:
若四边形OCGH是菱形,
则OH=OC,OH∥CG,OC∥GH,
∵EF⊥BD,
∴AC⊥BD,
∴ ABCD是菱形,
∴CD=AD,OA=OC,
∴OA=OH,
∴∠OAH=∠OHA,
∵OH∥CG,
∴∠OHA=∠ADC,
∵CD=AD,
∴∠CAD=∠DCA,
∴∠CAD=∠ADC=∠DCA,
∴△ACD是等边三角形,
∴∠ADC=60°,
即要使四边形OCGH是菱形, ABCD的边和角需要满足的条件是:CD=AD,∠ADC=60°.
27.证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA);
(2)由(1)得:△ABE≌△ADF,
∴AB=AD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.
28.证明:(1)∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
又∵BE=DF,
∴AB+BE=DC+DF,
即AE=CF,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
∴AC、EF互相平分;
(2)∵AB∥DC,
∴∠AEO=∠CFO,
∵EF平分∠AEC,
∴∠AEO=∠CEO,
∴∠CEO=∠CFO
∴CE=CF,
由(1)可知,四边形AECF是平行四边形,
∴平行四边形AECF是菱形.
29.证明:∵BD、BE分别是∠ABC与∠ABF的平分线,
∴∠ABD+∠ABE=×180°=90°,
即∠EBD=90°,
又∵AE⊥BE,AD⊥BD,E、D是垂足,
∴∠AEB=∠ADB=90°,
∴四边形AEBD是矩形.
∴OB=OD,
∴∠OBD=∠ODB,
∵BD平分∠ABC,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∵CD∥AB,
∴四边形OBCD是平行四边形,
∵OB=OD,
∴平行四边形OBCD是菱形.
30.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
∵BE=DF,
∴BF=DE,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)连接AC,交BD于点O,
∵AB=AD,四边形ABCD是平行四边形,
∴四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∵BE=DF,
∴EO=FO,
∴四边形AECF是平行四边形,
又∵AC⊥BD,
∴四边形AECF是菱形.
