复数期末总复习课件——2021-2022学年高二上学期数学北师大版选修1_2(共26张PPT)
文档属性
| 名称 | 复数期末总复习课件——2021-2022学年高二上学期数学北师大版选修1_2(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 21:57:27 | ||
图片预览






文档简介
(共26张PPT)
复数的期末复习
高二期末复习
1、复数知识梳理
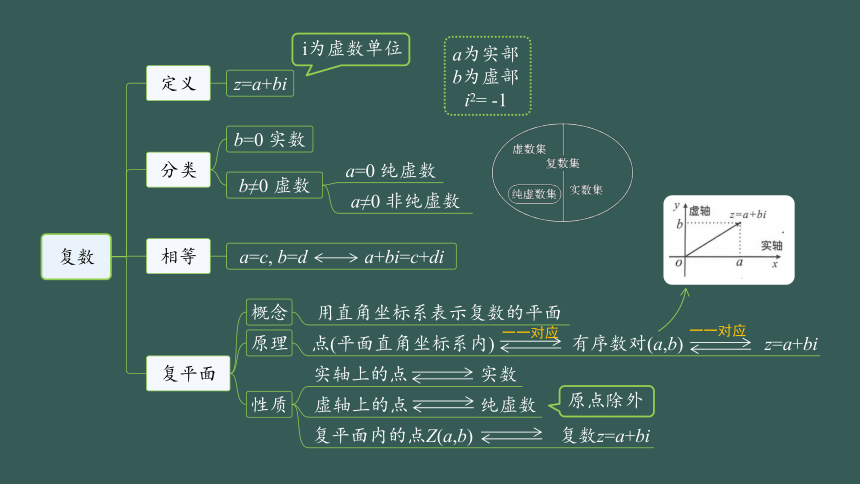
复数
定义
分类
相等
复平面
z=a+bi
b=0 实数
b≠0 虚数
a=0 纯虚数
a≠0 非纯虚数
概念
原理
性质
用直角坐标系表示复数的平面
i为虚数单位
a为实部
b为虚部i2= -1
a=c, b=d a+bi=c+di
点(平面直角坐标系内) 有序数对(a,b) z=a+bi
一一对应
一一对应
实轴上的点 实数
虚轴上的点 纯虚数
复平面内的点Z(a,b) 复数z=a+bi
原点除外
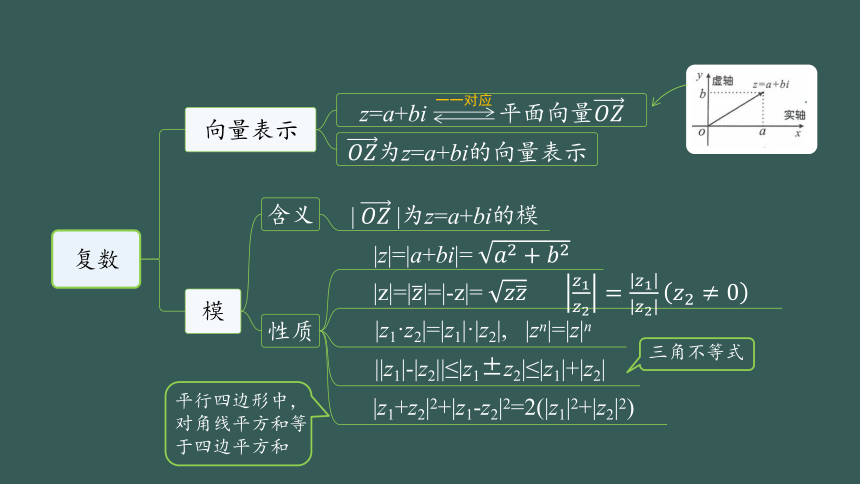
复数
向量表示
模
为z=a+bi的向量表示
含义
| |为z=a+bi的模
性质
|z|=|a+bi|=
|z|=||=|-z|=
||z1|-|z2||≤|z1±z2|≤|z1|+|z2|
|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2)
|z1·z2|=|z1|·|z2|, |zn|=|z|n
z=a+bi 平面向量
一一对应
三角不等式
平行四边形中,对角线平方和等于四边平方和
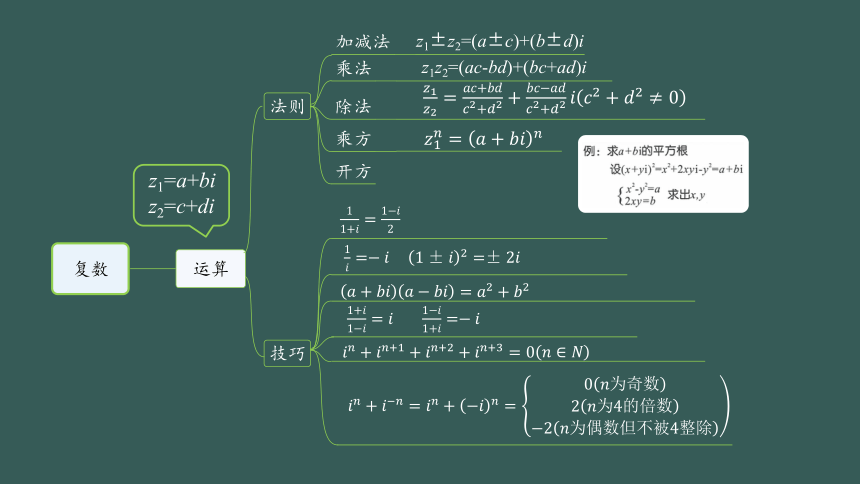
复数
运算
法则
技巧
加减法
z1±z2=(a±c)+(b±d)i
乘法
z1z2=(ac-bd)+(bc+ad)i
除法
乘方
开方
z1=a+bi
z2=c+di
复数
共轭复数
定义
表示方法
性质
实部相等,虚部互为相反数
=a-bi为z=a+bi的共轭复数
2、复数的有关概念
1.复数的共轭复数是( )
A. B. C. D.
例题剖析
A
解:
复数的共轭复数是.
2.设,则( )
A. B. C. D.
例题剖析
B
.
例题剖析
3.设,,且,
则 .
,
跟踪训练
已知,且复数是纯虚数,则_______.
所以,
复数
因为复数是纯虚数
+
解得
方法指导
(2)求一个复数的共轭复数,只需将此复数整理成标准的代数形式,实部不变,虚部变为相反数,即得原复数的共轭复数.
复数z1=a+bi与z2=c+di共轭 a=c,b=-d(a,b,c,d∈R).
解决复数概念问题的方法及注意事项
(1)求一个复数的实部与虚部,只需将已知的复数化为代数形式z=a+bi(a,b∈R),则该复数的实部为a,虚部为b.
3、复数的几何意义
1.在复平面内,复数是虚数单位,则复数z的共轭复数所对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
例题剖析
C
所对应的点为
复数z的共轭复数
位于第三象限
2.如果复数z满足,那么的最小值是( )
A. 1 B. C. 2 D.
例题剖析
A
则与的距离即为所求的最小值,.
设复数,2i,在复平面内对应的点分别为
因为,,
所以复数z的几何意义为线段,如图所示,
问题转化为:动点Z在线段上移动,求的最小值.
因此作于,
x
y
O
Z
Z2
Z0
Z1
Z3
-2
2
例题剖析
3.已知复数z满足,则的最小值为( )
A. B. C. 3 D. 2
所以的最小值为.
A
复数z满足,所以点z在以原点为圆心,1为半径的圆上,
表示复数z的对应的点与点之间的距离,
因为点与圆心的距离,
跟踪训练
在复平面内,复数z对应点,若,则( )
A. B. ,
C. D. ,
A
复数z对应点,
则,
方法指导
(1) 复数z、复平面上的点Z及向量相互联系,
即z=a+bi(a,b∈R) Z(a,b) .
1.准确理解复数的几何意义
(2) 由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.
方法指导
(1)进行简单的复数运算,将复数化为标准的代数形式;
2.解与复数的几何意义相关问题的一般步骤
(2)把复数问题转化为复平面内的点之间的关系,依据是复数a+bi(a,b∈R)与复平面上的点(a,b)一一对应.
4、复数的运算
例题剖析
1. 已知i是虚数单位,若复数z满足,则 .
2. 设i是虚数单位,若复数是纯虚数,则________.
5
例题剖析
复数是纯虚数
,且
已知a, ,复数且为虚数单位,
则 , .
,
例题剖析
,
跟踪训练
设复数,其中i是虚数单位,若为纯虚数,则实数 ; .
为纯虚数
复数运算问题
的解题策略
复数的加减法
复数的乘法
复数的除法
类比合并同类项,运用法则(实部与实部相加减,
虚部与虚部相加减)计算即可
类似于多项式相乘,然后将含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可
除法的关键是分子分母同乘以分母的共轭复数,
解题中要注意把i的幂写成最简形式
方法指导
再见
复数的期末复习
高二期末复习
1、复数知识梳理
复数
定义
分类
相等
复平面
z=a+bi
b=0 实数
b≠0 虚数
a=0 纯虚数
a≠0 非纯虚数
概念
原理
性质
用直角坐标系表示复数的平面
i为虚数单位
a为实部
b为虚部i2= -1
a=c, b=d a+bi=c+di
点(平面直角坐标系内) 有序数对(a,b) z=a+bi
一一对应
一一对应
实轴上的点 实数
虚轴上的点 纯虚数
复平面内的点Z(a,b) 复数z=a+bi
原点除外
复数
向量表示
模
为z=a+bi的向量表示
含义
| |为z=a+bi的模
性质
|z|=|a+bi|=
|z|=||=|-z|=
||z1|-|z2||≤|z1±z2|≤|z1|+|z2|
|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2)
|z1·z2|=|z1|·|z2|, |zn|=|z|n
z=a+bi 平面向量
一一对应
三角不等式
平行四边形中,对角线平方和等于四边平方和
复数
运算
法则
技巧
加减法
z1±z2=(a±c)+(b±d)i
乘法
z1z2=(ac-bd)+(bc+ad)i
除法
乘方
开方
z1=a+bi
z2=c+di
复数
共轭复数
定义
表示方法
性质
实部相等,虚部互为相反数
=a-bi为z=a+bi的共轭复数
2、复数的有关概念
1.复数的共轭复数是( )
A. B. C. D.
例题剖析
A
解:
复数的共轭复数是.
2.设,则( )
A. B. C. D.
例题剖析
B
.
例题剖析
3.设,,且,
则 .
,
跟踪训练
已知,且复数是纯虚数,则_______.
所以,
复数
因为复数是纯虚数
+
解得
方法指导
(2)求一个复数的共轭复数,只需将此复数整理成标准的代数形式,实部不变,虚部变为相反数,即得原复数的共轭复数.
复数z1=a+bi与z2=c+di共轭 a=c,b=-d(a,b,c,d∈R).
解决复数概念问题的方法及注意事项
(1)求一个复数的实部与虚部,只需将已知的复数化为代数形式z=a+bi(a,b∈R),则该复数的实部为a,虚部为b.
3、复数的几何意义
1.在复平面内,复数是虚数单位,则复数z的共轭复数所对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
例题剖析
C
所对应的点为
复数z的共轭复数
位于第三象限
2.如果复数z满足,那么的最小值是( )
A. 1 B. C. 2 D.
例题剖析
A
则与的距离即为所求的最小值,.
设复数,2i,在复平面内对应的点分别为
因为,,
所以复数z的几何意义为线段,如图所示,
问题转化为:动点Z在线段上移动,求的最小值.
因此作于,
x
y
O
Z
Z2
Z0
Z1
Z3
-2
2
例题剖析
3.已知复数z满足,则的最小值为( )
A. B. C. 3 D. 2
所以的最小值为.
A
复数z满足,所以点z在以原点为圆心,1为半径的圆上,
表示复数z的对应的点与点之间的距离,
因为点与圆心的距离,
跟踪训练
在复平面内,复数z对应点,若,则( )
A. B. ,
C. D. ,
A
复数z对应点,
则,
方法指导
(1) 复数z、复平面上的点Z及向量相互联系,
即z=a+bi(a,b∈R) Z(a,b) .
1.准确理解复数的几何意义
(2) 由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.
方法指导
(1)进行简单的复数运算,将复数化为标准的代数形式;
2.解与复数的几何意义相关问题的一般步骤
(2)把复数问题转化为复平面内的点之间的关系,依据是复数a+bi(a,b∈R)与复平面上的点(a,b)一一对应.
4、复数的运算
例题剖析
1. 已知i是虚数单位,若复数z满足,则 .
2. 设i是虚数单位,若复数是纯虚数,则________.
5
例题剖析
复数是纯虚数
,且
已知a, ,复数且为虚数单位,
则 , .
,
例题剖析
,
跟踪训练
设复数,其中i是虚数单位,若为纯虚数,则实数 ; .
为纯虚数
复数运算问题
的解题策略
复数的加减法
复数的乘法
复数的除法
类比合并同类项,运用法则(实部与实部相加减,
虚部与虚部相加减)计算即可
类似于多项式相乘,然后将含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可
除法的关键是分子分母同乘以分母的共轭复数,
解题中要注意把i的幂写成最简形式
方法指导
再见
同课章节目录
