2022年人教版八年级数学下册18.1平行四边形 同步培优 练习(Word版含答案)
文档属性
| 名称 | 2022年人教版八年级数学下册18.1平行四边形 同步培优 练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 339.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 18:54:42 | ||
图片预览


文档简介
人教版八年级数学下册:18.1平行四边形 同步培优
一、选择题
1. 如图,在 ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2, ABCD的周长是14,则DM等于( )
A. 1 B. 2 C. 3 D. 4
2. (2020·温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作□BCDE,则∠E的度数为
A.40° B.50° C.60° D.70°
3. (2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O.下列条件不能判断四边形ABCD是平行四边形的是 ( )
A. AB∥DC ,AD∥BC B. AB= DC,AD= BC
C. AB∥DC,AD =BC D.OA= OC,OB =OD
4. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A. 7 B. 9 C. 10 D. 11
5. 如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
6. (2019 广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
7. 如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么( )
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
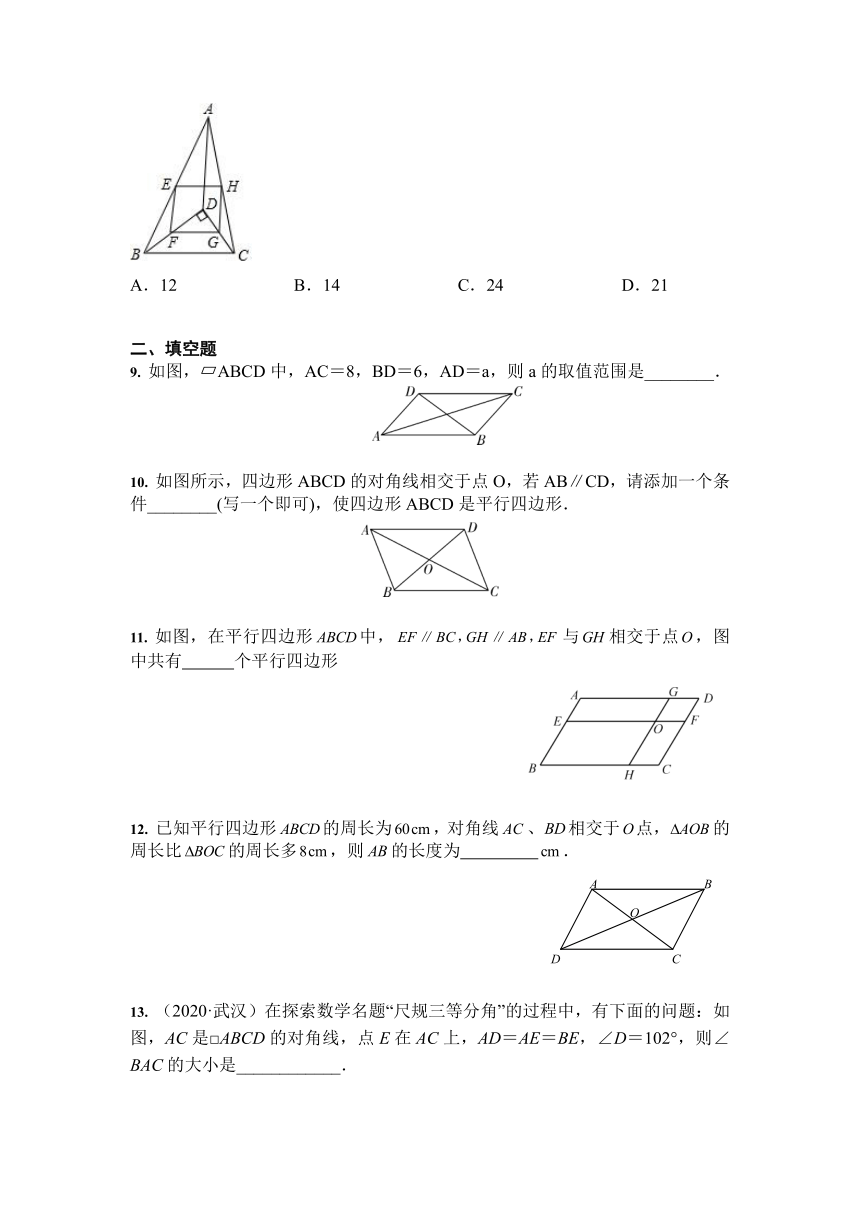
8. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为
A.12 B.14 C.24 D.21
二、填空题
9. 如图, ABCD中,AC=8,BD=6,AD=a,则a的取值范围是________.
10. 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件________(写一个即可),使四边形ABCD是平行四边形.
11. 如图,在平行四边形中,与相交于点,图中共有 个平行四边形
12. 已知平行四边形的周长为,对角线、相交于点,的周长比的周长多,则的长度为 .
13. (2020·武汉)在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是□ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是____________.
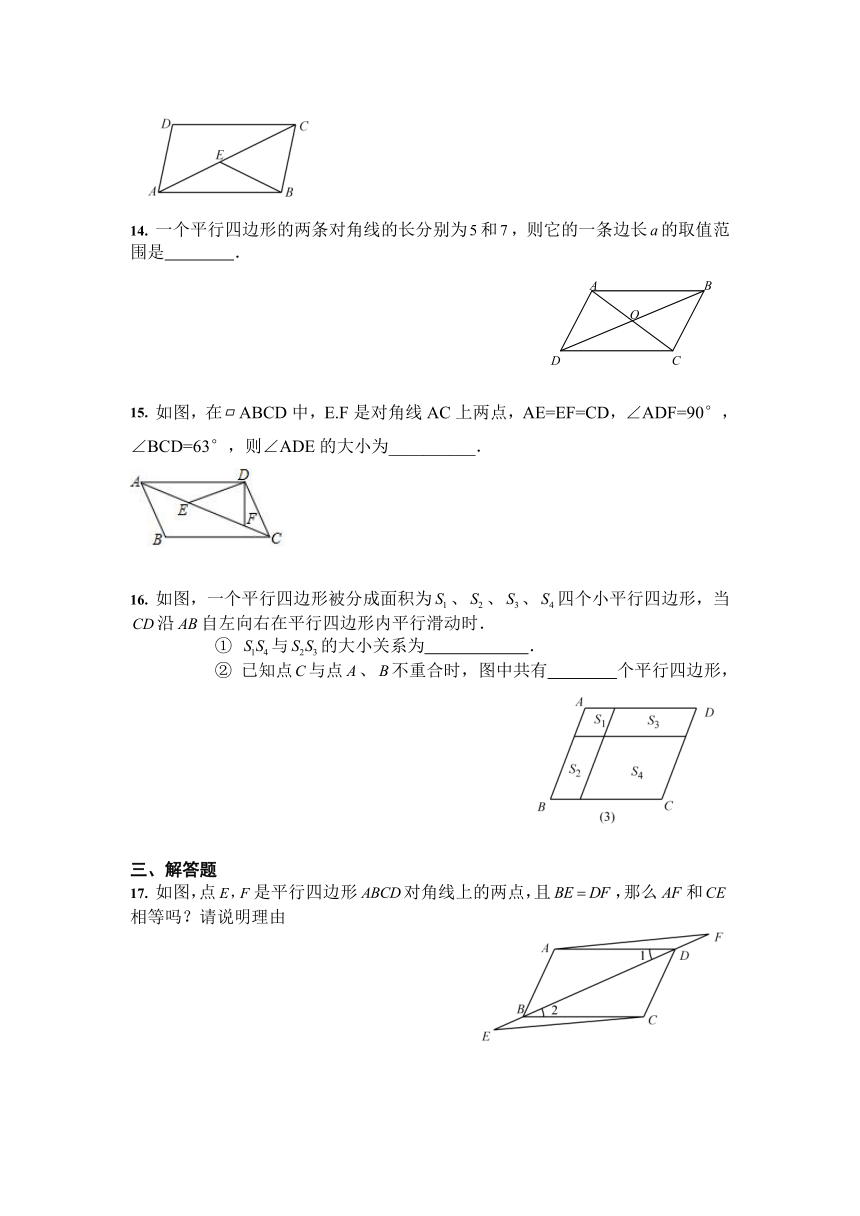
14. 一个平行四边形的两条对角线的长分别为和,则它的一条边长的取值范围是 .
15. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
16. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
三、解答题
17. 如图,点是平行四边形对角线上的两点,且,那么和相等吗?请说明理由
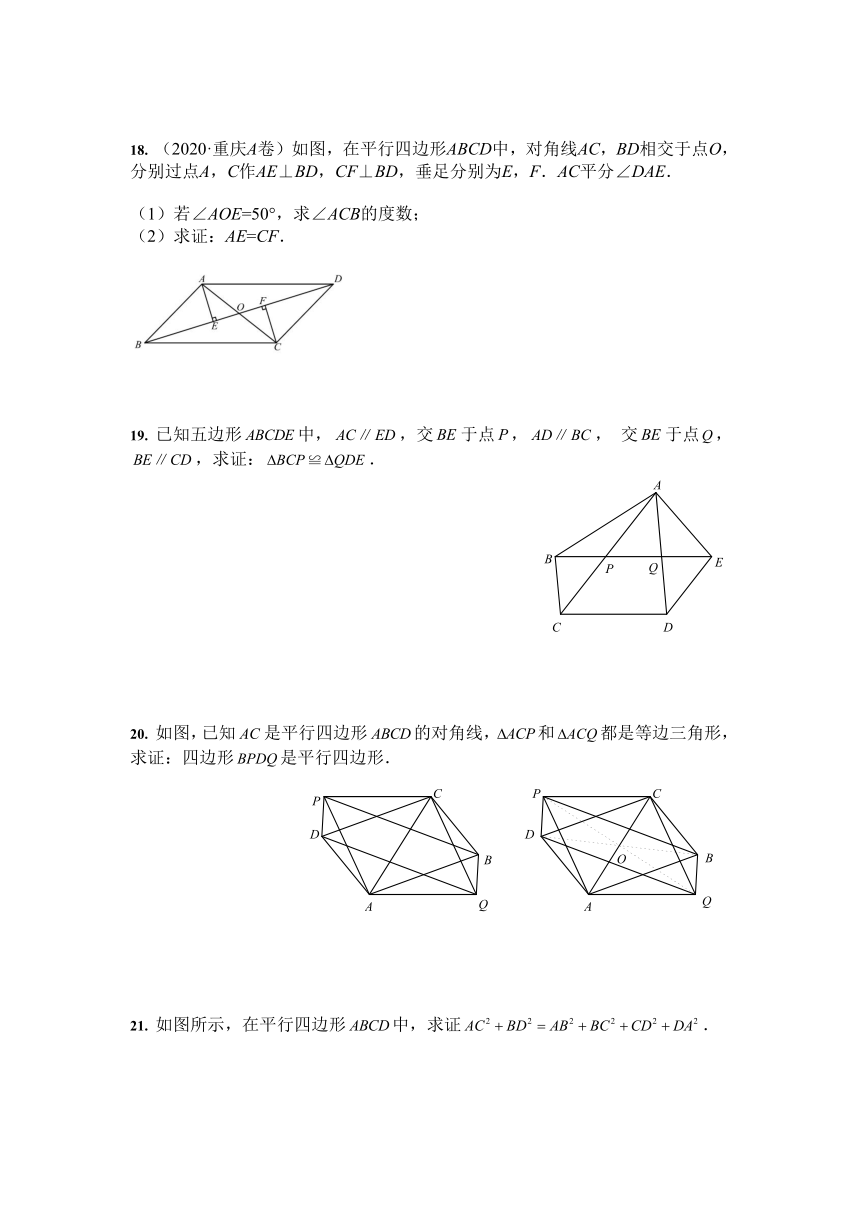
18. (2020·重庆A卷)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
19. 已知五边形中,,交于点,,交于点,,求证:.
20. 如图,已知是平行四边形的对角线,和都是等边三角形,求证:四边形是平行四边形.
21. 如图所示,在平行四边形中,求证.
人教版八年级数学下册:18.1平行四边形 同步培优-答案
一、选择题
1. 【答案】C 【解析】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABM=∠CMB,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠CBM=∠CMB,∴CB=MC=2,∴AD=BC=2,∵ ABCD的周长是14,∴AB=CD=5,∴DM=DC-MC=3.
2. 【答案】D
【解析】本题考查了等腰三角形的性质以及平行四边形的性质,由∠A=40°,AB=AC,求得∠C=70°,又因为四边形BCDE是平行四边形,所以∠E=∠C=70°,因此本题选D.
3. 【答案】C
【解析】本题考查了平行四边形的判定.注意掌握举反例的解题方法是解本题的关键.∵AB∥DC AD∥BC,∴四边形ABCD是平行四边形,故A选项能判定这个四边形是平行四边形;∵AB=DC AD=BC,∴四边形ABCD是平行四边形,故B选项能判定这个四边形是平行四边形;、∵AB∥DC AD=BC,∴四边形ABCD是平行四边形或等腰梯形,故C选项不能判定这个四边形是平行四边形.∵AO=CO BO=DO,∴四边形ABCD是平行四边形,故D选项能判定这个四边形是平行四边形;故选C.
4. 【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长 . 解题思路:
四边形EFGH的周长=EF+FG+HG+EH=11.
5. 【答案】C
6. 【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7. 【答案】C
【解析】可知四边形均为平行四边形,可知选C
8. 【答案】A
【解析】∵BD⊥CD,BD=4,CD=3,
∴BC==5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=BC,EF=GH=AD,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=7,
∴四边形EFGH的周长=7+5=12.故选A.
二、填空题
9. 【答案】1<a<7 【解析】如解图,对角线AC,BD相交于点O,则OA=AC=4,OD=BD=3,在△OAD中,OA-OD<AD<OA+OD,即1<a<7.
10. 【答案】AD∥BC(答案不唯一) 【解析】根据平行四边形的判定,在已有AB∥DC的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD∥BC”.
11. 【答案】个
12. 【答案】
【解析】如图,的周长为,的周长为
由平行四边形的对角线互相平分可得
∴.
13. 【答案】26°
【解析】本题考查了等腰三角形性质,平行四边形性质等,∵□ABCD,∴AD=BC,AD∥BC,DC∥AB,又∵AD=AE=BE,∴BC=AE=BE,∴∠BAC=∠EBA,∠BEC=∠BCE,∵AD∥BC,DC∥AB,∴∠DCB=78°,∠BAC=∠DCA,∵∠BEC=∠BAC+∠EBA,∴∠BCE=2∠BAC,∴3∠BAC=78°,解得∠BAC=26°,因此本题答案为26°.
14. 【答案】
【解析】如图,不妨设,,,在中,
,,由三角形三边关系可得
,即.
15. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
16. 【答案】①;②
三、解答题
17. 【答案】
因为是平行四边形
所以
所以,又因为,
所以
又因为,
所以,所以
18. 【答案】
解: (1)∵AE⊥BD,∴∠AEO=90°.∵∠AOE=50°,∴∠EAO=180°-90°-50°=40°.
∵AC平分∠DAE,∴∠OAD=∠EAO=40°.∵四边形ABCD为平行四边形,∴AD∥BC,∴∠ACB=∠OAD=40°.
(2)∵四边形ABCD是平行四边形,∴AO=CO.∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°.
在△AEO和△CFO中,∴△AEO≌△CFO.∴AE=CF.
19. 【答案】
∵,
∴四边形是平行四边形
∴,
∵,
∴四边形是平行四边形
∴,
∴
显然.
20. 【答案】
方法一:(利用全等得两组对边相等)
∵是平行四边形的对角线
∴
∵
∴
又∵,
∴
∴
类似可证
∴
∴四边形是平行四边形.
方法二:(利用对角线互相平分证明结论)
连结交于,连结、.
利用和是全等等边三角形可得
、、三点共线,且
又∵
∴四边形是平行四边形.
21. 【答案】
本题实质是证明.
如图所示,过点作交的延长线于点,
因为,,
故是平行四边形,从而,.
作,是垂足,则:
,
,
故.
一、选择题
1. 如图,在 ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2, ABCD的周长是14,则DM等于( )
A. 1 B. 2 C. 3 D. 4
2. (2020·温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作□BCDE,则∠E的度数为
A.40° B.50° C.60° D.70°
3. (2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O.下列条件不能判断四边形ABCD是平行四边形的是 ( )
A. AB∥DC ,AD∥BC B. AB= DC,AD= BC
C. AB∥DC,AD =BC D.OA= OC,OB =OD
4. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A. 7 B. 9 C. 10 D. 11
5. 如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
6. (2019 广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F B.∠B=∠BCF C.AC=CF D.AD=CF
7. 如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么( )
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
8. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为
A.12 B.14 C.24 D.21
二、填空题
9. 如图, ABCD中,AC=8,BD=6,AD=a,则a的取值范围是________.
10. 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件________(写一个即可),使四边形ABCD是平行四边形.
11. 如图,在平行四边形中,与相交于点,图中共有 个平行四边形
12. 已知平行四边形的周长为,对角线、相交于点,的周长比的周长多,则的长度为 .
13. (2020·武汉)在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是□ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是____________.
14. 一个平行四边形的两条对角线的长分别为和,则它的一条边长的取值范围是 .
15. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
16. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
三、解答题
17. 如图,点是平行四边形对角线上的两点,且,那么和相等吗?请说明理由
18. (2020·重庆A卷)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
19. 已知五边形中,,交于点,,交于点,,求证:.
20. 如图,已知是平行四边形的对角线,和都是等边三角形,求证:四边形是平行四边形.
21. 如图所示,在平行四边形中,求证.
人教版八年级数学下册:18.1平行四边形 同步培优-答案
一、选择题
1. 【答案】C 【解析】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABM=∠CMB,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠CBM=∠CMB,∴CB=MC=2,∴AD=BC=2,∵ ABCD的周长是14,∴AB=CD=5,∴DM=DC-MC=3.
2. 【答案】D
【解析】本题考查了等腰三角形的性质以及平行四边形的性质,由∠A=40°,AB=AC,求得∠C=70°,又因为四边形BCDE是平行四边形,所以∠E=∠C=70°,因此本题选D.
3. 【答案】C
【解析】本题考查了平行四边形的判定.注意掌握举反例的解题方法是解本题的关键.∵AB∥DC AD∥BC,∴四边形ABCD是平行四边形,故A选项能判定这个四边形是平行四边形;∵AB=DC AD=BC,∴四边形ABCD是平行四边形,故B选项能判定这个四边形是平行四边形;、∵AB∥DC AD=BC,∴四边形ABCD是平行四边形或等腰梯形,故C选项不能判定这个四边形是平行四边形.∵AO=CO BO=DO,∴四边形ABCD是平行四边形,故D选项能判定这个四边形是平行四边形;故选C.
4. 【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长 . 解题思路:
四边形EFGH的周长=EF+FG+HG+EH=11.
5. 【答案】C
6. 【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
7. 【答案】C
【解析】可知四边形均为平行四边形,可知选C
8. 【答案】A
【解析】∵BD⊥CD,BD=4,CD=3,
∴BC==5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=BC,EF=GH=AD,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=7,
∴四边形EFGH的周长=7+5=12.故选A.
二、填空题
9. 【答案】1<a<7 【解析】如解图,对角线AC,BD相交于点O,则OA=AC=4,OD=BD=3,在△OAD中,OA-OD<AD<OA+OD,即1<a<7.
10. 【答案】AD∥BC(答案不唯一) 【解析】根据平行四边形的判定,在已有AB∥DC的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD∥BC”.
11. 【答案】个
12. 【答案】
【解析】如图,的周长为,的周长为
由平行四边形的对角线互相平分可得
∴.
13. 【答案】26°
【解析】本题考查了等腰三角形性质,平行四边形性质等,∵□ABCD,∴AD=BC,AD∥BC,DC∥AB,又∵AD=AE=BE,∴BC=AE=BE,∴∠BAC=∠EBA,∠BEC=∠BCE,∵AD∥BC,DC∥AB,∴∠DCB=78°,∠BAC=∠DCA,∵∠BEC=∠BAC+∠EBA,∴∠BCE=2∠BAC,∴3∠BAC=78°,解得∠BAC=26°,因此本题答案为26°.
14. 【答案】
【解析】如图,不妨设,,,在中,
,,由三角形三边关系可得
,即.
15. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
16. 【答案】①;②
三、解答题
17. 【答案】
因为是平行四边形
所以
所以,又因为,
所以
又因为,
所以,所以
18. 【答案】
解: (1)∵AE⊥BD,∴∠AEO=90°.∵∠AOE=50°,∴∠EAO=180°-90°-50°=40°.
∵AC平分∠DAE,∴∠OAD=∠EAO=40°.∵四边形ABCD为平行四边形,∴AD∥BC,∴∠ACB=∠OAD=40°.
(2)∵四边形ABCD是平行四边形,∴AO=CO.∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°.
在△AEO和△CFO中,∴△AEO≌△CFO.∴AE=CF.
19. 【答案】
∵,
∴四边形是平行四边形
∴,
∵,
∴四边形是平行四边形
∴,
∴
显然.
20. 【答案】
方法一:(利用全等得两组对边相等)
∵是平行四边形的对角线
∴
∵
∴
又∵,
∴
∴
类似可证
∴
∴四边形是平行四边形.
方法二:(利用对角线互相平分证明结论)
连结交于,连结、.
利用和是全等等边三角形可得
、、三点共线,且
又∵
∴四边形是平行四边形.
21. 【答案】
本题实质是证明.
如图所示,过点作交的延长线于点,
因为,,
故是平行四边形,从而,.
作,是垂足,则:
,
,
故.
