2021-2022学年北师大版九年级数学下册3.2圆的对称性自主提升训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性自主提升训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-05 22:55:33 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》自主提升训练(附答案)
1.下列四个命题:
①同圆或等圆中,相等的弦所对的弧相等;
②同圆或等圆中,相等的弧所对的弦相等;
③同圆或等圆中,相等的弦的弦心距相等;
④同圆或等圆中,相等的弧所对的圆心角相等.
真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
2.以下命题:
①直径是弦; ②长度相等的弧是等弧; ③相等的弦所对的弧也相等; ④圆的对称轴是直径;
其中正确的个数是( )
A.4 B.3 C.2 D.1
3.有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
5.如图,在⊙O中,AC为⊙O直径,B为圆上一点,若∠OBC=26°,则∠AOB的度数为 .
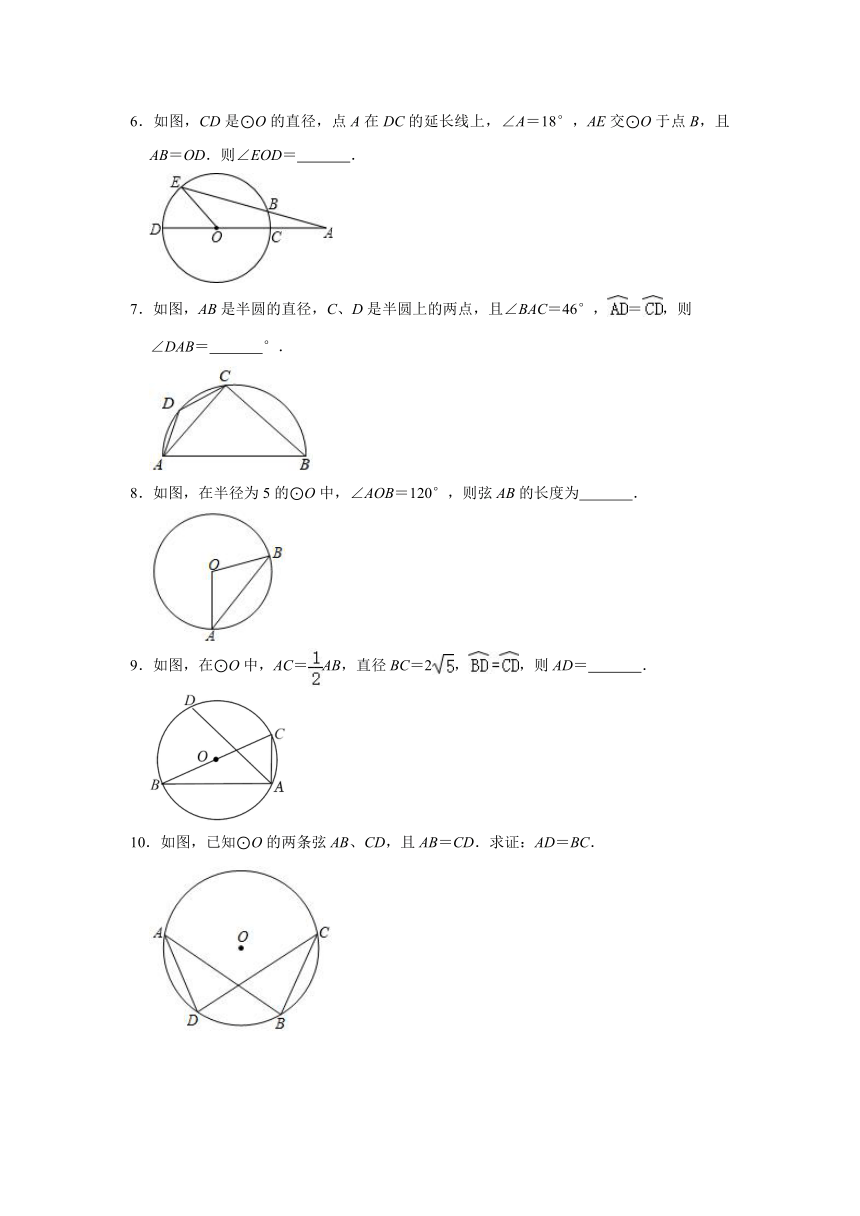
6.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°,AE交⊙O于点B,且AB=OD.则∠EOD= .
7.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
8.如图,在半径为5的⊙O中,∠AOB=120°,则弦AB的长度为 .
9.如图,在⊙O中,AC=AB,直径BC=2,,则AD= .
10.如图,已知⊙O的两条弦AB、CD,且AB=CD.求证:AD=BC.
11.如图,⊙O中的弦AB=CD,AB与CD相交于点E.求证:
(1)AC=BD;
(2)CE=BE.
12.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
13.如图,A、B是⊙O上两点,点C是弧AB的中点,∠AOB=120°.
(1)求证:四边形OACB是菱形;
(2)延长OA至P使得OA=AP,连接PC,PC=,求⊙O的半径.
14.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
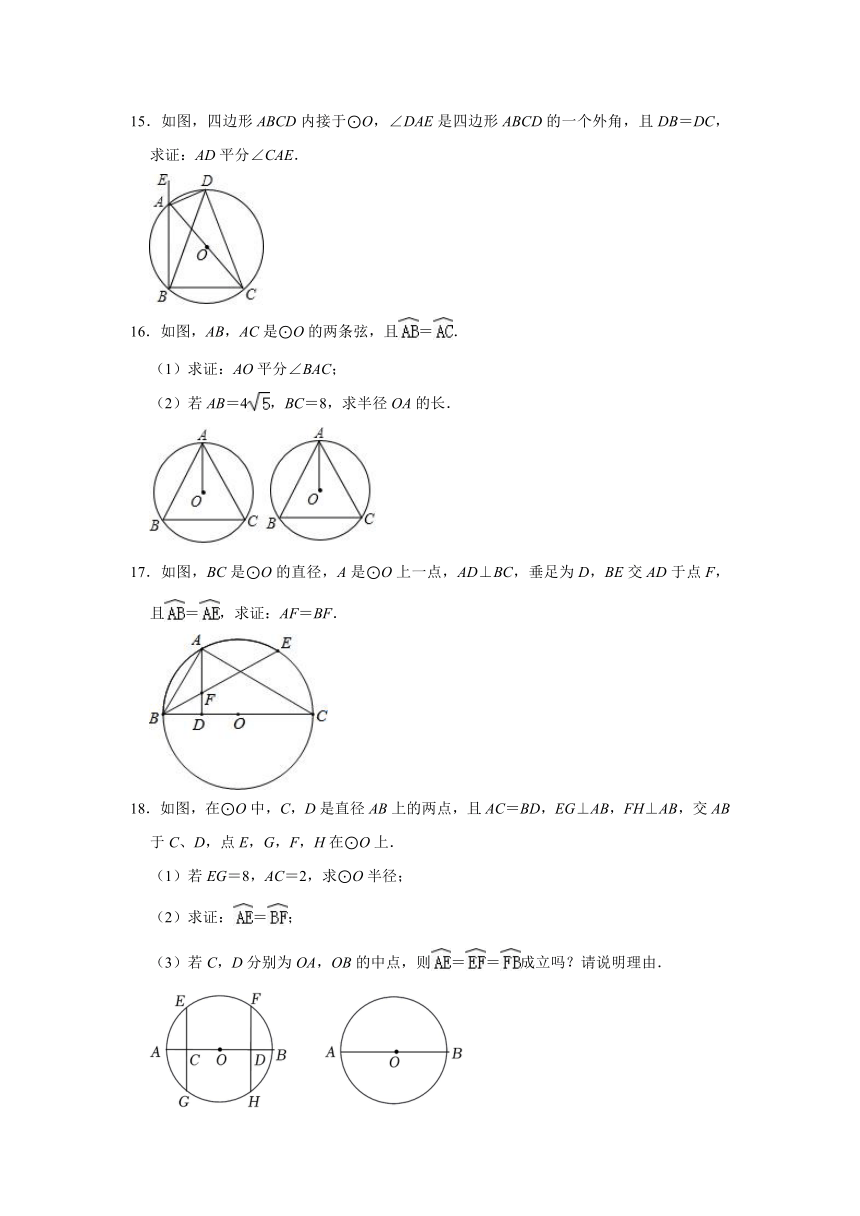
15.如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且DB=DC,求证:AD平分∠CAE.
16.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
17.如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,BE交AD于点F,且=,求证:AF=BF.
18.如图,在⊙O中,C,D是直径AB上的两点,且AC=BD,EG⊥AB,FH⊥AB,交AB于C、D,点E,G,F,H在⊙O上.
(1)若EG=8,AC=2,求⊙O半径;
(2)求证:=;
(3)若C,D分别为OA,OB的中点,则==成立吗?请说明理由.
参考答案
1.解:①同圆或等圆中,相等的弦所对的弧相等,错误,是假命题,不符合题意;
②同圆或等圆中,相等的弧所对的弦相等,正确,是真命题,符合题意;
③同圆或等圆中,相等的弦的弦心距相等,正确,是真命题,符合题意;
④同圆或等圆中,相等的弧所对的圆心角相等,正确,是真命题,符合题意,
真命题有3个,
故选:C.
2.解:①直径是弦,是真命题;
②在同圆或等圆中,长度相等的弧是等弧,原命题是假命题;
③在同圆或等圆中,相等的弦所对的弧也相等,原命题是假命题;
④圆的对称轴是直径所在的直线,原命题是假命题;
故选:D.
3.解:①正确;
②能够重合的弧叫做等弧,等弧所对的弦相等;故②正确;
③圆中90°圆周角所对的弦是直径;故③错误;
④在同圆或等圆中,相等的圆心角所对的弧相等;故④错误;
因此正确的结论是①②;
故选:B.
4.解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,
∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,
故选:A.
5.解:∵∠OBC=26°,OB=OC,
∴∠C=∠OBC=26°,
∴∠AOB=2∠C=52°,
故答案为:52°.
6.解:连接OB,
∵AB=OD,OD=OB,
∴AB=OB,
∴∠BOA=∠A,
∵∠A=18°,
∴∠BOA=18°,
∴∠EBO=∠A+∠BOA=36°,
∵OE=OB,
∴∠E=∠EBO=36°,
∵∠A=18°,
∴∠EOD=∠A+∠E=18°+36°=54°,
故答案为:54°.
7.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
8.解:作OC⊥AB于C,
则AC=BC=AB,
∵OA=OB,∠AOB=120°,
∴∠A=30°,
∴OC=OA=,
由勾股定理得,AC==,
∴AB=2AC=5,
故答案为:5.
9.解:如图,连接DB,DC,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵BC是直径,
∴∠BAC=90°,
∵BC=2,AB=2AC,
∴AC=2,AB=4,
∵∠DEA=∠EAF=∠DFA=90°,
∴四边形DEAF是矩形,
∵AD平分∠BAC,
∴DE=DF,
∴四边形DEAF是正方形,
∴AD=AF,
∵∠DAB=∠DAC,
∴=,
∴BD=CD,
∵∠DEB=∠F=90°,DB=DC,DE=DF,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF,
∴AB+AC=AE+BE=AF﹣CF=2AF=6,
∴AF=3,
∴AD=AF=3,
故答案为:3.
10.证明:∵AB=CD,
∴=,
∴﹣=﹣,
∴=,
∴AD=BC.
11.证明:(1)∵AB=CD,
∴=,
即+=+,
∴=,
∴AC=BD;
(2)∵=,
∴∠ADC=∠DAB,
∴EA=ED,
∵AB=CD,
即AE+BE=CE+DE,
∴CE=BE.
12.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
13.证明:(1)连接OC,如图,
∵C是的中点,∠AOB=l20°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
(2)∵由(1)知,△OAC是等边三角形,
∴AC=OA,∠OAC=∠ACO=60°,
∴∠PAC=120°.
又∵OA=AP,
∴AP=AC,
∴∠APC=∠ACP=30°,
∴∠PCO=∠PCA+∠ACO=90°,
即PC⊥OC.
又∵OC是半径,
∴PC是⊙O的切线,
∵PC=,
∴OC=1,
即⊙O的半径是1.
14.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
15.证明:∵DB=DC,
∴∠DBC=∠DCB,
∵∠EAD+∠BAD=180°,∠BAD+∠DCB=180°,
∴∠EAD=∠DCB,
∵∠DAC=∠DBC,
∴∠EAD=∠DAC,
∴AD平分∠CAE.
16.证明:(1)连接OB、OC,
∵=.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
17.证明:延长AD交⊙O于M,
∵BC⊥AD,BC过圆心O,
∴=,
∵=,
∴=,
∴∠BAF=∠ABF,
∴AF=BF.
18.解:(1)连接EO,
设⊙O半径为r,
∵EG⊥AB,
∴CE=CG=EG=4,
∵AC=2,
∴OC=r﹣2,
在Rt△CEO中,OE2=CE2+OC2,
∴r2=42+(r﹣2)2,
解得r=5,
∴⊙O半径为5;
(2)连接OE、OF,
∵AC=BD,OA=OB,
∴OC=OD,
∵EG⊥AB,FH⊥AB,
∴在Rt△COE和Rt△DOF中,
,
∴Rt△COE≌Rt△DOF(HL),
∴∠AOE=∠BOF,
∴=;
(3)==成立,理由如下:
∵C,D分别为OA,OB的中点,
∴OC=,
∴cos∠AOE==,
∴∠AOE=60°,
同理∠BOF=60°,
∴∠EOF=60°,
∴==.
1.下列四个命题:
①同圆或等圆中,相等的弦所对的弧相等;
②同圆或等圆中,相等的弧所对的弦相等;
③同圆或等圆中,相等的弦的弦心距相等;
④同圆或等圆中,相等的弧所对的圆心角相等.
真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
2.以下命题:
①直径是弦; ②长度相等的弧是等弧; ③相等的弦所对的弧也相等; ④圆的对称轴是直径;
其中正确的个数是( )
A.4 B.3 C.2 D.1
3.有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A.30° B.40° C.50° D.60°
5.如图,在⊙O中,AC为⊙O直径,B为圆上一点,若∠OBC=26°,则∠AOB的度数为 .
6.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°,AE交⊙O于点B,且AB=OD.则∠EOD= .
7.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
8.如图,在半径为5的⊙O中,∠AOB=120°,则弦AB的长度为 .
9.如图,在⊙O中,AC=AB,直径BC=2,,则AD= .
10.如图,已知⊙O的两条弦AB、CD,且AB=CD.求证:AD=BC.
11.如图,⊙O中的弦AB=CD,AB与CD相交于点E.求证:
(1)AC=BD;
(2)CE=BE.
12.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
13.如图,A、B是⊙O上两点,点C是弧AB的中点,∠AOB=120°.
(1)求证:四边形OACB是菱形;
(2)延长OA至P使得OA=AP,连接PC,PC=,求⊙O的半径.
14.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.
(1)求证:DF=DE;
(2)若BD=6,CE=8,求⊙O的半径.
15.如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且DB=DC,求证:AD平分∠CAE.
16.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
17.如图,BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,BE交AD于点F,且=,求证:AF=BF.
18.如图,在⊙O中,C,D是直径AB上的两点,且AC=BD,EG⊥AB,FH⊥AB,交AB于C、D,点E,G,F,H在⊙O上.
(1)若EG=8,AC=2,求⊙O半径;
(2)求证:=;
(3)若C,D分别为OA,OB的中点,则==成立吗?请说明理由.
参考答案
1.解:①同圆或等圆中,相等的弦所对的弧相等,错误,是假命题,不符合题意;
②同圆或等圆中,相等的弧所对的弦相等,正确,是真命题,符合题意;
③同圆或等圆中,相等的弦的弦心距相等,正确,是真命题,符合题意;
④同圆或等圆中,相等的弧所对的圆心角相等,正确,是真命题,符合题意,
真命题有3个,
故选:C.
2.解:①直径是弦,是真命题;
②在同圆或等圆中,长度相等的弧是等弧,原命题是假命题;
③在同圆或等圆中,相等的弦所对的弧也相等,原命题是假命题;
④圆的对称轴是直径所在的直线,原命题是假命题;
故选:D.
3.解:①正确;
②能够重合的弧叫做等弧,等弧所对的弦相等;故②正确;
③圆中90°圆周角所对的弦是直径;故③错误;
④在同圆或等圆中,相等的圆心角所对的弧相等;故④错误;
因此正确的结论是①②;
故选:B.
4.解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,
∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,
故选:A.
5.解:∵∠OBC=26°,OB=OC,
∴∠C=∠OBC=26°,
∴∠AOB=2∠C=52°,
故答案为:52°.
6.解:连接OB,
∵AB=OD,OD=OB,
∴AB=OB,
∴∠BOA=∠A,
∵∠A=18°,
∴∠BOA=18°,
∴∠EBO=∠A+∠BOA=36°,
∵OE=OB,
∴∠E=∠EBO=36°,
∵∠A=18°,
∴∠EOD=∠A+∠E=18°+36°=54°,
故答案为:54°.
7.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
8.解:作OC⊥AB于C,
则AC=BC=AB,
∵OA=OB,∠AOB=120°,
∴∠A=30°,
∴OC=OA=,
由勾股定理得,AC==,
∴AB=2AC=5,
故答案为:5.
9.解:如图,连接DB,DC,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵BC是直径,
∴∠BAC=90°,
∵BC=2,AB=2AC,
∴AC=2,AB=4,
∵∠DEA=∠EAF=∠DFA=90°,
∴四边形DEAF是矩形,
∵AD平分∠BAC,
∴DE=DF,
∴四边形DEAF是正方形,
∴AD=AF,
∵∠DAB=∠DAC,
∴=,
∴BD=CD,
∵∠DEB=∠F=90°,DB=DC,DE=DF,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF,
∴AB+AC=AE+BE=AF﹣CF=2AF=6,
∴AF=3,
∴AD=AF=3,
故答案为:3.
10.证明:∵AB=CD,
∴=,
∴﹣=﹣,
∴=,
∴AD=BC.
11.证明:(1)∵AB=CD,
∴=,
即+=+,
∴=,
∴AC=BD;
(2)∵=,
∴∠ADC=∠DAB,
∴EA=ED,
∵AB=CD,
即AE+BE=CE+DE,
∴CE=BE.
12.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
13.证明:(1)连接OC,如图,
∵C是的中点,∠AOB=l20°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
(2)∵由(1)知,△OAC是等边三角形,
∴AC=OA,∠OAC=∠ACO=60°,
∴∠PAC=120°.
又∵OA=AP,
∴AP=AC,
∴∠APC=∠ACP=30°,
∴∠PCO=∠PCA+∠ACO=90°,
即PC⊥OC.
又∵OC是半径,
∴PC是⊙O的切线,
∵PC=,
∴OC=1,
即⊙O的半径是1.
14.(1)证明:连接AD,
∵点D是的中点,
∴∠CAD=∠BAD,
∴CD=BD,
在△CAD和△BAD中,
,
∴△CAD≌△BAD(SAS),
∴∠ACD=∠ABD,
∴∠DCE=∠DBF,
在△CED和△BFD中,
,
∴△CED≌△BFD(ASA),
∴DF=DE;
(2)解:∵四边形ABDC是圆内接四边形,
∴∠DBF=∠ACD,
∵∠ACD=∠ABD,
∴∠ABD=∠DBF,
∴∠ABD=90°,
∴∠ECD=∠ABD=90°,
∴AD是⊙O的直径,
∵CD=BD=6,CE=8,
∴DE==10,
∴EB=10+6=16,
在Rt△ABE中,AB2+BE2=AE2,
设AB=AC=x,则x2+162=(x+8)2,
解得x=12,
∴AB=12,
在Rt△ABD中,AB2+BD2=AD2,
∴AD==6,
∴⊙O的半径为3.
15.证明:∵DB=DC,
∴∠DBC=∠DCB,
∵∠EAD+∠BAD=180°,∠BAD+∠DCB=180°,
∴∠EAD=∠DCB,
∵∠DAC=∠DBC,
∴∠EAD=∠DAC,
∴AD平分∠CAE.
16.证明:(1)连接OB、OC,
∵=.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
17.证明:延长AD交⊙O于M,
∵BC⊥AD,BC过圆心O,
∴=,
∵=,
∴=,
∴∠BAF=∠ABF,
∴AF=BF.
18.解:(1)连接EO,
设⊙O半径为r,
∵EG⊥AB,
∴CE=CG=EG=4,
∵AC=2,
∴OC=r﹣2,
在Rt△CEO中,OE2=CE2+OC2,
∴r2=42+(r﹣2)2,
解得r=5,
∴⊙O半径为5;
(2)连接OE、OF,
∵AC=BD,OA=OB,
∴OC=OD,
∵EG⊥AB,FH⊥AB,
∴在Rt△COE和Rt△DOF中,
,
∴Rt△COE≌Rt△DOF(HL),
∴∠AOE=∠BOF,
∴=;
(3)==成立,理由如下:
∵C,D分别为OA,OB的中点,
∴OC=,
∴cos∠AOE==,
∴∠AOE=60°,
同理∠BOF=60°,
∴∠EOF=60°,
∴==.
