2021-2022学年人教版数学八年级下册17.1勾股定理(第3课时)课件 (共34张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.1勾股定理(第3课时)课件 (共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 09:47:45 | ||
图片预览







文档简介
(共34张PPT)
人教版 · 数学· 八年级(下)
第17章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图与计算
1.学会在数轴上表示(n为正整数)的点。
2.利用勾股定理在数轴上画出长为 ( n为正整数)的线段。
学习目标
运用勾股定理解决实际问题的一般步骤
从实际问题中抽象出几何图形;
确定所求线段所在的直角三角形;
找准直角边和斜边,根据勾股定理建立等量关系;
求得结果.
1
2
3
4
回顾旧知
勾股定理应用的常见类型:
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路程问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、生活中的实际问题.
这是在海边常见的美丽的海螺.
这是数学世界中的海螺(第七届国际数
学教育大会的会徽).
导入新知
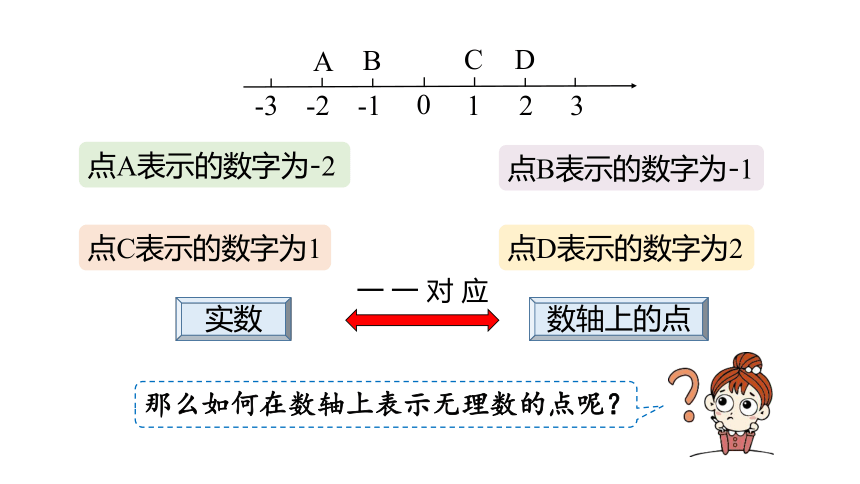
点A表示的数字为-2
点B表示的数字为-1
点C表示的数字为1
点D表示的数字为2
实数
数轴上的点
一 一 对 应
那么如何在数轴上表示无理数的点呢?
A
B
C
D
0
-1
-2
-3
1
2
3
新知 运用勾股定理作长为的线段
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示无理数的点吗?
1
1
┐
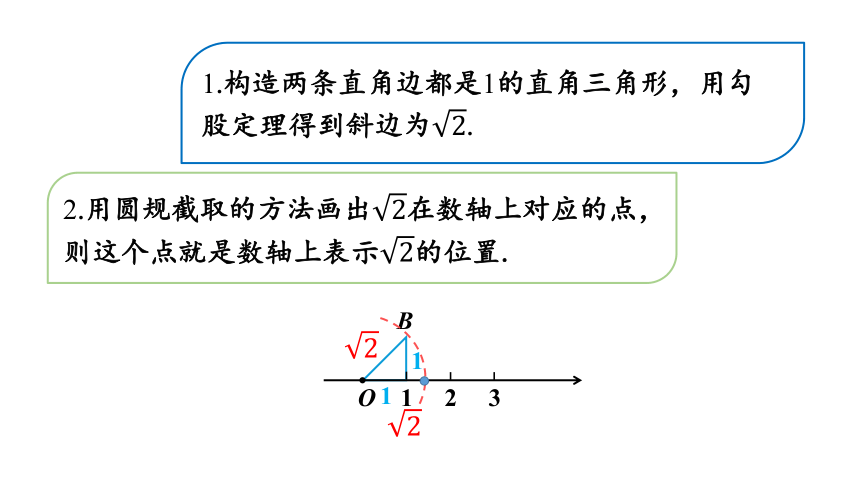
边长为1的等腰直角三角形,通过勾股定理求得斜边长为,那么在数轴上可以找到对应的点表示吗?
合作探究
1.构造两条直角边都是1的直角三角形,用勾股定理得到斜边为.
2.用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
1
1
O 1 2 3
B
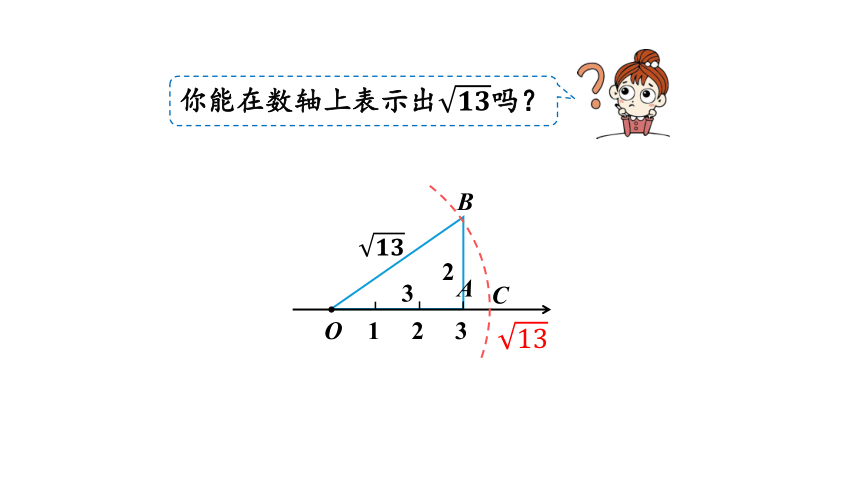
你能在数轴上表示出吗?
用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
可以看作是直角边分别为2、3的直角三角形的斜边;
在数轴上构造两条直角边为2、3的直角三角形,利用勾股定理得出斜边为;
1
2
3
2
3
O 1 2 3
A
B
C
你能在数轴上表示出吗?
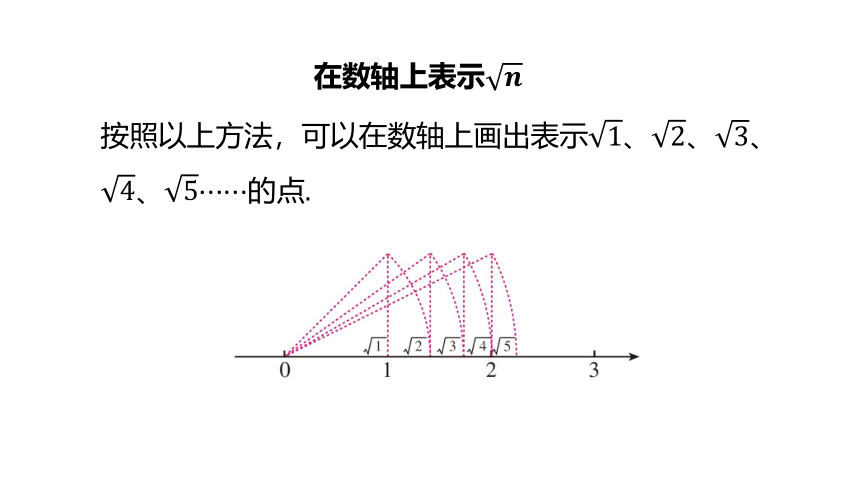
在数轴上表示
按照以上方法,可以在数轴上画出表示、、、、
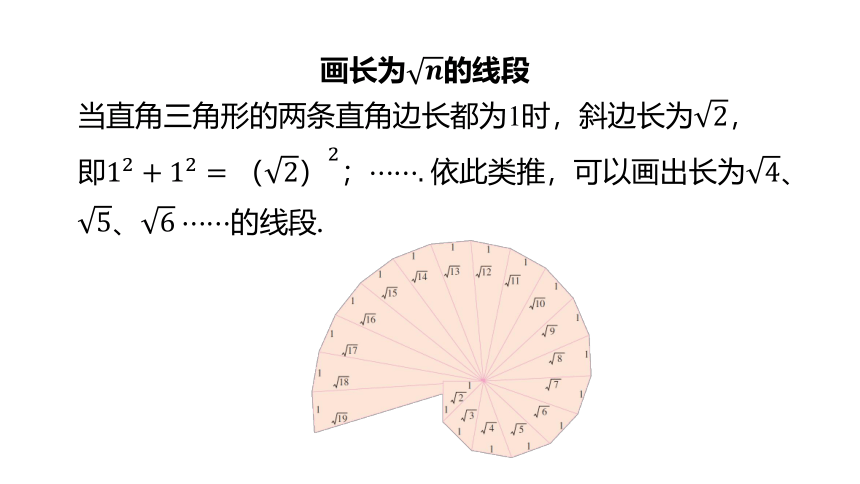
画长为的线段
当直角三角形的两条直角边长都为1时,斜边长为,
即; . 依此类推,可以画出长为、、 的线段.
(1)作一条长度等于无理数的线段的方法不唯一,应尽量利用直角边长为整数的直角三角形.
(2)并不是所有的无理数都能用尺规作图的方法在数轴上作出对应的点,如、0.1010010001等.
1.如图的正方形网格,以点 A 与网格格点为端点,你能画出几条边长为 的线段?
解: 可以看作是边长为 3 和边长为 1 的直角三角形的斜边长.
A
一共可以画出 4 条.
巩固新知
2.长为的线段是直角边长为多少的直角三角形的斜边(直角边取正整数)?
解:可以看作是直角边长为1、4的直角三角形的斜边;
可以看作是直角边长为1、5的直角三角形的斜边;
可以看作是直角边长为2、5的直角三角形的斜边.
解:如图,,
3.如图所示,在正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边有( )个.
A.0 B.1 C.2 D.3
C
A
B
C
,
.
运用勾股定理
作长为(n为大于1的整数)的线段.
(n为大于1的整数)的点.
构造边长为整数的直角三角形.
利用数轴和勾股定理.
归纳新知
D
课后练习
2.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间 B.3和4之间
C.-5和-4之间 D.4和5之间
A
3.如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为____.
知识点2:利用勾股定理解决网格图形的问题
6.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
A
D
9.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算AC2+BC2的值等于_________;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC2+BC2.
解:(2)略.
11
10.如图,方格纸上每个小正方形的边长都是1,在三个方格纸中分别画出一个三角形,使第一个三角形有一边的长为无理数,第二个三角形有两条边的长为无理数,第三个三角形的边长都是无理数.
解:答案不唯一.如:
11.如图,以数轴的两个单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是__________________.
D
13.如图,每个小正方形的边长为1,△ABC的三边长a,b,c的大小关系是( )
A.a<c<b B.a<b<c
C.c<a<b D.c<b<a
C
B
15.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为________________.
16.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,则△ABC中AB边上的高为___________.
再见
人教版 · 数学· 八年级(下)
第17章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图与计算
1.学会在数轴上表示(n为正整数)的点。
2.利用勾股定理在数轴上画出长为 ( n为正整数)的线段。
学习目标
运用勾股定理解决实际问题的一般步骤
从实际问题中抽象出几何图形;
确定所求线段所在的直角三角形;
找准直角边和斜边,根据勾股定理建立等量关系;
求得结果.
1
2
3
4
回顾旧知
勾股定理应用的常见类型:
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路程问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、生活中的实际问题.
这是在海边常见的美丽的海螺.
这是数学世界中的海螺(第七届国际数
学教育大会的会徽).
导入新知
点A表示的数字为-2
点B表示的数字为-1
点C表示的数字为1
点D表示的数字为2
实数
数轴上的点
一 一 对 应
那么如何在数轴上表示无理数的点呢?
A
B
C
D
0
-1
-2
-3
1
2
3
新知 运用勾股定理作长为的线段
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示无理数的点吗?
1
1
┐
边长为1的等腰直角三角形,通过勾股定理求得斜边长为,那么在数轴上可以找到对应的点表示吗?
合作探究
1.构造两条直角边都是1的直角三角形,用勾股定理得到斜边为.
2.用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
1
1
O 1 2 3
B
你能在数轴上表示出吗?
用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
可以看作是直角边分别为2、3的直角三角形的斜边;
在数轴上构造两条直角边为2、3的直角三角形,利用勾股定理得出斜边为;
1
2
3
2
3
O 1 2 3
A
B
C
你能在数轴上表示出吗?
在数轴上表示
按照以上方法,可以在数轴上画出表示、、、、
画长为的线段
当直角三角形的两条直角边长都为1时,斜边长为,
即; . 依此类推,可以画出长为、、 的线段.
(1)作一条长度等于无理数的线段的方法不唯一,应尽量利用直角边长为整数的直角三角形.
(2)并不是所有的无理数都能用尺规作图的方法在数轴上作出对应的点,如、0.1010010001等.
1.如图的正方形网格,以点 A 与网格格点为端点,你能画出几条边长为 的线段?
解: 可以看作是边长为 3 和边长为 1 的直角三角形的斜边长.
A
一共可以画出 4 条.
巩固新知
2.长为的线段是直角边长为多少的直角三角形的斜边(直角边取正整数)?
解:可以看作是直角边长为1、4的直角三角形的斜边;
可以看作是直角边长为1、5的直角三角形的斜边;
可以看作是直角边长为2、5的直角三角形的斜边.
解:如图,,
3.如图所示,在正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边有( )个.
A.0 B.1 C.2 D.3
C
A
B
C
,
.
运用勾股定理
作长为(n为大于1的整数)的线段.
(n为大于1的整数)的点.
构造边长为整数的直角三角形.
利用数轴和勾股定理.
归纳新知
D
课后练习
2.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间 B.3和4之间
C.-5和-4之间 D.4和5之间
A
3.如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为____.
知识点2:利用勾股定理解决网格图形的问题
6.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
A
D
9.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算AC2+BC2的值等于_________;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC2+BC2.
解:(2)略.
11
10.如图,方格纸上每个小正方形的边长都是1,在三个方格纸中分别画出一个三角形,使第一个三角形有一边的长为无理数,第二个三角形有两条边的长为无理数,第三个三角形的边长都是无理数.
解:答案不唯一.如:
11.如图,以数轴的两个单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是__________________.
D
13.如图,每个小正方形的边长为1,△ABC的三边长a,b,c的大小关系是( )
A.a<c<b B.a<b<c
C.c<a<b D.c<b<a
C
B
15.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为________________.
16.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,则△ABC中AB边上的高为___________.
再见
