2021-2022学年人教版数学八年级下册 17.1第3课时利用勾股定理作图、计算课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 17.1第3课时利用勾股定理作图、计算课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 692.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 00:00:00 | ||
图片预览


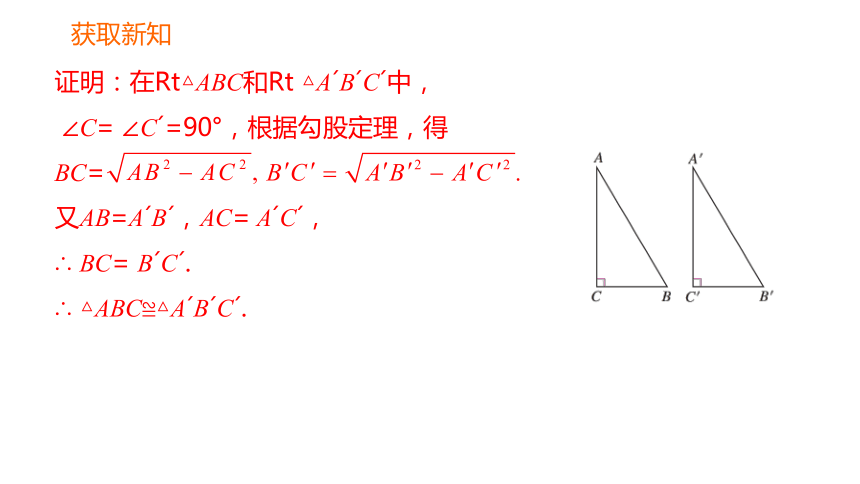
文档简介
(共18张PPT)
第十七章 勾股定理
17.1 第3课时 勾股定理作图与计算
知识回顾
回忆八年级上册学习的HL定理的内容.
斜边和一条直角边对应相等的两个直角三角形全等.
学习了勾股定理后,你可以证明这个定理吗?
证明:在Rt△ABC和Rt △A B C 中,
∠C= ∠C =90°,根据勾股定理,得
BC=
又AB=A B ,AC= A C ,
∴ BC= B C .
∴ △ABC≌△A B C .
获取新知
知识回顾
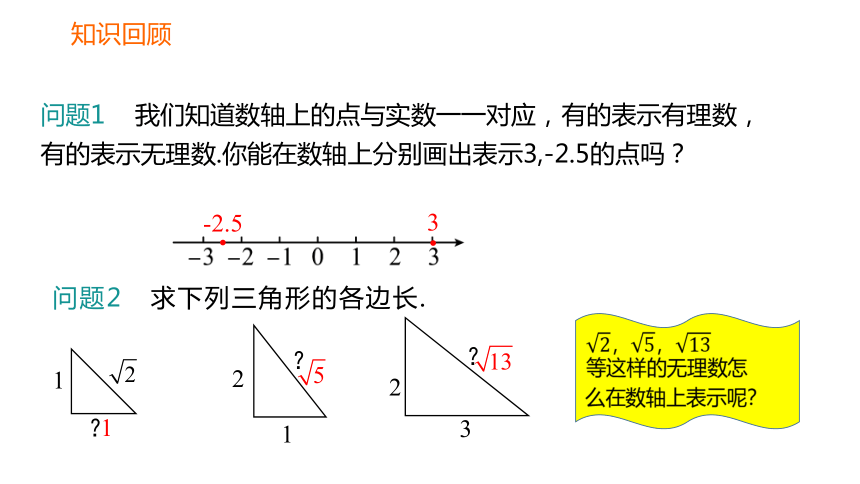
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
3
-2.5
问题2 求下列三角形的各边长.
1
2
1
2
3
?
?
?
1
获取新知
知识点一:勾股定理与数轴
-1 0 1 2 3
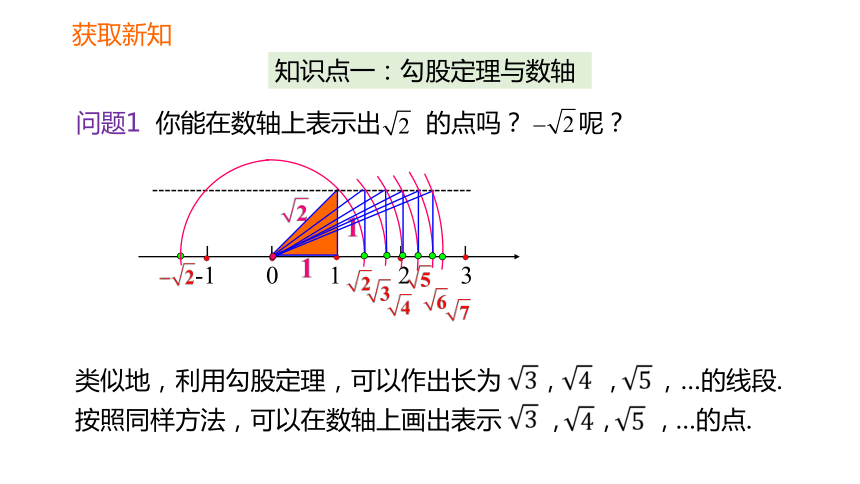
问题1 你能在数轴上表示出 的点吗? 呢?
类似地,利用勾股定理,可以作出长为 , , ,…的线段.按照同样方法,可以在数轴上画出表示 , , , …的点.
思考 根据上面问题你能在数轴上画出表示 的点吗?
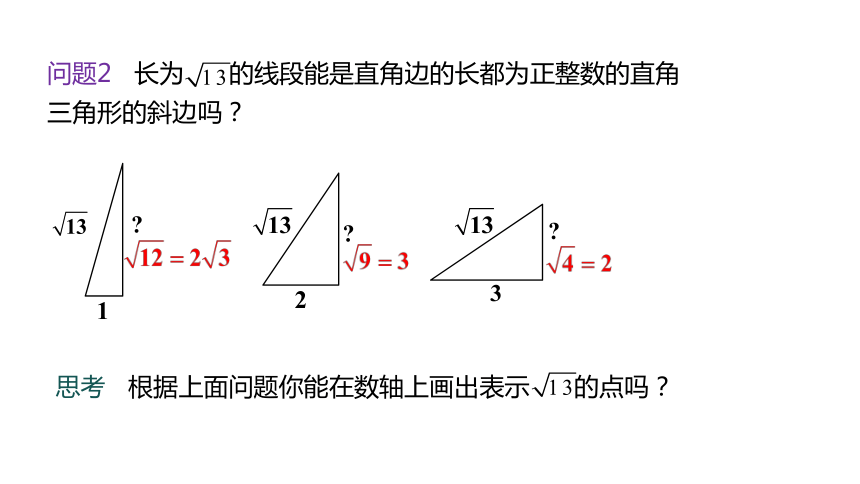
问题2 长为 的线段能是直角边的长都为正整数的直角三角形的斜边吗?
0
1
2
3
4
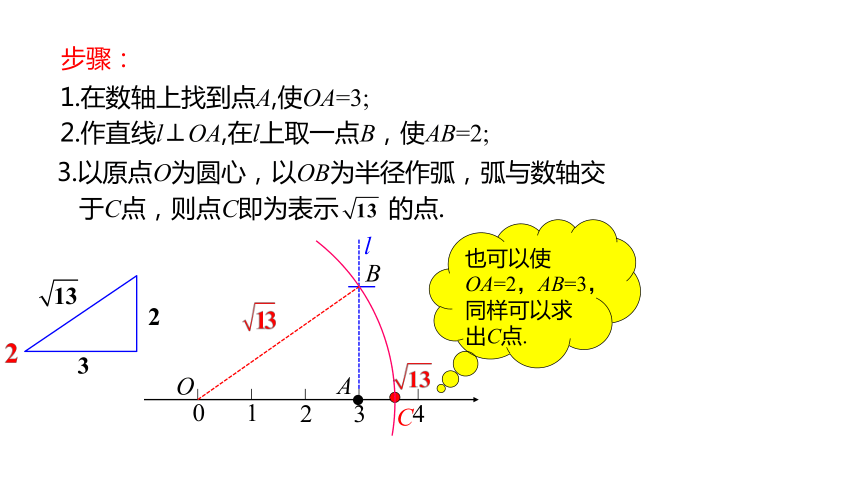
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
归纳总结
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
例题讲解
例2 你能在数轴上画出表示 的点吗?
l
A
B
C
0
1
2
3
4
解:如图所示.作法:
(1)在数轴上找出表示4(或1)的点A,则OA=4(或1);
(2)过A作直线l垂直于OA;
(3)在直线l上取点B,使AB=1(或4);
(4)以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
知识点二:勾股定理与网格
获取新知
画一画 在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为 的线段AB.
B
B
B
例3 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).
由勾股定理得
∴△ABC的周长为
例题讲解
随堂演练
1.如图,点A表示的实数是( )
D
2.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
C
3. 请在如图所示的数轴上作出 对应的点.
解:如图所示,点C即为 对应的点,
点F即为 对应的点
4.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
5. 如图,网格中每个小正方形的边长都为1,
则△ABC的周长为( )
B
课堂小结
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
通常与网格求线段长或面积结合起来
第十七章 勾股定理
17.1 第3课时 勾股定理作图与计算
知识回顾
回忆八年级上册学习的HL定理的内容.
斜边和一条直角边对应相等的两个直角三角形全等.
学习了勾股定理后,你可以证明这个定理吗?
证明:在Rt△ABC和Rt △A B C 中,
∠C= ∠C =90°,根据勾股定理,得
BC=
又AB=A B ,AC= A C ,
∴ BC= B C .
∴ △ABC≌△A B C .
获取新知
知识回顾
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-2.5的点吗?
3
-2.5
问题2 求下列三角形的各边长.
1
2
1
2
3
?
?
?
1
获取新知
知识点一:勾股定理与数轴
-1 0 1 2 3
问题1 你能在数轴上表示出 的点吗? 呢?
类似地,利用勾股定理,可以作出长为 , , ,…的线段.按照同样方法,可以在数轴上画出表示 , , , …的点.
思考 根据上面问题你能在数轴上画出表示 的点吗?
问题2 长为 的线段能是直角边的长都为正整数的直角三角形的斜边吗?
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
归纳总结
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
例题讲解
例2 你能在数轴上画出表示 的点吗?
l
A
B
C
0
1
2
3
4
解:如图所示.作法:
(1)在数轴上找出表示4(或1)的点A,则OA=4(或1);
(2)过A作直线l垂直于OA;
(3)在直线l上取点B,使AB=1(或4);
(4)以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
知识点二:勾股定理与网格
获取新知
画一画 在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为 的线段AB.
B
B
B
例3 在如图所示的6×8的网格中,每个小正方形的边长都为1,写出格点△ABC各顶点的坐标,并求出此三角形的周长.
解:由题图得A(2,2),B(-2,-1),C(3,-2).
由勾股定理得
∴△ABC的周长为
例题讲解
随堂演练
1.如图,点A表示的实数是( )
D
2.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
C
3. 请在如图所示的数轴上作出 对应的点.
解:如图所示,点C即为 对应的点,
点F即为 对应的点
4.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
5. 如图,网格中每个小正方形的边长都为1,
则△ABC的周长为( )
B
课堂小结
利用勾股定理
作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
通常与网格求线段长或面积结合起来
