2021-2022学年人教版数学八年级下册17.1勾股定理(第2课时)课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.1勾股定理(第2课时)课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 14:13:43 | ||
图片预览








文档简介
(共23张PPT)
17.1 勾股定理
人教版 · 数学· 八年级(下)
第十七章 勾股定理
第2课时 勾股定理的应用
1.能应用勾股定理计算直角三角形的边长。
2.能应用勾股定理解决简单的实际问题。
3.从实际问题中构造直角三角形解决生产、生活中的有关问题。
学习目标
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.
离开原处6尺远,花贴湖面像睡莲.
请君动脑想一想,湖水在此深几尺?
导入新知
一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
新知一 勾股定理解决线段长度问题
合作探究
【思考】
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能.
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
小于AC即可.
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
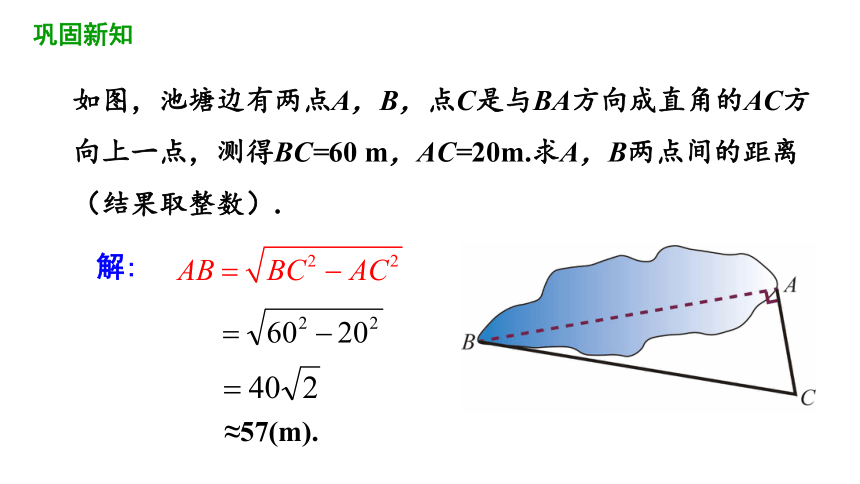
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
≈57(m).
巩固新知
如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5
米,那么梯子底端B也外移0.5米吗?
新知二 勾股定理解决线段移动问题
合作探究
C
O
D
B
A
(2)在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
解:(1)在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
OB=1.
答:梯子的底端B距墙角O为1米.
答:梯子底端B也外移约0.77米.
我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.
译:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这个水池的深度与这根芦苇的长度分别是多少?
A
B
C
巩固新知
A
B
C
解:设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52=(x+1)2 ,
解方程得x=12.
因此x+1=13
答:这个水池的深度是12尺,
这根芦苇的长度是13尺.
1.(4分)如图,是某校的长方形水泥操场,如果一学生要从A角走到C角,至少要走( C )
A.70米 B.60米 C.50米 D.45米
2.(4分)(教材P28练习T2变式)由于台风的影响,一棵树在离地面6 m处折断(如图),树顶落在离树干底部8 m处,则这棵树在折断前(不包括树根)的长度是( C )
A.8 m B.10 m C.16 m D.18 m
3.(4分)(南京中考)无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有__5__cm.
课堂练习
4.(8分)如图,要制作底边BC的长为44 cm,顶点A到BC的距离与BC长的比为1∶4的等腰三角形木衣架,则腰AB至少需要多长?(结果保留根号形式)
5.(8分)小军发现学校旗杆上端的绳子垂直到地面还多了1 m,他把绳子斜着拉直,使下端刚好触地.此时绳子下端距旗杆底部5 m,那么旗杆的高度为多少米?
解:设旗杆的高AB为x m,则绳子AC的长为(x+1)m.在△ABC中,AB2+BC2=AC2,∴x2+52=(x+1)2,解得x=12.答:旗杆的高度为12 m
6.(12分)(教材P25例2变式)如图①,一架梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C的距离为1.5米,梯子滑动后停在DE的位置上,如图②,测得梯子底端外移的长BD为0.5米,梯子顶端下滑的高度也是0.5米吗?用你所学的知识解释你的结论.
化非直角三角形为直角三角形
将实际问题转化为直角三角形模型
勾股定理的应用
归纳新知
1.“折竹抵地”问题源自《九章算术》,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈(1丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断处离地面的高度为( B )
A.5.8尺 B.4.2尺 C.3尺 D.7尺
课后练习
3.一个长、宽、高分别为4 cm、3 cm、12 cm的长方体盒子能容下的最长木棒长为__13__cm.
4.(河北中考)勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为__20__km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为__13__km.
6.如图,某地方政府决定在相距50 km的A,B两站之间的公路旁E点,修建一个土特产加工基地,且使C,D两村到E点的距离相等,已知DA⊥AB于点A,CB⊥AB于点B,DA=30 km,CB=20 km,那么基地E应建在离A站多少千米的地方?
解:设基地E应建在离A站x千米的地方,则BE=(50-x)千米,在Rt△ADE中,根据勾股定理得:DA2+AE2=302+x2=DE2,在Rt△CBE中,根据勾股定理得:CB2+BE2=202+(50-x)2=CE2,由题意可得:DE=EC,则302+x2=202+(50-x)2,解得x=20,∴基地E应建在离A站20千米的地方
7.某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6 m,8 m.现要将其扩建成等腰三角形,且扩充部分是以8 m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.
再
见
17.1 勾股定理
人教版 · 数学· 八年级(下)
第十七章 勾股定理
第2课时 勾股定理的应用
1.能应用勾股定理计算直角三角形的边长。
2.能应用勾股定理解决简单的实际问题。
3.从实际问题中构造直角三角形解决生产、生活中的有关问题。
学习目标
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.
离开原处6尺远,花贴湖面像睡莲.
请君动脑想一想,湖水在此深几尺?
导入新知
一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
新知一 勾股定理解决线段长度问题
合作探究
【思考】
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能.
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
小于AC即可.
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
≈57(m).
巩固新知
如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5
米,那么梯子底端B也外移0.5米吗?
新知二 勾股定理解决线段移动问题
合作探究
C
O
D
B
A
(2)在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
解:(1)在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
OB=1.
答:梯子的底端B距墙角O为1米.
答:梯子底端B也外移约0.77米.
我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.
译:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这个水池的深度与这根芦苇的长度分别是多少?
A
B
C
巩固新知
A
B
C
解:设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52=(x+1)2 ,
解方程得x=12.
因此x+1=13
答:这个水池的深度是12尺,
这根芦苇的长度是13尺.
1.(4分)如图,是某校的长方形水泥操场,如果一学生要从A角走到C角,至少要走( C )
A.70米 B.60米 C.50米 D.45米
2.(4分)(教材P28练习T2变式)由于台风的影响,一棵树在离地面6 m处折断(如图),树顶落在离树干底部8 m处,则这棵树在折断前(不包括树根)的长度是( C )
A.8 m B.10 m C.16 m D.18 m
3.(4分)(南京中考)无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有__5__cm.
课堂练习
4.(8分)如图,要制作底边BC的长为44 cm,顶点A到BC的距离与BC长的比为1∶4的等腰三角形木衣架,则腰AB至少需要多长?(结果保留根号形式)
5.(8分)小军发现学校旗杆上端的绳子垂直到地面还多了1 m,他把绳子斜着拉直,使下端刚好触地.此时绳子下端距旗杆底部5 m,那么旗杆的高度为多少米?
解:设旗杆的高AB为x m,则绳子AC的长为(x+1)m.在△ABC中,AB2+BC2=AC2,∴x2+52=(x+1)2,解得x=12.答:旗杆的高度为12 m
6.(12分)(教材P25例2变式)如图①,一架梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C的距离为1.5米,梯子滑动后停在DE的位置上,如图②,测得梯子底端外移的长BD为0.5米,梯子顶端下滑的高度也是0.5米吗?用你所学的知识解释你的结论.
化非直角三角形为直角三角形
将实际问题转化为直角三角形模型
勾股定理的应用
归纳新知
1.“折竹抵地”问题源自《九章算术》,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈(1丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断处离地面的高度为( B )
A.5.8尺 B.4.2尺 C.3尺 D.7尺
课后练习
3.一个长、宽、高分别为4 cm、3 cm、12 cm的长方体盒子能容下的最长木棒长为__13__cm.
4.(河北中考)勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为__20__km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为__13__km.
6.如图,某地方政府决定在相距50 km的A,B两站之间的公路旁E点,修建一个土特产加工基地,且使C,D两村到E点的距离相等,已知DA⊥AB于点A,CB⊥AB于点B,DA=30 km,CB=20 km,那么基地E应建在离A站多少千米的地方?
解:设基地E应建在离A站x千米的地方,则BE=(50-x)千米,在Rt△ADE中,根据勾股定理得:DA2+AE2=302+x2=DE2,在Rt△CBE中,根据勾股定理得:CB2+BE2=202+(50-x)2=CE2,由题意可得:DE=EC,则302+x2=202+(50-x)2,解得x=20,∴基地E应建在离A站20千米的地方
7.某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6 m,8 m.现要将其扩建成等腰三角形,且扩充部分是以8 m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.
再
见
