2021-2022年初中数学八年级下册6.2平行四边形的判定 同步课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022年初中数学八年级下册6.2平行四边形的判定 同步课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 412.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 00:26:24 | ||
图片预览




文档简介
2021-2022年初中数学八年级下册同步(北师大版)
6.2平行四边形的判定-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.能确定平行四边形的大小和形状的条件是( )
A.已知平行四边形的两邻边 B.已知平行四边形的相邻两角
C.已知平行四边形的两邻边和一条对角线 D.已知平行四边形的两条对角线
2.如图,中,,则图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
3.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( )
A.1 B.2 C.3 D.4
4.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40° B.50° C.60° D.80°
5.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
6.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是( )
A.AD=BC B.AB=CD C.AD∥BC D.∠A=∠C
二、填空题
7.已知以A,B,C,D四个点为顶点的平行四边形中,顶点A,B,C的坐标分别为,则顶点D的坐标为___________.
8.已知:如图,四边形AEFD和EBCF都是平行四边形,则四边形ABCD是__________.
9.下面是关于四边形的论断:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线和相等。以上四个条件中可以判定四边形是平行四边形的有___________(填序号).
10.已知三条线段长分别为10,14,20,以其中两条为对角线,剩余一条为边,可以画出________个平行四边形.
11.如图,ABCD的对角线BD上有两点E、F,请你添加一个条件,使四边形AECF是平行四边形,你添加的条件是___________.
12.如图所示,中,的平分线交边于点,而平分,若,则__________,__________.
三、解答题
13.如图,A,B,C是三棵树,藏宝的地点与这三棵树构成一个平行四边形,作出所有可能是藏宝地点的位置.
14.如图,由六个全等的正三角形拼成的图中,有多少个平行四边形?为什么?
15.画一个,使.
16.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.线段和的长度有什么关系?
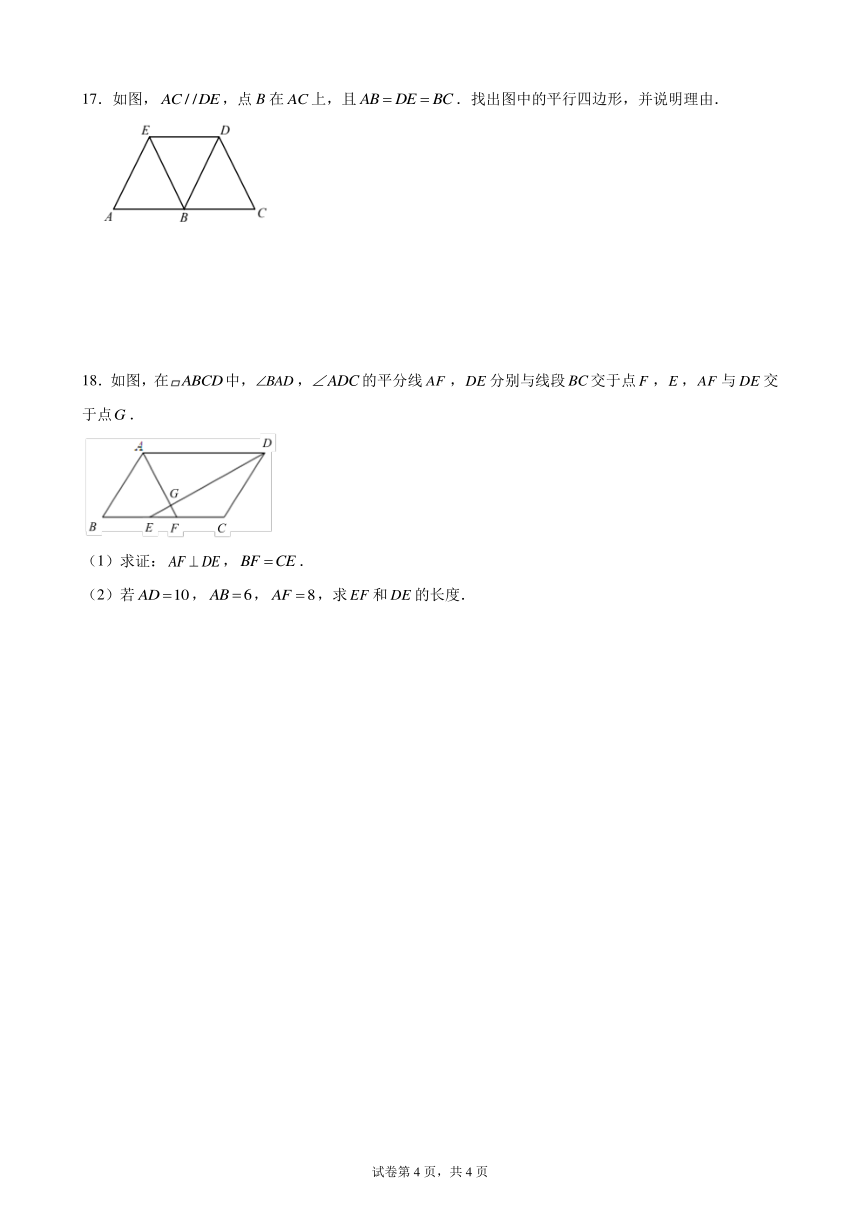
17.如图,,点B在上,且.找出图中的平行四边形,并说明理由.
18.如图,在中,,的平分线,分别与线段交于点,,与交于点.
(1)求证:,.
(2)若,,,求和的长度.
参考答案
1.C
【解析】解:A、仅仅知道平行四边形的两邻边根据平行四边形的不稳定性知不能确定其形状和大小;
B、已知平行四边形的相邻两角只能大体确定其形状,但并不能确定其大小,故错误;
C、能确定其形状及大小,故正确;
D、已知平行四边形的两对角线只能确定大小,不能确定形状,故错误.
故选:C.
2.C
【解析】根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
则图中的四边形AEOG、ABHG、AEFD、ABCD、
GOFD、GHCD、EBHO、EBCF和OHCF都是平行四边形,
共9个,
故选:C.
3.C
【解析】∵△ACE≌△BDF,
∴AC=BD、CE=DF、AE=BF,
∵AB=CD=EF,
∴平行四边形有 ACDB、 CEFD、 AEFB三个,
故选C.
4.B
【解析】解:∵AD∥BC,∠B=80°,
∴∠BAD=180°-∠B=100°.
∵AE平分∠BAD
∴∠DAE=∠BAD=50°.
∴∠AEB=∠DAE=50°
∵CF∥AE
∴∠1=∠AEB=50°.
故选B.
5.A
【解析】解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.
故选:A.
6.A
【解析】解:A、当AB∥CD,AD=BC时,四边形ABCD可能为等腰梯形,所以不能证明四边形ABCD为平行四边形;
B、AB∥CD,AB=DC,一组对边分别平行且相等,可证明四边形ABCD为平行四边形;
C、AB∥CD,AD∥BC,两组对边分别平行,可证明四边形ABCD为平行四边形;
D、∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD为平行四边形;
故选:A.
7.
【解析】解:由图可知,满足条件的点D坐标为
故答案为:
8.平行四边形
【解析】证明:∵四边形AEFD是平行四边形,
∴AD=EF,且AD∥EF,
同理可得BC=EF,且BC∥EF,
∴AD=BC,且AD∥BC,
∴四边形ABCD为平行四边形.
故答案为:平行四边形.
9.①②③
【解析】①符合平行四边形的定义,故①正确;
②两组对边分别相等,符合平行四边形的判定条件,故②正确;
③有一组对边平行且相等,符合平行四边形的判定条件,故③正确;
④对角线互相平分的四边形是平行四边形,故④错误.
所以正确的结论有①②③.
故答案为:①②③.
10.2
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,BO=OD=BD,
分为三种情况:
①AC=10,BD=14,AB=20时,AO=5,BO=7,
则5+7<20,不符合三角形三边关系定理;不能组成平行四边形;
②AC=10,BD=20,AB=14时,AO=5,BO=10,
则5+10>14,符合三角形三边关系定理;能组成平行四边形;
③AC=20,BD=14,AB=10时,AO=10,BO=7,
则7+10>10,符合三角形三边关系定理;能组成平行四边形;
可以画出不同形状的平行四边形的个数是2,
故答案为2.
11.BE=DF
【解析】解:可添加条件:BE=DF.
证明:连接AC,交BD于点O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB-BE=OD-DF,即OE=OF,
∵OA=OC,
∴四边形AECF是平行四边形.
故答案为:BE=DF.
12.60° 120°.
【解析】设,
∵AM平分,
∴,
在中,,,
∴,
∴,
在中, ,,
∴,
∴,
∴,
即,
又∵,
∴,
故答案为:(1);(2).
13.见解析.
【解析】如图:
∴M1,M2,M3为可能的藏宝地点.
14.6个,两组对边分别相等的四边形是平行四边形
【解析】解:如图所示,
∵六个三角形是全等的正三角形,
∴OA=EF,AF=OE,
∵两组对边分别相等,
∴四边形AOEF为平行四边形;
同理可证,四边形ABOF,四边形ABCO,四边形BCDO,四边形CDEO,四边形DEFO均为平行四边形,
∴共有6个平行四边形,根据两组对边分别相等的四边形是平行四边形.
15.见解析
【解析】如图,平行四边形ABCD即为所求,
16.
【解析】解:.理由如下:
如图,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴AB=DC.
17.四边形EABD和EBCD是平行四边形,理由见解析
【解析】解:∵,
∴,,
∵,
∴且,
且,
∴四边形ABDE是平行四边形,四边形BCDE是平行四边形.
18.(1)见解析;(2)EF=2,DE=
【解析】解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF=∠BAD.
∵DE平分∠ADC,
∴∠ADE=∠CDE=∠ADC.
∵四边形ABCD平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,
∴∠BAD+∠ADC=180°,
即2∠DAF+2∠ADE=180°,
∴∠DAF+∠ADE=90°,
∴∠AGD=180°-(∠DAF+∠ADE)=180°-90°=90°.
∴AF⊥DE;
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠AFB=∠BAF,
∴BF=AB,
∵AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CE=CD,
∵AB=CD,
∴BF=CE;
(2)∵BF=AB=6,
∴CE=BF=6.
∴CE+BF=12,
∵四边形ABCD平行四边形,
∴BC=AD=10.
∴10+EF=12,
∴EF=2,
过点D作DH∥AF交BC的延长线于点H.
∴∠EDH=∠AGD=90°.
∵AF∥DH,AD∥FH,
∴四边形AFHD为平行四边形.
∴DH=AF=8,FH=AD=10.
∴EH=EF+FH=2+10=12,
∴在Rt△DHE中:DE==,
∴EF的长度为2,DE的长度为.
试卷第4页,共4页
试卷第1页,共1页
6.2平行四边形的判定-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.能确定平行四边形的大小和形状的条件是( )
A.已知平行四边形的两邻边 B.已知平行四边形的相邻两角
C.已知平行四边形的两邻边和一条对角线 D.已知平行四边形的两条对角线
2.如图,中,,则图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
3.如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为( )
A.1 B.2 C.3 D.4
4.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40° B.50° C.60° D.80°
5.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
6.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是( )
A.AD=BC B.AB=CD C.AD∥BC D.∠A=∠C
二、填空题
7.已知以A,B,C,D四个点为顶点的平行四边形中,顶点A,B,C的坐标分别为,则顶点D的坐标为___________.
8.已知:如图,四边形AEFD和EBCF都是平行四边形,则四边形ABCD是__________.
9.下面是关于四边形的论断:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线和相等。以上四个条件中可以判定四边形是平行四边形的有___________(填序号).
10.已知三条线段长分别为10,14,20,以其中两条为对角线,剩余一条为边,可以画出________个平行四边形.
11.如图,ABCD的对角线BD上有两点E、F,请你添加一个条件,使四边形AECF是平行四边形,你添加的条件是___________.
12.如图所示,中,的平分线交边于点,而平分,若,则__________,__________.
三、解答题
13.如图,A,B,C是三棵树,藏宝的地点与这三棵树构成一个平行四边形,作出所有可能是藏宝地点的位置.
14.如图,由六个全等的正三角形拼成的图中,有多少个平行四边形?为什么?
15.画一个,使.
16.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.线段和的长度有什么关系?
17.如图,,点B在上,且.找出图中的平行四边形,并说明理由.
18.如图,在中,,的平分线,分别与线段交于点,,与交于点.
(1)求证:,.
(2)若,,,求和的长度.
参考答案
1.C
【解析】解:A、仅仅知道平行四边形的两邻边根据平行四边形的不稳定性知不能确定其形状和大小;
B、已知平行四边形的相邻两角只能大体确定其形状,但并不能确定其大小,故错误;
C、能确定其形状及大小,故正确;
D、已知平行四边形的两对角线只能确定大小,不能确定形状,故错误.
故选:C.
2.C
【解析】根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
则图中的四边形AEOG、ABHG、AEFD、ABCD、
GOFD、GHCD、EBHO、EBCF和OHCF都是平行四边形,
共9个,
故选:C.
3.C
【解析】∵△ACE≌△BDF,
∴AC=BD、CE=DF、AE=BF,
∵AB=CD=EF,
∴平行四边形有 ACDB、 CEFD、 AEFB三个,
故选C.
4.B
【解析】解:∵AD∥BC,∠B=80°,
∴∠BAD=180°-∠B=100°.
∵AE平分∠BAD
∴∠DAE=∠BAD=50°.
∴∠AEB=∠DAE=50°
∵CF∥AE
∴∠1=∠AEB=50°.
故选B.
5.A
【解析】解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.
故选:A.
6.A
【解析】解:A、当AB∥CD,AD=BC时,四边形ABCD可能为等腰梯形,所以不能证明四边形ABCD为平行四边形;
B、AB∥CD,AB=DC,一组对边分别平行且相等,可证明四边形ABCD为平行四边形;
C、AB∥CD,AD∥BC,两组对边分别平行,可证明四边形ABCD为平行四边形;
D、∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
∴四边形ABCD为平行四边形;
故选:A.
7.
【解析】解:由图可知,满足条件的点D坐标为
故答案为:
8.平行四边形
【解析】证明:∵四边形AEFD是平行四边形,
∴AD=EF,且AD∥EF,
同理可得BC=EF,且BC∥EF,
∴AD=BC,且AD∥BC,
∴四边形ABCD为平行四边形.
故答案为:平行四边形.
9.①②③
【解析】①符合平行四边形的定义,故①正确;
②两组对边分别相等,符合平行四边形的判定条件,故②正确;
③有一组对边平行且相等,符合平行四边形的判定条件,故③正确;
④对角线互相平分的四边形是平行四边形,故④错误.
所以正确的结论有①②③.
故答案为:①②③.
10.2
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,BO=OD=BD,
分为三种情况:
①AC=10,BD=14,AB=20时,AO=5,BO=7,
则5+7<20,不符合三角形三边关系定理;不能组成平行四边形;
②AC=10,BD=20,AB=14时,AO=5,BO=10,
则5+10>14,符合三角形三边关系定理;能组成平行四边形;
③AC=20,BD=14,AB=10时,AO=10,BO=7,
则7+10>10,符合三角形三边关系定理;能组成平行四边形;
可以画出不同形状的平行四边形的个数是2,
故答案为2.
11.BE=DF
【解析】解:可添加条件:BE=DF.
证明:连接AC,交BD于点O,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB-BE=OD-DF,即OE=OF,
∵OA=OC,
∴四边形AECF是平行四边形.
故答案为:BE=DF.
12.60° 120°.
【解析】设,
∵AM平分,
∴,
在中,,,
∴,
∴,
在中, ,,
∴,
∴,
∴,
即,
又∵,
∴,
故答案为:(1);(2).
13.见解析.
【解析】如图:
∴M1,M2,M3为可能的藏宝地点.
14.6个,两组对边分别相等的四边形是平行四边形
【解析】解:如图所示,
∵六个三角形是全等的正三角形,
∴OA=EF,AF=OE,
∵两组对边分别相等,
∴四边形AOEF为平行四边形;
同理可证,四边形ABOF,四边形ABCO,四边形BCDO,四边形CDEO,四边形DEFO均为平行四边形,
∴共有6个平行四边形,根据两组对边分别相等的四边形是平行四边形.
15.见解析
【解析】如图,平行四边形ABCD即为所求,
16.
【解析】解:.理由如下:
如图,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴AB=DC.
17.四边形EABD和EBCD是平行四边形,理由见解析
【解析】解:∵,
∴,,
∵,
∴且,
且,
∴四边形ABDE是平行四边形,四边形BCDE是平行四边形.
18.(1)见解析;(2)EF=2,DE=
【解析】解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF=∠BAD.
∵DE平分∠ADC,
∴∠ADE=∠CDE=∠ADC.
∵四边形ABCD平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,
∴∠BAD+∠ADC=180°,
即2∠DAF+2∠ADE=180°,
∴∠DAF+∠ADE=90°,
∴∠AGD=180°-(∠DAF+∠ADE)=180°-90°=90°.
∴AF⊥DE;
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠AFB=∠BAF,
∴BF=AB,
∵AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CE=CD,
∵AB=CD,
∴BF=CE;
(2)∵BF=AB=6,
∴CE=BF=6.
∴CE+BF=12,
∵四边形ABCD平行四边形,
∴BC=AD=10.
∴10+EF=12,
∴EF=2,
过点D作DH∥AF交BC的延长线于点H.
∴∠EDH=∠AGD=90°.
∵AF∥DH,AD∥FH,
∴四边形AFHD为平行四边形.
∴DH=AF=8,FH=AD=10.
∴EH=EF+FH=2+10=12,
∴在Rt△DHE中:DE==,
∴EF的长度为2,DE的长度为.
试卷第4页,共4页
试卷第1页,共1页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
