2021-2022年初中数学八年级下册6.1平行四边形的性质 同步课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022年初中数学八年级下册6.1平行四边形的性质 同步课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 396.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 00:35:26 | ||
图片预览




文档简介
2021-2022年初中数学八年级下册同步(北师大版)
6.1平行四边形的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.平行四边形具有的特征是( )
A.四个角都是直角 B.对角线相等
C.对角线互相平分 D.四边相等
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
A.4cm,6cm B.6cm,8cm C.8cm,12cm D.20cm,30cm
3.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3)
C.(7,3) D.(8,2)
4.已知四边形是平行四边形,则下列各图中与一定不相等的是( )
A. B. C. D.
5.设D为等腰底边BC上一点,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
A.2AB B.2AB+BC C.2BC D.AB+BC
6.若平行四边形相邻两边为,,它们与对边的距离分别为,,那么等于( )
A.5∶3 B.3∶5 C.10∶3 D.3∶10
二、填空题
7.若平行四边形的一边长为6,一条对角线为8,则另一条对角线a的取值范围是________.
8.如图,中,,则的长为_________.
9.如图,在中,是对角线上一点,,,则的度数为__________。
10.如图,在中,一条边的长是8,一条对角线的长为6,那么它的另一条对角线的长的取值范围是________.
11.□ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为_____.
12.已知平行四边形的面积为144,相邻两边上的高分别为8和9,则它的周长为_____.
三、解答题
13.已知 ABCD的对角线AC与BD相交于点O,OA,OB,AB的长分别为3,4,5,求其他各边以及两条对角线的长度.
14.如图,在中,,求和的度数.
15. ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
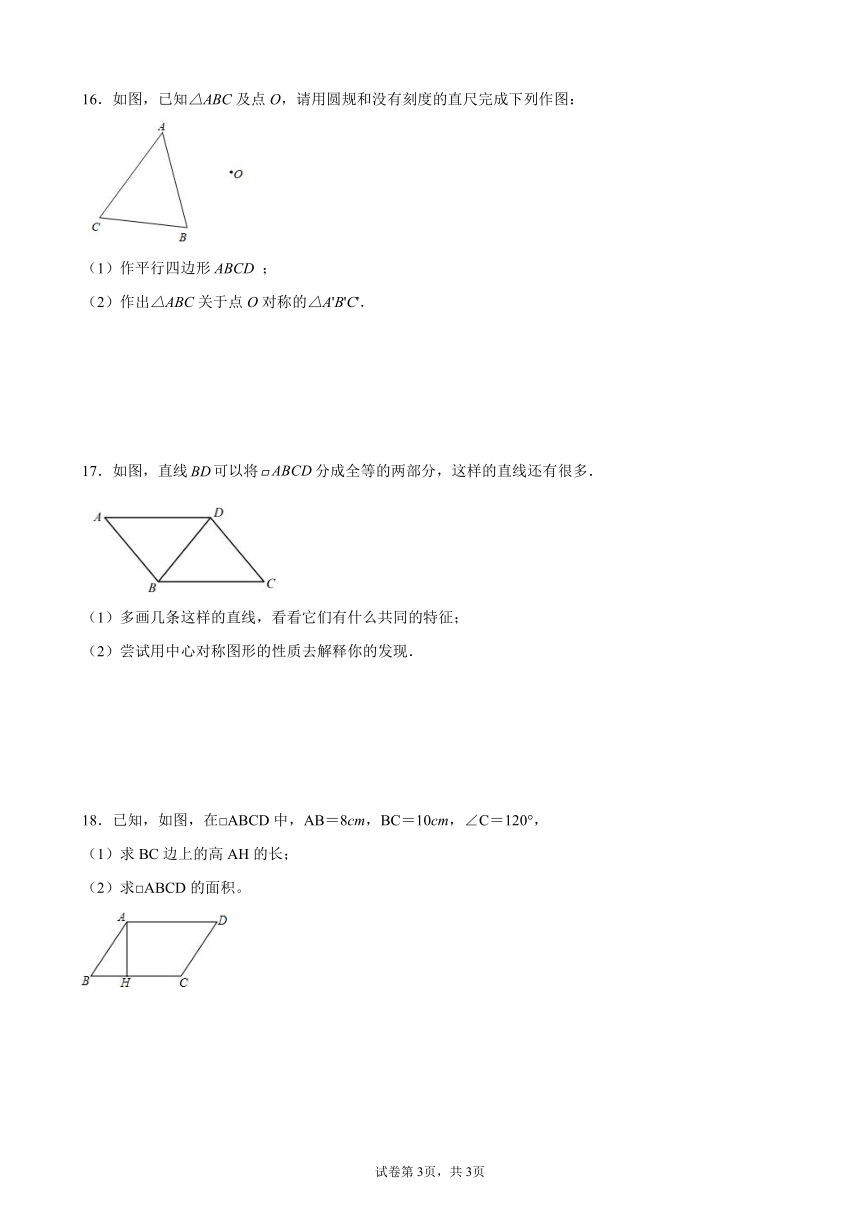
16.如图,已知△ABC及点O,请用圆规和没有刻度的直尺完成下列作图:
(1)作平行四边形ABCD ;
(2)作出△ABC关于点O对称的△A'B'C'.
17.如图,直线可以将分成全等的两部分,这样的直线还有很多.
(1)多画几条这样的直线,看看它们有什么共同的特征;
(2)尝试用中心对称图形的性质去解释你的发现.
18.已知,如图,在□ABCD中,AB=8cm,BC=10cm,∠C=120°,
(1)求BC边上的高AH的长;
(2)求□ABCD的面积。
参考答案
1.C
【解析】平行四边形对角线互相平分,对边平行且相等,对角相等.
故选C
2.D
【解析】解:由平行四边形的对角线互相平分,可得:
A、∵2+3<10, 不能构成三角形,故不符合题意;
B、 4+3<10, 不能构成三角形,故不符合题意;
C、 4+6=10, 不能构成三角形,故不符合题意;
D、 >15, 能构成三角形,故符合题意;
故选:D.
3.C
【解析】解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),
∵AB在x轴上,
∴点C与点D的纵坐标相等,都为3,
∵D点相对于A点横坐标移动了2-0=2,
∴C点横坐标为2+5=7,
∴即顶点C的坐标(7,3).
故选:C.
4.C
【解析】解:A正确;
∵∠1和∠2是对顶角,
∴∠1=∠2;
B、D正确;
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,
∴∠1=∠2;
C不正确;
∵四边形ABCD是平行四边形,
∴∠1=∠BCE,
∵∠2=∠CBE+∠BCE,
∴∠2=∠CBE+∠1,
∴∠2>∠1,即一定不相等;
故选:C.
5.A
【解析】解:∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∴DE=AF,AE=DF,
∵DF∥AC,
∴∠C=∠FDB,
∵AB=AC,
∴∠B=∠C
∴∠FDB=∠B,
∴BF=DF,
∴BF=DF=AE,
∴四边形AFDE的周长等于AE+DE+DF+AF=BF+AF+BF+AF=2AB.
故选:A
6.A
【解析】解:∵,
∴
故选:A
7.
【解析】解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC=AC=4,OB=OD=BD,
在△BOC中,BC=6,OC=4,
∴OB的取值范围是BC OC<OB<BC+OC,
即2<OB<10,
∴BD的取值范围是4<BD<20.
故答案为:.
8.
【解析】解:
故答案为:
9.21°
【解析】设.
∵,
∴,
∴.
∵.∴.
∵四边形是平行四边形,∴,
∴,
∴.
∴,解得.
即.
故答案为:21°.
10.
【解析】∵四边形是平行四边形,
∴.
在中,由三角形的三边关系,得
,
即,
∴,
∴,
即.
故答案为:.
11.
【解析】如图,过点A作AE⊥BC于点E、AF⊥CD于F,则AE=8,
由平行四边形的面积公式=底×高,可得,解得AF=.
故答案为.
12.68
【解析】由平行四边形的面积是144,相邻两边上的高分别为8和9,即可根据平行四边形的面积公式求得其相邻两边的长144÷8=18,144÷9=16,因此可得它的周长是:18+16+18+16=68.
故答案为68.
13.其他各边的长都是5,两条对角线的长分别为6,8
【解析】解:∵OA=3,OB=4,AB=5,
∴OA2+OB2=32+42=25,AB2=25,
∴AO2+OB2=AB2,
∴∠AOB=90°,
∴AC⊥DB,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD=5,AC=2AO=6,BD=2BO=8.
.
答:其他各边的长都是5,两条对角线的长分别为6,8.
14.∠ACB=21°,∠CAB=34°
【解析】解:∵四边形ABCD是平行四边形,∠ADC=125°,
∴AD//CB,AB∥CD,∠B=∠ADC=125°,
∴∠ACB=∠CAD,
∵∠CAD=21°,
∴∠ACB=21°,
在△ABC中,∠CAB=180°-∠B-∠ACB=180°-125°-21°=34°,
15.见解析
【解析】证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
16.(1)见解析;(2)见解析.
【解析】(1)分别以A,C为圆心,BC,AB为半径画弧,两弧交于点D,连接CD,AD即可.
(2)连接CO,延长CO到C′,使得OC′=OC.同理作出点B′,A′,连接A′B′,B′C′,C′A′即可.
17.(1)它们的共同特点是都经过的中心,即对角线的交点;(2)中心对称图形中,过对称中心的任意一条直线把图形分为全等的两部分.
【解析】解:(1)如下图:这些直线都经过平行四边形两条对角线的交点O,可以看到,过点O的任意一条直线都可将平行四边形分成全等的两部分.
(2)如上图,直线AC将 分成两部分,将绕点O逆时针或是顺时针旋转可与相互重合,所以中心对称图形中,过对称中心的任意一条直线把图形分为全等的两部分.
18.(1)4 (2)40
【解析】(1)∵在□ABCD中,AB∥CD,∴∠B=180°-120°=60°
在直角三角形ABH中,AH=AB sin=8×=。
(2)S平行四边形ABCD=BC AH=。
试卷第2页,共3页
试卷第1页,共1页
6.1平行四边形的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.平行四边形具有的特征是( )
A.四个角都是直角 B.对角线相等
C.对角线互相平分 D.四边相等
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
A.4cm,6cm B.6cm,8cm C.8cm,12cm D.20cm,30cm
3.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3)
C.(7,3) D.(8,2)
4.已知四边形是平行四边形,则下列各图中与一定不相等的是( )
A. B. C. D.
5.设D为等腰底边BC上一点,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
A.2AB B.2AB+BC C.2BC D.AB+BC
6.若平行四边形相邻两边为,,它们与对边的距离分别为,,那么等于( )
A.5∶3 B.3∶5 C.10∶3 D.3∶10
二、填空题
7.若平行四边形的一边长为6,一条对角线为8,则另一条对角线a的取值范围是________.
8.如图,中,,则的长为_________.
9.如图,在中,是对角线上一点,,,则的度数为__________。
10.如图,在中,一条边的长是8,一条对角线的长为6,那么它的另一条对角线的长的取值范围是________.
11.□ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为_____.
12.已知平行四边形的面积为144,相邻两边上的高分别为8和9,则它的周长为_____.
三、解答题
13.已知 ABCD的对角线AC与BD相交于点O,OA,OB,AB的长分别为3,4,5,求其他各边以及两条对角线的长度.
14.如图,在中,,求和的度数.
15. ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
16.如图,已知△ABC及点O,请用圆规和没有刻度的直尺完成下列作图:
(1)作平行四边形ABCD ;
(2)作出△ABC关于点O对称的△A'B'C'.
17.如图,直线可以将分成全等的两部分,这样的直线还有很多.
(1)多画几条这样的直线,看看它们有什么共同的特征;
(2)尝试用中心对称图形的性质去解释你的发现.
18.已知,如图,在□ABCD中,AB=8cm,BC=10cm,∠C=120°,
(1)求BC边上的高AH的长;
(2)求□ABCD的面积。
参考答案
1.C
【解析】平行四边形对角线互相平分,对边平行且相等,对角相等.
故选C
2.D
【解析】解:由平行四边形的对角线互相平分,可得:
A、∵2+3<10, 不能构成三角形,故不符合题意;
B、 4+3<10, 不能构成三角形,故不符合题意;
C、 4+6=10, 不能构成三角形,故不符合题意;
D、 >15, 能构成三角形,故符合题意;
故选:D.
3.C
【解析】解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),
∵AB在x轴上,
∴点C与点D的纵坐标相等,都为3,
∵D点相对于A点横坐标移动了2-0=2,
∴C点横坐标为2+5=7,
∴即顶点C的坐标(7,3).
故选:C.
4.C
【解析】解:A正确;
∵∠1和∠2是对顶角,
∴∠1=∠2;
B、D正确;
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,
∴∠1=∠2;
C不正确;
∵四边形ABCD是平行四边形,
∴∠1=∠BCE,
∵∠2=∠CBE+∠BCE,
∴∠2=∠CBE+∠1,
∴∠2>∠1,即一定不相等;
故选:C.
5.A
【解析】解:∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∴DE=AF,AE=DF,
∵DF∥AC,
∴∠C=∠FDB,
∵AB=AC,
∴∠B=∠C
∴∠FDB=∠B,
∴BF=DF,
∴BF=DF=AE,
∴四边形AFDE的周长等于AE+DE+DF+AF=BF+AF+BF+AF=2AB.
故选:A
6.A
【解析】解:∵,
∴
故选:A
7.
【解析】解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC=AC=4,OB=OD=BD,
在△BOC中,BC=6,OC=4,
∴OB的取值范围是BC OC<OB<BC+OC,
即2<OB<10,
∴BD的取值范围是4<BD<20.
故答案为:.
8.
【解析】解:
故答案为:
9.21°
【解析】设.
∵,
∴,
∴.
∵.∴.
∵四边形是平行四边形,∴,
∴,
∴.
∴,解得.
即.
故答案为:21°.
10.
【解析】∵四边形是平行四边形,
∴.
在中,由三角形的三边关系,得
,
即,
∴,
∴,
即.
故答案为:.
11.
【解析】如图,过点A作AE⊥BC于点E、AF⊥CD于F,则AE=8,
由平行四边形的面积公式=底×高,可得,解得AF=.
故答案为.
12.68
【解析】由平行四边形的面积是144,相邻两边上的高分别为8和9,即可根据平行四边形的面积公式求得其相邻两边的长144÷8=18,144÷9=16,因此可得它的周长是:18+16+18+16=68.
故答案为68.
13.其他各边的长都是5,两条对角线的长分别为6,8
【解析】解:∵OA=3,OB=4,AB=5,
∴OA2+OB2=32+42=25,AB2=25,
∴AO2+OB2=AB2,
∴∠AOB=90°,
∴AC⊥DB,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD=5,AC=2AO=6,BD=2BO=8.
.
答:其他各边的长都是5,两条对角线的长分别为6,8.
14.∠ACB=21°,∠CAB=34°
【解析】解:∵四边形ABCD是平行四边形,∠ADC=125°,
∴AD//CB,AB∥CD,∠B=∠ADC=125°,
∴∠ACB=∠CAD,
∵∠CAD=21°,
∴∠ACB=21°,
在△ABC中,∠CAB=180°-∠B-∠ACB=180°-125°-21°=34°,
15.见解析
【解析】证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,四边形DEBF是平行四边形,
∴OA=OC,OE=OF,
∴OA-OE=OC-OF,
∴AE=CF.
16.(1)见解析;(2)见解析.
【解析】(1)分别以A,C为圆心,BC,AB为半径画弧,两弧交于点D,连接CD,AD即可.
(2)连接CO,延长CO到C′,使得OC′=OC.同理作出点B′,A′,连接A′B′,B′C′,C′A′即可.
17.(1)它们的共同特点是都经过的中心,即对角线的交点;(2)中心对称图形中,过对称中心的任意一条直线把图形分为全等的两部分.
【解析】解:(1)如下图:这些直线都经过平行四边形两条对角线的交点O,可以看到,过点O的任意一条直线都可将平行四边形分成全等的两部分.
(2)如上图,直线AC将 分成两部分,将绕点O逆时针或是顺时针旋转可与相互重合,所以中心对称图形中,过对称中心的任意一条直线把图形分为全等的两部分.
18.(1)4 (2)40
【解析】(1)∵在□ABCD中,AB∥CD,∴∠B=180°-120°=60°
在直角三角形ABH中,AH=AB sin=8×=。
(2)S平行四边形ABCD=BC AH=。
试卷第2页,共3页
试卷第1页,共1页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
