苏科版2021-2022学年七年级数学下册7.2探索直线平行的性质 课时培优练习题(Word版含答案)
文档属性
| 名称 | 苏科版2021-2022学年七年级数学下册7.2探索直线平行的性质 课时培优练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 01:02:20 | ||
图片预览



文档简介
课时培优精练--7.2探索直线平行的性质
-2021-2022学年七年级数学下册 (苏科版)
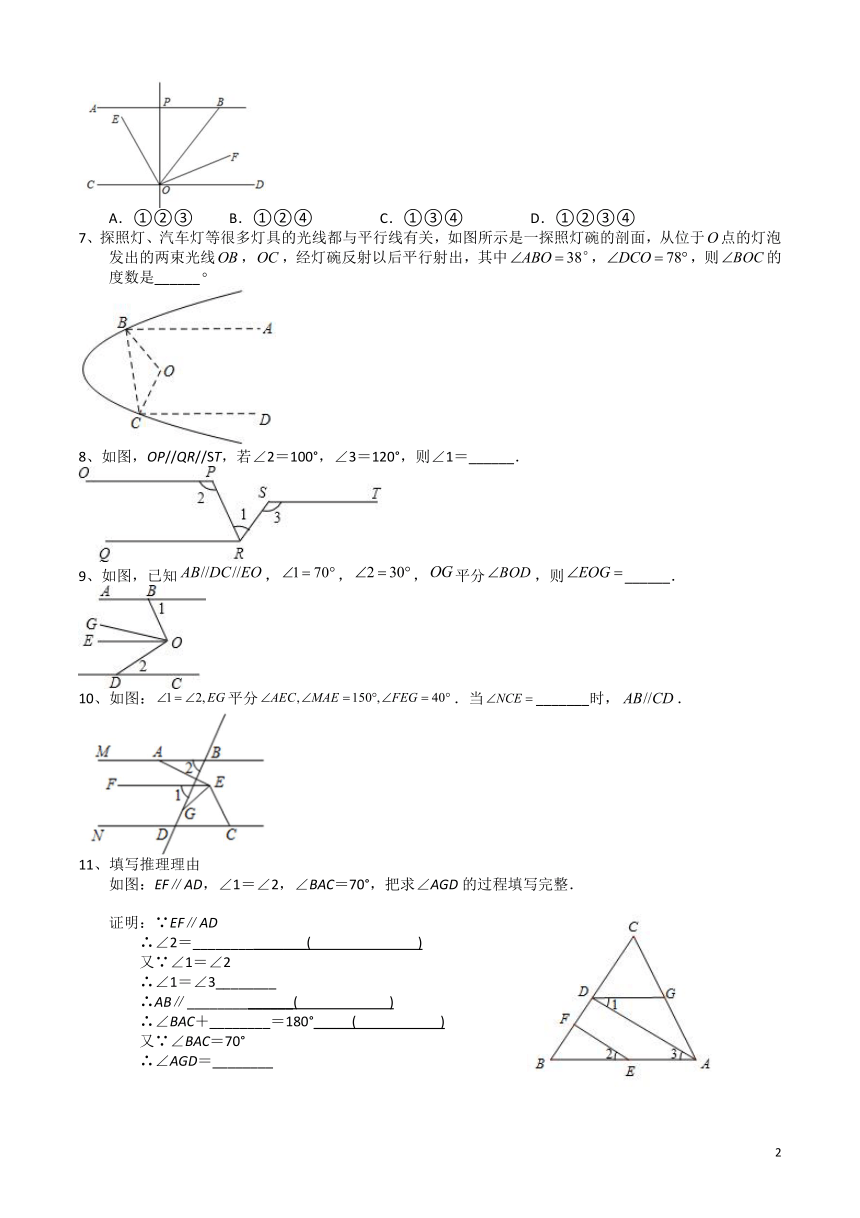
1、一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
2、如图,∠1=∠2=40°,MN平分∠EMB,则∠3= °.
3、小明和小亮在研究一道数学题,如图,,垂足分别为,,在上.
小明说:“如果,则能得到”;
小亮说:“连接,如果,则能得到”.
则下列判断正确的是
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
4、如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
5、如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6、如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
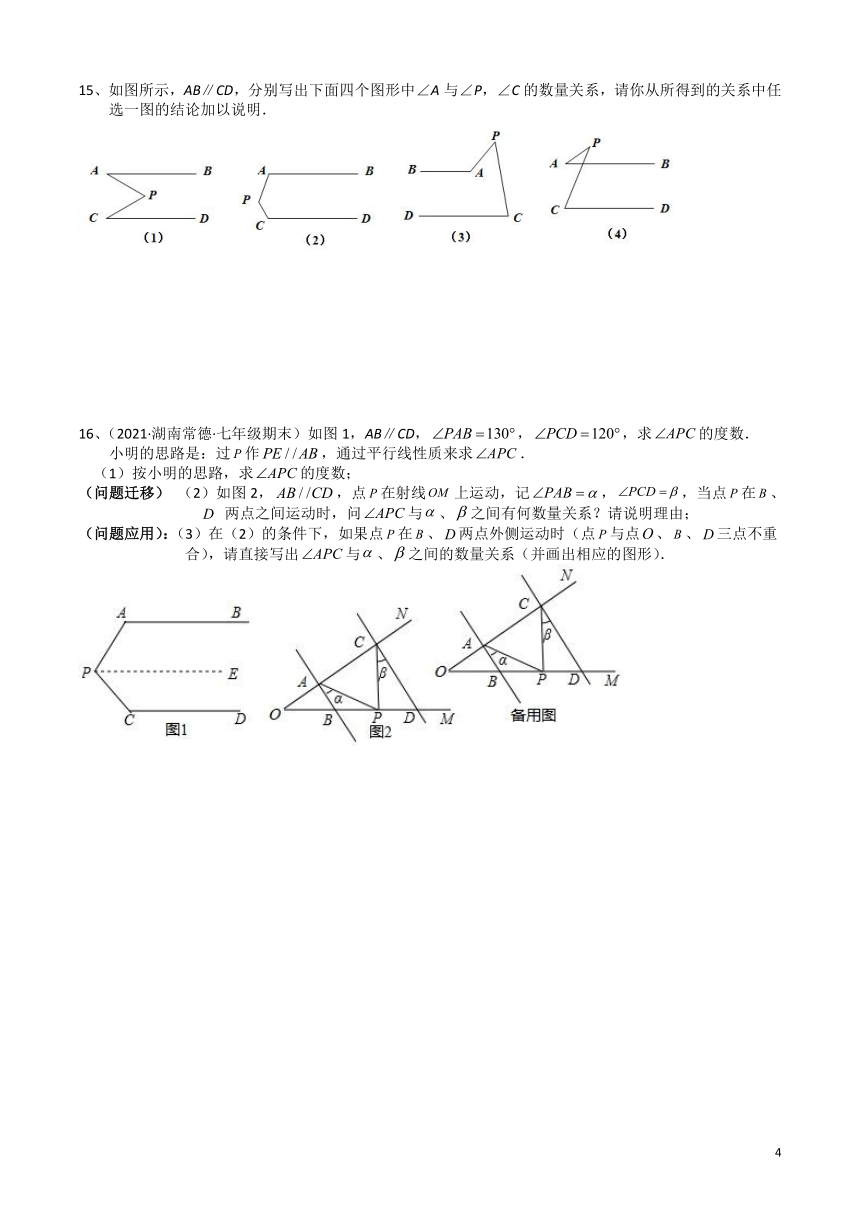
7、探照灯、汽车灯等很多灯具的光线都与平行线有关,如图所示是一探照灯碗的剖面,从位于点的灯泡发出的两束光线,,经灯碗反射以后平行射出,其中,,则的度数是______
8、如图,OP//QR//ST,若∠2=100°,∠3=120°,则∠1=______.
9、如图,已知,,,平分,则______.
10、如图:平分.当_______时,.
11、填写推理理由
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
证明:∵EF∥AD
∴∠2=_______________( )
又∵∠1=∠2
∴∠1=∠3________
∴AB∥______________( )
∴∠BAC+________=180°_____( )
又∵∠BAC=70°
∴∠AGD=________
12、如图,,分别是,上的点,,是上的点,连接,,,如果,.
(1)判断与的位置关系,并说明理由;
(2)若是的平分线,,求的度数.
13、直线和被直线MN所截,如图1,EG平分,平分,
当时,小明证明的过程如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵,(已知),
∴(等量代换).
∴(同位角相等,两直线平行).
请你参考上述证明过程解决下列问题:
(1)如图2,平分,平分,与满足什么条件时,?说明理由.
(2)如图3,若,平分,平分,则与满足怎样的条件?说明理由.
14、(2021·广东东莞·七年级期末)如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,已知.
(1)求证:AB//CD;
(2)若∠AGE+∠AHF=180°,求证:∠BFC+∠C=180°;
(3)在(2)的条件下,若∠BFC-30°=2∠C,求∠B的度数.
15、如图所示,AB∥CD,分别写出下面四个图形中∠A与∠P,∠C的数量关系,请你从所得到的关系中任选一图的结论加以说明.
16、(2021·湖南常德·七年级期末)如图1,AB∥CD,,,求的度数.
小明的思路是:过作,通过平行线性质来求.
(1)按小明的思路,求的度数;
(问题迁移) (2)如图2,,点在射线上运动,记,,当点在、 两点之间运动时,问与、之间有何数量关系?请说明理由;
(问题应用):(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系(并画出相应的图形).
课时培优精练--7.2探索直线平行的性质
-2021-2022学年七年级数学下册 (苏科版)(解析)
1、一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
【答案】B
【分析】
由题意可知∠ADF=45°,则由平行线的性质可得∠B+∠BDF=180°,求得∠BDF=150°,从而可求∠ADB的度数.
【详解】
解:由题意得∠ADF=45°,
∵,∠B=30°,
∴∠B+∠BDF=180°,
∴∠BDF=180°﹣∠B=150°,
∴∠ADB=∠BDF﹣∠ADF=105°.
故选:B
2、如图,∠1=∠2=40°,MN平分∠EMB,则∠3= °.
【分析】根据对顶角相等得出∠2=∠MEN,利用同位角相等,两直线平行得出AB∥CD,再利用平行线的性质详解即可.
【详解】解:∵∠2=∠MEN,∠1=∠2=40°,
∴∠1=∠MEN,
∴AB∥CD,
∴∠3+∠BMN=180°,
∵MN平分∠EMB,
∴∠BMN=,
∴∠3=180°﹣70°=110°.
故答案为:110.
3、小明和小亮在研究一道数学题,如图,,垂足分别为,,在上.
小明说:“如果,则能得到”;
小亮说:“连接,如果,则能得到”.
则下列判断正确的是
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
【分析】由,,知,然后根据平行线的性质与判定即可得出答案.
【解析】,,,
若,
,,,
,故小明说法正确;
,,
故得不到,故小亮说法错误,
故选:.
4、如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
【答案】C
【分析】
如图,过点C作CG∥AB,过点D作DH∥EF,根据平行线的性质可得∠A=∠ACG,∠EDH=180°﹣∠E,根据AB∥EF可得CG∥DH,根据平行线的性质可得∠CDH=∠DCG,进而根据角的和差关系即可得答案.
【详解】
如图,过点C作CG∥AB,过点D作DH∥EF,
∴∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE﹣(180°﹣∠E),
∴∠A﹣∠ACD+∠CDE+∠E=180°.
故选:C.
5、如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【分析】根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.
【详解】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β﹣α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)如图,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α﹣β.
(4)如图,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°﹣α﹣β.
∴∠AEC的度数可能为β﹣α,α+β,α﹣β,360°﹣α﹣β.
(5)当点E在CD的下方时,同理可得,∠AEC=α﹣β或β﹣α.
故选:D.
6、如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【答案】A
【分析】
根据AB∥CD可得∠BOD=∠ABO=40°,利用平角得到∠COB=140°,再根据角平分线的定义得到∠BOE=70°,则③正确;利用OP⊥CD,AB∥CD,∠ABO=40°,可得∠POB=50°,∠BOF=20°,∠FOD=20°,进而可得OF平分∠BOD,则①正确;由∠EOB=70°,∠POB=50°,∠POE=20°,由∠BOF=∠POF-∠POB=20°,进而可得∠POE=∠BOF,则②正确;由②可知∠POB=50°,∠FOD=20°,则④不正确.
【详解】
③∵AB∥CD,∴∠BOD=∠ABO=40°,∴∠COB=180°-40°=140°,
又∵OE平分∠BOC,∴∠BOE=∠COB=×140°=70°,故③正确;
①∵OP⊥CD,∴∠POD=90°,
又∵AB∥CD,∴∠BPO=90°,
又∵∠ABO=40°,∴∠POB=90°-40°=50°,
∴∠BOF=∠POF-∠POB=70°-50°=20°,∠FOD=40°-20°=20°,
∴OF平分∠BOD,故①正确;
②∵∠EOB=70°,∠POB=90°-40°=50°,∴∠POE=70°-50°=20°,
又∵∠BOF=∠POF-∠POB=70°-50°=20°,
∴∠POE=∠BOF,故②正确;
④由①可知∠POB=90°-40°=50°,∠FOD=40°-20°=20°,
故∠POB≠2∠DOF,故④不正确.
故结论正确的是①②③,
故选A.
7、探照灯、汽车灯等很多灯具的光线都与平行线有关,如图所示是一探照灯碗的剖面,从位于点的灯泡发出的两束光线,,经灯碗反射以后平行射出,其中,,则的度数是______
【答案】116
【解析】
【分析】
过O点作OE∥AB,则OE∥CD,利用平行线的性质,得内错角相等,从而求解.
【详解】
解:过O点作OE∥AB,则OE∥CD,
∴∠EOB=∠ABO,∠EOC=∠DCO,
∵∠ABO=38°,∠DCO=78°,
∴∠EOB=38°,∠EOC=78°,
即∠BOC=∠BOE+∠EOC=38°+78°=116°.
故答案为:116.
8、如图,OP//QR//ST,若∠2=100°,∠3=120°,则∠1=______.
【答案】40°
【解析】
【分析】
根据平行线的性质得到,,求出∠PRQ的度数,根据∠1=∠SRQ﹣∠PRQ代入即可求出答案.
【详解】
解:∵,,,
∴,,
∴,
∴,
故答案是40°.
9、如图,已知,,,平分,则______.
【答案】
【解析】
解:∵AB∥OE∥CD
∴∠1=∠BOE=70°,∠2=∠EOD=30°
∴∠BOD=∠EOD+∠EOB=100°
∵OG平分∠BOD
∴∠BOG==50°
∴∠GOE=∠EOD-∠BOG=20°
故答案为:20°.
10、如图:平分.当_______时,.
【答案】70°
【解析】
解:∵∠1=∠2,
∴AB∥EF,
∴∠FEA+∠MAE=180°,∠MAE=150°,
∴∠FEA=30°,∠FEG=40°,
∴∠AEG=70°,
∵EG平分∠AEC,
∴∠CEG=∠AEG=70°,
∴∠FEC=110°,
∵AB∥CD,
∴EF∥CD,
∴∠NCE+∠FEC=180°,
∴∠NCE=70°.
故答案为:70°.
11、填写推理理由
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
证明:∵EF∥AD
∴∠2=_______________( )
又∵∠1=∠2
∴∠1=∠3________
∴AB∥______________( )
∴∠BAC+________=180°_____( )
又∵∠BAC=70°
∴∠AGD=________
【答案】 ∠3 两直线平行,同位角相等 等量代换 DG 内错角相等,两直线平行 ∠AGD 两直线平行,同旁内角互补 110°##110度
【解析】
【分析】
根据平行线的判定与性质,求解即可.
【详解】
∵EF∥AD,
∴∠2=∠3,(两直线平行,同位角相等)
又∵∠1=∠2,
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,
∴∠AGD=110°.
故答案是:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°
12、如图,,分别是,上的点,,是上的点,连接,,,如果,.
(1)判断与的位置关系,并说明理由;
(2)若是的平分线,,求的度数.
【答案】(1)平行关系;(2).
【解析】
【分析】
(1)根据平行线的判定定理,结合平行线的性质定理进行判断即可;
(2)根据平行线的性质定理,结合角平分线的定义进行求解即可.
【详解】
(1)与是平行位置关系,理由如下:
因为,所以,
又因为,所以,因此;
(2)因为,,所以,
又因为是的平分线,所以,
而,所以.
13、直线和被直线MN所截,如图1,EG平分,平分,当时,小明证明的过程如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵,(已知),
∴(等量代换).
∴(同位角相等,两直线平行).
请你参考上述证明过程解决下列问题:
(1)如图2,平分,平分,与满足什么条件时,?说明理由.
(2)如图3,若,平分,平分,则与满足怎样的条件?说明理由.
【答案】(1)当时,,理由见解析;(2)当时,,理由见解析.
【解析】
解:(1)当时,.理由如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵时(已知),
∴.(等量代换).
∴(内错角相等,两直线平行).
(2)当时,.理由如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵(已知),
∴(两直线平行,同旁内角互补).
∵,(对顶角相等),
∴(等量代换).
∴.
即(等式的性质).
∴(等量代换).
14、(2021·广东东莞·七年级期末)如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,已知.
(1)求证:AB//CD;
(2)若∠AGE+∠AHF=180°,求证:∠BFC+∠C=180°;
(3)在(2)的条件下,若∠BFC-30°=2∠C,求∠B的度数.
【答案】(1)见解析;(2)见解析;(3)50°
【解析】
【分析】
(1)根据,以及对顶角,进而可得,即可证明AB//CD;
(2)根据以及已知条件证明,即可证明∠BFC+∠C=180°;
【详解】
(1),
又,
,
AB//CD;
(2),∠AGE+∠AHF=180°,
,
,
∠BFC+∠C=180°;
(3)∠BFC-30°=2∠C,
由(2)可知,∠BFC+∠C=180°,
解得,,
AB//CD,
.
15、如图所示,AB∥CD,分别写出下面四个图形中∠A与∠P,∠C的数量关系,请你从所得到的关系中任选一图的结论加以说明.
【答案】(1)∠A+∠C=∠P;(2)∠A+∠P+∠C=360°;(3)∠A=∠P+∠C;(4)∠C=∠P+∠A,证明见解析
【解析】
解:(1)∠A+∠C=∠P;证明如下:
如图所示,作PE∥AB,则PE∥CD,
∴∠A=∠1,∠C=∠2,
∵∠APC=∠1+∠2,
∴∠APC=∠A+∠C,
即:∠A+∠C=∠P;
(2)∠A+∠P+∠C=360°;证明如下:
如图所示,作PE∥AB,则PE∥CD,
∴∠A+∠1=180°,∠C+∠2=180°,
∴∠A+∠C+∠1+∠2=360°,
∵∠APC=∠1+∠2,
∴∠A+∠C+∠APC=360°,
即:∠A+∠P+∠C=360°;
(3)∠A=∠P+∠C;证明如下:
如图所示,作PH∥AB ,则PH∥CD,
∴∠HPA+∠A=180°,
∴∠HPA=180°-∠A,
∵∠HPA+∠APC+∠C=180°,
∴180°-∠A+∠P+∠C=180°,
即:∠A=∠P+∠C;
(4)∠C=∠P+∠A;证明如下:
如图所示,作PE∥AB,则PE∥CD,
∴∠EPC=∠C,∠EPA=∠A,
∵∠APC=∠EPC-∠EPA,
∴∠APC=∠C-∠A,
即:∠C=∠P+∠A.
16、(2021·湖南常德·七年级期末)如图1,AB∥CD,,,求的度数.
小明的思路是:过作,通过平行线性质来求.
(1)按小明的思路,求的度数;
(问题迁移) (2)如图2,,点在射线上运动,记,,当点在、 两点之间运动时,问与、之间有何数量关系?请说明理由;
(问题应用):(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系(并画出相应的图形).
【答案】(1)110°;(2)∠APC=α+β,理由见解答;(3)∠CPA=α﹣β或∠CPA=β﹣α.
【解析】
【分析】
(1)通过平行线性质可得∠A+∠APE=180°,∠C+∠CPE=180°,再代入∠PAB=130°,∠PCD=120°可求∠APC即可;
(2)过P作PE∥AB交AC于E,推出AB∥PE∥DC,根据平行线的性质得出α=∠APE,β=∠CPE,即可得出答案;
(3)分两种情况:P在BD延长线上;P在DB延长线上,分别画出图形,根据平行线的性质得出α=∠APE,β=∠CPE,即可得出答案.
【详解】
解:(1)过点P作PE∥AB,
∵AB∥CD,∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=α+β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,∴AB∥PE∥CD,
∴α=∠APE,β=∠CPE,∴∠APC=∠APE+∠CPE=α+β;
(3)如图所示,当P在BD延长线上时,
过点P作PE∥CD交ON于E,则PE∥AB,
∴∠APE=α,∠CPE=β,∴∠CPA=∠APE-∠CPE=α-β;
如图所示,当P在DB延长线上时,
过点P作PE∥CD交ON于E,则PE∥AB,
∴∠CPE=β,∠APE=α,∴∠CPA=∠CPE-∠APE=β-α.
-2021-2022学年七年级数学下册 (苏科版)
1、一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
2、如图,∠1=∠2=40°,MN平分∠EMB,则∠3= °.
3、小明和小亮在研究一道数学题,如图,,垂足分别为,,在上.
小明说:“如果,则能得到”;
小亮说:“连接,如果,则能得到”.
则下列判断正确的是
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
4、如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
5、如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6、如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
7、探照灯、汽车灯等很多灯具的光线都与平行线有关,如图所示是一探照灯碗的剖面,从位于点的灯泡发出的两束光线,,经灯碗反射以后平行射出,其中,,则的度数是______
8、如图,OP//QR//ST,若∠2=100°,∠3=120°,则∠1=______.
9、如图,已知,,,平分,则______.
10、如图:平分.当_______时,.
11、填写推理理由
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
证明:∵EF∥AD
∴∠2=_______________( )
又∵∠1=∠2
∴∠1=∠3________
∴AB∥______________( )
∴∠BAC+________=180°_____( )
又∵∠BAC=70°
∴∠AGD=________
12、如图,,分别是,上的点,,是上的点,连接,,,如果,.
(1)判断与的位置关系,并说明理由;
(2)若是的平分线,,求的度数.
13、直线和被直线MN所截,如图1,EG平分,平分,
当时,小明证明的过程如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵,(已知),
∴(等量代换).
∴(同位角相等,两直线平行).
请你参考上述证明过程解决下列问题:
(1)如图2,平分,平分,与满足什么条件时,?说明理由.
(2)如图3,若,平分,平分,则与满足怎样的条件?说明理由.
14、(2021·广东东莞·七年级期末)如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,已知.
(1)求证:AB//CD;
(2)若∠AGE+∠AHF=180°,求证:∠BFC+∠C=180°;
(3)在(2)的条件下,若∠BFC-30°=2∠C,求∠B的度数.
15、如图所示,AB∥CD,分别写出下面四个图形中∠A与∠P,∠C的数量关系,请你从所得到的关系中任选一图的结论加以说明.
16、(2021·湖南常德·七年级期末)如图1,AB∥CD,,,求的度数.
小明的思路是:过作,通过平行线性质来求.
(1)按小明的思路,求的度数;
(问题迁移) (2)如图2,,点在射线上运动,记,,当点在、 两点之间运动时,问与、之间有何数量关系?请说明理由;
(问题应用):(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系(并画出相应的图形).
课时培优精练--7.2探索直线平行的性质
-2021-2022学年七年级数学下册 (苏科版)(解析)
1、一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
【答案】B
【分析】
由题意可知∠ADF=45°,则由平行线的性质可得∠B+∠BDF=180°,求得∠BDF=150°,从而可求∠ADB的度数.
【详解】
解:由题意得∠ADF=45°,
∵,∠B=30°,
∴∠B+∠BDF=180°,
∴∠BDF=180°﹣∠B=150°,
∴∠ADB=∠BDF﹣∠ADF=105°.
故选:B
2、如图,∠1=∠2=40°,MN平分∠EMB,则∠3= °.
【分析】根据对顶角相等得出∠2=∠MEN,利用同位角相等,两直线平行得出AB∥CD,再利用平行线的性质详解即可.
【详解】解:∵∠2=∠MEN,∠1=∠2=40°,
∴∠1=∠MEN,
∴AB∥CD,
∴∠3+∠BMN=180°,
∵MN平分∠EMB,
∴∠BMN=,
∴∠3=180°﹣70°=110°.
故答案为:110.
3、小明和小亮在研究一道数学题,如图,,垂足分别为,,在上.
小明说:“如果,则能得到”;
小亮说:“连接,如果,则能得到”.
则下列判断正确的是
A.小明说法正确,小亮说法错误 B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确 D.小明说法错误,小亮说法错误
【分析】由,,知,然后根据平行线的性质与判定即可得出答案.
【解析】,,,
若,
,,,
,故小明说法正确;
,,
故得不到,故小亮说法错误,
故选:.
4、如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
【答案】C
【分析】
如图,过点C作CG∥AB,过点D作DH∥EF,根据平行线的性质可得∠A=∠ACG,∠EDH=180°﹣∠E,根据AB∥EF可得CG∥DH,根据平行线的性质可得∠CDH=∠DCG,进而根据角的和差关系即可得答案.
【详解】
如图,过点C作CG∥AB,过点D作DH∥EF,
∴∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE﹣(180°﹣∠E),
∴∠A﹣∠ACD+∠CDE+∠E=180°.
故选:C.
5、如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【分析】根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.
【详解】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β﹣α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)如图,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α﹣β.
(4)如图,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°﹣α﹣β.
∴∠AEC的度数可能为β﹣α,α+β,α﹣β,360°﹣α﹣β.
(5)当点E在CD的下方时,同理可得,∠AEC=α﹣β或β﹣α.
故选:D.
6、如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【答案】A
【分析】
根据AB∥CD可得∠BOD=∠ABO=40°,利用平角得到∠COB=140°,再根据角平分线的定义得到∠BOE=70°,则③正确;利用OP⊥CD,AB∥CD,∠ABO=40°,可得∠POB=50°,∠BOF=20°,∠FOD=20°,进而可得OF平分∠BOD,则①正确;由∠EOB=70°,∠POB=50°,∠POE=20°,由∠BOF=∠POF-∠POB=20°,进而可得∠POE=∠BOF,则②正确;由②可知∠POB=50°,∠FOD=20°,则④不正确.
【详解】
③∵AB∥CD,∴∠BOD=∠ABO=40°,∴∠COB=180°-40°=140°,
又∵OE平分∠BOC,∴∠BOE=∠COB=×140°=70°,故③正确;
①∵OP⊥CD,∴∠POD=90°,
又∵AB∥CD,∴∠BPO=90°,
又∵∠ABO=40°,∴∠POB=90°-40°=50°,
∴∠BOF=∠POF-∠POB=70°-50°=20°,∠FOD=40°-20°=20°,
∴OF平分∠BOD,故①正确;
②∵∠EOB=70°,∠POB=90°-40°=50°,∴∠POE=70°-50°=20°,
又∵∠BOF=∠POF-∠POB=70°-50°=20°,
∴∠POE=∠BOF,故②正确;
④由①可知∠POB=90°-40°=50°,∠FOD=40°-20°=20°,
故∠POB≠2∠DOF,故④不正确.
故结论正确的是①②③,
故选A.
7、探照灯、汽车灯等很多灯具的光线都与平行线有关,如图所示是一探照灯碗的剖面,从位于点的灯泡发出的两束光线,,经灯碗反射以后平行射出,其中,,则的度数是______
【答案】116
【解析】
【分析】
过O点作OE∥AB,则OE∥CD,利用平行线的性质,得内错角相等,从而求解.
【详解】
解:过O点作OE∥AB,则OE∥CD,
∴∠EOB=∠ABO,∠EOC=∠DCO,
∵∠ABO=38°,∠DCO=78°,
∴∠EOB=38°,∠EOC=78°,
即∠BOC=∠BOE+∠EOC=38°+78°=116°.
故答案为:116.
8、如图,OP//QR//ST,若∠2=100°,∠3=120°,则∠1=______.
【答案】40°
【解析】
【分析】
根据平行线的性质得到,,求出∠PRQ的度数,根据∠1=∠SRQ﹣∠PRQ代入即可求出答案.
【详解】
解:∵,,,
∴,,
∴,
∴,
故答案是40°.
9、如图,已知,,,平分,则______.
【答案】
【解析】
解:∵AB∥OE∥CD
∴∠1=∠BOE=70°,∠2=∠EOD=30°
∴∠BOD=∠EOD+∠EOB=100°
∵OG平分∠BOD
∴∠BOG==50°
∴∠GOE=∠EOD-∠BOG=20°
故答案为:20°.
10、如图:平分.当_______时,.
【答案】70°
【解析】
解:∵∠1=∠2,
∴AB∥EF,
∴∠FEA+∠MAE=180°,∠MAE=150°,
∴∠FEA=30°,∠FEG=40°,
∴∠AEG=70°,
∵EG平分∠AEC,
∴∠CEG=∠AEG=70°,
∴∠FEC=110°,
∵AB∥CD,
∴EF∥CD,
∴∠NCE+∠FEC=180°,
∴∠NCE=70°.
故答案为:70°.
11、填写推理理由
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
证明:∵EF∥AD
∴∠2=_______________( )
又∵∠1=∠2
∴∠1=∠3________
∴AB∥______________( )
∴∠BAC+________=180°_____( )
又∵∠BAC=70°
∴∠AGD=________
【答案】 ∠3 两直线平行,同位角相等 等量代换 DG 内错角相等,两直线平行 ∠AGD 两直线平行,同旁内角互补 110°##110度
【解析】
【分析】
根据平行线的判定与性质,求解即可.
【详解】
∵EF∥AD,
∴∠2=∠3,(两直线平行,同位角相等)
又∵∠1=∠2,
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,
∴∠AGD=110°.
故答案是:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°
12、如图,,分别是,上的点,,是上的点,连接,,,如果,.
(1)判断与的位置关系,并说明理由;
(2)若是的平分线,,求的度数.
【答案】(1)平行关系;(2).
【解析】
【分析】
(1)根据平行线的判定定理,结合平行线的性质定理进行判断即可;
(2)根据平行线的性质定理,结合角平分线的定义进行求解即可.
【详解】
(1)与是平行位置关系,理由如下:
因为,所以,
又因为,所以,因此;
(2)因为,,所以,
又因为是的平分线,所以,
而,所以.
13、直线和被直线MN所截,如图1,EG平分,平分,当时,小明证明的过程如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵,(已知),
∴(等量代换).
∴(同位角相等,两直线平行).
请你参考上述证明过程解决下列问题:
(1)如图2,平分,平分,与满足什么条件时,?说明理由.
(2)如图3,若,平分,平分,则与满足怎样的条件?说明理由.
【答案】(1)当时,,理由见解析;(2)当时,,理由见解析.
【解析】
解:(1)当时,.理由如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵时(已知),
∴.(等量代换).
∴(内错角相等,两直线平行).
(2)当时,.理由如下:
∵平分,平分(已知),
∴,(角平分线的定义).
∵(已知),
∴(两直线平行,同旁内角互补).
∵,(对顶角相等),
∴(等量代换).
∴.
即(等式的性质).
∴(等量代换).
14、(2021·广东东莞·七年级期末)如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,已知.
(1)求证:AB//CD;
(2)若∠AGE+∠AHF=180°,求证:∠BFC+∠C=180°;
(3)在(2)的条件下,若∠BFC-30°=2∠C,求∠B的度数.
【答案】(1)见解析;(2)见解析;(3)50°
【解析】
【分析】
(1)根据,以及对顶角,进而可得,即可证明AB//CD;
(2)根据以及已知条件证明,即可证明∠BFC+∠C=180°;
【详解】
(1),
又,
,
AB//CD;
(2),∠AGE+∠AHF=180°,
,
,
∠BFC+∠C=180°;
(3)∠BFC-30°=2∠C,
由(2)可知,∠BFC+∠C=180°,
解得,,
AB//CD,
.
15、如图所示,AB∥CD,分别写出下面四个图形中∠A与∠P,∠C的数量关系,请你从所得到的关系中任选一图的结论加以说明.
【答案】(1)∠A+∠C=∠P;(2)∠A+∠P+∠C=360°;(3)∠A=∠P+∠C;(4)∠C=∠P+∠A,证明见解析
【解析】
解:(1)∠A+∠C=∠P;证明如下:
如图所示,作PE∥AB,则PE∥CD,
∴∠A=∠1,∠C=∠2,
∵∠APC=∠1+∠2,
∴∠APC=∠A+∠C,
即:∠A+∠C=∠P;
(2)∠A+∠P+∠C=360°;证明如下:
如图所示,作PE∥AB,则PE∥CD,
∴∠A+∠1=180°,∠C+∠2=180°,
∴∠A+∠C+∠1+∠2=360°,
∵∠APC=∠1+∠2,
∴∠A+∠C+∠APC=360°,
即:∠A+∠P+∠C=360°;
(3)∠A=∠P+∠C;证明如下:
如图所示,作PH∥AB ,则PH∥CD,
∴∠HPA+∠A=180°,
∴∠HPA=180°-∠A,
∵∠HPA+∠APC+∠C=180°,
∴180°-∠A+∠P+∠C=180°,
即:∠A=∠P+∠C;
(4)∠C=∠P+∠A;证明如下:
如图所示,作PE∥AB,则PE∥CD,
∴∠EPC=∠C,∠EPA=∠A,
∵∠APC=∠EPC-∠EPA,
∴∠APC=∠C-∠A,
即:∠C=∠P+∠A.
16、(2021·湖南常德·七年级期末)如图1,AB∥CD,,,求的度数.
小明的思路是:过作,通过平行线性质来求.
(1)按小明的思路,求的度数;
(问题迁移) (2)如图2,,点在射线上运动,记,,当点在、 两点之间运动时,问与、之间有何数量关系?请说明理由;
(问题应用):(3)在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系(并画出相应的图形).
【答案】(1)110°;(2)∠APC=α+β,理由见解答;(3)∠CPA=α﹣β或∠CPA=β﹣α.
【解析】
【分析】
(1)通过平行线性质可得∠A+∠APE=180°,∠C+∠CPE=180°,再代入∠PAB=130°,∠PCD=120°可求∠APC即可;
(2)过P作PE∥AB交AC于E,推出AB∥PE∥DC,根据平行线的性质得出α=∠APE,β=∠CPE,即可得出答案;
(3)分两种情况:P在BD延长线上;P在DB延长线上,分别画出图形,根据平行线的性质得出α=∠APE,β=∠CPE,即可得出答案.
【详解】
解:(1)过点P作PE∥AB,
∵AB∥CD,∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=α+β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,∴AB∥PE∥CD,
∴α=∠APE,β=∠CPE,∴∠APC=∠APE+∠CPE=α+β;
(3)如图所示,当P在BD延长线上时,
过点P作PE∥CD交ON于E,则PE∥AB,
∴∠APE=α,∠CPE=β,∴∠CPA=∠APE-∠CPE=α-β;
如图所示,当P在DB延长线上时,
过点P作PE∥CD交ON于E,则PE∥AB,
∴∠CPE=β,∠APE=α,∴∠CPA=∠CPE-∠APE=β-α.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
