苏科版2021-2022学年七年级数学下册7.1探索直线平行的条件 课时培优练习题(Word版含答案)
文档属性
| 名称 | 苏科版2021-2022学年七年级数学下册7.1探索直线平行的条件 课时培优练习题(Word版含答案) |

|
|
| 格式 | doc | ||
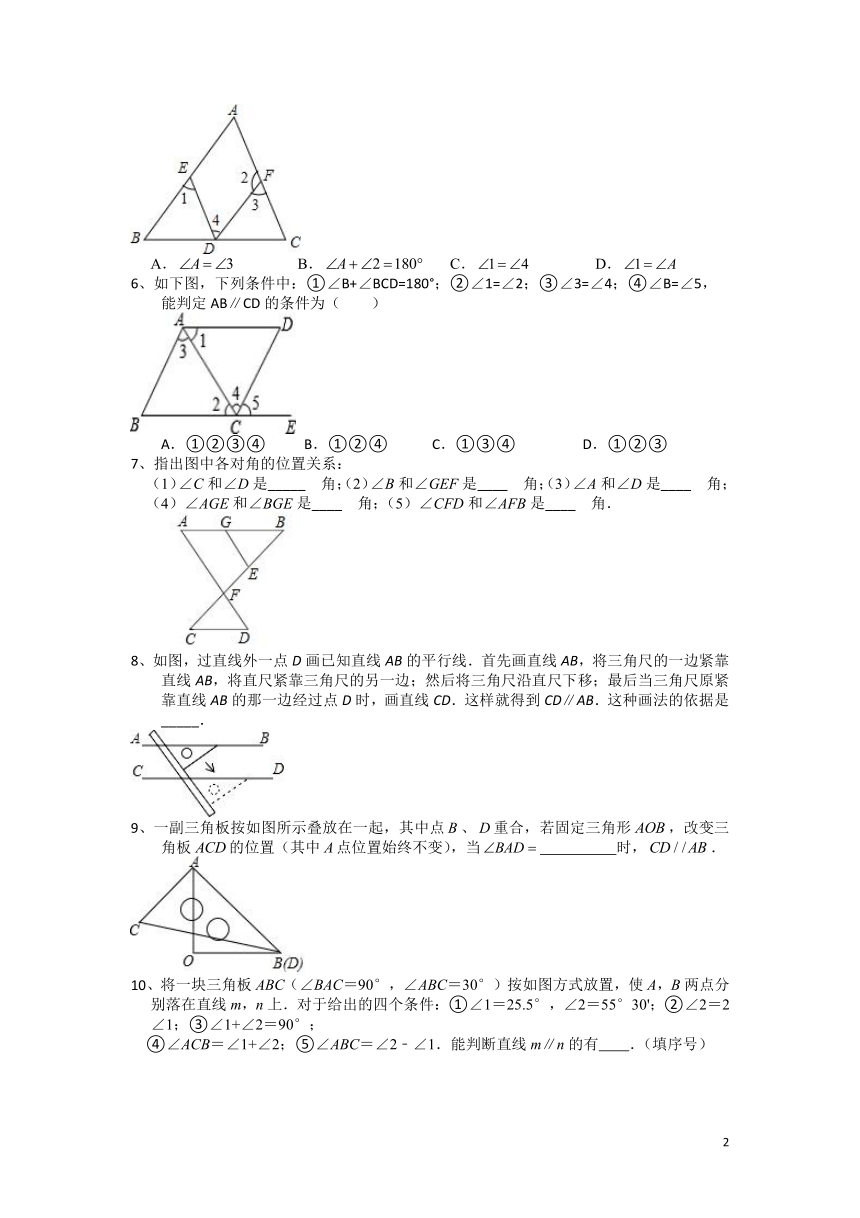
| 文件大小 | 974.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 00:00:00 | ||
图片预览



文档简介
课时培优精练--7.1探索直线平行的条件
-2021-2022学年七年级数学下册 (苏科版)
1、如图,下列判断正确的是
A.与是内错角 B.与是同位角
C.与是同位角 D.与是对顶角
2、如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
3、如图所示,下列说法:
①与是同位角; ②与是内错角;③与是同旁内角;
④与是同旁内角. 其中正确的是
A.①②③ B.②③④ C.①③④ D.①②④
4、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
5、如图,在下列给出的条件中,不能判定的是
A. B. C. D.
6、如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定AB∥CD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
7、指出图中各对角的位置关系:
(1)∠C和∠D是_____ 角;(2)∠B和∠GEF是____ 角;(3)∠A和∠D是____ 角;
(4)∠AGE和∠BGE是____ 角;(5)∠CFD和∠AFB是____ 角.
8、如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是_____.
9、一副三角板按如图所示叠放在一起,其中点、重合,若固定三角形,改变三角板的位置(其中点位置始终不变),当 时,.
10、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
11、补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
12、完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( ).
∵平分(已知),
∴________( ).
∴( ).
∵(已知),
∴________( ).
∴( ).
13、如图,,,垂足分别是、点,.
(1) 判断与的位置关系;
(2)与平行吗?为什么?
14、如图,若∠1 +∠MEN + ∠2 = 360 ,求证:AB//CD.
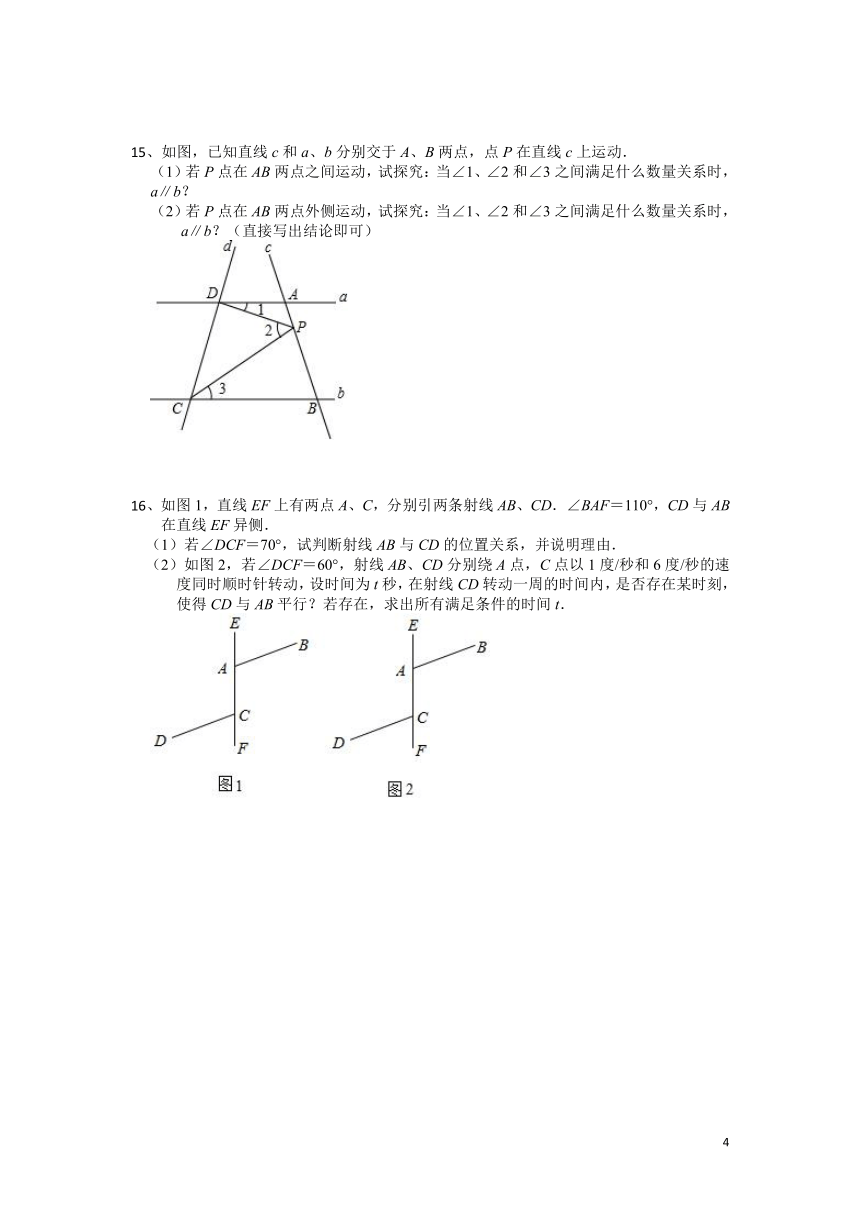
15、如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
(1)若P点在AB两点之间运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?
(2)若P点在AB两点外侧运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?(直接写出结论即可)
16、如图1,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB在直线EF异侧.
(1)若∠DCF=70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图2,若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
课时培优精练--7.1探索直线平行的条件
-2021-2022学年七年级数学下册 (苏科版)(解析)
1、如图,下列判断正确的是
A.与是内错角 B.与是同位角
C.与是同位角 D.与是对顶角
【分析】根据同位角、内错角、同旁内角、对顶角的意义进行判断即可.
【解析】与不是两条直线被第三条直线所截的同位角、内错角、同旁内角,因此选项不符合题意;
同理与既不是同位角、内错角,也不是同旁内角,因此选项不符合题意;
与是直线,直线被直线所截的同旁内角,因此选项不符合题意;
和是直线,直线相交所得的对顶角,因此选项符合题意;
故选:.
2、如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
【答案】C
【分析】
根据同位角的定义,进行分析求解即可得到答案.
【详解】
解:如图所示
由AB、CD、EF组成的“三线八角”中同位角有四对;
射线GM和直线CD被直线EF所截,形成2对同位角;
射线GM和直线HN被直线EF所截,形成2对同位角;
射线HN和直线AB被直线EF所截,形成2对同位角.
则总共10对.
故选C.
3、如图所示,下列说法:
①与是同位角; ②与是内错角;③与是同旁内角;
④与是同旁内角. 其中正确的是
A.①②③ B.②③④ C.①③④ D.①②④
【分析】利用同位角、内错角、同旁内角定义进行解答即可.
【解析】①与是同位角,说法正确;
②与是内错角,说法错误;
③与是同旁内角,说法正确;
④与是同旁内角,说法正确;
故选:.
4、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
【分析】根据平行线的判定定理,对各小题进行逐一判断即可.
【详解】解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
5、如图,在下列给出的条件中,不能判定的是
A. B. C. D.
【分析】利用平行线的判定定理,逐一判断,容易得出结论.
【解析】、因为,所以(同位角相等,两直线平行),故本选项不符合题意.
、因为,所以(同旁内角互补,两直线平行),故本选项不符合题意.
、因为,所以(内错角相等,两直线平行),故本选项不符合题意.
、因为,所以(同位角相等,两直线平行),不能证出,故本选项符合题意.
故选:.
6、如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定AB∥CD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
【答案】C
【详解】
解:①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
故选C.
7、指出图中各对角的位置关系:
(1)∠C和∠D是_____ 角;(2)∠B和∠GEF是____ 角;(3)∠A和∠D是____ 角;
(4)∠AGE和∠BGE是____ 角;(5)∠CFD和∠AFB是____ 角.
【答案】同旁内 同位 内错 邻补 对顶
【分析】
根据同位角,同旁内角,内错角,邻补角,对顶角的定义进行逐一判断即可.
【详解】
解:(1)∠C和∠D是同旁内角;
(2)∠B和∠GEF是同位角;
(3)∠A和∠D是内错角;
(4)∠AGE和∠BGE是邻补角;
(5)∠CFD和∠AFB是对顶角;
故答案为:(1)同旁内 (2)同位 (3)内错 (4)邻补(5)对顶.
8、如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是_____.
【答案】同位角相等两直线平行.
【解析】
【分析】
根据同位角相等两直线平行解答即可.
【详解】
如图,由画法可知∠BEF=∠DFG,
∴AB∥CD(同位角相等两直线平行),
故答案为:同位角相等两直线平行.
9、一副三角板按如图所示叠放在一起,其中点、重合,若固定三角形,改变三角板的位置(其中点位置始终不变),当 时,.
【分析】分两种情况,根据,利用平行线的性质,即可得到的度数.
【解析】如图所示:当时,;
如图所示,当时,,
;
故答案为:或.
10、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
【分析】根据平行线的判定详解即可.
【详解】解:①∵∠1=25.5°,∠ABC=30°,
∴∠2=∠1+∠ABC=55.5°=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
11、补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
【分析】由已知CE平分∠BCD可得∠1= ∠4,利用等式的性质得出∠1=∠2=∠4=70°,根据直线判定定理得出AD∥BC,利用平角定义求出∠D=180°-∠BCD即可.
【详解】
证明:∵CE平分∠BCD( 已知 ),
∴∠1= ∠4 ( 角平分线定义 ),
∵∠1=∠2=70°已知,
∴∠1=∠2=∠4=70°(等量代换),
∴AD∥BC(内错角相等,两直线平行),
∴∠D=180°-∠BCD=180°-∠1-∠4=40°,
∵∠3=40°已知,
∴ ∠D =∠3,
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;∠4 ,角平分线定义 ;等量代换;内错角相等,两直线平行;∠BCD;∠D;内错角相等,两直线平行.
12、完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( ).
∵平分(已知),
∴________( ).
∴( ).
∵(已知),
∴________( ).
∴( ).
【答案】角的平分线的定义;;角的平分线的定义;等式性质;;等量代换;同旁内角互补,两直线平行.
【分析】
根据角平分线的性质,等式性质,等量代换,平行线判定逐个求解即可.
【详解】
解:平分(已知)
∴(角平分线的定义)
平分(已知)
∴2∠β(角平分线的定义)
∴(等式性质)
(已知)
∴180°(等量代换)
∴(同旁内角互补,两直线平行).
故答案为:角的平分线的定义;;角的平分线的定义;等式性质;;等量代换;同旁内角互补,两直线平行.
13、如图,,,垂足分别是、点,.
(1) 判断与的位置关系;
(2)与平行吗?为什么?
【分析】(1) 利用垂直于同一直线的两条直线平行来判断;
(2) 利用同位角相等来判定两直线平行 .
【解析】 (1).
,,
,
;
(2).
,,
,
即,
.
14、如图,若∠1 +∠MEN + ∠2 = 360 ,求证:AB//CD.
【答案】见解析.
【解析】
如图,过点 E 作 EF∥AB
∵EF∥AB
∴1+MEF=180
∵ MEN=MEF+NEF
1+MEN+2=360
∴1+MEF+NEF+2=360
∴NEF+2=180
∴EF∥CD ,
又∵EF∥AB
∴CD∥AB
15、如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
(1)若P点在AB两点之间运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?
(2)若P点在AB两点外侧运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?(直接写出结论即可)
【分析】(1)过P作MP∥a,根据平行线的性质可得∠1=∠DPM,然后可得∠3=∠MPC,进而得到MP∥BC,再根据平行线的传递性可得a∥b;
(2)若P点在AB两点外侧运动,∠1﹣∠3=∠2时,a∥b,证明方法与(1)相同.
【详解】解:(1)∠1+∠3=∠2时,a∥b;
过P作MP∥a,
∵MP∥a,∴∠1=∠DPM,
∵∠1+∠3=∠2,∴∠3=∠MPC,
∴MP∥BC,∴a∥b;
(2)若P点在A点上部运动时,∠3﹣∠1=∠2时,a∥b;
若P点在B点下部运动时,∠1﹣∠3=∠2时,a∥b.
16、如图1,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB在直线EF异侧.
(1)若∠DCF=70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图2,若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
【分析】
(1)根据邻补角的定义得到∠ACD=180°﹣∠DCF=110°,根据平行线的判定定理即可得到结论;
(2)分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据内错角相等两直线平行,列式计算即可得解;
②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解;
③CD旋转到与AB都在EF的左侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解.
【详解】解:(1)AB∥CD,
理由:∵∠DCF=70°,
∴∠ACD=180°﹣∠DCF=110°,
∵∠BAF=110°,∴∠BAF=∠ACD,∴AB∥CD;
(2)解:存在.分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAF,
即120°﹣(6t)°=110°﹣t°,解得t=2;
此时(180°﹣60°)÷6=20,∴0<t<20;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(6t)°=110°﹣t°,解得t=38,
此时(360°﹣60°)÷6=50,∴20<t<50;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,即(6t)°﹣300°=t°﹣110°,解得t=38,
此时t>50,
∵38<50,∴此情况不存在.
综上所述,t为2秒或38秒时,CD与AB平行.
-2021-2022学年七年级数学下册 (苏科版)
1、如图,下列判断正确的是
A.与是内错角 B.与是同位角
C.与是同位角 D.与是对顶角
2、如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
3、如图所示,下列说法:
①与是同位角; ②与是内错角;③与是同旁内角;
④与是同旁内角. 其中正确的是
A.①②③ B.②③④ C.①③④ D.①②④
4、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
5、如图,在下列给出的条件中,不能判定的是
A. B. C. D.
6、如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定AB∥CD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
7、指出图中各对角的位置关系:
(1)∠C和∠D是_____ 角;(2)∠B和∠GEF是____ 角;(3)∠A和∠D是____ 角;
(4)∠AGE和∠BGE是____ 角;(5)∠CFD和∠AFB是____ 角.
8、如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是_____.
9、一副三角板按如图所示叠放在一起,其中点、重合,若固定三角形,改变三角板的位置(其中点位置始终不变),当 时,.
10、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
11、补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
12、完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( ).
∵平分(已知),
∴________( ).
∴( ).
∵(已知),
∴________( ).
∴( ).
13、如图,,,垂足分别是、点,.
(1) 判断与的位置关系;
(2)与平行吗?为什么?
14、如图,若∠1 +∠MEN + ∠2 = 360 ,求证:AB//CD.
15、如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
(1)若P点在AB两点之间运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?
(2)若P点在AB两点外侧运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?(直接写出结论即可)
16、如图1,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB在直线EF异侧.
(1)若∠DCF=70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图2,若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
课时培优精练--7.1探索直线平行的条件
-2021-2022学年七年级数学下册 (苏科版)(解析)
1、如图,下列判断正确的是
A.与是内错角 B.与是同位角
C.与是同位角 D.与是对顶角
【分析】根据同位角、内错角、同旁内角、对顶角的意义进行判断即可.
【解析】与不是两条直线被第三条直线所截的同位角、内错角、同旁内角,因此选项不符合题意;
同理与既不是同位角、内错角,也不是同旁内角,因此选项不符合题意;
与是直线,直线被直线所截的同旁内角,因此选项不符合题意;
和是直线,直线相交所得的对顶角,因此选项符合题意;
故选:.
2、如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
【答案】C
【分析】
根据同位角的定义,进行分析求解即可得到答案.
【详解】
解:如图所示
由AB、CD、EF组成的“三线八角”中同位角有四对;
射线GM和直线CD被直线EF所截,形成2对同位角;
射线GM和直线HN被直线EF所截,形成2对同位角;
射线HN和直线AB被直线EF所截,形成2对同位角.
则总共10对.
故选C.
3、如图所示,下列说法:
①与是同位角; ②与是内错角;③与是同旁内角;
④与是同旁内角. 其中正确的是
A.①②③ B.②③④ C.①③④ D.①②④
【分析】利用同位角、内错角、同旁内角定义进行解答即可.
【解析】①与是同位角,说法正确;
②与是内错角,说法错误;
③与是同旁内角,说法正确;
④与是同旁内角,说法正确;
故选:.
4、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
【分析】根据平行线的判定定理,对各小题进行逐一判断即可.
【详解】解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
5、如图,在下列给出的条件中,不能判定的是
A. B. C. D.
【分析】利用平行线的判定定理,逐一判断,容易得出结论.
【解析】、因为,所以(同位角相等,两直线平行),故本选项不符合题意.
、因为,所以(同旁内角互补,两直线平行),故本选项不符合题意.
、因为,所以(内错角相等,两直线平行),故本选项不符合题意.
、因为,所以(同位角相等,两直线平行),不能证出,故本选项符合题意.
故选:.
6、如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,
能判定AB∥CD的条件为( )
A.①②③④ B.①②④ C.①③④ D.①②③
【答案】C
【详解】
解:①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
故选C.
7、指出图中各对角的位置关系:
(1)∠C和∠D是_____ 角;(2)∠B和∠GEF是____ 角;(3)∠A和∠D是____ 角;
(4)∠AGE和∠BGE是____ 角;(5)∠CFD和∠AFB是____ 角.
【答案】同旁内 同位 内错 邻补 对顶
【分析】
根据同位角,同旁内角,内错角,邻补角,对顶角的定义进行逐一判断即可.
【详解】
解:(1)∠C和∠D是同旁内角;
(2)∠B和∠GEF是同位角;
(3)∠A和∠D是内错角;
(4)∠AGE和∠BGE是邻补角;
(5)∠CFD和∠AFB是对顶角;
故答案为:(1)同旁内 (2)同位 (3)内错 (4)邻补(5)对顶.
8、如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是_____.
【答案】同位角相等两直线平行.
【解析】
【分析】
根据同位角相等两直线平行解答即可.
【详解】
如图,由画法可知∠BEF=∠DFG,
∴AB∥CD(同位角相等两直线平行),
故答案为:同位角相等两直线平行.
9、一副三角板按如图所示叠放在一起,其中点、重合,若固定三角形,改变三角板的位置(其中点位置始终不变),当 时,.
【分析】分两种情况,根据,利用平行线的性质,即可得到的度数.
【解析】如图所示:当时,;
如图所示,当时,,
;
故答案为:或.
10、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
【分析】根据平行线的判定详解即可.
【详解】解:①∵∠1=25.5°,∠ABC=30°,
∴∠2=∠1+∠ABC=55.5°=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
11、补全下列推理过程:已知:如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,求证:AB∥CD.
证明:∵CE平分∠BCD(______)
∴∠1=_____(_______)
∵∠1=∠2=70°(已知)
∴∠1=∠2=∠4=70°(________)
∴AD∥BC(________)
∴∠D=180°-_______=180°-∠1-∠4=40°
∵∠3=40°(已知)
∴______=∠3
∴AB∥CD(_______)
【分析】由已知CE平分∠BCD可得∠1= ∠4,利用等式的性质得出∠1=∠2=∠4=70°,根据直线判定定理得出AD∥BC,利用平角定义求出∠D=180°-∠BCD即可.
【详解】
证明:∵CE平分∠BCD( 已知 ),
∴∠1= ∠4 ( 角平分线定义 ),
∵∠1=∠2=70°已知,
∴∠1=∠2=∠4=70°(等量代换),
∴AD∥BC(内错角相等,两直线平行),
∴∠D=180°-∠BCD=180°-∠1-∠4=40°,
∵∠3=40°已知,
∴ ∠D =∠3,
∴AB∥CD(内错角相等,两直线平行).
故答案为:已知;∠4 ,角平分线定义 ;等量代换;内错角相等,两直线平行;∠BCD;∠D;内错角相等,两直线平行.
12、完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( ).
∵平分(已知),
∴________( ).
∴( ).
∵(已知),
∴________( ).
∴( ).
【答案】角的平分线的定义;;角的平分线的定义;等式性质;;等量代换;同旁内角互补,两直线平行.
【分析】
根据角平分线的性质,等式性质,等量代换,平行线判定逐个求解即可.
【详解】
解:平分(已知)
∴(角平分线的定义)
平分(已知)
∴2∠β(角平分线的定义)
∴(等式性质)
(已知)
∴180°(等量代换)
∴(同旁内角互补,两直线平行).
故答案为:角的平分线的定义;;角的平分线的定义;等式性质;;等量代换;同旁内角互补,两直线平行.
13、如图,,,垂足分别是、点,.
(1) 判断与的位置关系;
(2)与平行吗?为什么?
【分析】(1) 利用垂直于同一直线的两条直线平行来判断;
(2) 利用同位角相等来判定两直线平行 .
【解析】 (1).
,,
,
;
(2).
,,
,
即,
.
14、如图,若∠1 +∠MEN + ∠2 = 360 ,求证:AB//CD.
【答案】见解析.
【解析】
如图,过点 E 作 EF∥AB
∵EF∥AB
∴1+MEF=180
∵ MEN=MEF+NEF
1+MEN+2=360
∴1+MEF+NEF+2=360
∴NEF+2=180
∴EF∥CD ,
又∵EF∥AB
∴CD∥AB
15、如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
(1)若P点在AB两点之间运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?
(2)若P点在AB两点外侧运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?(直接写出结论即可)
【分析】(1)过P作MP∥a,根据平行线的性质可得∠1=∠DPM,然后可得∠3=∠MPC,进而得到MP∥BC,再根据平行线的传递性可得a∥b;
(2)若P点在AB两点外侧运动,∠1﹣∠3=∠2时,a∥b,证明方法与(1)相同.
【详解】解:(1)∠1+∠3=∠2时,a∥b;
过P作MP∥a,
∵MP∥a,∴∠1=∠DPM,
∵∠1+∠3=∠2,∴∠3=∠MPC,
∴MP∥BC,∴a∥b;
(2)若P点在A点上部运动时,∠3﹣∠1=∠2时,a∥b;
若P点在B点下部运动时,∠1﹣∠3=∠2时,a∥b.
16、如图1,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,CD与AB在直线EF异侧.
(1)若∠DCF=70°,试判断射线AB与CD的位置关系,并说明理由.
(2)如图2,若∠DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
【分析】
(1)根据邻补角的定义得到∠ACD=180°﹣∠DCF=110°,根据平行线的判定定理即可得到结论;
(2)分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据内错角相等两直线平行,列式计算即可得解;
②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解;
③CD旋转到与AB都在EF的左侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解.
【详解】解:(1)AB∥CD,
理由:∵∠DCF=70°,
∴∠ACD=180°﹣∠DCF=110°,
∵∠BAF=110°,∴∠BAF=∠ACD,∴AB∥CD;
(2)解:存在.分三种情况:
如图①,AB与CD在EF的两侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠ACD=180°﹣60°﹣(6t)°=120°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAF,
即120°﹣(6t)°=110°﹣t°,解得t=2;
此时(180°﹣60°)÷6=20,∴0<t<20;
②CD旋转到与AB都在EF的右侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=360°﹣(6t)°﹣60°=300°﹣(6t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(6t)°=110°﹣t°,解得t=38,
此时(360°﹣60°)÷6=50,∴20<t<50;
③CD旋转到与AB都在EF的左侧时,
∵∠BAF=110°,∠DCF=60°,
∴∠DCF=(6t)°﹣(180°﹣60°+180°)=(6t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,即(6t)°﹣300°=t°﹣110°,解得t=38,
此时t>50,
∵38<50,∴此情况不存在.
综上所述,t为2秒或38秒时,CD与AB平行.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
