2022年人教版数学七年级下册5.3 平行线的性质 同步培优(Word版含答案)
文档属性
| 名称 | 2022年人教版数学七年级下册5.3 平行线的性质 同步培优(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 518.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 01:05:10 | ||
图片预览

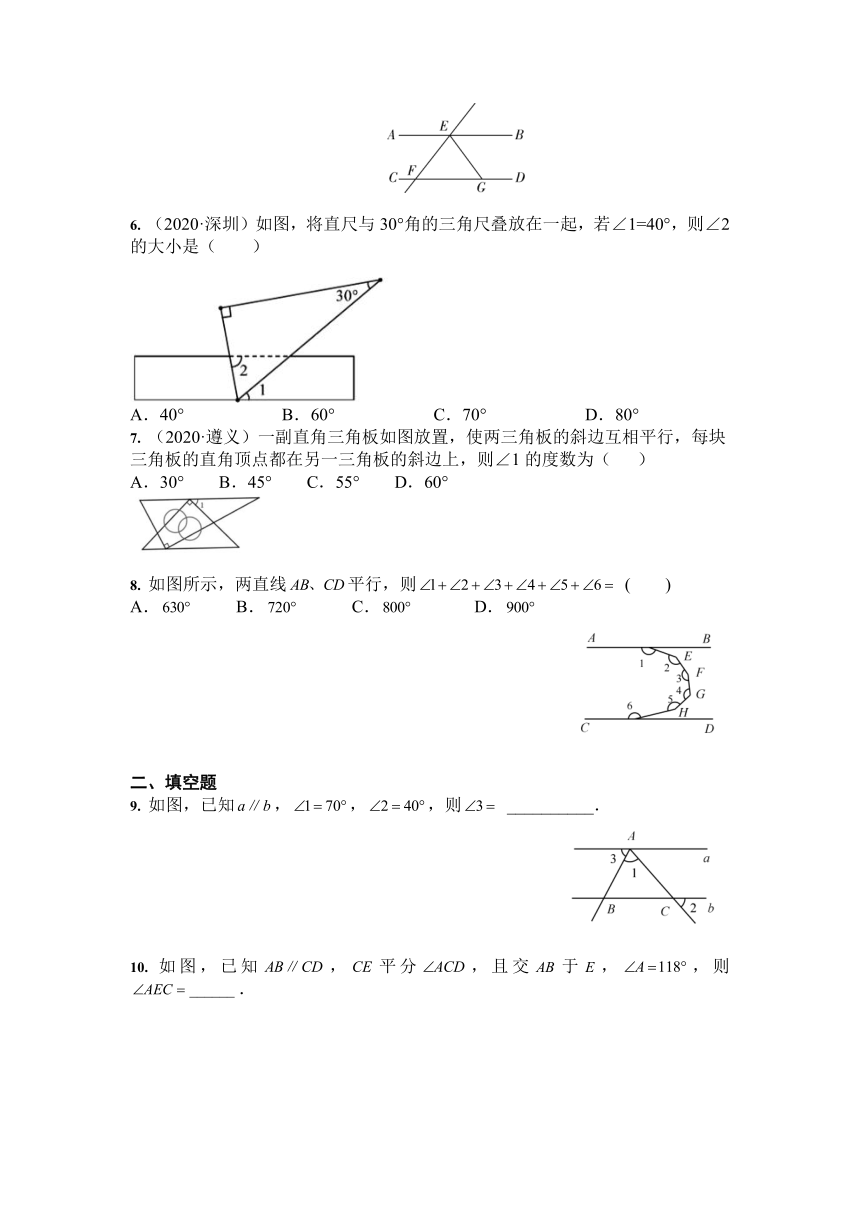
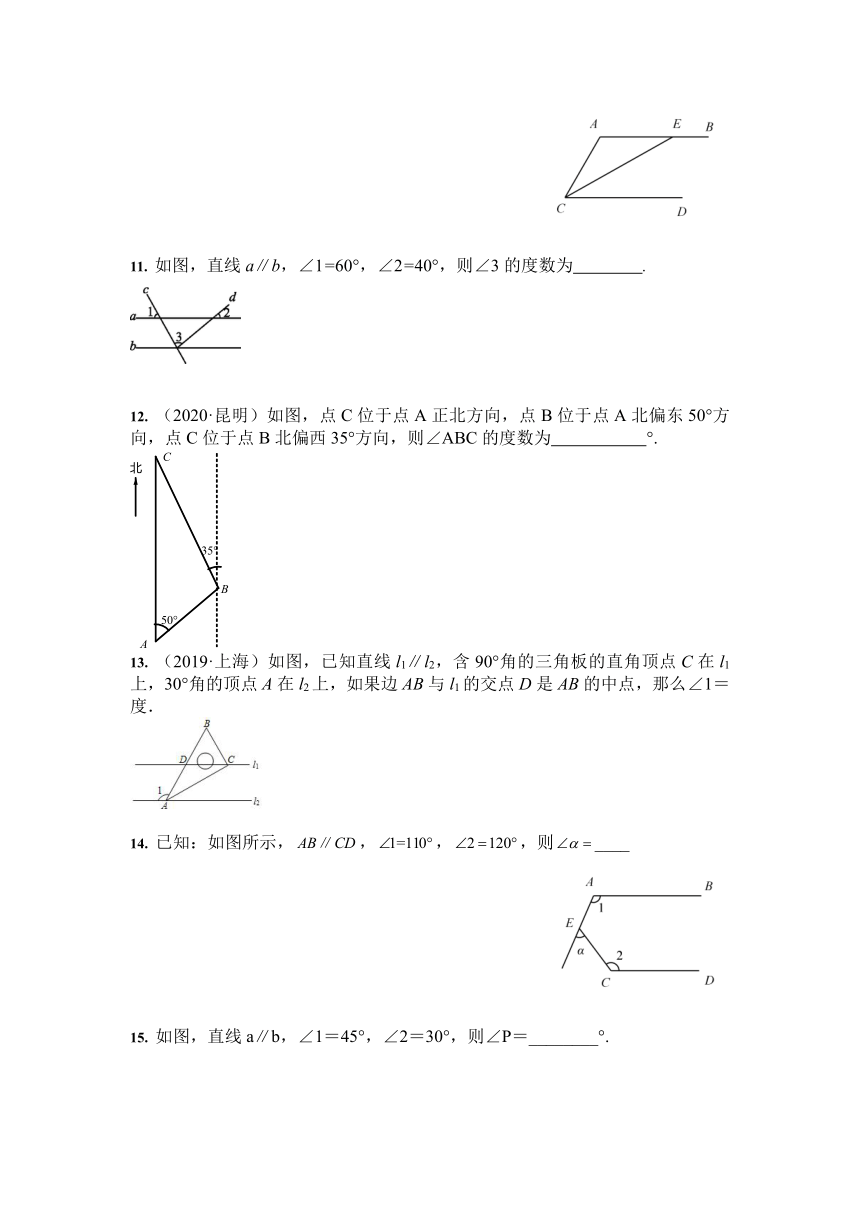
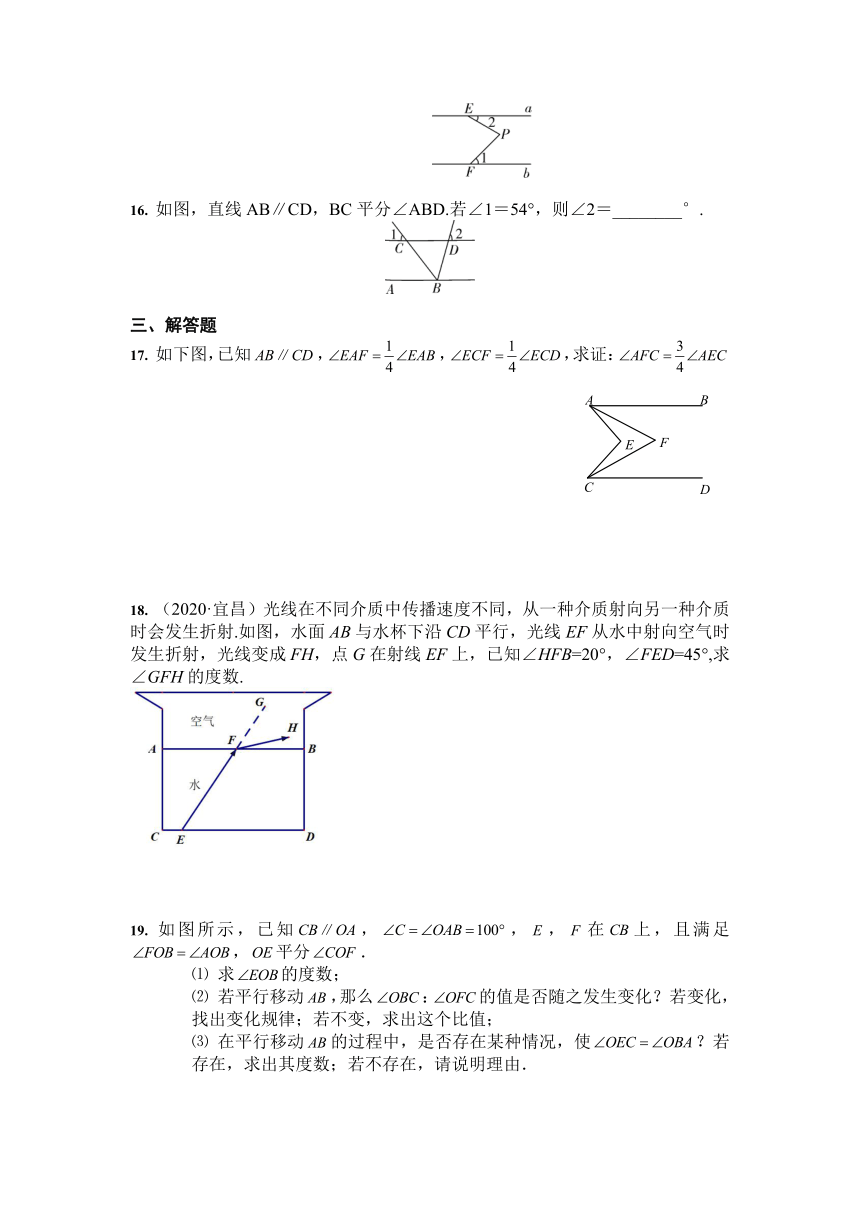
文档简介
人教版七年级数学下册:5.3 平行线的性质 同步培优
一、选择题
1. 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=110°,则∠2等于( )
A. 50° B. 70° C. 90° D. 110°
2. (2020·海南)如图,已知AB∥CD,直线AC和BD相交于点E,若∠ABE=70°,∠ACD=40°,则∠AEB等于( )
A.50° B.60° C.70° D.80°
3. (2020·内江)如图,已知直线,,则的度数为( )
A. B. C. D.
4. (2020·攀枝花)如图,平行线、被直线所截,过点作于点
,已知,则( )
A. B.
C. D.
5. 如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
A. 26° B. 64° C. 52° D.128°
6. (2020·深圳)如图,将直尺与30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
A.40° B.60° C.70° D.80°
7. (2020·遵义)一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A.30° B.45° C.55° D.60°
8. 如图所示,两直线平行,则 ( )
A. B. C. D.
二、填空题
9. 如图,已知,,,则 __________.
10. 如图,已知,平分,且交于,,则.
11. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3的度数为 .
12. (2020·昆明)如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
13. (2019·上海)如图,已知直线l1∥l2,含90°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上,如果边AB与l1的交点D是AB的中点,那么∠1= 度.
14. 已知:如图所示,,,,则____
15. 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=________°.
16. 如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.
三、解答题
17. 如下图,已知,,,求证:
18. (2020·宜昌)光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
19. 如图所示,已知,,,在上,且满足,平分.
⑴ 求的度数;
⑵ 若平行移动,那么:的值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值;
⑶ 在平行移动的过程中,是否存在某种情况,使?若存在,求出其度数;若不存在,请说明理由.
20. 如右图,在折线中,已知∠1=∠2=∠3=∠4=∠5,延长交于点.试探索与的关系,并说明理由.
人教版七年级数学下册:5.3 平行线的性质 同步培优-答案
一、选择题
1. 【答案】B 【解析】如解图,∵a∥b,∴∠3+∠4=180°,∵c∥d,∴∠2=∠4,∵∠1=∠3,∴∠2=180°-∠1=70°,故本题选B.
2. 【答案】C
【解析】∵AB∥CD,∴∠BAE=∠ACD=40°,∴∠AEB=180°-∠BAE-∠ABE=70°.
3. 【答案】 B
【解析】本题考查了平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.利用平行线的性质即可解决问题.
如图,
∵a∥b,∴∠1=∠3=50°,∴∠2=180° 50°=130°,因此本题选B.
4. 【答案】C
【解析】延长BG,交CD于H,∵∠1=50°,∴∠=50°,∵AB∥CD,∴∠B=∠BHD,∵BG⊥EF,∴∠FGH=90°,∴∠B=∠BHD=90°-∠2=90°-50°=40°.
5. 【答案】B 【解析】根据题意知∠EFG=52°,AB∥CD,∴∠BEF=180°-52°=128°,而EG平分∠BEF,∴∠BEG=∠BEF=64°,∴∠EGF=∠BEG=64°.
6. 【答案】D
【解析】根据直角三角形两锐角互余,求得∠3=90°-30°=60°;再由∠1=40°得到∠1+∠3=100°;最后根据平行线的性质,由AB∥CD,得到∠1+∠3+∠2=180°,求得∠2=80°,因此本题选D.
7. 【答案】B
【解析】本题考查平行线的性质.由两三角板的斜边互相平行,根据两直线平行内错角相等得∠1=45°,故选B.
8. 【答案】
【解析】分别过点做的平行线,再求各个角度的和.选D
二、填空题
9. 【答案】
10. 【答案】.
【解析】∵
∴
∴,
∵平分
∴
∵
∴
11. 【答案】80° [解析] 如图.
因为a∥b,
所以∠4=∠1=60°,
∠5=∠2=40°.
因为∠4+∠3+∠5=180°,
所以∠3=180°-∠4-∠5=180°-60°-40°=80°.
12. 【答案】95°
【解析】本题考查了方向角和平行线的性质.解答过程如下:如图所示,
∵AC∥BD,∴∠ABD=180°-∠A=180°-50°=130°.
又∵∠CBD=35°,∴∠ABC=∠ABD-∠CBD=130°-35°=95°.
13. 【答案】 120
【解析】∵D是斜边AB的中点,∴DA=DC,∴∠DCA=∠DAC=30°,∴∠2=∠DCA+∠DAC=60°,∵11∥l2,∴∠1+∠2=180°,∴∠1=180°-60°=120°.
14. 【答案】
【解析】如图所示,过点作的平行线,
则,
∵,
∴
∴
15. 【答案】75 【解析】如解图,过点P作PH∥a∥b,∴∠FPH=∠1,∠EPH=∠2,又∵∠1=45°,∠2=30°,∴∠EPF=∠EPH+∠HPF=30°+45°=75°.
16. 【答案】72 【解析】∵CD∥AB,∴∠CBA=∠1=54°,∠ABD+∠CDB=180°,∵CB平分∠ABD,∴∠DBC=∠CBA=54°,∴∠CDB=180°-54°-54°=72°,∴∠2=∠CDB=72°.
三、解答题
17. 【答案】
如右图所示,分别过点,做和的平行线,
易得:
即有:
18. 【答案】
解:AB//CD , GFB=∠FED=, ∠HFB=,∠GFH=∠GFB-∠HFB
【解析】要求∠GFH的角度,利用角度的和差关系可得.由图可得∠GFH=∠GFB-∠HFB,利用平行线的性质得∠GFB的角度,即可求出∠GFH的角度.
19. 【答案】
⑴ ;⑵ ;⑶ 存在,.
20. 【答案】
.理由:∵,
∴(内错角相等,两直线平行).
∵,
∴(内错角相等,两直线平行).
∴(平行于同一条直线的两直线平行).
∴(两直线平行,同位角相等).
又,
∴.
一、选择题
1. 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=110°,则∠2等于( )
A. 50° B. 70° C. 90° D. 110°
2. (2020·海南)如图,已知AB∥CD,直线AC和BD相交于点E,若∠ABE=70°,∠ACD=40°,则∠AEB等于( )
A.50° B.60° C.70° D.80°
3. (2020·内江)如图,已知直线,,则的度数为( )
A. B. C. D.
4. (2020·攀枝花)如图,平行线、被直线所截,过点作于点
,已知,则( )
A. B.
C. D.
5. 如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
A. 26° B. 64° C. 52° D.128°
6. (2020·深圳)如图,将直尺与30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
A.40° B.60° C.70° D.80°
7. (2020·遵义)一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A.30° B.45° C.55° D.60°
8. 如图所示,两直线平行,则 ( )
A. B. C. D.
二、填空题
9. 如图,已知,,,则 __________.
10. 如图,已知,平分,且交于,,则.
11. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3的度数为 .
12. (2020·昆明)如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为 °.
13. (2019·上海)如图,已知直线l1∥l2,含90°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上,如果边AB与l1的交点D是AB的中点,那么∠1= 度.
14. 已知:如图所示,,,,则____
15. 如图,直线a∥b,∠1=45°,∠2=30°,则∠P=________°.
16. 如图,直线AB∥CD,BC平分∠ABD.若∠1=54°,则∠2=________°.
三、解答题
17. 如下图,已知,,,求证:
18. (2020·宜昌)光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
19. 如图所示,已知,,,在上,且满足,平分.
⑴ 求的度数;
⑵ 若平行移动,那么:的值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值;
⑶ 在平行移动的过程中,是否存在某种情况,使?若存在,求出其度数;若不存在,请说明理由.
20. 如右图,在折线中,已知∠1=∠2=∠3=∠4=∠5,延长交于点.试探索与的关系,并说明理由.
人教版七年级数学下册:5.3 平行线的性质 同步培优-答案
一、选择题
1. 【答案】B 【解析】如解图,∵a∥b,∴∠3+∠4=180°,∵c∥d,∴∠2=∠4,∵∠1=∠3,∴∠2=180°-∠1=70°,故本题选B.
2. 【答案】C
【解析】∵AB∥CD,∴∠BAE=∠ACD=40°,∴∠AEB=180°-∠BAE-∠ABE=70°.
3. 【答案】 B
【解析】本题考查了平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.利用平行线的性质即可解决问题.
如图,
∵a∥b,∴∠1=∠3=50°,∴∠2=180° 50°=130°,因此本题选B.
4. 【答案】C
【解析】延长BG,交CD于H,∵∠1=50°,∴∠=50°,∵AB∥CD,∴∠B=∠BHD,∵BG⊥EF,∴∠FGH=90°,∴∠B=∠BHD=90°-∠2=90°-50°=40°.
5. 【答案】B 【解析】根据题意知∠EFG=52°,AB∥CD,∴∠BEF=180°-52°=128°,而EG平分∠BEF,∴∠BEG=∠BEF=64°,∴∠EGF=∠BEG=64°.
6. 【答案】D
【解析】根据直角三角形两锐角互余,求得∠3=90°-30°=60°;再由∠1=40°得到∠1+∠3=100°;最后根据平行线的性质,由AB∥CD,得到∠1+∠3+∠2=180°,求得∠2=80°,因此本题选D.
7. 【答案】B
【解析】本题考查平行线的性质.由两三角板的斜边互相平行,根据两直线平行内错角相等得∠1=45°,故选B.
8. 【答案】
【解析】分别过点做的平行线,再求各个角度的和.选D
二、填空题
9. 【答案】
10. 【答案】.
【解析】∵
∴
∴,
∵平分
∴
∵
∴
11. 【答案】80° [解析] 如图.
因为a∥b,
所以∠4=∠1=60°,
∠5=∠2=40°.
因为∠4+∠3+∠5=180°,
所以∠3=180°-∠4-∠5=180°-60°-40°=80°.
12. 【答案】95°
【解析】本题考查了方向角和平行线的性质.解答过程如下:如图所示,
∵AC∥BD,∴∠ABD=180°-∠A=180°-50°=130°.
又∵∠CBD=35°,∴∠ABC=∠ABD-∠CBD=130°-35°=95°.
13. 【答案】 120
【解析】∵D是斜边AB的中点,∴DA=DC,∴∠DCA=∠DAC=30°,∴∠2=∠DCA+∠DAC=60°,∵11∥l2,∴∠1+∠2=180°,∴∠1=180°-60°=120°.
14. 【答案】
【解析】如图所示,过点作的平行线,
则,
∵,
∴
∴
15. 【答案】75 【解析】如解图,过点P作PH∥a∥b,∴∠FPH=∠1,∠EPH=∠2,又∵∠1=45°,∠2=30°,∴∠EPF=∠EPH+∠HPF=30°+45°=75°.
16. 【答案】72 【解析】∵CD∥AB,∴∠CBA=∠1=54°,∠ABD+∠CDB=180°,∵CB平分∠ABD,∴∠DBC=∠CBA=54°,∴∠CDB=180°-54°-54°=72°,∴∠2=∠CDB=72°.
三、解答题
17. 【答案】
如右图所示,分别过点,做和的平行线,
易得:
即有:
18. 【答案】
解:AB//CD , GFB=∠FED=, ∠HFB=,∠GFH=∠GFB-∠HFB
【解析】要求∠GFH的角度,利用角度的和差关系可得.由图可得∠GFH=∠GFB-∠HFB,利用平行线的性质得∠GFB的角度,即可求出∠GFH的角度.
19. 【答案】
⑴ ;⑵ ;⑶ 存在,.
20. 【答案】
.理由:∵,
∴(内错角相等,两直线平行).
∵,
∴(内错角相等,两直线平行).
∴(平行于同一条直线的两直线平行).
∴(两直线平行,同位角相等).
又,
∴.
