2022年人教版八年级数学下册19.2 一次函数 同步培优(Word版含答案)
文档属性
| 名称 | 2022年人教版八年级数学下册19.2 一次函数 同步培优(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 564.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 01:09:16 | ||
图片预览


文档简介
人教版 八年级数学下册:19.2 一次函数 同步培优
一、选择题
1. 已知正比例函数 (,为常数),经过点(2,4),以下哪个点不在该正比例函数图图象上( )
A.(-2,-4) B.(0,0) C.(1,2) D.
2. 如图,一次函数的图象大致是( )
A B C D
3. 已知函数图象如图所示,则此函数的解析式为( )
A.
B.
C.
D.
4. 如果的自变量增加4,函数值相应地减少16,则的值为( )
A.4 B.- 4 C. D.
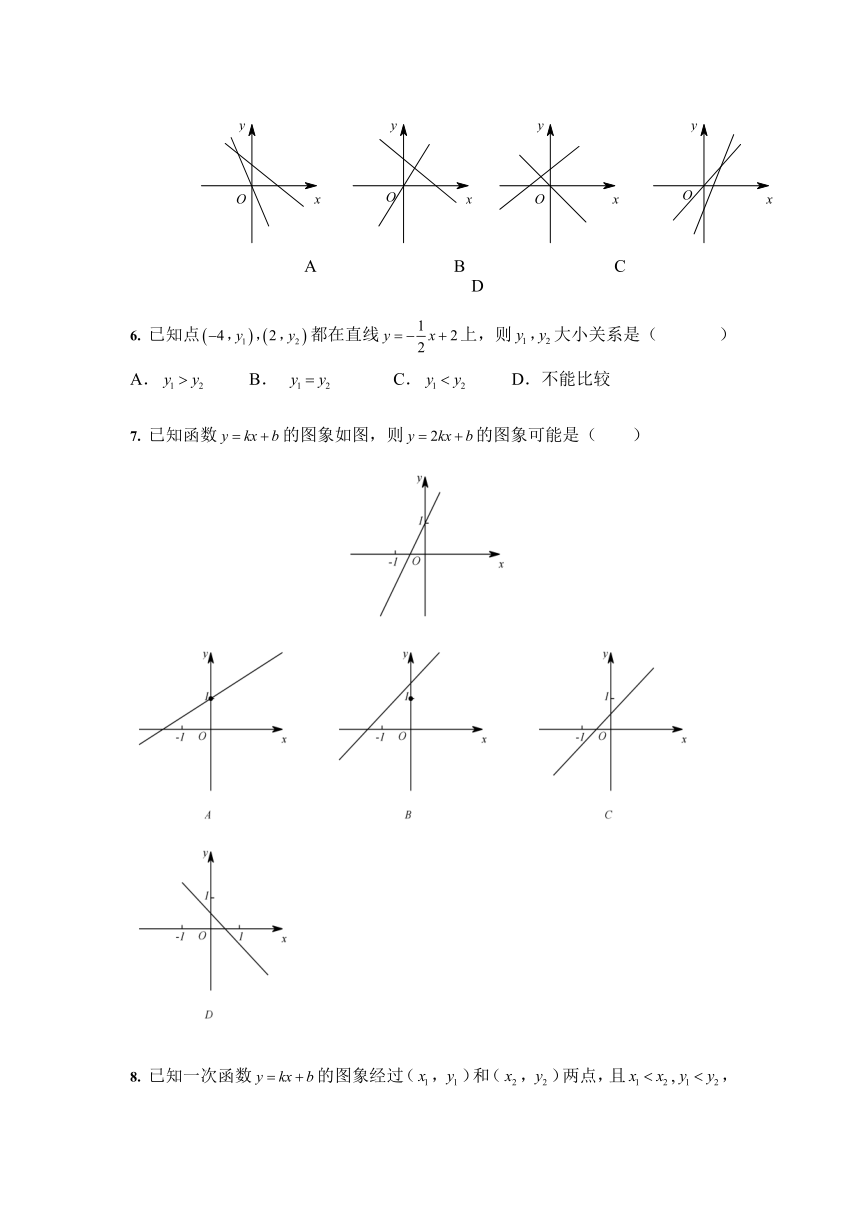
5. 下列图形中,表示一次函数与正比例函数(、为常数且)的图像是下图中的( )
A B C D
6. 已知点都在直线上,则大小关系是( )
A. B. C. D.不能比较
7. 已知函数的图象如图,则的图象可能是( )
8. 已知一次函数的图象经过(,)和(,)两点,且,,则( )
A. B., C., D.
9. 若,为一次函数,的图象上的两个不同点,且,设,,则( )
A. B. C. D. 以上都不对
二、填空题
10. 若一次函数的图象不经过第一象限,则的取值范围是 .
11. 将直线向右平移2个单位所得的直线的解析式是 .
12. 若一次函数的图像不过第一象限,则的取值范围是___________.
13. 如图所示,在同一直角坐标系中,一次函数,,,的图像分别是,,,;那么,,,的大小关系是 .
14. 一个一次函数的图象与直线平行,与轴,轴分别交于,两点,并且通过,则在线段上(包括端点,两点),横纵坐标都是整数的点有_______个.
15. 已知,并且,则直线一定通过 象限.
三、解答题
16. 已知,当取何值时,是的正比例函数?
17. 已知是一次函数,求它的解析式.
18. 把函数的图像向右平行移动个单位,求:
⑴ 平移后得到的直线解析式;
⑵ 平移后的直线到两坐标轴距离相等的点的坐标.
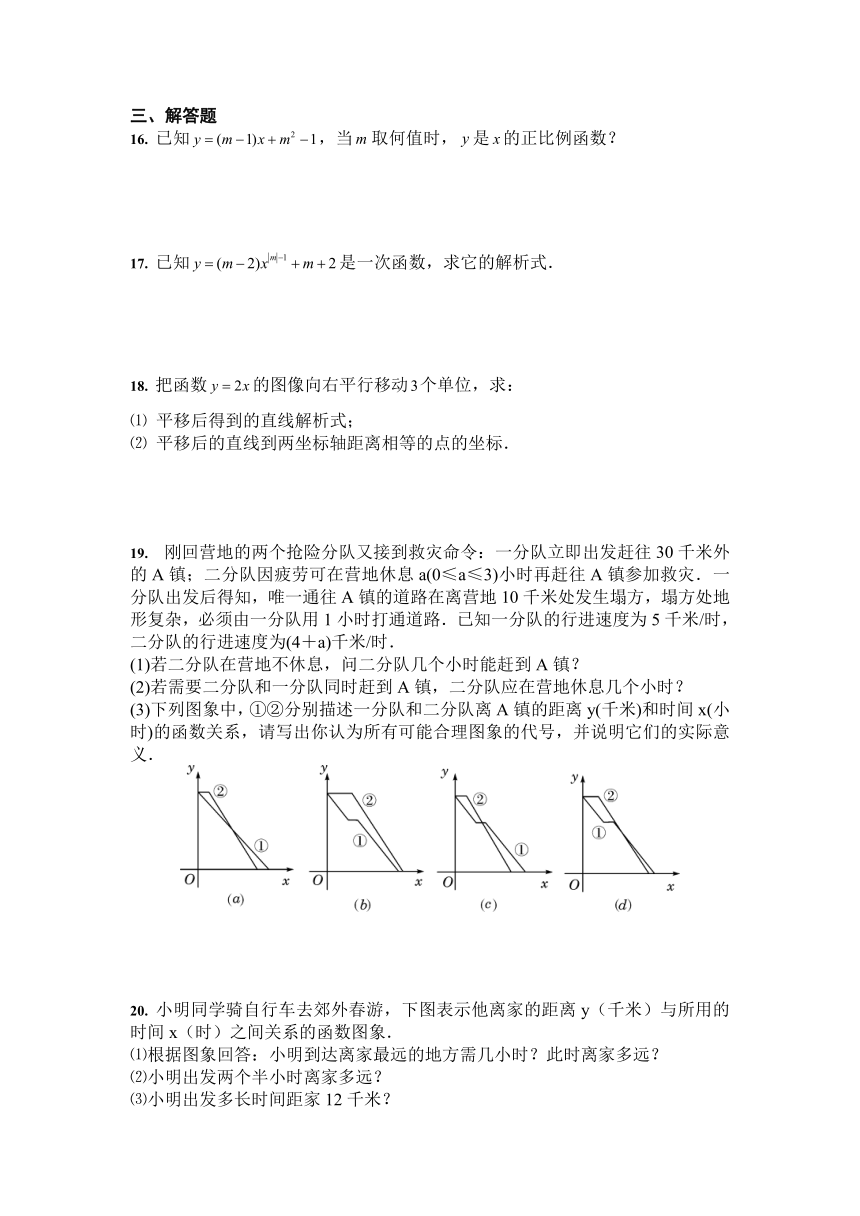
19. 刚回营地的两个抢险分队又接到救灾命令:一分队立即出发赶往30千米外的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再赶往A镇参加救灾.一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方处地形复杂,必须由一分队用1小时打通道路.已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.
(1)若二分队在营地不休息,问二分队几个小时能赶到A镇?
(2)若需要二分队和一分队同时赶到A镇,二分队应在营地休息几个小时?
(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理图象的代号,并说明它们的实际意义.
20. 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.
⑴根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
⑵小明出发两个半小时离家多远?
⑶小明出发多长时间距家12千米?
人教版 八年级数学下册:19.2 一次函数 同步培优-答案
一、选择题
1. 【答案】D
2. 【答案】B
3. 【答案】B
【解析】由题意,正比例函数经过点(-1,2),求出函数解析式为,同时根据图象看出自变量的取值范围为
4. 【答案】B
【解析】由题意得:,将带入等式,即,所以解出
5. 【答案】A
【解析】解此类图像题时,采用假设法,即假设其中一条直线的位置是正确的,据此推出参数的符号,
然后根据参数的符号来判断另一条直线的位置是否正确.
6. 【答案】A
【解析】考察一次函数的性质,的,则随的增大而减小
7. 【答案】C
【解析】由的图象,,与轴交点为,因为与相交于轴上的同一点,所以b值相同,与轴交点坐标为
8. 【答案】A
9. 【答案】C
【解析】,,
所以
二、填空题
10. 【答案】
【解析】由题意,解不等式组得出的取值范围.
11. 【答案】
12. 【答案】
【解析】由题意可得:,解得
13. 【答案】
【解析】.我们探究可以发现:越大,越接近于轴;越小,越接近于轴.在各个象限的增大境况如图所示.
14. 【答案】5
【解析】依题意可求出这个一次函数的解析式为:,于是可求得,.
∴的取值范围为的整数,的取值范围为:的整数.
∴求线段上的整点坐标可转化为方程在上述条件下的整数解.
∴当时,;当时,;当时,;当时,;当时,,故可知线段上有5个整点.
15. 【答案】二、三
【解析】由已知得:①,②,③
①+②+③,得:
时,,这时,,直线经过一、二、三象限;
当时,,这时,直线经过二、三、四象限.
故可知直线一定通过二、三象限.
三、解答题
16. 【答案】
-1
【解析】∵正比例函数,所以
∴且
∴当时,是的正比例函数.
17. 【答案】
【解析】根据题意可得:,解得,所求一次函数为.
18. 【答案】
⑴;⑵或
【解析】⑴因为直线向右平移个单位,所以,且平移后经过点.设所求解析式为,
将代入,得.所以所求直线解析式为.
⑵因为到两坐标轴距离相等的点在直线或上,所以解方程组
和
得和
19. 【答案】
解:(1)若二分队在营地不休息,则a=0,速度为4千米/时,行至塌方处需=2.5(小时),因为一分队到塌方处并打通道路需要+1=3(小时),故二分队在塌方处需要停留0.5小时,所以二分队在营地不休息赶到A镇需2.5+0.5+=8(小时).
(2)一分队赶到A镇共需+1=7(小时).
(ⅰ)若二分队在塌方处需停留,则后20千米需与一分队同行,故4+a=5,即a=1,这与二分队在塌方处停留矛盾,舍去;
(ⅱ)若二分队在塌方处不停留,则(4+a)(7-a)=30,即a2-3a+2=0,解得a1=1,a2=2.
经检验a1=1,a2=2均符合题意.
答:二分队应在营地休息1小时或2小时.(其他解法只要合理即给分)
(3)合理的图象为(b)、(d).
图象(b)表明二分队在营地休息时间恰当(2<a≤3),后于一分队赶到A镇;
图象(d)表明二分队在营地休息时间恰当(1<a<2),先于一分队赶到A镇.
20. 【答案】
⑴3小时,30千米;⑵千米;⑶48分或5小时12分
【解析】⑴由图象可知小明到达离家最远的地方需3小时,此时,他离家30千米.
⑵∵小明出发2小时时,离家15千米.由于在CD段小明走的路程为15千米,时间为1小时,故小明这一段的速度为15千米/时.
∴(千米)
∴(千米)
∴小明出发两个半小时离家千米.
⑶由图象可以看出小明从出发到距离家12千米有两个时刻,一是在AB段,二是在EF段,故分两种情况:
①∵小明出发到1小时时,匀速前行,其速度为15千米/时
∴(时),小时48分
②∵小明出发4小时后返回,
∴返回时速度为(千米/时)
∴(时)
时1小时12分
∴4小时+1小时12分5小时12分
故小明出发48分和出发5小时12分时离家都为12千米.
一、选择题
1. 已知正比例函数 (,为常数),经过点(2,4),以下哪个点不在该正比例函数图图象上( )
A.(-2,-4) B.(0,0) C.(1,2) D.
2. 如图,一次函数的图象大致是( )
A B C D
3. 已知函数图象如图所示,则此函数的解析式为( )
A.
B.
C.
D.
4. 如果的自变量增加4,函数值相应地减少16,则的值为( )
A.4 B.- 4 C. D.
5. 下列图形中,表示一次函数与正比例函数(、为常数且)的图像是下图中的( )
A B C D
6. 已知点都在直线上,则大小关系是( )
A. B. C. D.不能比较
7. 已知函数的图象如图,则的图象可能是( )
8. 已知一次函数的图象经过(,)和(,)两点,且,,则( )
A. B., C., D.
9. 若,为一次函数,的图象上的两个不同点,且,设,,则( )
A. B. C. D. 以上都不对
二、填空题
10. 若一次函数的图象不经过第一象限,则的取值范围是 .
11. 将直线向右平移2个单位所得的直线的解析式是 .
12. 若一次函数的图像不过第一象限,则的取值范围是___________.
13. 如图所示,在同一直角坐标系中,一次函数,,,的图像分别是,,,;那么,,,的大小关系是 .
14. 一个一次函数的图象与直线平行,与轴,轴分别交于,两点,并且通过,则在线段上(包括端点,两点),横纵坐标都是整数的点有_______个.
15. 已知,并且,则直线一定通过 象限.
三、解答题
16. 已知,当取何值时,是的正比例函数?
17. 已知是一次函数,求它的解析式.
18. 把函数的图像向右平行移动个单位,求:
⑴ 平移后得到的直线解析式;
⑵ 平移后的直线到两坐标轴距离相等的点的坐标.
19. 刚回营地的两个抢险分队又接到救灾命令:一分队立即出发赶往30千米外的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再赶往A镇参加救灾.一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方处地形复杂,必须由一分队用1小时打通道路.已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时.
(1)若二分队在营地不休息,问二分队几个小时能赶到A镇?
(2)若需要二分队和一分队同时赶到A镇,二分队应在营地休息几个小时?
(3)下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理图象的代号,并说明它们的实际意义.
20. 小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的函数图象.
⑴根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
⑵小明出发两个半小时离家多远?
⑶小明出发多长时间距家12千米?
人教版 八年级数学下册:19.2 一次函数 同步培优-答案
一、选择题
1. 【答案】D
2. 【答案】B
3. 【答案】B
【解析】由题意,正比例函数经过点(-1,2),求出函数解析式为,同时根据图象看出自变量的取值范围为
4. 【答案】B
【解析】由题意得:,将带入等式,即,所以解出
5. 【答案】A
【解析】解此类图像题时,采用假设法,即假设其中一条直线的位置是正确的,据此推出参数的符号,
然后根据参数的符号来判断另一条直线的位置是否正确.
6. 【答案】A
【解析】考察一次函数的性质,的,则随的增大而减小
7. 【答案】C
【解析】由的图象,,与轴交点为,因为与相交于轴上的同一点,所以b值相同,与轴交点坐标为
8. 【答案】A
9. 【答案】C
【解析】,,
所以
二、填空题
10. 【答案】
【解析】由题意,解不等式组得出的取值范围.
11. 【答案】
12. 【答案】
【解析】由题意可得:,解得
13. 【答案】
【解析】.我们探究可以发现:越大,越接近于轴;越小,越接近于轴.在各个象限的增大境况如图所示.
14. 【答案】5
【解析】依题意可求出这个一次函数的解析式为:,于是可求得,.
∴的取值范围为的整数,的取值范围为:的整数.
∴求线段上的整点坐标可转化为方程在上述条件下的整数解.
∴当时,;当时,;当时,;当时,;当时,,故可知线段上有5个整点.
15. 【答案】二、三
【解析】由已知得:①,②,③
①+②+③,得:
时,,这时,,直线经过一、二、三象限;
当时,,这时,直线经过二、三、四象限.
故可知直线一定通过二、三象限.
三、解答题
16. 【答案】
-1
【解析】∵正比例函数,所以
∴且
∴当时,是的正比例函数.
17. 【答案】
【解析】根据题意可得:,解得,所求一次函数为.
18. 【答案】
⑴;⑵或
【解析】⑴因为直线向右平移个单位,所以,且平移后经过点.设所求解析式为,
将代入,得.所以所求直线解析式为.
⑵因为到两坐标轴距离相等的点在直线或上,所以解方程组
和
得和
19. 【答案】
解:(1)若二分队在营地不休息,则a=0,速度为4千米/时,行至塌方处需=2.5(小时),因为一分队到塌方处并打通道路需要+1=3(小时),故二分队在塌方处需要停留0.5小时,所以二分队在营地不休息赶到A镇需2.5+0.5+=8(小时).
(2)一分队赶到A镇共需+1=7(小时).
(ⅰ)若二分队在塌方处需停留,则后20千米需与一分队同行,故4+a=5,即a=1,这与二分队在塌方处停留矛盾,舍去;
(ⅱ)若二分队在塌方处不停留,则(4+a)(7-a)=30,即a2-3a+2=0,解得a1=1,a2=2.
经检验a1=1,a2=2均符合题意.
答:二分队应在营地休息1小时或2小时.(其他解法只要合理即给分)
(3)合理的图象为(b)、(d).
图象(b)表明二分队在营地休息时间恰当(2<a≤3),后于一分队赶到A镇;
图象(d)表明二分队在营地休息时间恰当(1<a<2),先于一分队赶到A镇.
20. 【答案】
⑴3小时,30千米;⑵千米;⑶48分或5小时12分
【解析】⑴由图象可知小明到达离家最远的地方需3小时,此时,他离家30千米.
⑵∵小明出发2小时时,离家15千米.由于在CD段小明走的路程为15千米,时间为1小时,故小明这一段的速度为15千米/时.
∴(千米)
∴(千米)
∴小明出发两个半小时离家千米.
⑶由图象可以看出小明从出发到距离家12千米有两个时刻,一是在AB段,二是在EF段,故分两种情况:
①∵小明出发到1小时时,匀速前行,其速度为15千米/时
∴(时),小时48分
②∵小明出发4小时后返回,
∴返回时速度为(千米/时)
∴(时)
时1小时12分
∴4小时+1小时12分5小时12分
故小明出发48分和出发5小时12分时离家都为12千米.
