三角形的外角
图片预览


文档简介
课件23张PPT。三角形的内角 三角形内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
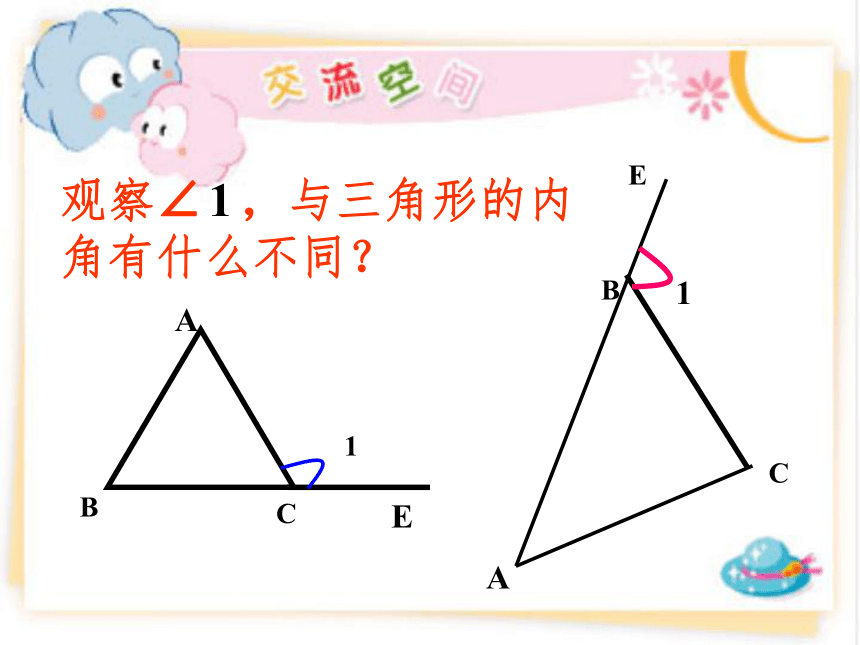
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. ABCEABC1E1观察∠ ,与三角形的内角有什么不同?1 三角形的一边与另一边的
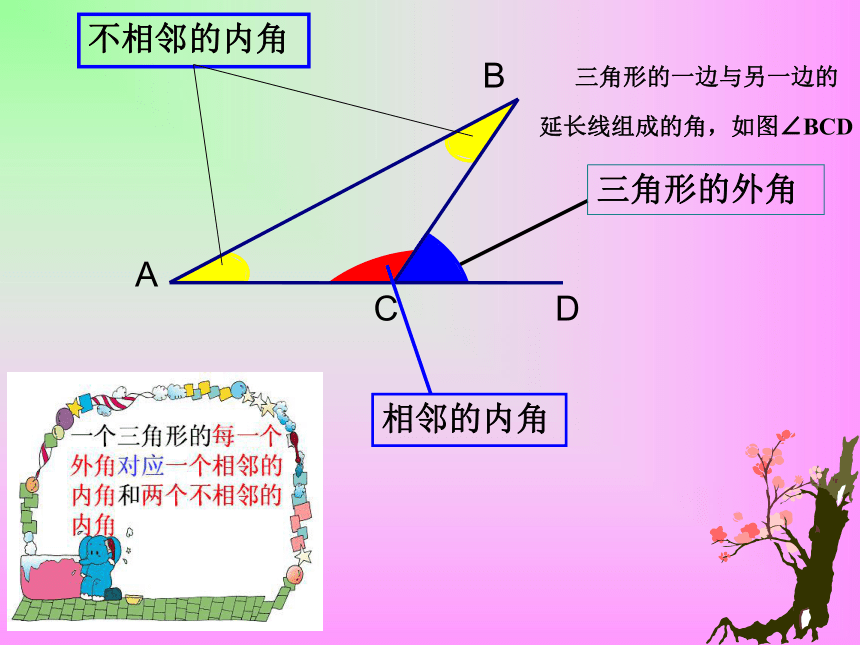
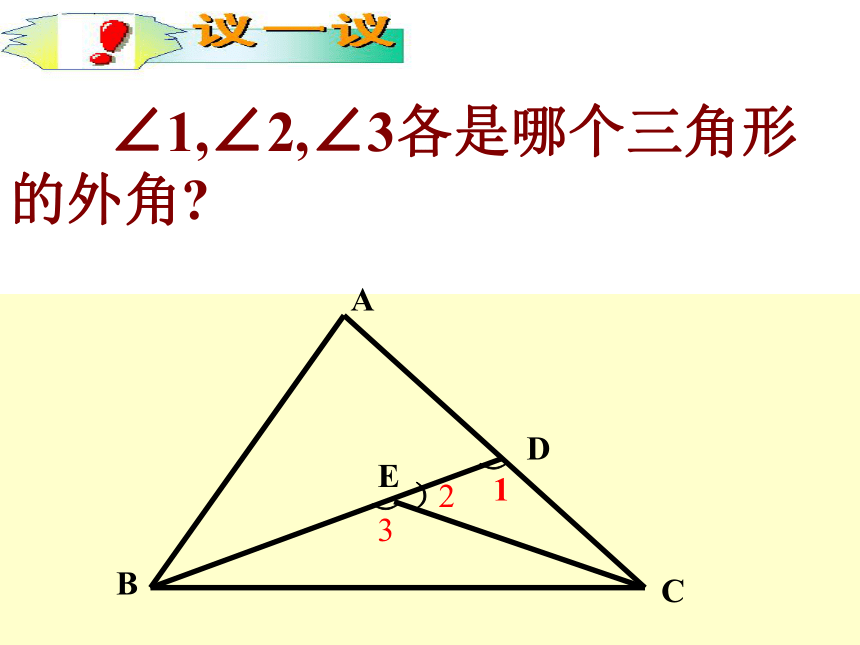
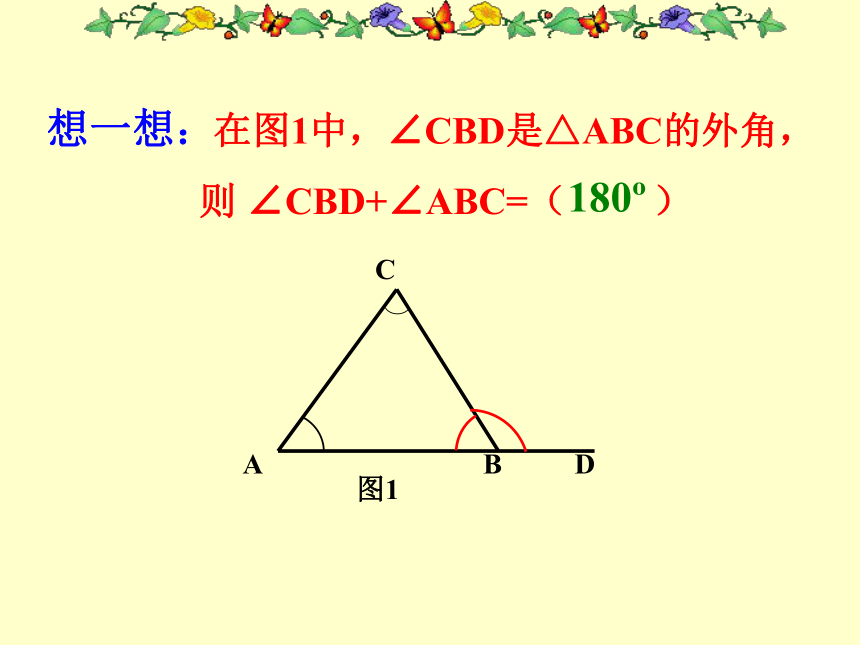
延长线组成的角,如图∠BCD ∠1,∠2,∠3各是哪个三角形的外角?ABCDE12︶︶)3想一想:在图1中,∠CBD是△ABC的外角,
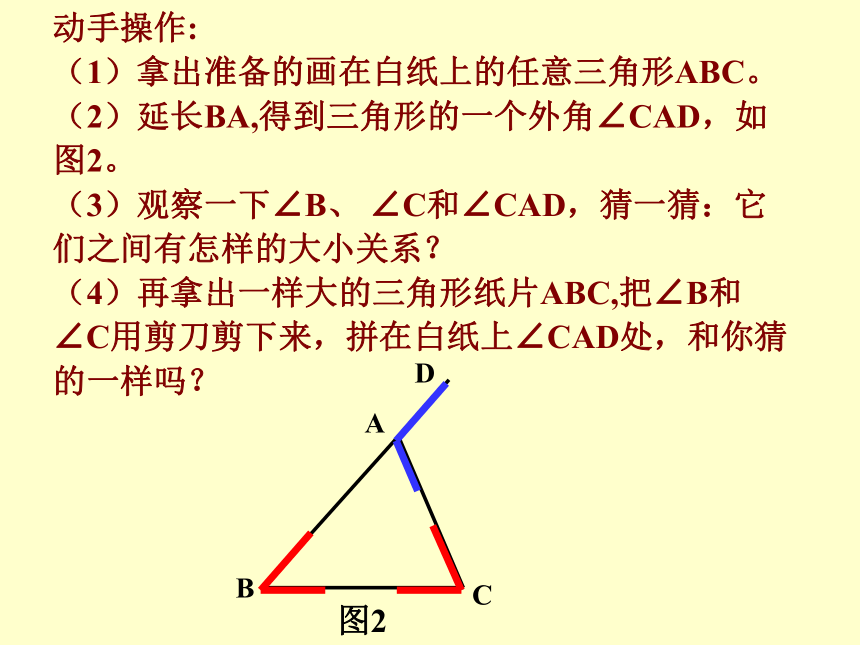
则 ∠CBD+∠ABC=( )180o动手操作:
(1)拿出准备的画在白纸上的任意三角形ABC。
(2)延长BA,得到三角形的一个外角∠CAD,如图2。
(3)观察一下∠B、 ∠C和∠CAD,猜一猜:它们之间有怎样的大小关系?
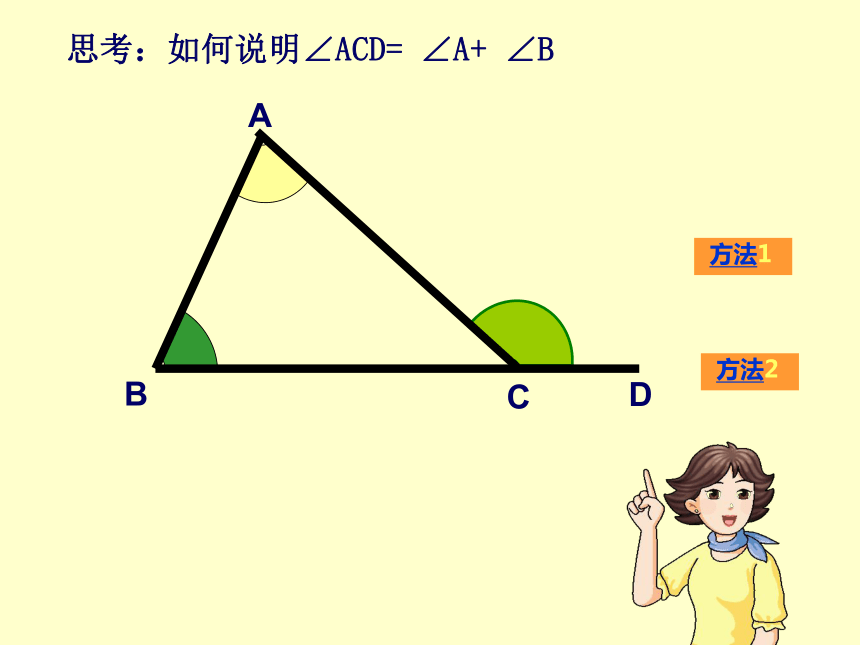
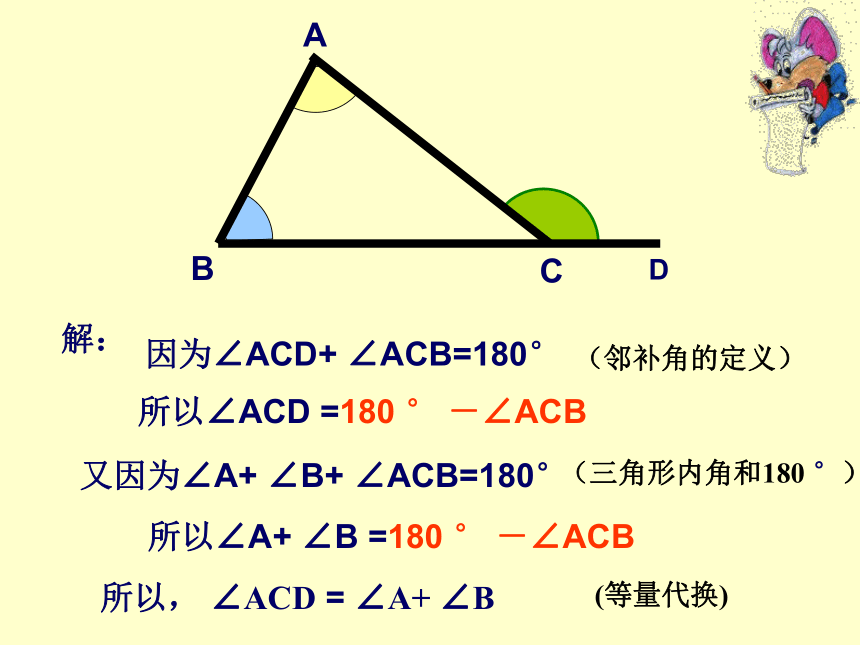
(4)再拿出一样大的三角形纸片ABC,把∠B和 ∠C用剪刀剪下来,拼在白纸上∠CAD处,和你猜的一样吗?图2思考:如何说明∠ACD= ∠A+ ∠BDD因为∠ACD+ ∠ACB=180°又因为∠A+ ∠B+ ∠ACB=180°所以, ∠ACD = ∠A+ ∠B解:所以∠ACD =180 ° -∠ACB所以∠A+ ∠B =180 ° -∠ACB(邻补角的定义)(三角形内角和180 °)(等量代换)(CE//BA)AE说一说小明用另一种画平行线的方法解释了外角的这个性质,你知道他是怎么解释的吗?CBDD解:过点C作CE平行于ABABC所以 ∠1= ∠B
(两直线平行,同位角相等) ∠2= ∠A
(两直线平行,内错角相等)所以 ∠ACD= ∠1+ ∠2= ∠A+ ∠B结论:三角形的一个外角等于与它不相邻的两个内角的和。 ∠ACD ∠A (<、>);∠ACD ∠B (<、>)结论:三角形的一个外角大于与它不相邻的任何一个内角。D>>选谁 ?∠ACD= ∠A+ ∠B90o85o95o60o43o30o求下列各图中∠α的度数。试一试议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°所以 ∠1+ ∠2+ ∠3=360° 国旗上的数学问题 如图:求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。FG12FG解:因为 ∠1是△FBE的外角 所以 ∠1=∠B+ ∠E 同理 ∠2=∠A+∠D在△CFG中
∠C+∠1+∠2=180o所以 ∠A+ ∠ B+∠C+ ∠ D+∠E= 180o课堂小结:今天你学会了什么?三角形的外角的性质:(3)三角形的一个外角大于与它不相邻的任何一个内角。(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
如图,计算∠BOC的度数。思维拓展:如图,计算∠BOC的度数。思维拓展:E谢谢大家Byebye
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. ABCEABC1E1观察∠ ,与三角形的内角有什么不同?1 三角形的一边与另一边的
延长线组成的角,如图∠BCD ∠1,∠2,∠3各是哪个三角形的外角?ABCDE12︶︶)3想一想:在图1中,∠CBD是△ABC的外角,
则 ∠CBD+∠ABC=( )180o动手操作:
(1)拿出准备的画在白纸上的任意三角形ABC。
(2)延长BA,得到三角形的一个外角∠CAD,如图2。
(3)观察一下∠B、 ∠C和∠CAD,猜一猜:它们之间有怎样的大小关系?
(4)再拿出一样大的三角形纸片ABC,把∠B和 ∠C用剪刀剪下来,拼在白纸上∠CAD处,和你猜的一样吗?图2思考:如何说明∠ACD= ∠A+ ∠BDD因为∠ACD+ ∠ACB=180°又因为∠A+ ∠B+ ∠ACB=180°所以, ∠ACD = ∠A+ ∠B解:所以∠ACD =180 ° -∠ACB所以∠A+ ∠B =180 ° -∠ACB(邻补角的定义)(三角形内角和180 °)(等量代换)(CE//BA)AE说一说小明用另一种画平行线的方法解释了外角的这个性质,你知道他是怎么解释的吗?CBDD解:过点C作CE平行于ABABC所以 ∠1= ∠B
(两直线平行,同位角相等) ∠2= ∠A
(两直线平行,内错角相等)所以 ∠ACD= ∠1+ ∠2= ∠A+ ∠B结论:三角形的一个外角等于与它不相邻的两个内角的和。 ∠ACD ∠A (<、>);∠ACD ∠B (<、>)结论:三角形的一个外角大于与它不相邻的任何一个内角。D>>选谁 ?∠ACD= ∠A+ ∠B90o85o95o60o43o30o求下列各图中∠α的度数。试一试议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°所以 ∠1+ ∠2+ ∠3=360° 国旗上的数学问题 如图:求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。FG12FG解:因为 ∠1是△FBE的外角 所以 ∠1=∠B+ ∠E 同理 ∠2=∠A+∠D在△CFG中
∠C+∠1+∠2=180o所以 ∠A+ ∠ B+∠C+ ∠ D+∠E= 180o课堂小结:今天你学会了什么?三角形的外角的性质:(3)三角形的一个外角大于与它不相邻的任何一个内角。(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
如图,计算∠BOC的度数。思维拓展:如图,计算∠BOC的度数。思维拓展:E谢谢大家Byebye
