沪科版八年级上 15.2 三角形全等的判定SAS(课件)
文档属性
| 名称 | 沪科版八年级上 15.2 三角形全等的判定SAS(课件) |  | |
| 格式 | zip | ||
| 文件大小 | 627.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-24 20:40:32 | ||
图片预览




文档简介
课件35张PPT。15.2三角形全等的判定(一)
边角边ABCA'B'
C'
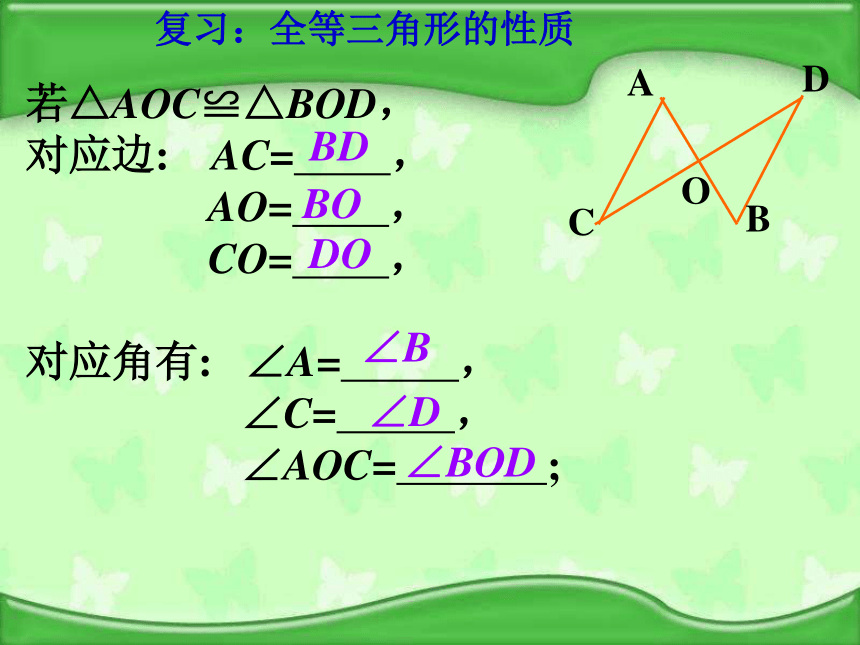
若△AOC≌△BOD,
对应边: AC= ,
AO= ,
CO= ,
对应角有: ∠A= ,
∠C= ,
∠AOC= ;
复习:全等三角形的性质BDBODO∠B∠D∠BOD操作第一组:一条边为6cm;
第二组:一个角是45°;
第三组:两条边分别为4cm和6cm;
第四组:一条边为6cm,一个角为45°;
第五组:两个角分别为45°和60°.
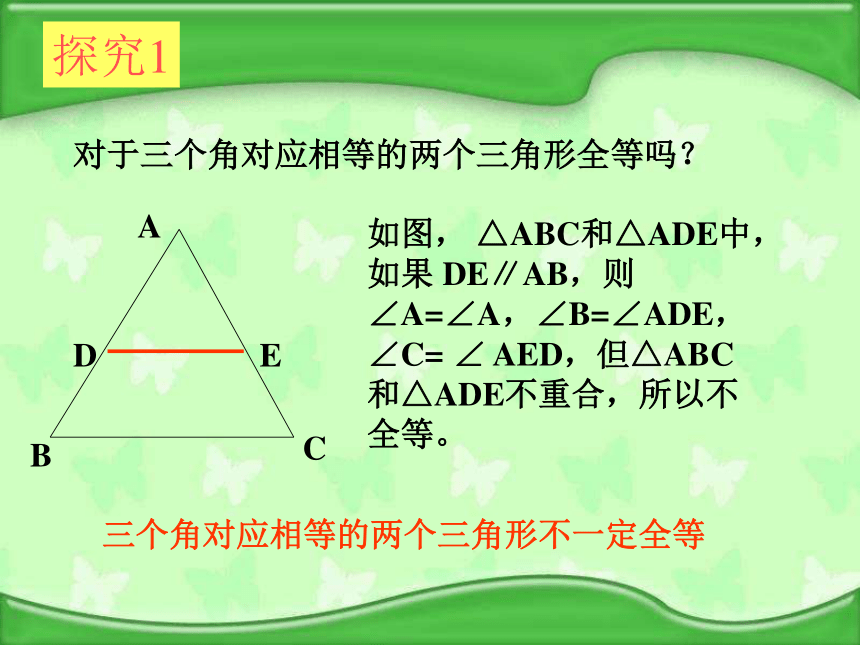
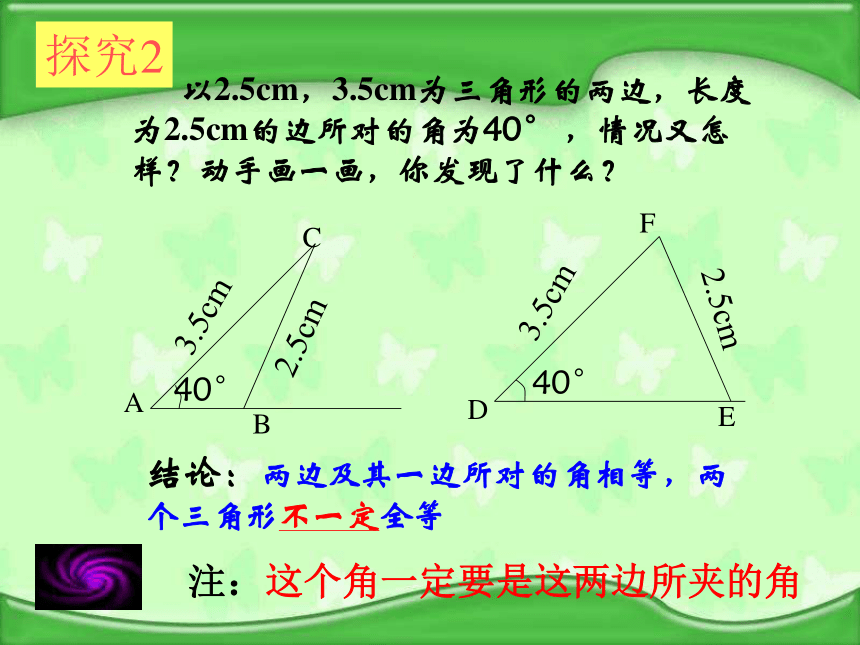
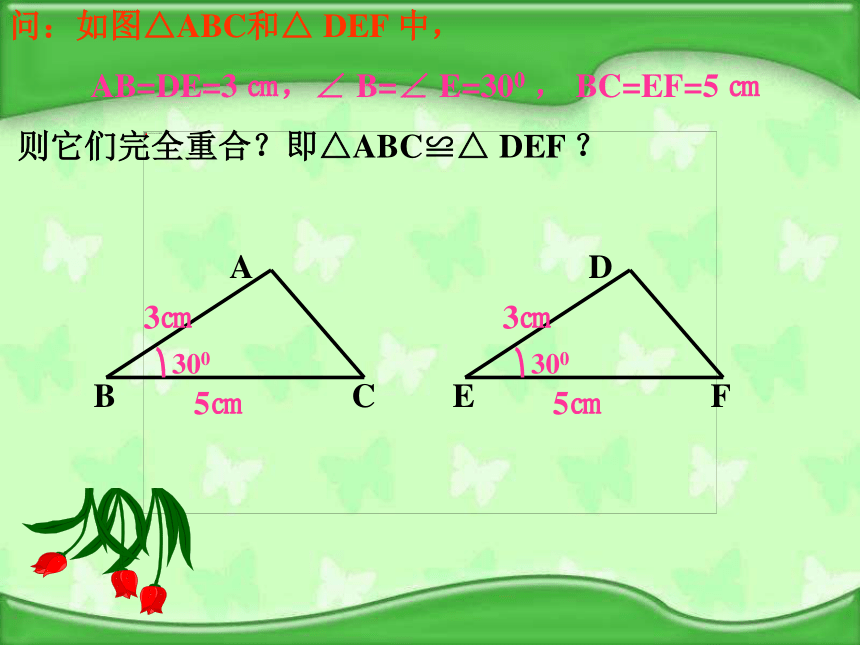
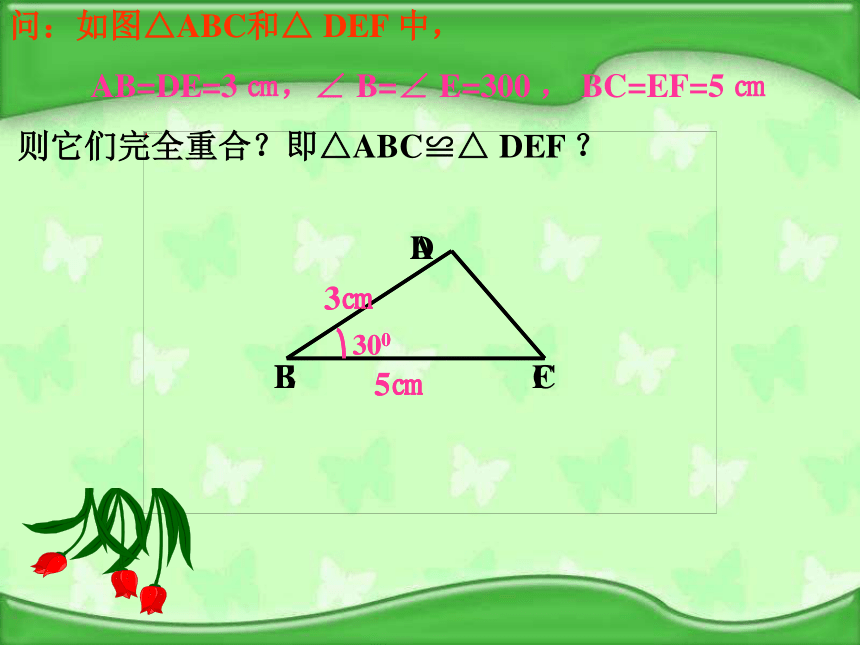
按下列条件做三角形,并通过比较判断它们之间是否全等,由此你有什么发现?大家要合作哦探究1对于三个角对应相等的两个三角形全等吗?如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。三个角对应相等的两个三角形不一定全等 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2注:这个角一定要是这两边所夹的角做一做:画△ABC,使AB=3cm,AC=4cm。画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?探究3先任意画出一个△ABC,再画出一个△A′B′C′使A′B′=AB,A′C′=AC,∠A=∠A′。画法:2. 在射线A′D上截取A′B′= AB3. 在射线A′E上截取A′C′=AC1. 画∠DA′E= ∠A4.连接B′C′∴△A′B′C′就是所求的三角形把你们所画的三角形剪下来与原来的三角形进行比较,它们能互相重合吗?探究4问:如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则它们完全重合?即△ABC≌△ DEF ?问:如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
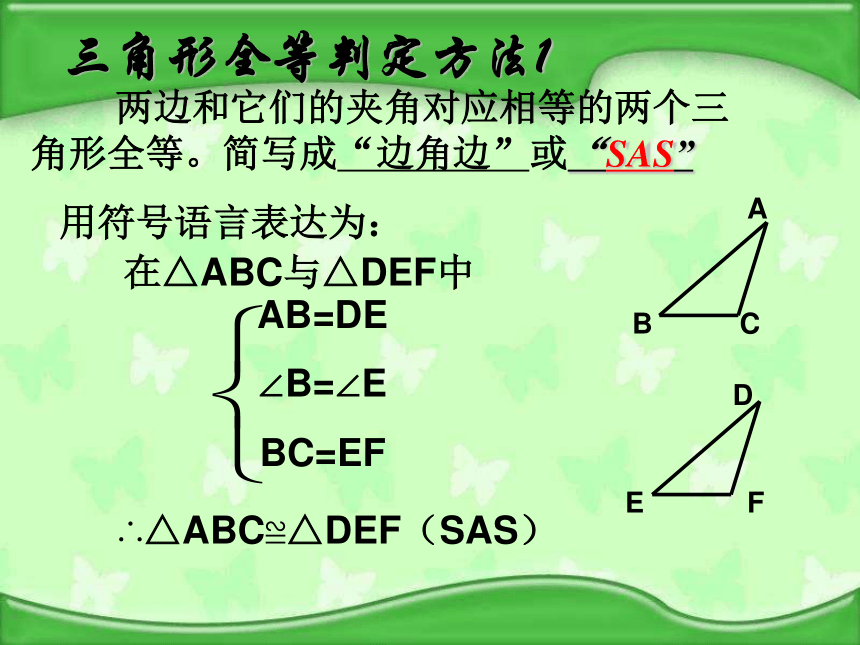
则它们完全重合?即△ABC≌△ DEF ? 三角形全等判定方法1用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
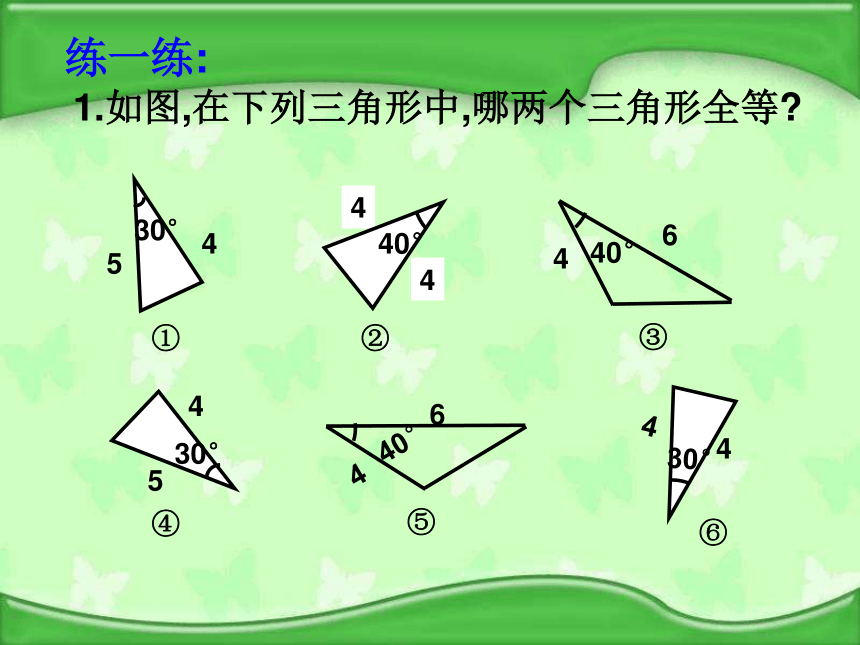
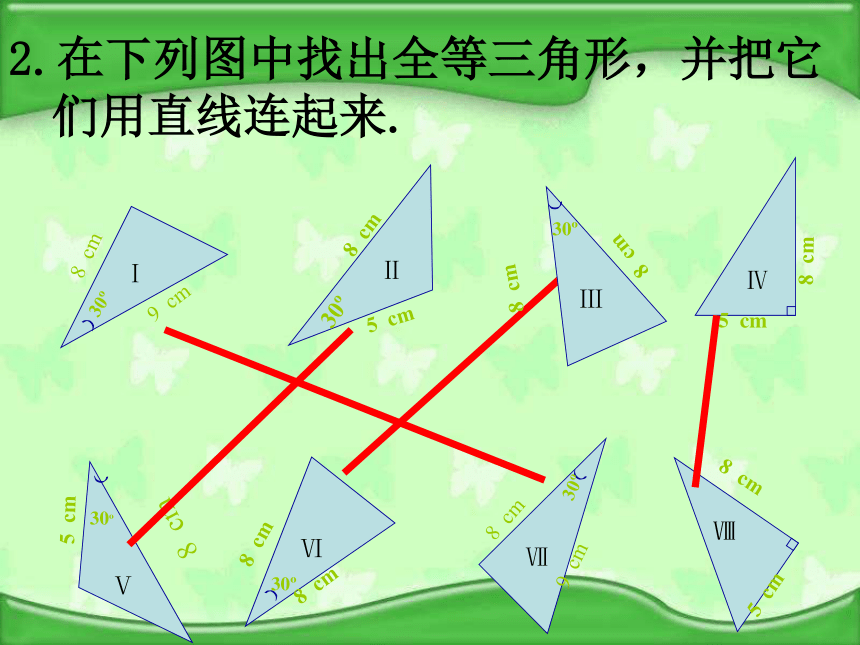
44练一练:1.如图,在下列三角形中,哪两个三角形全等?445530°30°4430°4640°4640°40°①③②⑥⑤④2.在下列图中找出全等三角形,并把它们用直线连起来.已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA分析:观察图形,结合已知条件,知,AD=CB,AC=CA,但没有给出两组对应边的夹角(∠1,∠2)相等。所以,应设法先证明∠1=∠2,才能使全等条件充足。AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)例1:证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中DC1AB2B范例学习动 态 演 示图3已知:如图3 ,AD∥BC,AD=CB,AE=CF
求证:AFD≌△CEB 证明:∵AD∥BC(已知)
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE
在△AFD 和△CEB 中AD=CB(已知)
∠A=∠C(已证)
AF=CE(已证)
∴△AFD≌△CEB(SAS)分析:本题已知中的前两个条件,与例2相同,但是没有另一组夹边对应相等的条件,不难发现图3是由图2平移而得。利用AE=CF,可得:AF=CE变式训练1.图5变式训练2 已知:如图5:AB=AC,AD=AE,∠1=∠2
求证:△ABD≌△ACE证明:∵∠1=∠2(已知)
∴∠1+∠BAE = ∠2+∠BAE(等式性质)
即 ∠CAE= ∠BAD在△CAE和△BAD 中 AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(ASA)分析:两组对应夹边已知,缺少
对应夹角相等的条件。
由∠BAE 是两个三角形的
公共部分,可得:∠CAE=∠BAD。变式训练2:拓 展(1)求证:∠B=∠D
(2)若△ACE绕点A逆时针旋转,使∠1=900时,直线EC,BD的位置关系如何?给出证明。当∠EAD 为平角时呢?图5已知:如图5:AB=AC,AD=AE,∠1=∠2 12例2: 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。AB范例学习 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC ∴△ACB≌△DCE∴AB=DE在△ACB和△DCE中BCDEA 例3:如图,已知AB=AC,AD=AE。
求证:∠B=∠CCEABAD证明:在△ABD和△ACE中∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)范例学习例4:已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBDAB=CB(已知)∠ABD= ∠CBD(已知)?ABCD练习 (1)已知:如图, AB=CB ,∠ ABD= ∠ CBD
问AD=CD, BD 平分∠ ADC 吗?ABCD练习 (2) 已知:AD=CD, BD 平分∠ ADC 。
问∠A=∠ C 吗?例5:?已知:点A、E、F、C在同一条直线上, AD=CB,AD∥CB,AE=CF.
求证:EB∥DF ADBCEF证明:∵ AD∥CB(已知)∴ ∠A=∠C (两直线平行,内错角相等)∵ AE=CF (已知)∴ AE+EF=CF+EF (等式的性质) 即 AF=CE在△AFD与△CEB中AF=CE (已证)∠A=∠C (已证)AD=CB (已知)∴∴△AFD ≌ △CEB(SAS)∴ ∠AFD=∠CEB∴ EB∥DF FEDCBA例6:如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?解:全等。∵BD=EC(已知) ∴BD-CD=EC-CD。即BC=ED 在△ABC与△FED中∴△ABC≌△FED(SAS)AC∥FD吗?为什么?∴∠1=∠2( )∴∠3=∠4( )∴AC∥FD(内错角相等,两直线平行4321例7.(1) 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。证明:在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD(SAS)(已知)(已知)(公共边)∴BC=AD(全等三角形的对应边相等)(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。AE=AD (已知)
= ( )
AC = AB (已知)SAS解:在△AEC和△ADB中∴ △AEC≌△ADB( )∠A∠A公共角例8:如图在△ABC中,AB=AC, AD平分∠BAC,求证: △ABD≌△ACD.
证明: ∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
∴ △ABD≌△ACD(S.A.S.).
∵例9:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。解:在△EDH和△FDH中: ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)∴△EDH≌△FDH(S.A.S)
∴EH=FH(全等三角形对应边相等)
例10:已知:如图,AB=DB,CB=EB,∠1=∠2
求证:∠A=∠D证明:∵ ∠1=∠2(已知)
∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质)
即∠ABC=∠DBE
在△ABC和△DBE中,
AB=DB(已知)
∠ABC=∠DBE(已证)
CB=EB(已知)
∴△ABC≌△DBE(SAS)
∴ ∠A=∠D(全等三角形的对应角相等)1: 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由
∴△OAD≌△OBC (S.A.S) 解:在△OAD 和△OBC中巩固练习
2.?如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:(1)全等(2)全等巩固练习
巩固练习
3.点M是等腰梯形ABCD底边AB的中点,求证DM=CM,∠ADM=∠BCM.
证明:∵ 点M是等腰梯形ABCD底边AB的中点
∴ AD=BC (等腰梯形的两腰相等)
∠A=∠B(等腰梯形的两底角相等)
AM=BM (线段中点的定义)
在△ADM和△BCM中 AD=BC, (已证)
∠A=∠B, (已证)
AM=BM, (已证)
∴△AMD≌△BMC (S.A.S)∴ DM=CM(全等三角形的对应边相等)∠ADM=∠BCM (全等三角形的对应角相等)说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS)2、这说明三角形全等的条件中,你发现了什么?答:至少有一个条件:边相等注意哦!“边边角”不能判定两个三角形全等高汉光信辛中学
边角边ABCA'B'
C'
若△AOC≌△BOD,
对应边: AC= ,
AO= ,
CO= ,
对应角有: ∠A= ,
∠C= ,
∠AOC= ;
复习:全等三角形的性质BDBODO∠B∠D∠BOD操作第一组:一条边为6cm;
第二组:一个角是45°;
第三组:两条边分别为4cm和6cm;
第四组:一条边为6cm,一个角为45°;
第五组:两个角分别为45°和60°.
按下列条件做三角形,并通过比较判断它们之间是否全等,由此你有什么发现?大家要合作哦探究1对于三个角对应相等的两个三角形全等吗?如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。三个角对应相等的两个三角形不一定全等 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2注:这个角一定要是这两边所夹的角做一做:画△ABC,使AB=3cm,AC=4cm。画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?探究3先任意画出一个△ABC,再画出一个△A′B′C′使A′B′=AB,A′C′=AC,∠A=∠A′。画法:2. 在射线A′D上截取A′B′= AB3. 在射线A′E上截取A′C′=AC1. 画∠DA′E= ∠A4.连接B′C′∴△A′B′C′就是所求的三角形把你们所画的三角形剪下来与原来的三角形进行比较,它们能互相重合吗?探究4问:如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则它们完全重合?即△ABC≌△ DEF ?问:如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则它们完全重合?即△ABC≌△ DEF ? 三角形全等判定方法1用符号语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
44练一练:1.如图,在下列三角形中,哪两个三角形全等?445530°30°4430°4640°4640°40°①③②⑥⑤④2.在下列图中找出全等三角形,并把它们用直线连起来.已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA分析:观察图形,结合已知条件,知,AD=CB,AC=CA,但没有给出两组对应边的夹角(∠1,∠2)相等。所以,应设法先证明∠1=∠2,才能使全等条件充足。AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)例1:证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中DC1AB2B范例学习动 态 演 示图3已知:如图3 ,AD∥BC,AD=CB,AE=CF
求证:AFD≌△CEB 证明:∵AD∥BC(已知)
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE
在△AFD 和△CEB 中AD=CB(已知)
∠A=∠C(已证)
AF=CE(已证)
∴△AFD≌△CEB(SAS)分析:本题已知中的前两个条件,与例2相同,但是没有另一组夹边对应相等的条件,不难发现图3是由图2平移而得。利用AE=CF,可得:AF=CE变式训练1.图5变式训练2 已知:如图5:AB=AC,AD=AE,∠1=∠2
求证:△ABD≌△ACE证明:∵∠1=∠2(已知)
∴∠1+∠BAE = ∠2+∠BAE(等式性质)
即 ∠CAE= ∠BAD在△CAE和△BAD 中 AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(ASA)分析:两组对应夹边已知,缺少
对应夹角相等的条件。
由∠BAE 是两个三角形的
公共部分,可得:∠CAE=∠BAD。变式训练2:拓 展(1)求证:∠B=∠D
(2)若△ACE绕点A逆时针旋转,使∠1=900时,直线EC,BD的位置关系如何?给出证明。当∠EAD 为平角时呢?图5已知:如图5:AB=AC,AD=AE,∠1=∠2 12例2: 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。AB范例学习 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC ∴△ACB≌△DCE∴AB=DE在△ACB和△DCE中BCDEA 例3:如图,已知AB=AC,AD=AE。
求证:∠B=∠CCEABAD证明:在△ABD和△ACE中∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)范例学习例4:已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBDAB=CB(已知)∠ABD= ∠CBD(已知)?ABCD练习 (1)已知:如图, AB=CB ,∠ ABD= ∠ CBD
问AD=CD, BD 平分∠ ADC 吗?ABCD练习 (2) 已知:AD=CD, BD 平分∠ ADC 。
问∠A=∠ C 吗?例5:?已知:点A、E、F、C在同一条直线上, AD=CB,AD∥CB,AE=CF.
求证:EB∥DF ADBCEF证明:∵ AD∥CB(已知)∴ ∠A=∠C (两直线平行,内错角相等)∵ AE=CF (已知)∴ AE+EF=CF+EF (等式的性质) 即 AF=CE在△AFD与△CEB中AF=CE (已证)∠A=∠C (已证)AD=CB (已知)∴∴△AFD ≌ △CEB(SAS)∴ ∠AFD=∠CEB∴ EB∥DF FEDCBA例6:如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?解:全等。∵BD=EC(已知) ∴BD-CD=EC-CD。即BC=ED 在△ABC与△FED中∴△ABC≌△FED(SAS)AC∥FD吗?为什么?∴∠1=∠2( )∴∠3=∠4( )∴AC∥FD(内错角相等,两直线平行4321例7.(1) 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。证明:在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△BAD(SAS)(已知)(已知)(公共边)∴BC=AD(全等三角形的对应边相等)(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。AE=AD (已知)
= ( )
AC = AB (已知)SAS解:在△AEC和△ADB中∴ △AEC≌△ADB( )∠A∠A公共角例8:如图在△ABC中,AB=AC, AD平分∠BAC,求证: △ABD≌△ACD.
证明: ∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
∴ △ABD≌△ACD(S.A.S.).
∵例9:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。解:在△EDH和△FDH中: ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)∴△EDH≌△FDH(S.A.S)
∴EH=FH(全等三角形对应边相等)
例10:已知:如图,AB=DB,CB=EB,∠1=∠2
求证:∠A=∠D证明:∵ ∠1=∠2(已知)
∴∠1+∠DBC= ∠2+ ∠DBC(等式的性质)
即∠ABC=∠DBE
在△ABC和△DBE中,
AB=DB(已知)
∠ABC=∠DBE(已证)
CB=EB(已知)
∴△ABC≌△DBE(SAS)
∴ ∠A=∠D(全等三角形的对应角相等)1: 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由
∴△OAD≌△OBC (S.A.S) 解:在△OAD 和△OBC中巩固练习
2.?如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:(1)全等(2)全等巩固练习
巩固练习
3.点M是等腰梯形ABCD底边AB的中点,求证DM=CM,∠ADM=∠BCM.
证明:∵ 点M是等腰梯形ABCD底边AB的中点
∴ AD=BC (等腰梯形的两腰相等)
∠A=∠B(等腰梯形的两底角相等)
AM=BM (线段中点的定义)
在△ADM和△BCM中 AD=BC, (已证)
∠A=∠B, (已证)
AM=BM, (已证)
∴△AMD≌△BMC (S.A.S)∴ DM=CM(全等三角形的对应边相等)∠ADM=∠BCM (全等三角形的对应角相等)说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS)2、这说明三角形全等的条件中,你发现了什么?答:至少有一个条件:边相等注意哦!“边边角”不能判定两个三角形全等高汉光信辛中学
