北师大版2021-2022年初中数学九年级下册3.3垂径定理 自主达标测试(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学九年级下册3.3垂径定理 自主达标测试(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 13:50:01 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3-3垂径定理》自主达标测试(附答案)
一.选择题(共10小题,满分30分)
1.如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为( )
A.1 B.2 C.3 D.4
2.如图,△ABC中,AB=10,AC=8,BC=4,以点A为圆心,AB为半径作圆,交BC的延长线于点D,则CD长为( )
A.10 B.9 C.4 D.8
3.如图,在⊙O中,OC⊥AB于点C.若⊙O的半径为10,AB=16,则OC的长为( )
A.4 B.5 C.6 D.8
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A.5.8 B.3.8 C.1.3 D.2.5
5.如图,CD是圆O的直径,AB是圆O的弦,且AB=10,若CD⊥AB于点E,则AE的长为( )
A.4 B.5 C.6 D.8
6.如图,弦CD垂直于⊙O的直径AB,垂足为H,且OB=13,CD=24,则OH的长是( )
A.3 B.4 C.5 D.6
7.如图,AB为⊙O的直径,CD为⊙O的弦,CD⊥AB,垂足为E,OE=3,CD=8,AB=( )
A. B.10 C. D.5
8.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( )
A.4m B.6m C.8m D.10m
9.在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )
A.1分米 B.4分米
C.3分米 D.1分米或7分米
10.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2cm B.2.5cm C.3cm D.4cm
二.填空题(共10小题,满分30分)
11.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=1,CD=4,则OC的长为 .
13.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为 .
14.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
15.如图,在⊙O中,弦AB长为8.点O到AB的距离OE是3,则⊙O的半径OA= .
16.在直径为200cm的圆柱形油箱内装入一些油以后,截面如图(油面在圆心下):若油面的宽AB=160cm,则油的最大深度为 .
17.某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备 cm内径的管道(内径指内部直径).
18.如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为 cm.
19.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为 m.
20.残的圆形工件上量得一条弦BC=8,的中点D到BC的距离ED=2,则这个圆形工件的半径是 .
三.解答题(共7小题,满分60分)
21.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.
22.如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.
23.如图,紧挨着的三个正方形依次排列在半圆的直径上,且各有一个顶点在弧上,若两侧两个小正方形边长分别为2和3,求该半圆的半径.
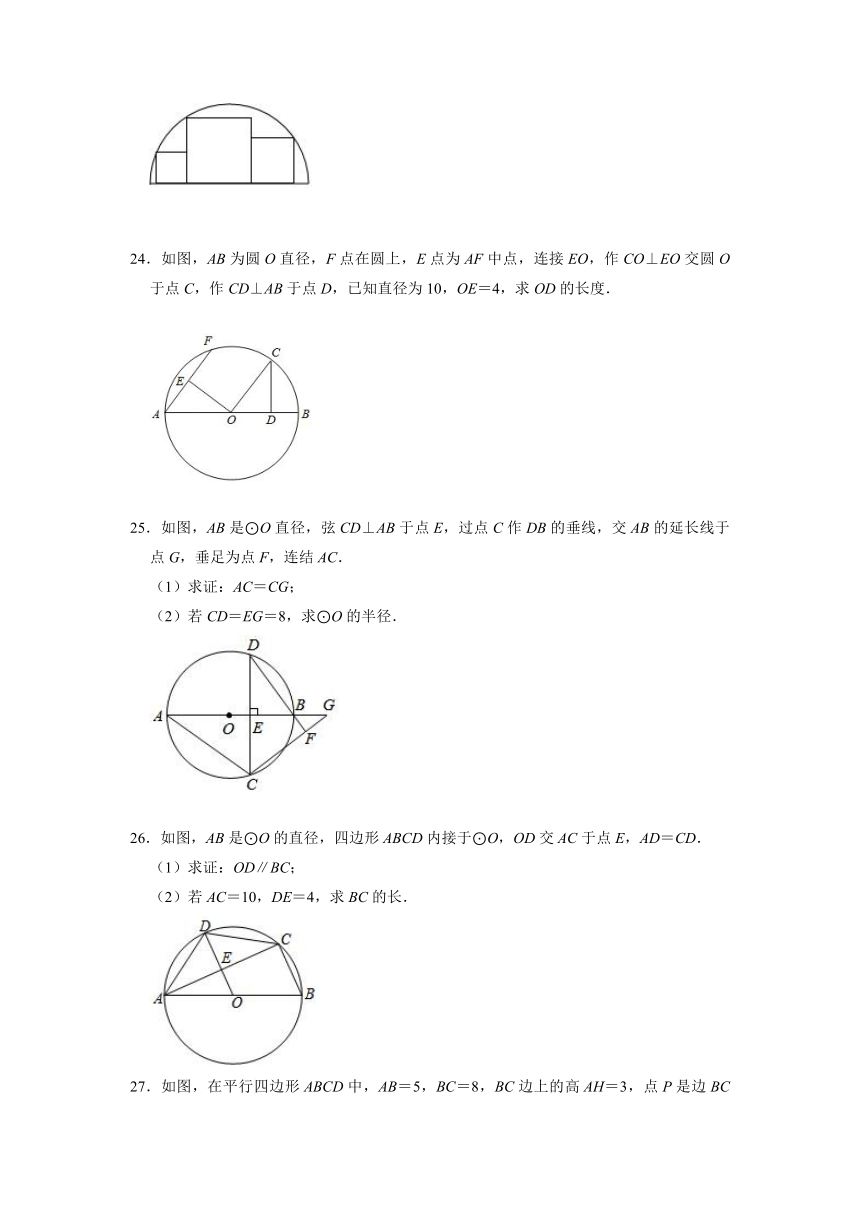
24.如图,AB为圆O直径,F点在圆上,E点为AF中点,连接EO,作CO⊥EO交圆O于点C,作CD⊥AB于点D,已知直径为10,OE=4,求OD的长度.
25.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
26.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
27.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵⊙O的半径为5,弦AB=8,点C是AB的中点,
∴OC⊥AB,AC=BC=4,OA=5,
∴OC===3,
故选:C.
2.解:过A作AE⊥BC于E,如图:
Rt△ABE中,AE2+BE2=AB2,
而AB=10,BC=4,
∴AE2=102﹣(4+CE)2=84﹣CE2﹣8CE,
Rt△ACE中,AE2=AC2﹣CE2,
而AC=8,
∴AE2=64﹣CE2,
∴84﹣CE2﹣8CE=64﹣CE2,
解得CE=2.5,
∴BE=6.5,
∴BD=2BE=13,
∴CD=9,
故选:B.
3.解:如图,连接OA.
∵OC⊥AB,
∴AC=CB=AB=8,
∵OA=10,∠ACO=90°,
∴OC===6,
故选:C.
4.解:过O点作OH⊥AB于H,连接OA,如图,则AH=BH=AB=4,
在Rt△OAH中,OH===3,
所以OP的范围为3≤O<5.
故选:B.
5.解:∵CD⊥AB,CD是直径,
∴AE=EB=AB=5,
故选:B.
6.解:连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CH=CD=12,
在Rt△OCH中,OH===5,
故选:C.
7.解:∵CD⊥AB且AB为直径,CD=8,
∴,
连接CO,
∵在 Rt△COE中,OE=3,CE=4,
∴,
∴AB=2CO=10,
故选:B.
8.解:根据垂径定理可知AD=8,
在直角△AOD中,根据勾股定理得:
OA2=AD2+OD2
则102=82+(10﹣CD)2
解得:CD=16或4,
根据题中OA=10m,可知CD=16不合题意,故舍去,
所以取CD=4m.
故选:A.
9.解:连接OA.作OG⊥AB于G,
则在直角△OAG中,AG=3分米,
因为OA=5cm,根据勾股定理得到:OG=4分米,即弦AB的弦心距是4分米,
同理当油面宽AB为8分米时,弦心距是3分米,
当油面没超过圆心O时,油上升了1分米;当油面超过圆心O时,油上升了7分米.
因而油上升了1分米或7分米.
故选:D.
10.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
二.填空题(共10小题,满分30分)
11.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
12.解:∵弦CD⊥AB于点E,
∴CE=DE=CD=2,
设OC=r,则OE=OA﹣AE=r﹣1,
在Rt△COE中,(r﹣1)2+22=r2,解得r=,
即OC的长为.
故答案为.
13.解:连接OD,
∵CD⊥AB于点E,直径AB过O,
∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,
即⊙O的半径为5.
故答案为:5.
14.解:过点O作OH⊥CD于H,连接OC,如图,则CH=DH=CD=4,
在Rt△OCH中,OH==3,
所以CD与AB之间的距离是3.
故答案为3.
15.解:∵点O到AB的距离OE是3,
∴∠AEO=90°,AE=BE=4,
∴在Rt△AEO中
AO===5.
故答案为:5.
16.40cm解:连接OA,过点O作OE⊥AB,交AB于点M,
∵直径为200cm,AB=160cm,
∴OA=OE=100cm,AM=80cm,
∴OM===60cm,
∴ME=OE﹣OM=100﹣60=40cm.
故答案为40cm.
17.解:如图,过O作OC⊥AB于C,连接AO,
∴AC=AB=×60=30,
CO=AO﹣10,
在Rt△AOC中,AO2=AC2+OC2,
AO2=302+(AO﹣10)2,
解得AO=50cm.
∴内径为2×50=100cm.
故答案为:100.
18.解:作OE垂直AB于E交⊙O与D,
设OB=r,
根据垂径定理,BE=AB=3,
根据题意列方程得:(3.25﹣DE)2+9=3.252,
解得:DE=2,
∴该直尺的宽度为2cm.
故答案为:2.
19.解:∵OC⊥AB,
∴∠ADO=90°,AD=AB=8,
在Rt△AOD中,OD2=OA2﹣AD2,
∴OD==6,
∴CD=10﹣6=4(m).
故答案是4.
20.解:∵DE⊥BC,DE平分弧BC,
∴圆心在直线DE上,
设圆心为0,如图,连接OB,设圆的半径为R,则OE=R﹣DE=R﹣2,
∵OE⊥BC,
∴BE=CE=BC=×8=4,
在Rt△OEB中,OB2=BE2+OE2,即R2=42+(R﹣2)2,解得R=5,
即这个圆形工件的半径是5.
故答案为:5.
三.解答题(共7小题,满分60分)
21.解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB﹣OE=4﹣.
22.解:连接OC.
∵AB是半圆O的直径,
∴OC=OB=AB=×12=6.
∴OD=OB﹣DB=6﹣4=2,
∴在直角△OCD中,CD===4.
23.解:如图,延长DF交⊙O于M,连接CO,DN,EN,MN,DO.
∵AB⊥DM,
∴DF=FM,
∵DF=FN,
∴FD=FN=FM,
∴∠DNM=90°,
∴∠DNF=∠FNM=∠M=45°,
∵∠ENK=45°,
∴E、N、M共线,
∴∠DOE=2∠DME=90°,
∵∠DOF+∠ODF=90°,∠DOF+∠EOK=90°,
∴∠ODF=∠EOK,
在△DOF和△EOK中,
,
∴△DOF≌△EOK(AAS),
∴OF=EK=3,
∴OA=2+3=5,
在Rt△AOC中,CO===;
故该半圆的半径为.
24.解:∵E点为AF中点,
∴OE⊥AF,
∵CO⊥EO,
∴OC∥AF,
∴∠OAE=∠COD,
∵CD⊥AB,
∴∠AEO=∠ODC,
在△AEO和△ODC中,
,
∴△AEO≌△ODC(AAS),
∴CD=OE=4,
∵OC=5,
∴OD===3.
25.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
26.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
27.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
一.选择题(共10小题,满分30分)
1.如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为( )
A.1 B.2 C.3 D.4
2.如图,△ABC中,AB=10,AC=8,BC=4,以点A为圆心,AB为半径作圆,交BC的延长线于点D,则CD长为( )
A.10 B.9 C.4 D.8
3.如图,在⊙O中,OC⊥AB于点C.若⊙O的半径为10,AB=16,则OC的长为( )
A.4 B.5 C.6 D.8
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A.5.8 B.3.8 C.1.3 D.2.5
5.如图,CD是圆O的直径,AB是圆O的弦,且AB=10,若CD⊥AB于点E,则AE的长为( )
A.4 B.5 C.6 D.8
6.如图,弦CD垂直于⊙O的直径AB,垂足为H,且OB=13,CD=24,则OH的长是( )
A.3 B.4 C.5 D.6
7.如图,AB为⊙O的直径,CD为⊙O的弦,CD⊥AB,垂足为E,OE=3,CD=8,AB=( )
A. B.10 C. D.5
8.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( )
A.4m B.6m C.8m D.10m
9.在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,当油面宽变为8分米,油面AB上升( )
A.1分米 B.4分米
C.3分米 D.1分米或7分米
10.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2cm B.2.5cm C.3cm D.4cm
二.填空题(共10小题,满分30分)
11.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=1,CD=4,则OC的长为 .
13.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为 .
14.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
15.如图,在⊙O中,弦AB长为8.点O到AB的距离OE是3,则⊙O的半径OA= .
16.在直径为200cm的圆柱形油箱内装入一些油以后,截面如图(油面在圆心下):若油面的宽AB=160cm,则油的最大深度为 .
17.某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备 cm内径的管道(内径指内部直径).
18.如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为 cm.
19.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为 m.
20.残的圆形工件上量得一条弦BC=8,的中点D到BC的距离ED=2,则这个圆形工件的半径是 .
三.解答题(共7小题,满分60分)
21.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,求BE的长.
22.如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.
23.如图,紧挨着的三个正方形依次排列在半圆的直径上,且各有一个顶点在弧上,若两侧两个小正方形边长分别为2和3,求该半圆的半径.
24.如图,AB为圆O直径,F点在圆上,E点为AF中点,连接EO,作CO⊥EO交圆O于点C,作CD⊥AB于点D,已知直径为10,OE=4,求OD的长度.
25.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
26.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
27.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵⊙O的半径为5,弦AB=8,点C是AB的中点,
∴OC⊥AB,AC=BC=4,OA=5,
∴OC===3,
故选:C.
2.解:过A作AE⊥BC于E,如图:
Rt△ABE中,AE2+BE2=AB2,
而AB=10,BC=4,
∴AE2=102﹣(4+CE)2=84﹣CE2﹣8CE,
Rt△ACE中,AE2=AC2﹣CE2,
而AC=8,
∴AE2=64﹣CE2,
∴84﹣CE2﹣8CE=64﹣CE2,
解得CE=2.5,
∴BE=6.5,
∴BD=2BE=13,
∴CD=9,
故选:B.
3.解:如图,连接OA.
∵OC⊥AB,
∴AC=CB=AB=8,
∵OA=10,∠ACO=90°,
∴OC===6,
故选:C.
4.解:过O点作OH⊥AB于H,连接OA,如图,则AH=BH=AB=4,
在Rt△OAH中,OH===3,
所以OP的范围为3≤O<5.
故选:B.
5.解:∵CD⊥AB,CD是直径,
∴AE=EB=AB=5,
故选:B.
6.解:连接OC,
∵AB是⊙O的直径,CD⊥AB,
∴CH=CD=12,
在Rt△OCH中,OH===5,
故选:C.
7.解:∵CD⊥AB且AB为直径,CD=8,
∴,
连接CO,
∵在 Rt△COE中,OE=3,CE=4,
∴,
∴AB=2CO=10,
故选:B.
8.解:根据垂径定理可知AD=8,
在直角△AOD中,根据勾股定理得:
OA2=AD2+OD2
则102=82+(10﹣CD)2
解得:CD=16或4,
根据题中OA=10m,可知CD=16不合题意,故舍去,
所以取CD=4m.
故选:A.
9.解:连接OA.作OG⊥AB于G,
则在直角△OAG中,AG=3分米,
因为OA=5cm,根据勾股定理得到:OG=4分米,即弦AB的弦心距是4分米,
同理当油面宽AB为8分米时,弦心距是3分米,
当油面没超过圆心O时,油上升了1分米;当油面超过圆心O时,油上升了7分米.
因而油上升了1分米或7分米.
故选:D.
10.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
二.填空题(共10小题,满分30分)
11.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
12.解:∵弦CD⊥AB于点E,
∴CE=DE=CD=2,
设OC=r,则OE=OA﹣AE=r﹣1,
在Rt△COE中,(r﹣1)2+22=r2,解得r=,
即OC的长为.
故答案为.
13.解:连接OD,
∵CD⊥AB于点E,直径AB过O,
∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,
即⊙O的半径为5.
故答案为:5.
14.解:过点O作OH⊥CD于H,连接OC,如图,则CH=DH=CD=4,
在Rt△OCH中,OH==3,
所以CD与AB之间的距离是3.
故答案为3.
15.解:∵点O到AB的距离OE是3,
∴∠AEO=90°,AE=BE=4,
∴在Rt△AEO中
AO===5.
故答案为:5.
16.40cm解:连接OA,过点O作OE⊥AB,交AB于点M,
∵直径为200cm,AB=160cm,
∴OA=OE=100cm,AM=80cm,
∴OM===60cm,
∴ME=OE﹣OM=100﹣60=40cm.
故答案为40cm.
17.解:如图,过O作OC⊥AB于C,连接AO,
∴AC=AB=×60=30,
CO=AO﹣10,
在Rt△AOC中,AO2=AC2+OC2,
AO2=302+(AO﹣10)2,
解得AO=50cm.
∴内径为2×50=100cm.
故答案为:100.
18.解:作OE垂直AB于E交⊙O与D,
设OB=r,
根据垂径定理,BE=AB=3,
根据题意列方程得:(3.25﹣DE)2+9=3.252,
解得:DE=2,
∴该直尺的宽度为2cm.
故答案为:2.
19.解:∵OC⊥AB,
∴∠ADO=90°,AD=AB=8,
在Rt△AOD中,OD2=OA2﹣AD2,
∴OD==6,
∴CD=10﹣6=4(m).
故答案是4.
20.解:∵DE⊥BC,DE平分弧BC,
∴圆心在直线DE上,
设圆心为0,如图,连接OB,设圆的半径为R,则OE=R﹣DE=R﹣2,
∵OE⊥BC,
∴BE=CE=BC=×8=4,
在Rt△OEB中,OB2=BE2+OE2,即R2=42+(R﹣2)2,解得R=5,
即这个圆形工件的半径是5.
故答案为:5.
三.解答题(共7小题,满分60分)
21.解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB﹣OE=4﹣.
22.解:连接OC.
∵AB是半圆O的直径,
∴OC=OB=AB=×12=6.
∴OD=OB﹣DB=6﹣4=2,
∴在直角△OCD中,CD===4.
23.解:如图,延长DF交⊙O于M,连接CO,DN,EN,MN,DO.
∵AB⊥DM,
∴DF=FM,
∵DF=FN,
∴FD=FN=FM,
∴∠DNM=90°,
∴∠DNF=∠FNM=∠M=45°,
∵∠ENK=45°,
∴E、N、M共线,
∴∠DOE=2∠DME=90°,
∵∠DOF+∠ODF=90°,∠DOF+∠EOK=90°,
∴∠ODF=∠EOK,
在△DOF和△EOK中,
,
∴△DOF≌△EOK(AAS),
∴OF=EK=3,
∴OA=2+3=5,
在Rt△AOC中,CO===;
故该半圆的半径为.
24.解:∵E点为AF中点,
∴OE⊥AF,
∵CO⊥EO,
∴OC∥AF,
∴∠OAE=∠COD,
∵CD⊥AB,
∴∠AEO=∠ODC,
在△AEO和△ODC中,
,
∴△AEO≌△ODC(AAS),
∴CD=OE=4,
∵OC=5,
∴OD===3.
25.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
26.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
27.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
