北师大版2021-2022年初中数学九年级下册1.5三角函数的应用 同步课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学九年级下册1.5三角函数的应用 同步课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 620.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 13:50:07 | ||
图片预览




文档简介
2021-2022年初中数学九年级下册同步(北师大版)
1.5三角函数的应用-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在Rt△ABC中,∠C=90°,cosA=,则sinA=( )
A. B. C. D.
2.⊿ABC中,∠C=90°,CD⊥AB于D,下列比值中不等于的是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A. B. C. D.
4.如图,矩形的对角线交于点O,已知则下列结论错误的是( )
A. B.
C. D.
5.甲、乙、丙三人放风筝,各人放出的风筝线分别为,线与地平面所成的角分别为,假设风筝线近似看作是拉直的,则所放风筝最高的是( ).
A.甲 B.乙 C.丙 D.无法确定
6.如图,在中,于点,若,则的值为( )
A. B. C. D.
二、填空题
7.在Rt△ABC中,∠C=90°,若,则的值为 _______
8.在中,∠C=90°,AB=13,AC=5,______.
9.某人沿着坡度为的山坡向上走,这时他离水平地面______.
10.化简:(其中)=___________.
11.①sin2A+cos2A=________,②tanA cotA=________.
12.下列结论中(其中,均为锐角),正确的是___________.(填序号)
①;②;③当时,;④.
三、解答题
13.若α为锐角,试证明:.
14.在中,,与有什么关系?
15.如图,斜坡AC的坡度为1:,AC=8米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=8米,试求旗杆BC的高度.
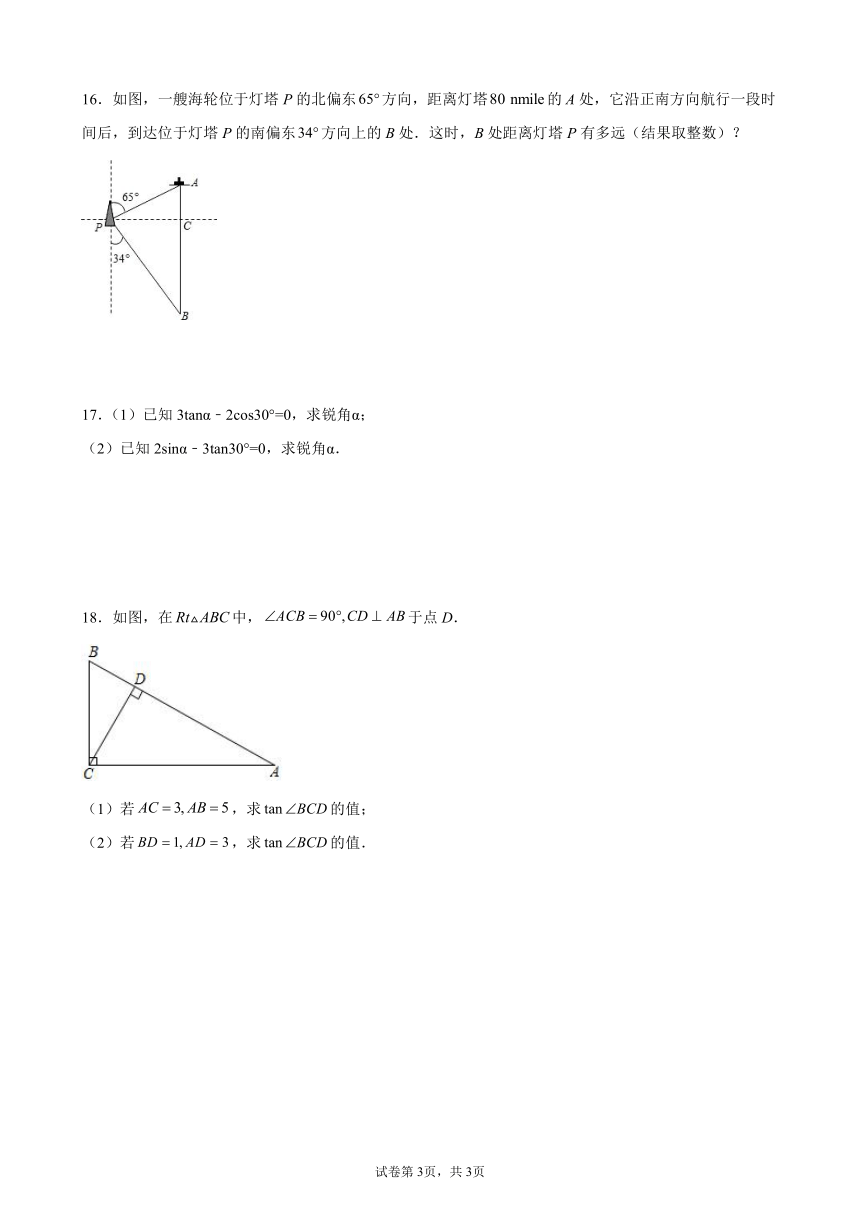
16.如图,一艘海轮位于灯塔P的北偏东方向,距离灯塔的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东方向上的B处.这时,B处距离灯塔P有多远(结果取整数)?
17.(1)已知3tanα﹣2cos30°=0,求锐角α;
(2)已知2sinα﹣3tan30°=0,求锐角α.
18.如图,在中,于点D.
(1)若,求的值;
(2)若,求的值.
参考答案
1.C
【解析】解:∵sin2A+cos2A=1,即sin2A+()2=1,
∴sin2A=,
∴sinA=或sinA=﹣(舍去),
∴sinA=,
故选:C.
2.D
【解析】解:如下图所示
在Rt中,=,故A不符合题意;
在Rt中,=,故B不符合题意;
∵∠A+∠ACD=90°,∠BCD+∠ACD=90°
∴∠A=∠BCD
∴=tan∠BCD=,故C不符合题意;
≠,故D符合题意.
故选D.
3.A
【解析】解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA ,∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
4.C
【解析】选项A,∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,AC=BD,AO=CO,BO=DO,
∴AO=OB=CO=DO,
∴∠DBC=∠ACB,
∴由三角形内角和定理得:∠BAC=∠BDC=∠α,
选项A正确;
选项B,在Rt△ABC中,tanα=,
即BC=m tanα,
选项B正确;
选项C,在Rt△ABC中,AC=,即AO=,
选项C错误;
选项D,∵四边形ABCD是矩形,
∴DC=AB=m,
∵∠BAC=∠BDC=α,
∴在Rt△DCB中,BD=,
选项D正确.
故选C.
5.B
【解析】解:根据三角函数的定义可以得到,甲、乙、丙三人风筝的高度分别为、、,
,
,
∵
∴所放风筝最高的是乙
故选为B
6.B
【解析】∵在中,,
∴,
∵于点,
∴,
∴,,
∴∽,
∴,即,,
∵,
∴设,,
∴,
∴,
故选:B.
7.
【解析】解:∵,,
∴∠B=60°,
∴∠A=30°,
∴sinA=.
故答案为:
8.
【解析】解:中,,
.
故答案为:.
9.
【解析】解:如图所示:
.
.
,
.
故答案为:25.
10.或或0
【解析】解:∵,
∴①当时,=;
②当是,=;
③当时,=,
故答案为:或或0.
11.1 1
【解析】如图,设Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为,
则sinA= ,cosA=,tanA=,cotA=,,
∴(1)sin2A+cos2A=;
(2)tanA cotA=.
12.①③④
【解析】解:①如图,在中,
∵,,
∴,故①正确;
②若,则,
,
∴
∴,故②错误;
③当时,,
∴越大,对边越大,且越接近斜边,
∴越大,
∴当时,,故③正确;
④∵,,,
∴,故④正确.
故答案为:①③④.
13.证明见解析.
【解析】证明:如图,
中,∠C=90°,设∠A=α,
则 ∴
又 ∵ ∴.
14.
【解析】解:在中,,
∴,,
∴,
答:.
15.旗杆BC的高度为8米
【解析】解: 延长交于点,则.
在中,AC=8,由坡度为可知:,
,
.
在中,.
,
(米.
答:旗杆的高度为8米.
16.当海轮到达位于灯塔P的南偏东方向时,它距离灯塔P大约
【解析】解:如图,在中,
.
在中,,
∵,
∴.
因此,当海轮到达位于灯塔P的南偏东方向时,它距离灯塔P大约.
17.(1)α=30°;(2)α=60°.
【解析】解:(1)解得:tanα=,
则α=30°;
(2)解得:sinα=,
则α=60°.
18.(1);(2)
【解析】(1)∵,
∵,
∴,在中,
,
∴,
∴;
(2)∵,
∴,
由(1)可知,
∴,∴,
∴,
∴,
∴.
试卷第2页,共3页
试卷第3页,共3页
1.5三角函数的应用-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在Rt△ABC中,∠C=90°,cosA=,则sinA=( )
A. B. C. D.
2.⊿ABC中,∠C=90°,CD⊥AB于D,下列比值中不等于的是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,sinA=,则sinB的值为( )
A. B. C. D.
4.如图,矩形的对角线交于点O,已知则下列结论错误的是( )
A. B.
C. D.
5.甲、乙、丙三人放风筝,各人放出的风筝线分别为,线与地平面所成的角分别为,假设风筝线近似看作是拉直的,则所放风筝最高的是( ).
A.甲 B.乙 C.丙 D.无法确定
6.如图,在中,于点,若,则的值为( )
A. B. C. D.
二、填空题
7.在Rt△ABC中,∠C=90°,若,则的值为 _______
8.在中,∠C=90°,AB=13,AC=5,______.
9.某人沿着坡度为的山坡向上走,这时他离水平地面______.
10.化简:(其中)=___________.
11.①sin2A+cos2A=________,②tanA cotA=________.
12.下列结论中(其中,均为锐角),正确的是___________.(填序号)
①;②;③当时,;④.
三、解答题
13.若α为锐角,试证明:.
14.在中,,与有什么关系?
15.如图,斜坡AC的坡度为1:,AC=8米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=8米,试求旗杆BC的高度.
16.如图,一艘海轮位于灯塔P的北偏东方向,距离灯塔的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东方向上的B处.这时,B处距离灯塔P有多远(结果取整数)?
17.(1)已知3tanα﹣2cos30°=0,求锐角α;
(2)已知2sinα﹣3tan30°=0,求锐角α.
18.如图,在中,于点D.
(1)若,求的值;
(2)若,求的值.
参考答案
1.C
【解析】解:∵sin2A+cos2A=1,即sin2A+()2=1,
∴sin2A=,
∴sinA=或sinA=﹣(舍去),
∴sinA=,
故选:C.
2.D
【解析】解:如下图所示
在Rt中,=,故A不符合题意;
在Rt中,=,故B不符合题意;
∵∠A+∠ACD=90°,∠BCD+∠ACD=90°
∴∠A=∠BCD
∴=tan∠BCD=,故C不符合题意;
≠,故D符合题意.
故选D.
3.A
【解析】解:∵Rt△ABC中,∠C=90°,sinA=,
∴cosA ,∠A+∠B=90°,
∴sinB=cosA=.
故选:A.
4.C
【解析】选项A,∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,AC=BD,AO=CO,BO=DO,
∴AO=OB=CO=DO,
∴∠DBC=∠ACB,
∴由三角形内角和定理得:∠BAC=∠BDC=∠α,
选项A正确;
选项B,在Rt△ABC中,tanα=,
即BC=m tanα,
选项B正确;
选项C,在Rt△ABC中,AC=,即AO=,
选项C错误;
选项D,∵四边形ABCD是矩形,
∴DC=AB=m,
∵∠BAC=∠BDC=α,
∴在Rt△DCB中,BD=,
选项D正确.
故选C.
5.B
【解析】解:根据三角函数的定义可以得到,甲、乙、丙三人风筝的高度分别为、、,
,
,
∵
∴所放风筝最高的是乙
故选为B
6.B
【解析】∵在中,,
∴,
∵于点,
∴,
∴,,
∴∽,
∴,即,,
∵,
∴设,,
∴,
∴,
故选:B.
7.
【解析】解:∵,,
∴∠B=60°,
∴∠A=30°,
∴sinA=.
故答案为:
8.
【解析】解:中,,
.
故答案为:.
9.
【解析】解:如图所示:
.
.
,
.
故答案为:25.
10.或或0
【解析】解:∵,
∴①当时,=;
②当是,=;
③当时,=,
故答案为:或或0.
11.1 1
【解析】如图,设Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为,
则sinA= ,cosA=,tanA=,cotA=,,
∴(1)sin2A+cos2A=;
(2)tanA cotA=.
12.①③④
【解析】解:①如图,在中,
∵,,
∴,故①正确;
②若,则,
,
∴
∴,故②错误;
③当时,,
∴越大,对边越大,且越接近斜边,
∴越大,
∴当时,,故③正确;
④∵,,,
∴,故④正确.
故答案为:①③④.
13.证明见解析.
【解析】证明:如图,
中,∠C=90°,设∠A=α,
则 ∴
又 ∵ ∴.
14.
【解析】解:在中,,
∴,,
∴,
答:.
15.旗杆BC的高度为8米
【解析】解: 延长交于点,则.
在中,AC=8,由坡度为可知:,
,
.
在中,.
,
(米.
答:旗杆的高度为8米.
16.当海轮到达位于灯塔P的南偏东方向时,它距离灯塔P大约
【解析】解:如图,在中,
.
在中,,
∵,
∴.
因此,当海轮到达位于灯塔P的南偏东方向时,它距离灯塔P大约.
17.(1)α=30°;(2)α=60°.
【解析】解:(1)解得:tanα=,
则α=30°;
(2)解得:sinα=,
则α=60°.
18.(1);(2)
【解析】(1)∵,
∵,
∴,在中,
,
∴,
∴;
(2)∵,
∴,
由(1)可知,
∴,∴,
∴,
∴,
∴.
试卷第2页,共3页
试卷第3页,共3页
