第六章 特殊平行四边形 单元测试题(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 单元测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
单元测试题
(满分:100分时间:60分钟)
一、选择题(每小题3分,共30分)
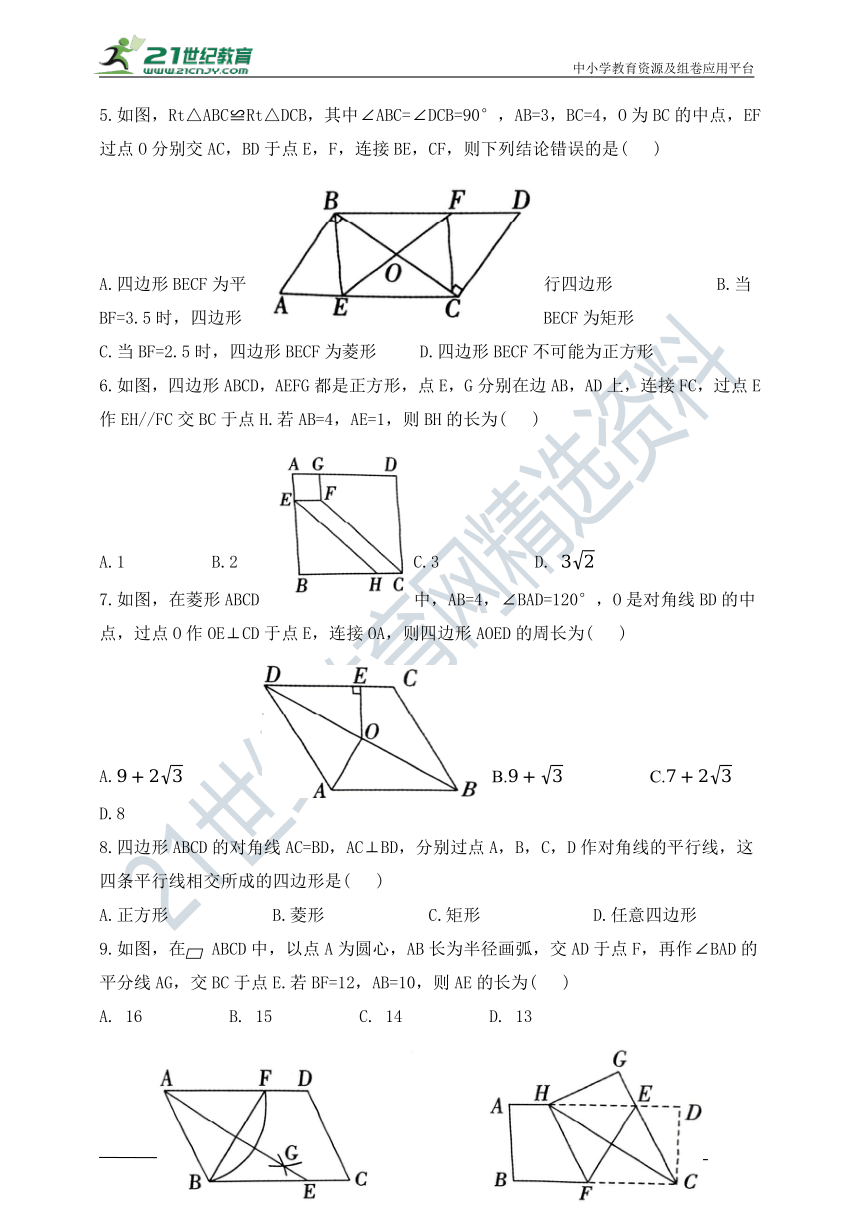
1.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AB,BC的中点,连接EF.若EF=3,BD=8,则菱形ABCD的边长为( )
A. 10 B.8 C.6 D.5
2.已知四边形ABCD是平行四边形,AC,BD相交于点O,则下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当△ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
3.如图,在Rt△ABC中,∠ACB=90°,CD为边AB上的高,CE为边AB上的中线,AD=2,CE=5,则CD的长为( )
A.2 B.3 C.4 D.
4.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD,PBEF,设∠CBE=α,则∠AFP的度数为( )
A.2α B.90°-α C.45°+α D.90°-
5.如图,Rt△ABC≌Rt△DCB,其中∠ABC=∠DCB=90°,AB=3,BC=4,O为BC的中点,EF过点O分别交AC,BD于点E,F,连接BE,CF,则下列结论错误的是( )
A.四边形BECF为平行四边形 B.当BF=3.5时,四边形BECF为矩形
C.当BF=2.5时,四边形BECF为菱形 D.四边形BECF不可能为正方形
6.如图,四边形ABCD,AEFG都是正方形,点E,G分别在边AB,AD上,连接FC,过点E作EH//FC交BC于点H.若AB=4,AE=1,则BH的长为( )
A.1 B.2 C.3 D.
7.如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连接OA,则四边形AOED的周长为( )
A. B. C. D.8
8.四边形ABCD的对角线AC=BD,AC⊥BD,分别过点A,B,C,D作对角线的平行线,这四条平行线相交所成的四边形是( )
A.正方形 B.菱形 C.矩形 D.任意四边形
9.如图,在 ABCD中,以点A为圆心,AB长为半径画弧,交AD于点F,再作∠BAD的平分线AG,交BC于点E.若BF=12,AB=10,则AE的长为( )
A. 16 B. 15 C. 14 D. 13
第9题 第10题
10.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C落在边AD上的点H处,点D落在点G处,有下列四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF长的取值范围是3≤BF≤4;④当点H与点A重合时,EF=2其中,正确的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
二、填空题(每小题3分,共18分)
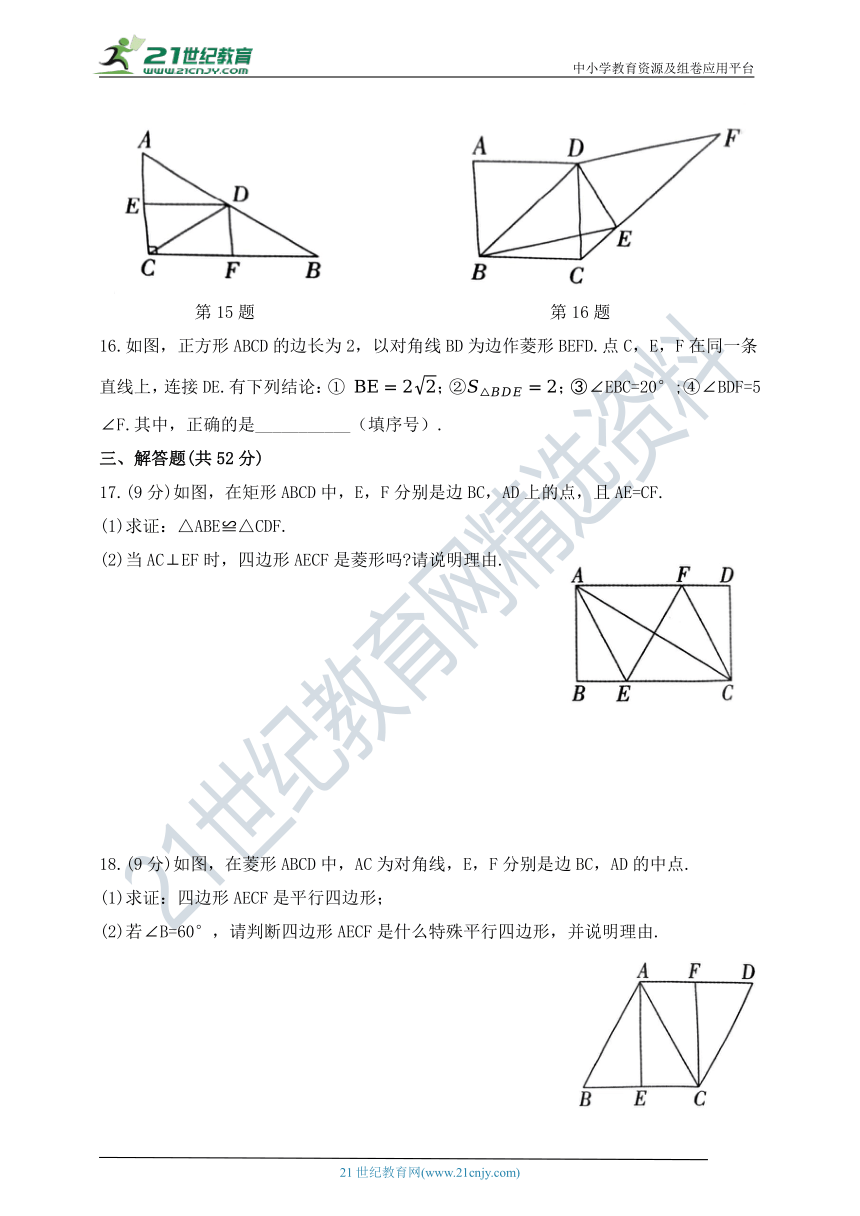
11.如图,在矩形ABCD中,DE⊥AC于点E,且∠ADE:∠EDC=2∶1,则∠BDE=________.
第11题 第12题
12.如图,在矩形ABCD中,AB=2,BC=4,E是矩形ABCD的边AD上的一动点,连接CE,以CE为边,在CE的右侧构造正方形CEFG,当AE=___________时,ED平分∠FEC.
13.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD,CB为边作 CDEB,当AD=________时, CDEB为菱形.
第13题 第14题
14.如图,O是矩形ABCD的对角线AC的中点,菱形ABEO的边长为2,则BC=________.
15.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,连接DE,DF,CD.如果_____________,那么四边形DECF是正方形(要求:①不再添加辅助线;②只需填一个符合要求的条件).
第15题 第16题
16.如图,正方形ABCD的边长为2,以对角线BD为边作菱形BEFD.点C,E,F在同一条直线上,连接DE.有下列结论:① ;②;③∠EBC=20°;④∠BDF=5∠F.其中,正确的是___________(填序号).
三、解答题(共52分)
17.(9分)如图,在矩形ABCD中,E,F分别是边BC,AD上的点,且AE=CF.
(1)求证:△ABE≌△CDF.
(2)当AC⊥EF时,四边形AECF是菱形吗 请说明理由.
18.(9分)如图,在菱形ABCD中,AC为对角线,E,F分别是边BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若∠B=60°,请判断四边形AECF是什么特殊平行四边形,并说明理由.
19.(10分)如图,E是正方形ABCD的边BC上的动点,∠AEF=90°,且EF=AE,FH⊥BH.
(1)求证:BE=CH;
(2)若AB=3,BE=x,用x表示DF的长.
20.(12分)在数学课上,老师请同学们思考如下问题:如图①,我们把一个四边形ABCD的四边中点依次连接起来,得到的四边形EFGH是平行四边形吗 小敏在思考问题时,有如下思路:如图①,连接AC.∵E,F分别是AB,BC的中点,∴EF//AC,EF=AC.∵G,H分别是CD,AD的中点,∴GH//AC,GH=AC.∴EF//GH,EF=GH.∴四边形EFGH是平行四边形.
(1)若只改变图①中四边形ABCD的形状(如图②),连接AC,BD,则四边形EFGH还是平行四边形吗?请说明理由(参考小敏思考问题的方法解决).
(2)如图②,在(1)的条件下:
①当AC与BD满足什么条件时,四边形EFGH是菱形 写出结论并证明.
②当AC与BD满足什么条件时,四边形EFGH是矩形 直接写出结论.
21.(12分)如图,在矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.
(1)若DG=2,求证:四边形EFGH是正方形;
(2)若DG=6,求△FCG的面积.
参考答案
一、1.D 2.B 3.C 4.B 5.B 6.C 7.B 8.A 9.A 10.C
二、11. 30 12. 2 13. 6 14. 15. 答案不唯一,如AC=BC
①②④
三、17.(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,AD//BC.
在Rt△ABE和Rt△CDF中,∴Rt△ABE≌Rt△CDF.
(2)当AC⊥EF时,四边形AECF是菱形
理由:∵△ABE≌△CDF,∴BE=DF.∵BC=AD,∴CE=AF.∵CE//AF,∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形.
18.(1)∵四边形ABCD是菱形,∴AB=BC=AD,AD//BC.∵E,F分别是边BC,AD的中点,∴.∴AF=CE.又∵AF//CE,∴四边形AECF是平行四边形.
(2)四边形AECF是矩形
理由:∵∠B=60°,AB=BC,∴△ABC是等边三角形.∵BE=EC,∴AE⊥BC,即∠AEC=90°.∴四边形AECF是矩形.
19.(1)∵四边形ABCD是正方形,∴∠B=90°,AB=BC.
∵FH⊥BH,∴∠H=90°=∠B,∥F=90°-∠FEH.∵∠AEF=90°,∴∠AEB=90°-∠FEH.
∴∠AEB=∠F.在△ABE和△EHF中, ∴△ABE≌△EHF.
∴EH=AB=BC,BE=FH.∴BC-EC=EH-EC,即BE=CH.
(2)如图,连接DF,过点F作FP⊥CD于点P,∵∠H=∠DCH=∠FPC=90°,∴四边形PCHF是矩形.由(1),知BE=FH=CH,∴四边形PCHF是正方形.∴PF=CP=CH=BE=x.∵DC=AB=3,∴DP=DC-CP=3-x.在Rt△DPF中,由勾股定理,得DF= .
20.(1)四边形EFGH还是平行四边形
理由:∵E是AB的中点,F是BC的中点,∴ AC.同理, C.∴EF//HG,EF=HG.∴四边形EFGH是平行四边形.
(2)①AC=BD 由(1),知四边形;EFGH是平行四边形,又∵AC,∴当AC=BD时,FG=HG.∴四边形EFGH是菱形; ②当AC⊥BD时,四边形EFGH是矩形.
21.(1)∵四边形ABCD是矩形,∴∠A=∠D=90°.∵四边形EFGH是菱形,∴HG=EH.
∵AH=2,DG=2,∴DG=AH.,在Rt△DHG和Rt△ABH中,∴Rt△DHG≌Rt△AEH,∴∠DHG=∠AEH.∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°.∴四边形EFGH是正方形.
(2)过点F作FQ⊥CD,交DC的延长线于点Q,连接GE.∴∠Q=90°.∴∠A=∠Q.
∵四边形ABCD是矩形,∴AB//CD.∴∠AEG=∠QGE,即∠AEH+∠HEG=∠QGF+∠FGE.∵四边形EFGH是菱形,∴HE=GF,HE//GF.∴∠HEG=∠FGE,∴∠AEH=∠QGF.
在△AEH和△QGF中,∴△AEH≌△QGF.∴AH=QF=2.
∵DG=6,CD=8,∴CG=2.∴△FCG的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
单元测试题
(满分:100分时间:60分钟)
一、选择题(每小题3分,共30分)
1.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AB,BC的中点,连接EF.若EF=3,BD=8,则菱形ABCD的边长为( )
A. 10 B.8 C.6 D.5
2.已知四边形ABCD是平行四边形,AC,BD相交于点O,则下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当△ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
3.如图,在Rt△ABC中,∠ACB=90°,CD为边AB上的高,CE为边AB上的中线,AD=2,CE=5,则CD的长为( )
A.2 B.3 C.4 D.
4.如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD,PBEF,设∠CBE=α,则∠AFP的度数为( )
A.2α B.90°-α C.45°+α D.90°-
5.如图,Rt△ABC≌Rt△DCB,其中∠ABC=∠DCB=90°,AB=3,BC=4,O为BC的中点,EF过点O分别交AC,BD于点E,F,连接BE,CF,则下列结论错误的是( )
A.四边形BECF为平行四边形 B.当BF=3.5时,四边形BECF为矩形
C.当BF=2.5时,四边形BECF为菱形 D.四边形BECF不可能为正方形
6.如图,四边形ABCD,AEFG都是正方形,点E,G分别在边AB,AD上,连接FC,过点E作EH//FC交BC于点H.若AB=4,AE=1,则BH的长为( )
A.1 B.2 C.3 D.
7.如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连接OA,则四边形AOED的周长为( )
A. B. C. D.8
8.四边形ABCD的对角线AC=BD,AC⊥BD,分别过点A,B,C,D作对角线的平行线,这四条平行线相交所成的四边形是( )
A.正方形 B.菱形 C.矩形 D.任意四边形
9.如图,在 ABCD中,以点A为圆心,AB长为半径画弧,交AD于点F,再作∠BAD的平分线AG,交BC于点E.若BF=12,AB=10,则AE的长为( )
A. 16 B. 15 C. 14 D. 13
第9题 第10题
10.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在边AD,BC上,将纸片ABCD沿直线EF折叠,点C落在边AD上的点H处,点D落在点G处,有下列四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF长的取值范围是3≤BF≤4;④当点H与点A重合时,EF=2其中,正确的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
二、填空题(每小题3分,共18分)
11.如图,在矩形ABCD中,DE⊥AC于点E,且∠ADE:∠EDC=2∶1,则∠BDE=________.
第11题 第12题
12.如图,在矩形ABCD中,AB=2,BC=4,E是矩形ABCD的边AD上的一动点,连接CE,以CE为边,在CE的右侧构造正方形CEFG,当AE=___________时,ED平分∠FEC.
13.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD,CB为边作 CDEB,当AD=________时, CDEB为菱形.
第13题 第14题
14.如图,O是矩形ABCD的对角线AC的中点,菱形ABEO的边长为2,则BC=________.
15.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,连接DE,DF,CD.如果_____________,那么四边形DECF是正方形(要求:①不再添加辅助线;②只需填一个符合要求的条件).
第15题 第16题
16.如图,正方形ABCD的边长为2,以对角线BD为边作菱形BEFD.点C,E,F在同一条直线上,连接DE.有下列结论:① ;②;③∠EBC=20°;④∠BDF=5∠F.其中,正确的是___________(填序号).
三、解答题(共52分)
17.(9分)如图,在矩形ABCD中,E,F分别是边BC,AD上的点,且AE=CF.
(1)求证:△ABE≌△CDF.
(2)当AC⊥EF时,四边形AECF是菱形吗 请说明理由.
18.(9分)如图,在菱形ABCD中,AC为对角线,E,F分别是边BC,AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若∠B=60°,请判断四边形AECF是什么特殊平行四边形,并说明理由.
19.(10分)如图,E是正方形ABCD的边BC上的动点,∠AEF=90°,且EF=AE,FH⊥BH.
(1)求证:BE=CH;
(2)若AB=3,BE=x,用x表示DF的长.
20.(12分)在数学课上,老师请同学们思考如下问题:如图①,我们把一个四边形ABCD的四边中点依次连接起来,得到的四边形EFGH是平行四边形吗 小敏在思考问题时,有如下思路:如图①,连接AC.∵E,F分别是AB,BC的中点,∴EF//AC,EF=AC.∵G,H分别是CD,AD的中点,∴GH//AC,GH=AC.∴EF//GH,EF=GH.∴四边形EFGH是平行四边形.
(1)若只改变图①中四边形ABCD的形状(如图②),连接AC,BD,则四边形EFGH还是平行四边形吗?请说明理由(参考小敏思考问题的方法解决).
(2)如图②,在(1)的条件下:
①当AC与BD满足什么条件时,四边形EFGH是菱形 写出结论并证明.
②当AC与BD满足什么条件时,四边形EFGH是矩形 直接写出结论.
21.(12分)如图,在矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.
(1)若DG=2,求证:四边形EFGH是正方形;
(2)若DG=6,求△FCG的面积.
参考答案
一、1.D 2.B 3.C 4.B 5.B 6.C 7.B 8.A 9.A 10.C
二、11. 30 12. 2 13. 6 14. 15. 答案不唯一,如AC=BC
①②④
三、17.(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,AD//BC.
在Rt△ABE和Rt△CDF中,∴Rt△ABE≌Rt△CDF.
(2)当AC⊥EF时,四边形AECF是菱形
理由:∵△ABE≌△CDF,∴BE=DF.∵BC=AD,∴CE=AF.∵CE//AF,∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形.
18.(1)∵四边形ABCD是菱形,∴AB=BC=AD,AD//BC.∵E,F分别是边BC,AD的中点,∴.∴AF=CE.又∵AF//CE,∴四边形AECF是平行四边形.
(2)四边形AECF是矩形
理由:∵∠B=60°,AB=BC,∴△ABC是等边三角形.∵BE=EC,∴AE⊥BC,即∠AEC=90°.∴四边形AECF是矩形.
19.(1)∵四边形ABCD是正方形,∴∠B=90°,AB=BC.
∵FH⊥BH,∴∠H=90°=∠B,∥F=90°-∠FEH.∵∠AEF=90°,∴∠AEB=90°-∠FEH.
∴∠AEB=∠F.在△ABE和△EHF中, ∴△ABE≌△EHF.
∴EH=AB=BC,BE=FH.∴BC-EC=EH-EC,即BE=CH.
(2)如图,连接DF,过点F作FP⊥CD于点P,∵∠H=∠DCH=∠FPC=90°,∴四边形PCHF是矩形.由(1),知BE=FH=CH,∴四边形PCHF是正方形.∴PF=CP=CH=BE=x.∵DC=AB=3,∴DP=DC-CP=3-x.在Rt△DPF中,由勾股定理,得DF= .
20.(1)四边形EFGH还是平行四边形
理由:∵E是AB的中点,F是BC的中点,∴ AC.同理, C.∴EF//HG,EF=HG.∴四边形EFGH是平行四边形.
(2)①AC=BD 由(1),知四边形;EFGH是平行四边形,又∵AC,∴当AC=BD时,FG=HG.∴四边形EFGH是菱形; ②当AC⊥BD时,四边形EFGH是矩形.
21.(1)∵四边形ABCD是矩形,∴∠A=∠D=90°.∵四边形EFGH是菱形,∴HG=EH.
∵AH=2,DG=2,∴DG=AH.,在Rt△DHG和Rt△ABH中,∴Rt△DHG≌Rt△AEH,∴∠DHG=∠AEH.∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°.∴四边形EFGH是正方形.
(2)过点F作FQ⊥CD,交DC的延长线于点Q,连接GE.∴∠Q=90°.∴∠A=∠Q.
∵四边形ABCD是矩形,∴AB//CD.∴∠AEG=∠QGE,即∠AEH+∠HEG=∠QGF+∠FGE.∵四边形EFGH是菱形,∴HE=GF,HE//GF.∴∠HEG=∠FGE,∴∠AEH=∠QGF.
在△AEH和△QGF中,∴△AEH≌△QGF.∴AH=QF=2.
∵DG=6,CD=8,∴CG=2.∴△FCG的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
