2021-2022学年湖南省邵阳市邵东县九年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年湖南省邵阳市邵东县九年级(上)期末数学试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 301.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 21:57:34 | ||
图片预览



文档简介
2021-2022学年湖南省邵阳市邵东县九年级(上)期末数学试卷
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案序号填写在答题卡上。
1.(3分)方程x2=x的根是( )
A.x=0 B.x=±1 C.x1=0,x2=1 D.x1=0,x2=﹣1
2.(3分)在△ABC中,∠C=90°,已知tanA,则cosA=( )
A. B. C. D.
3.(3分)若反比例函数y的图象位于第二、四象限,则k的取值可以是( )
A.0 B.1 C.2 D.3
4.(3分)用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
5.(3分)为了保障人民群众的身体健康,在预防“非典”期间,有关部门加强了对市场的监管力度.在对某商店检查中,抽检了5包口罩(每包10只),5包口罩中合格的口罩的只数分别是:9,10,9,10,10,则估计该商店出售的这批口罩的合格率约为( )
A.95% B.96% C.97% D.98%
6.(3分)如图,DE∥BC,则下列比例式错误的是( )
A. B. C. D.
7.(3分)如图,小正方形的边长均为1,格点△ABC,其顶点均在小正方形的顶点处,则sinC=( )
A. B. C. D.
8.(3分)已知点A(x1,y1),B(x2,y2)是反比例函数y(k>0)图象上的两点,若x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
9.(3分)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
10.(3分)邵东是全国八大箱包生产基地之一.某箱包厂2019年产值3500万元,2021年增加到5300万元.设平均每年增长率为x,则下面所列方程正确的是( )
A.3500(1+x)=5300 B.5300(1+x)=3500
C.5300(1+x)2=3500 D.3500(1+x)2=5300
二、填空题(共8小题,每小题3分,满分24分)
11.(3分)若方程x2﹣2x﹣m=0有两个相等的实数根,则m= .
12.(3分)已知反比例函数y的图象经过点P(a﹣1,2),则a= .
13.(3分)若tan(α﹣15°),则锐角α的度数是 .
14.(3分)如图,已知AC、BD相交于点O,若补充一个条件后,便可得到△AOB∽△DOC,则要补充的条件可以是 .
15.(3分)如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为 .
16.(3分)一般认为,如果一个人的上半身(肚脐以上的高度)与下半身(肚脐以下的高度)符合黄金分割,则这个人好看.某位参加空姐选拔的选手身高160厘米,上半身长65厘米,那么她应穿 cm的鞋子才能好看?(精确到1cm).
17.(3分)如图,点A是反比例函数y的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y的图象于点C,则△OAC的面积为 .
18.(3分)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
三、解答题(共8个小题,满分66分)
19.(8分)计算:﹣12﹣2sin60°+tan45°.
20.(8分)小宏同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款10元的学生一共8人.
(1)小宏同学这次调查的学生共有 人;
(2)这组数据的众数是 元,中位数是 元;
(3)若该校有4000名学生,都进行了捐款,估计全校学生共捐款多少元?
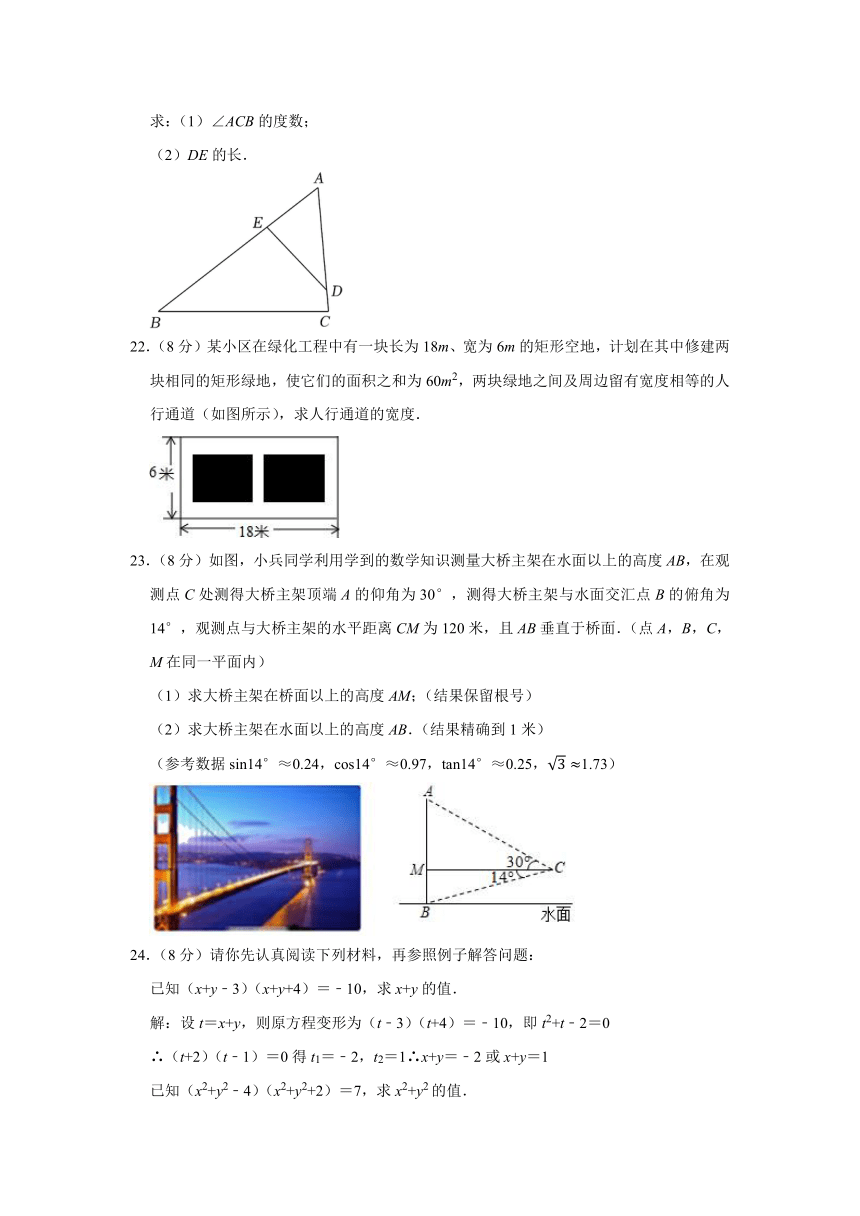
21.(8分)已知:如图,在△ABC中,点D、E分别在边AB、AC上,∠ADE=∠B,AB=2AD,BC=6cm,∠A=58°,∠ADE=40°.
求:(1)∠ACB的度数;
(2)DE的长.
22.(8分)某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
23.(8分)如图,小兵同学利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为120米,且AB垂直于桥面.(点A,B,C,M在同一平面内)
(1)求大桥主架在桥面以上的高度AM;(结果保留根号)
(2)求大桥主架在水面以上的高度AB.(结果精确到1米)
(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,1.73)
24.(8分)请你先认真阅读下列材料,再参照例子解答问题:
已知(x+y﹣3)(x+y+4)=﹣10,求x+y的值.
解:设t=x+y,则原方程变形为(t﹣3)(t+4)=﹣10,即t2+t﹣2=0
∴(t+2)(t﹣1)=0得t1=﹣2,t2=1∴x+y=﹣2或x+y=1
已知(x2+y2﹣4)(x2+y2+2)=7,求x2+y2的值.
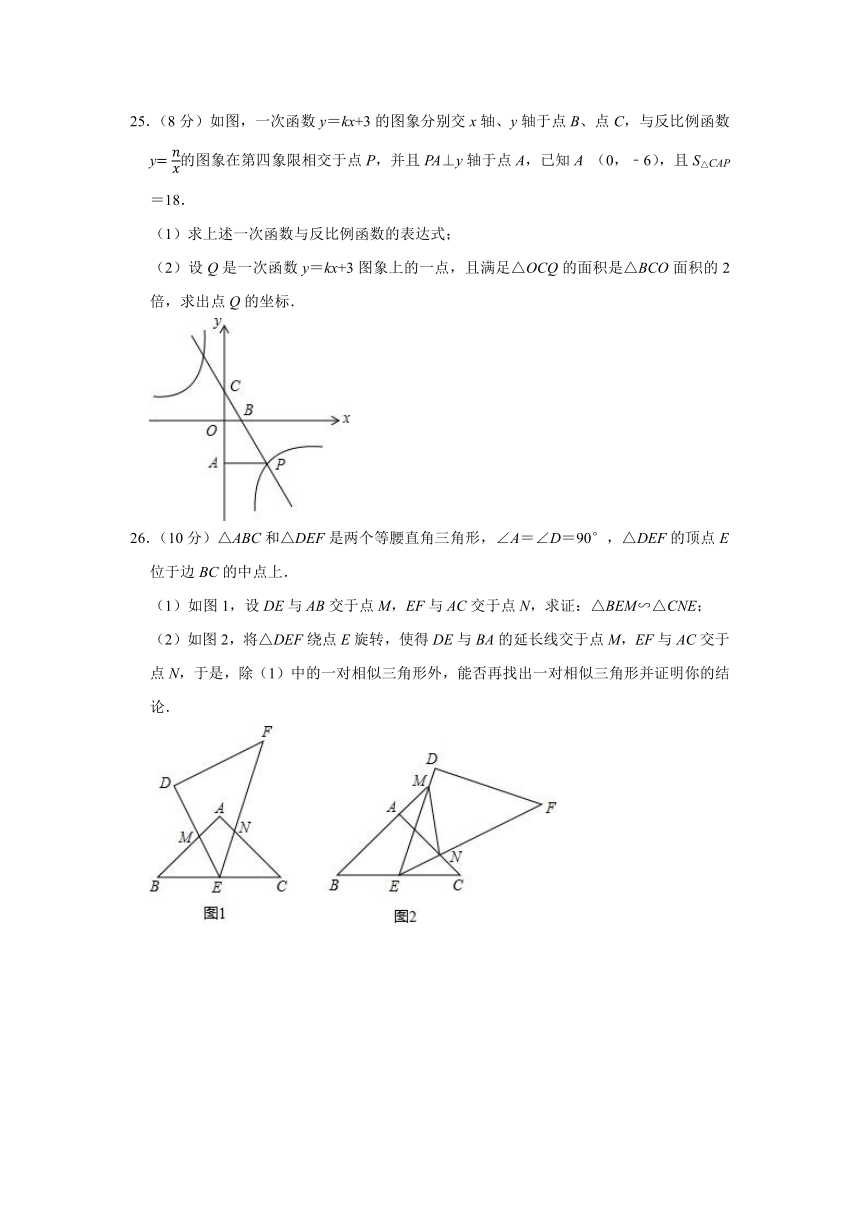
25.(8分)如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y的图象在第四象限相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
26.(10分)△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
参考答案
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案序号填写在答题卡上。
1.(3分)方程x2=x的根是( )
A.x=0 B.x=±1 C.x1=0,x2=1 D.x1=0,x2=﹣1
【分析】利用提公因式法将方程的左边因式分解后求解可得.
【解答】解:∵x2=x,
∴x2﹣x=0,
则x(x﹣1)=0,
∴x=0或x﹣1=0,
解得x1=0,x2=1,
故选:C.
2.(3分)在△ABC中,∠C=90°,已知tanA,则cosA=( )
A. B. C. D.
【分析】在△ABC中,∠C=90°,tanA,设参数,利用勾股定理表示斜边AB,再根据锐角三角函数的意义求解即可.
【解答】解:在△ABC中,∠C=90°,
∵tanA,
∴,
设BC=3k,则AC=4k,
∴AB5k,
∴cosA,
故选:B.
3.(3分)若反比例函数y的图象位于第二、四象限,则k的取值可以是( )
A.0 B.1 C.2 D.3
【分析】反比例函数y的图象位于第二、四象限,比例系数k﹣1<0,即k<1,根据k的取值范围进行选择.
【解答】解:∵反比例函数y的图象位于第二、四象限,
∴k﹣1<0,
即k<1.
故选:A.
4.(3分)用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
【分析】方程移项变形后,利用完全平方公式化简得到结果,即可做出判断.
【解答】解:方程移项得:x2﹣6x=10,
配方得:x2﹣6x+9=19,即(x﹣3)2=19,
故选:D.
5.(3分)为了保障人民群众的身体健康,在预防“非典”期间,有关部门加强了对市场的监管力度.在对某商店检查中,抽检了5包口罩(每包10只),5包口罩中合格的口罩的只数分别是:9,10,9,10,10,则估计该商店出售的这批口罩的合格率约为( )
A.95% B.96% C.97% D.98%
【分析】在本题中,可用样本平均数来估计总体平均数,即求出抽检的5包口罩中的合格率即可.
【解答】解:抽检了5包口罩的平均合格率为100%=96%,则可估计该商店出售的这批口罩的合格率约为96%.
故选:B.
6.(3分)如图,DE∥BC,则下列比例式错误的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理写出相应的比例式,即可得出答案.
【解答】解:∵DE∥BC,
∴,,;
∴A错误;
故选:A.
7.(3分)如图,小正方形的边长均为1,格点△ABC,其顶点均在小正方形的顶点处,则sinC=( )
A. B. C. D.
【分析】连接格点B、D.先说明△CBD是直角三角形,再利用勾股定理计算BD、BC的长,最后求出∠C的正弦值.
【解答】解:连接格点B、D.
∵AD、BD都是小正方形的对角线,
∴∠ADB=2×45°=90°,BD.
∵CB,
∴sinC.
故选:B.
8.(3分)已知点A(x1,y1),B(x2,y2)是反比例函数y(k>0)图象上的两点,若x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
【分析】根据反比例函数的增减性再结合反比例函数图象上点的坐标特征解答即可.
【解答】解:∵k>0,函数图象在一三象限;
若x1<0<x2.说明A在第三象限,B在第一象限.
第一象限的y值总比第三象限的点的y值大,∴y1<0<y2.
故选:A.
9.(3分)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
【分析】根据位似变换的性质计算,得到答案.
【解答】解:∵以原点O为位似中心,相似比为,把△EFO缩小,点E(﹣4,2),
∴点E的对应点E′的坐标是(﹣4,2)或(﹣4×(),2×()),即(﹣2,1)或(2,﹣1),
故选:D.
10.(3分)邵东是全国八大箱包生产基地之一.某箱包厂2019年产值3500万元,2021年增加到5300万元.设平均每年增长率为x,则下面所列方程正确的是( )
A.3500(1+x)=5300 B.5300(1+x)=3500
C.5300(1+x)2=3500 D.3500(1+x)2=5300
【分析】利用该箱包厂2021年的产值=该箱包厂2019年的产值×(1+平均每年增长率)2,即可得出关于x的一元二次方程,此题得解.
【解答】解:依题意得:3500(1+x)2=5300.
故选:D.
二、填空题(共8小题,每小题3分,满分24分)
11.(3分)若方程x2﹣2x﹣m=0有两个相等的实数根,则m= ﹣1 .
【分析】根据方程有两个相等的实数根得出Δ=0,求出m的值即可.
【解答】解:∵方程x2﹣2x﹣m=0有两个相等的实数根,
∴Δ=(﹣2)2﹣4×1×(﹣m)=0,
解得:m=﹣1,
故答案为:﹣1.
12.(3分)已知反比例函数y的图象经过点P(a﹣1,2),则a= ﹣3 .
【分析】根据反比例函数图象上点的坐标特征得到(a﹣1) 2=﹣8,然后解方程即可.
【解答】解:根据题意得(a﹣1) 2=﹣8,
解得a=﹣3.
故答案为﹣3.
13.(3分)若tan(α﹣15°),则锐角α的度数是 75° .
【分析】直接利用特殊角的三角函数值计算得出答案.
【解答】解:∵tan(α﹣15°),
∴α﹣15°=60°,
∴α=75°.
故答案为:75°.
14.(3分)如图,已知AC、BD相交于点O,若补充一个条件后,便可得到△AOB∽△DOC,则要补充的条件可以是 ∠A=∠D(答案不唯一) .
【分析】要使两个三角形相似,满足对应角相等即可.
【解答】解:补充条件∠A=∠D即可;
∵∠AOB=∠COD(对顶角),∠A=∠D,
∴△AOB∽△DOC,
故答案为:∠A=∠D(答案不唯一).
15.(3分)如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为 9m .
【分析】先证明△OCD∽△OAB,则根据相似三角形的性质得到比例式,然后利用比例的性质求AB即可.
【解答】解:∵CD∥AB,
∴△OCD∽△OAB,
∴,即,
∴AB=9,
即旗杆AB的高为9m.
故答案为:9m.
16.(3分)一般认为,如果一个人的上半身(肚脐以上的高度)与下半身(肚脐以下的高度)符合黄金分割,则这个人好看.某位参加空姐选拔的选手身高160厘米,上半身长65厘米,那么她应穿 10 cm的鞋子才能好看?(精确到1cm).
【分析】设某位参加空姐选拔的选手应穿xcm的鞋子,根据黄金分割的定义列出方程,解方程即可.
【解答】解:设某位参加空姐选拔的选手应穿xcm的鞋子,
根据题意,得:,
解得:x≈10.18,
经检验,x≈10.18是原方程的解,
即某位参加空姐选拔的选手应穿10cm的鞋子才能好看.
故答案为:10.
17.(3分)如图,点A是反比例函数y的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y的图象于点C,则△OAC的面积为 2 .
【分析】由于AB⊥x轴,根据反比例函数k的几何意义得到S△AOB=3,S△COB=1,然后利用S△AOC=S△AOB﹣S△COB进行计算.
【解答】解:∵AB⊥x轴,
∴S△AOB|6|=3,S△COB|2|=1,
∴S△AOC=S△AOB﹣S△COB=2.
故答案为:2.
18.(3分)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
【分析】作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
【解答】解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CDx,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=30(1),
答:这段河的宽约为30(1)米.
故答案为:30(1).
三、解答题(共8个小题,满分66分)
19.(8分)计算:﹣12﹣2sin60°+tan45°.
【分析】把特殊角的三角函数值代入进行计算即可.
【解答】解:﹣12﹣2sin60°+tan45°
=﹣1﹣21
=﹣11
.
20.(8分)小宏同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款10元的学生一共8人.
(1)小宏同学这次调查的学生共有 60 人;
(2)这组数据的众数是 20 元,中位数是 20 元;
(3)若该校有4000名学生,都进行了捐款,估计全校学生共捐款多少元?
【分析】(1)求出捐款为10元所占的百分比,根据频率进行计算即可;
(2)根据中位数、众数的定义进行解答即可;
(3)求出平均每人捐款数,即可求出4000人的捐款总数.
【解答】解:(1)860(人),
故答案为:60;
(2)捐款金额出现次数最多的是20元,因此众数是20元,将这60人的捐款数从小到大排列,处在中间位置的两个数都是20元,因此中位数是20元,
故答案为:20,20;
(3)4000=76000(元),
答:该校4000名学生共捐款约76000元.
21.(8分)已知:如图,在△ABC中,点D、E分别在边AB、AC上,∠ADE=∠B,AB=2AD,BC=6cm,∠A=58°,∠ADE=40°.
求:(1)∠ACB的度数;
(2)DE的长.
【分析】(1)利用三角形的内角和定理先求出∠AED的度数,然后再根据两角相等的两个三角形相似证明△ADE∽△ABC即可即可解答;
(2)利用(1)的结论可得相似三角形的对应边成比例即可解答.
【解答】解:(1)在△AED中,
∵∠A=58°,∠ADE=40°,
∴∠AED=180°﹣∠A﹣∠ADE=82°,
∵∠ADE=∠B,∠A=∠A,
∴△ADE∽△ABC,
∴∠ACB=∠AED=82°;
(2)由(1)得:△ADE∽△ABC,
∴,
∵AB=2AD,
∴,
∴DE=3cm.
22.(8分)某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
【分析】设人行道的宽度为x米,根据矩形绿地的面积之和为60米2,列出一元二次方程.
【解答】解:设人行道的宽度为x米,根据题意得,
(18﹣3x)(6﹣2x)=60,
化简整理得,(x﹣1)(x﹣8)=0.
解得x1=1,x2=8(不合题意,舍去).
答:人行通道的宽度是1m.
23.(8分)如图,小兵同学利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为120米,且AB垂直于桥面.(点A,B,C,M在同一平面内)
(1)求大桥主架在桥面以上的高度AM;(结果保留根号)
(2)求大桥主架在水面以上的高度AB.(结果精确到1米)
(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,1.73)
【分析】(1)在Rt△AMC中,利用锐角三角函数的定义即可解答;
(2)在Rt△BMC中,利用锐角三角函数的定义先求出BM,然后再加上AM即可.
【解答】解:(1)由题意得:
∠AMC=∠BMC=90°,
在Rt△AMC中,∠ACM=30°,CM=120米,
∴AM=CM tan∠ACM=12040(米),
答:大桥主架在桥面以上的高度AM为40米;
(2)在Rt△BMC中,CM=120,∠BCM=14°,
∴MB=CM tan∠BCM≈120×0.25=30(米),
∴AB=AM+MB=30+4099(米),
答:大桥主架在水面以上的高度AB为99米.
24.(8分)请你先认真阅读下列材料,再参照例子解答问题:
已知(x+y﹣3)(x+y+4)=﹣10,求x+y的值.
解:设t=x+y,则原方程变形为(t﹣3)(t+4)=﹣10,即t2+t﹣2=0
∴(t+2)(t﹣1)=0得t1=﹣2,t2=1∴x+y=﹣2或x+y=1
已知(x2+y2﹣4)(x2+y2+2)=7,求x2+y2的值.
【分析】根据举例进行解答即可.
【解答】解:设t=x2+y2>0
∴(t﹣4)(t+2)=7
t2﹣2t﹣15=0,
解得:t1=5,t2=﹣3(舍去)
∴x2+y2=5.
25.(8分)如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y的图象在第四象限相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
【分析】(1)由一次函数表达式可得出点C的坐标,结合A点坐标以及三角形的面积公式可得出AP的长度,从而得出点P的坐标,由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式;
(2)设点Q的坐标为(m,m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
【解答】解:(1)令一次函数y=kx+3中的x=0,则y=3,
即点C的坐标为(0,3),
∴AC=3﹣(﹣6)=9.
∵S△CAPAC AP=18,
∴AP=4,
∵点A的坐标为(0,﹣6),
∴点P的坐标为(4,﹣6).
∵点P在一次函数y=kx+3的图象上,
∴﹣6=4k+3,解得:k;
∵点P在反比例函数y的图象上,
∴﹣6,解得:n=﹣24.
∴一次函数的表达式为yx+3,反比例函数的表达式为y.
(2)令一次函数yx+3中的y=0,则0x+3,
解得:x,
即点B的坐标为(,0).
设点Q的坐标为(m,m+3).
∵△OCQ的面积是△BCO面积的2倍,
∴|m|=2,解得:m=±,
∴点Q的坐标为(,9)或(,﹣3).
26.(10分)△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
【分析】因为此题是特殊的三角形,所以首先要分析等腰直角三角形的性质:可得锐角为45°,根据角之间的关系,利用如果两个三角形的三组对应边的比相等,那么这两个三角形相似可判定三角形相似;再根据性质得到比例线段,有夹角相等证得△ECN∽△MEN.
【解答】证明:(1)∵△ABC是等腰直角三角形,
∴∠MBE=45°,∴∠BME+∠MEB=135°
又∵△DEF是等腰直角三角形,∴∠DEF=45°
∴∠NEC+∠MEB=135°
∴∠BME=∠NEC,(4分)
而∠B=∠C=45°,
∴△BEM∽△CNE.(6分)
(2)与(1)同理△BEM∽△CNE,
∴.(8分)
又∵BE=EC,
∴,(10分)
则△ECN与△MEN中有,
又∠ECN=∠MEN=45°,
∴△ECN∽△MEN.(12分)
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案序号填写在答题卡上。
1.(3分)方程x2=x的根是( )
A.x=0 B.x=±1 C.x1=0,x2=1 D.x1=0,x2=﹣1
2.(3分)在△ABC中,∠C=90°,已知tanA,则cosA=( )
A. B. C. D.
3.(3分)若反比例函数y的图象位于第二、四象限,则k的取值可以是( )
A.0 B.1 C.2 D.3
4.(3分)用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
5.(3分)为了保障人民群众的身体健康,在预防“非典”期间,有关部门加强了对市场的监管力度.在对某商店检查中,抽检了5包口罩(每包10只),5包口罩中合格的口罩的只数分别是:9,10,9,10,10,则估计该商店出售的这批口罩的合格率约为( )
A.95% B.96% C.97% D.98%
6.(3分)如图,DE∥BC,则下列比例式错误的是( )
A. B. C. D.
7.(3分)如图,小正方形的边长均为1,格点△ABC,其顶点均在小正方形的顶点处,则sinC=( )
A. B. C. D.
8.(3分)已知点A(x1,y1),B(x2,y2)是反比例函数y(k>0)图象上的两点,若x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
9.(3分)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
10.(3分)邵东是全国八大箱包生产基地之一.某箱包厂2019年产值3500万元,2021年增加到5300万元.设平均每年增长率为x,则下面所列方程正确的是( )
A.3500(1+x)=5300 B.5300(1+x)=3500
C.5300(1+x)2=3500 D.3500(1+x)2=5300
二、填空题(共8小题,每小题3分,满分24分)
11.(3分)若方程x2﹣2x﹣m=0有两个相等的实数根,则m= .
12.(3分)已知反比例函数y的图象经过点P(a﹣1,2),则a= .
13.(3分)若tan(α﹣15°),则锐角α的度数是 .
14.(3分)如图,已知AC、BD相交于点O,若补充一个条件后,便可得到△AOB∽△DOC,则要补充的条件可以是 .
15.(3分)如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为 .
16.(3分)一般认为,如果一个人的上半身(肚脐以上的高度)与下半身(肚脐以下的高度)符合黄金分割,则这个人好看.某位参加空姐选拔的选手身高160厘米,上半身长65厘米,那么她应穿 cm的鞋子才能好看?(精确到1cm).
17.(3分)如图,点A是反比例函数y的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y的图象于点C,则△OAC的面积为 .
18.(3分)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
三、解答题(共8个小题,满分66分)
19.(8分)计算:﹣12﹣2sin60°+tan45°.
20.(8分)小宏同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款10元的学生一共8人.
(1)小宏同学这次调查的学生共有 人;
(2)这组数据的众数是 元,中位数是 元;
(3)若该校有4000名学生,都进行了捐款,估计全校学生共捐款多少元?
21.(8分)已知:如图,在△ABC中,点D、E分别在边AB、AC上,∠ADE=∠B,AB=2AD,BC=6cm,∠A=58°,∠ADE=40°.
求:(1)∠ACB的度数;
(2)DE的长.
22.(8分)某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
23.(8分)如图,小兵同学利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为120米,且AB垂直于桥面.(点A,B,C,M在同一平面内)
(1)求大桥主架在桥面以上的高度AM;(结果保留根号)
(2)求大桥主架在水面以上的高度AB.(结果精确到1米)
(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,1.73)
24.(8分)请你先认真阅读下列材料,再参照例子解答问题:
已知(x+y﹣3)(x+y+4)=﹣10,求x+y的值.
解:设t=x+y,则原方程变形为(t﹣3)(t+4)=﹣10,即t2+t﹣2=0
∴(t+2)(t﹣1)=0得t1=﹣2,t2=1∴x+y=﹣2或x+y=1
已知(x2+y2﹣4)(x2+y2+2)=7,求x2+y2的值.
25.(8分)如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y的图象在第四象限相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
26.(10分)△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
参考答案
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案序号填写在答题卡上。
1.(3分)方程x2=x的根是( )
A.x=0 B.x=±1 C.x1=0,x2=1 D.x1=0,x2=﹣1
【分析】利用提公因式法将方程的左边因式分解后求解可得.
【解答】解:∵x2=x,
∴x2﹣x=0,
则x(x﹣1)=0,
∴x=0或x﹣1=0,
解得x1=0,x2=1,
故选:C.
2.(3分)在△ABC中,∠C=90°,已知tanA,则cosA=( )
A. B. C. D.
【分析】在△ABC中,∠C=90°,tanA,设参数,利用勾股定理表示斜边AB,再根据锐角三角函数的意义求解即可.
【解答】解:在△ABC中,∠C=90°,
∵tanA,
∴,
设BC=3k,则AC=4k,
∴AB5k,
∴cosA,
故选:B.
3.(3分)若反比例函数y的图象位于第二、四象限,则k的取值可以是( )
A.0 B.1 C.2 D.3
【分析】反比例函数y的图象位于第二、四象限,比例系数k﹣1<0,即k<1,根据k的取值范围进行选择.
【解答】解:∵反比例函数y的图象位于第二、四象限,
∴k﹣1<0,
即k<1.
故选:A.
4.(3分)用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )
A.(x+3)2=1 B.(x﹣3)2=1 C.(x+3)2=19 D.(x﹣3)2=19
【分析】方程移项变形后,利用完全平方公式化简得到结果,即可做出判断.
【解答】解:方程移项得:x2﹣6x=10,
配方得:x2﹣6x+9=19,即(x﹣3)2=19,
故选:D.
5.(3分)为了保障人民群众的身体健康,在预防“非典”期间,有关部门加强了对市场的监管力度.在对某商店检查中,抽检了5包口罩(每包10只),5包口罩中合格的口罩的只数分别是:9,10,9,10,10,则估计该商店出售的这批口罩的合格率约为( )
A.95% B.96% C.97% D.98%
【分析】在本题中,可用样本平均数来估计总体平均数,即求出抽检的5包口罩中的合格率即可.
【解答】解:抽检了5包口罩的平均合格率为100%=96%,则可估计该商店出售的这批口罩的合格率约为96%.
故选:B.
6.(3分)如图,DE∥BC,则下列比例式错误的是( )
A. B. C. D.
【分析】根据平行线分线段成比例定理写出相应的比例式,即可得出答案.
【解答】解:∵DE∥BC,
∴,,;
∴A错误;
故选:A.
7.(3分)如图,小正方形的边长均为1,格点△ABC,其顶点均在小正方形的顶点处,则sinC=( )
A. B. C. D.
【分析】连接格点B、D.先说明△CBD是直角三角形,再利用勾股定理计算BD、BC的长,最后求出∠C的正弦值.
【解答】解:连接格点B、D.
∵AD、BD都是小正方形的对角线,
∴∠ADB=2×45°=90°,BD.
∵CB,
∴sinC.
故选:B.
8.(3分)已知点A(x1,y1),B(x2,y2)是反比例函数y(k>0)图象上的两点,若x1<0<x2,则有( )
A.y1<0<y2 B.y2<0<y1 C.y1<y2<0 D.y2<y1<0
【分析】根据反比例函数的增减性再结合反比例函数图象上点的坐标特征解答即可.
【解答】解:∵k>0,函数图象在一三象限;
若x1<0<x2.说明A在第三象限,B在第一象限.
第一象限的y值总比第三象限的点的y值大,∴y1<0<y2.
故选:A.
9.(3分)在平面直角坐标系中,已知点E(﹣4,2),F(﹣3,﹣3),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
【分析】根据位似变换的性质计算,得到答案.
【解答】解:∵以原点O为位似中心,相似比为,把△EFO缩小,点E(﹣4,2),
∴点E的对应点E′的坐标是(﹣4,2)或(﹣4×(),2×()),即(﹣2,1)或(2,﹣1),
故选:D.
10.(3分)邵东是全国八大箱包生产基地之一.某箱包厂2019年产值3500万元,2021年增加到5300万元.设平均每年增长率为x,则下面所列方程正确的是( )
A.3500(1+x)=5300 B.5300(1+x)=3500
C.5300(1+x)2=3500 D.3500(1+x)2=5300
【分析】利用该箱包厂2021年的产值=该箱包厂2019年的产值×(1+平均每年增长率)2,即可得出关于x的一元二次方程,此题得解.
【解答】解:依题意得:3500(1+x)2=5300.
故选:D.
二、填空题(共8小题,每小题3分,满分24分)
11.(3分)若方程x2﹣2x﹣m=0有两个相等的实数根,则m= ﹣1 .
【分析】根据方程有两个相等的实数根得出Δ=0,求出m的值即可.
【解答】解:∵方程x2﹣2x﹣m=0有两个相等的实数根,
∴Δ=(﹣2)2﹣4×1×(﹣m)=0,
解得:m=﹣1,
故答案为:﹣1.
12.(3分)已知反比例函数y的图象经过点P(a﹣1,2),则a= ﹣3 .
【分析】根据反比例函数图象上点的坐标特征得到(a﹣1) 2=﹣8,然后解方程即可.
【解答】解:根据题意得(a﹣1) 2=﹣8,
解得a=﹣3.
故答案为﹣3.
13.(3分)若tan(α﹣15°),则锐角α的度数是 75° .
【分析】直接利用特殊角的三角函数值计算得出答案.
【解答】解:∵tan(α﹣15°),
∴α﹣15°=60°,
∴α=75°.
故答案为:75°.
14.(3分)如图,已知AC、BD相交于点O,若补充一个条件后,便可得到△AOB∽△DOC,则要补充的条件可以是 ∠A=∠D(答案不唯一) .
【分析】要使两个三角形相似,满足对应角相等即可.
【解答】解:补充条件∠A=∠D即可;
∵∠AOB=∠COD(对顶角),∠A=∠D,
∴△AOB∽△DOC,
故答案为:∠A=∠D(答案不唯一).
15.(3分)如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为 9m .
【分析】先证明△OCD∽△OAB,则根据相似三角形的性质得到比例式,然后利用比例的性质求AB即可.
【解答】解:∵CD∥AB,
∴△OCD∽△OAB,
∴,即,
∴AB=9,
即旗杆AB的高为9m.
故答案为:9m.
16.(3分)一般认为,如果一个人的上半身(肚脐以上的高度)与下半身(肚脐以下的高度)符合黄金分割,则这个人好看.某位参加空姐选拔的选手身高160厘米,上半身长65厘米,那么她应穿 10 cm的鞋子才能好看?(精确到1cm).
【分析】设某位参加空姐选拔的选手应穿xcm的鞋子,根据黄金分割的定义列出方程,解方程即可.
【解答】解:设某位参加空姐选拔的选手应穿xcm的鞋子,
根据题意,得:,
解得:x≈10.18,
经检验,x≈10.18是原方程的解,
即某位参加空姐选拔的选手应穿10cm的鞋子才能好看.
故答案为:10.
17.(3分)如图,点A是反比例函数y的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y的图象于点C,则△OAC的面积为 2 .
【分析】由于AB⊥x轴,根据反比例函数k的几何意义得到S△AOB=3,S△COB=1,然后利用S△AOC=S△AOB﹣S△COB进行计算.
【解答】解:∵AB⊥x轴,
∴S△AOB|6|=3,S△COB|2|=1,
∴S△AOC=S△AOB﹣S△COB=2.
故答案为:2.
18.(3分)如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向(点A、B、C在同一平面),则这段河的宽度为 米(结果保留根号)
【分析】作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.
【解答】解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CDx,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x=30(1),
答:这段河的宽约为30(1)米.
故答案为:30(1).
三、解答题(共8个小题,满分66分)
19.(8分)计算:﹣12﹣2sin60°+tan45°.
【分析】把特殊角的三角函数值代入进行计算即可.
【解答】解:﹣12﹣2sin60°+tan45°
=﹣1﹣21
=﹣11
.
20.(8分)小宏同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款10元的学生一共8人.
(1)小宏同学这次调查的学生共有 60 人;
(2)这组数据的众数是 20 元,中位数是 20 元;
(3)若该校有4000名学生,都进行了捐款,估计全校学生共捐款多少元?
【分析】(1)求出捐款为10元所占的百分比,根据频率进行计算即可;
(2)根据中位数、众数的定义进行解答即可;
(3)求出平均每人捐款数,即可求出4000人的捐款总数.
【解答】解:(1)860(人),
故答案为:60;
(2)捐款金额出现次数最多的是20元,因此众数是20元,将这60人的捐款数从小到大排列,处在中间位置的两个数都是20元,因此中位数是20元,
故答案为:20,20;
(3)4000=76000(元),
答:该校4000名学生共捐款约76000元.
21.(8分)已知:如图,在△ABC中,点D、E分别在边AB、AC上,∠ADE=∠B,AB=2AD,BC=6cm,∠A=58°,∠ADE=40°.
求:(1)∠ACB的度数;
(2)DE的长.
【分析】(1)利用三角形的内角和定理先求出∠AED的度数,然后再根据两角相等的两个三角形相似证明△ADE∽△ABC即可即可解答;
(2)利用(1)的结论可得相似三角形的对应边成比例即可解答.
【解答】解:(1)在△AED中,
∵∠A=58°,∠ADE=40°,
∴∠AED=180°﹣∠A﹣∠ADE=82°,
∵∠ADE=∠B,∠A=∠A,
∴△ADE∽△ABC,
∴∠ACB=∠AED=82°;
(2)由(1)得:△ADE∽△ABC,
∴,
∵AB=2AD,
∴,
∴DE=3cm.
22.(8分)某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
【分析】设人行道的宽度为x米,根据矩形绿地的面积之和为60米2,列出一元二次方程.
【解答】解:设人行道的宽度为x米,根据题意得,
(18﹣3x)(6﹣2x)=60,
化简整理得,(x﹣1)(x﹣8)=0.
解得x1=1,x2=8(不合题意,舍去).
答:人行通道的宽度是1m.
23.(8分)如图,小兵同学利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为120米,且AB垂直于桥面.(点A,B,C,M在同一平面内)
(1)求大桥主架在桥面以上的高度AM;(结果保留根号)
(2)求大桥主架在水面以上的高度AB.(结果精确到1米)
(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,1.73)
【分析】(1)在Rt△AMC中,利用锐角三角函数的定义即可解答;
(2)在Rt△BMC中,利用锐角三角函数的定义先求出BM,然后再加上AM即可.
【解答】解:(1)由题意得:
∠AMC=∠BMC=90°,
在Rt△AMC中,∠ACM=30°,CM=120米,
∴AM=CM tan∠ACM=12040(米),
答:大桥主架在桥面以上的高度AM为40米;
(2)在Rt△BMC中,CM=120,∠BCM=14°,
∴MB=CM tan∠BCM≈120×0.25=30(米),
∴AB=AM+MB=30+4099(米),
答:大桥主架在水面以上的高度AB为99米.
24.(8分)请你先认真阅读下列材料,再参照例子解答问题:
已知(x+y﹣3)(x+y+4)=﹣10,求x+y的值.
解:设t=x+y,则原方程变形为(t﹣3)(t+4)=﹣10,即t2+t﹣2=0
∴(t+2)(t﹣1)=0得t1=﹣2,t2=1∴x+y=﹣2或x+y=1
已知(x2+y2﹣4)(x2+y2+2)=7,求x2+y2的值.
【分析】根据举例进行解答即可.
【解答】解:设t=x2+y2>0
∴(t﹣4)(t+2)=7
t2﹣2t﹣15=0,
解得:t1=5,t2=﹣3(舍去)
∴x2+y2=5.
25.(8分)如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y的图象在第四象限相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
【分析】(1)由一次函数表达式可得出点C的坐标,结合A点坐标以及三角形的面积公式可得出AP的长度,从而得出点P的坐标,由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式;
(2)设点Q的坐标为(m,m+3).由一次函数的表达式可找出点B的坐标,结合等底三角形面积的性质可得出关于m的一元一次方程,解方程即可得出m的值,将其代入点Q的坐标中即可.
【解答】解:(1)令一次函数y=kx+3中的x=0,则y=3,
即点C的坐标为(0,3),
∴AC=3﹣(﹣6)=9.
∵S△CAPAC AP=18,
∴AP=4,
∵点A的坐标为(0,﹣6),
∴点P的坐标为(4,﹣6).
∵点P在一次函数y=kx+3的图象上,
∴﹣6=4k+3,解得:k;
∵点P在反比例函数y的图象上,
∴﹣6,解得:n=﹣24.
∴一次函数的表达式为yx+3,反比例函数的表达式为y.
(2)令一次函数yx+3中的y=0,则0x+3,
解得:x,
即点B的坐标为(,0).
设点Q的坐标为(m,m+3).
∵△OCQ的面积是△BCO面积的2倍,
∴|m|=2,解得:m=±,
∴点Q的坐标为(,9)或(,﹣3).
26.(10分)△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
【分析】因为此题是特殊的三角形,所以首先要分析等腰直角三角形的性质:可得锐角为45°,根据角之间的关系,利用如果两个三角形的三组对应边的比相等,那么这两个三角形相似可判定三角形相似;再根据性质得到比例线段,有夹角相等证得△ECN∽△MEN.
【解答】证明:(1)∵△ABC是等腰直角三角形,
∴∠MBE=45°,∴∠BME+∠MEB=135°
又∵△DEF是等腰直角三角形,∴∠DEF=45°
∴∠NEC+∠MEB=135°
∴∠BME=∠NEC,(4分)
而∠B=∠C=45°,
∴△BEM∽△CNE.(6分)
(2)与(1)同理△BEM∽△CNE,
∴.(8分)
又∵BE=EC,
∴,(10分)
则△ECN与△MEN中有,
又∠ECN=∠MEN=45°,
∴△ECN∽△MEN.(12分)
同课章节目录
