北师大版2021-2022年初中数学九年级下册3.8圆内接正多边形同步课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学九年级下册3.8圆内接正多边形同步课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 679.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 21:42:25 | ||
图片预览



文档简介
2021-2022年初中数学九年级下册同步(北师大版)
3.8圆内接正多边形-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.正十边形的中心角是( )
A.18° B.36° C.72° D.144°
2.如图,四边形内接于⊙O ,,那么等于( )
A.110° B.135° C.55° D.125°
3.如图所示,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
4.如果一个正多边形的中心角等于,那么这个多边形的内角和为( )
A. B. C. D.
5.正六边形的边心距为,则该正六边形的外接圆半径为( )
A. B.2 C.3 D.
6.如图,为直径,作的内接正六边形,甲、乙两人的作法分别如下:
甲:1.作的中垂线,交圆于两点;2.作的中垂线,交圆于两点;3.顺次连接六个点,六边形即为所求;
乙:1.以为圆心,长为半径作弧,交圆于两点;2.以为圆心,长为半径作弧,交圆于两点;3.顺次连接六个点,六边形即为所求;
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都不对 D.两人都对
二、填空题
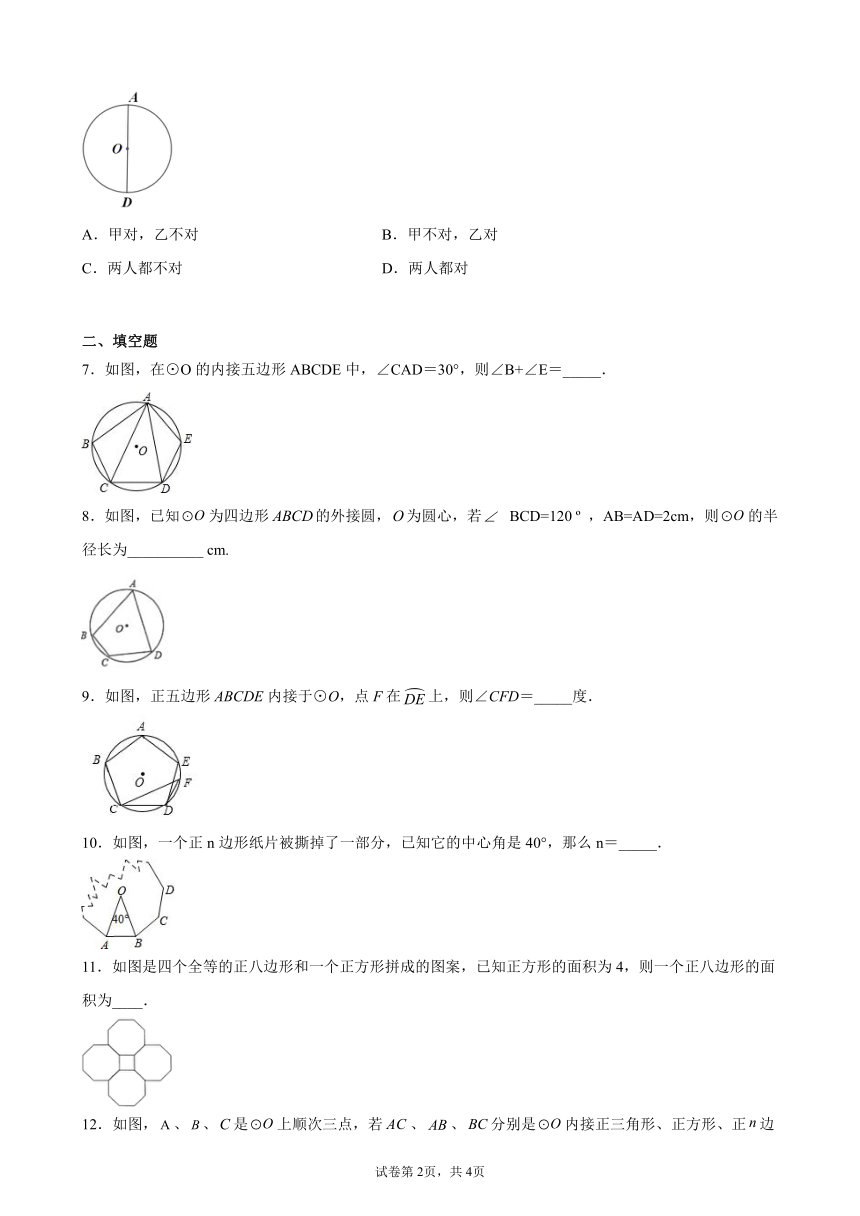
7.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E=_____.
8.如图,已知为四边形的外接圆,为圆心,若 BCD=120 ,AB=AD=2cm,则的半径长为__________ cm.
9.如图,正五边形ABCDE内接于⊙O,点F在上,则∠CFD=_____度.
10.如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=_____.
11.如图是四个全等的正八边形和一个正方形拼成的图案,已知正方形的面积为4,则一个正八边形的面积为____.
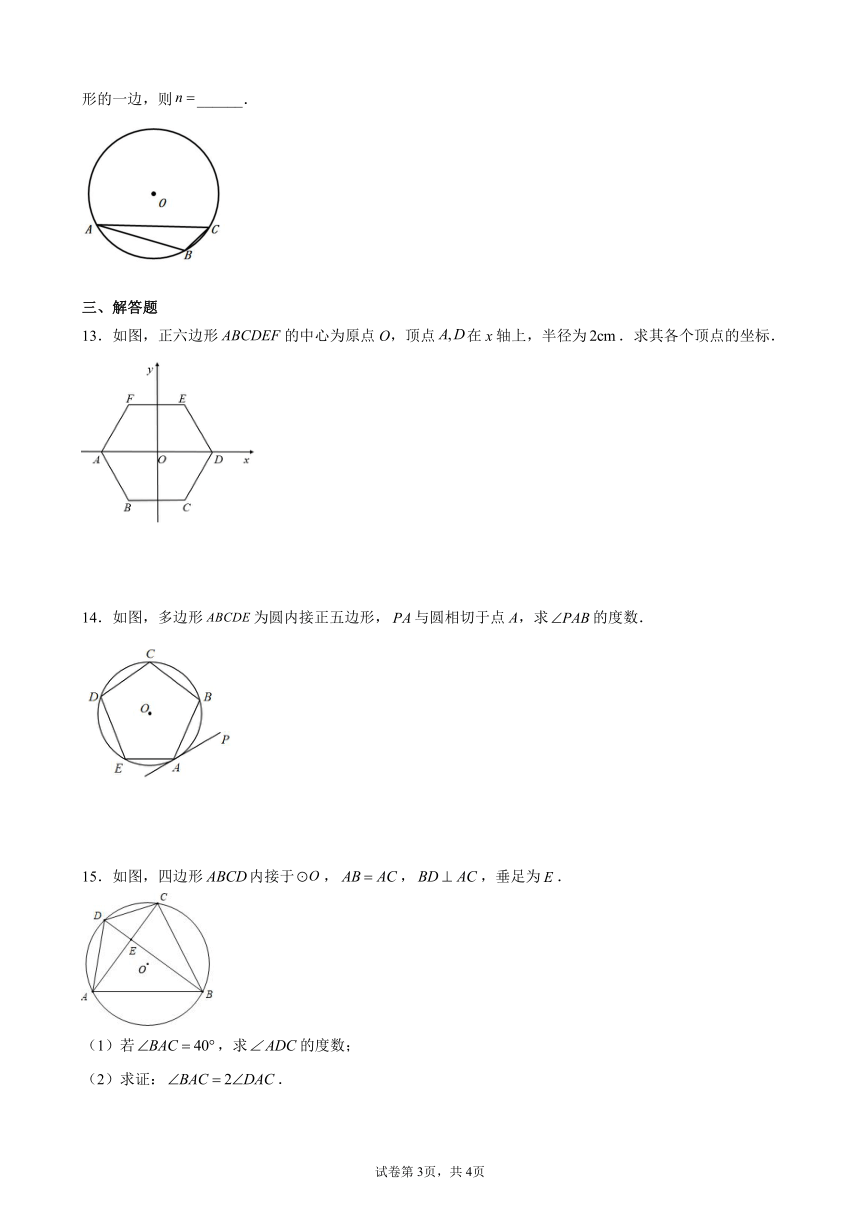
12.如图,、、是上顺次三点,若、、分别是内接正三角形、正方形、正边形的一边,则______.
三、解答题
13.如图,正六边形的中心为原点O,顶点在x轴上,半径为.求其各个顶点的坐标.
14.如图,多边形为圆内接正五边形,与圆相切于点A,求的度数.
15.如图,四边形内接于,,,垂足为.
(1)若,求的度数;
(2)求证:.
16.已知圆的半径为R.
(1)求这个圆的内接正n边形的周长和面积;
(2)利用(1)的结果填写下表:
内接正n边形 正六边形 正十二边形 正二十四边形 …
内接正n边形的周长
内接正n边形的面积
观察上表,随着圆内接正多边形边数的增加,正多边形的周长(面积)有怎样的变化趋势?与圆的周长(面积)进行比较,你能得出什么结论?
17.如图,正六边形ABCDEF在正三角形网格内,点O为正六边形的中心,仅用无刻度的直尺完成以下作图.
(1)在图1中,过点O作AC的平行线;
(2)在图2中,过点E作AC的平行线.
18.已如:⊙O与⊙O上的一点A
(1)求作:⊙O的内接正六边形ABCDEF;( 要求:尺规作图,不写作法但保留作图痕迹)
(2)连接CE,BF,判断四边形BCEF是否为矩形,并说明理由.
参考答案
1.B
【解析】正十边形的每个中心角相等,且其和是360°,故一个中心角的度数为:360°÷10=36°
故选:B
2.D
【解析】解:.
∵四边形内接于⊙O
.
,
故选:D.
3.D
【解析】∵⊙O内切于四边形ABCD,
∴AD+BC=AB+CD,
∵AB=10,BC=7,CD=8,
∴AD+7=10+8,
解得:AD=11.
故选D.
4.B
【解析】解:根据题意可得,这个多边形的边数为:360÷72=5,
∴这个多边形的内角和为:(5-2)×180°=540°.
故选:B.
5.B
【解析】解:如图,
在中,,,
;
故选:.
6.D
【解析】甲:
∵BF是中垂线
∴四边形OCDE是菱形
∴△OCD, △OED都是等边三角形,
同理可得△OAB, △OAF也是等边三角形
∴∠BOC=∠EOF=60°
∴△OBC, △OEF也是等边三角形
∴内接六边形各边相等,各角相等都是120°
∴圆内接六边形ABCDEF是正六边形
乙:
∵AB=AO=BO=AF=OF
∴△OAB, △OAF都是等边三角形,
同理可得△OCD, △OED也是等边三角形
∴∠BOC=∠EOF=60°
∴△OBC, △OEF也是等边三角形
∴内接六边形各边相等,各角相等都是120°
∴圆内接六边形ABCDEF是正六边形
故选D
7.210°.
【解析】解析:连接CE.∵五边形ABCDE是⊙O的内接五边形,∴四边形ABCE是⊙O的内接四边形,∴∠B+∠AEC=180°.∵∠CED=∠CAD=30°,∴∠B+∠E=180°+30°=210°.
故答案为: 210°.
8.
【解析】连接BD,作OE⊥AD,连接OD,
∵⊙O为四边形ABCD的外接圆,∠BCD=120°,
∴∠BAD=60°.
∵AD=AB=2,
∴△ABD是等边三角形.
∴DE=AD=1,∠ODE=∠ADB=30°,
∴OD=.
故答案为.
9.36.
【解析】如图,连接OC,OD.
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CFD=∠COD=36°,
故答案为:36.
10.9
【解析】∵正n边形的中心角==40°,
n==9.
故答案为9.
11.
【解析】解:设正八边形的中心为O,
连接OA,OB,如图所示,
∵正方形的面积为4,
∴AB=2,
∵AB是正八边形的一条边,
∴∠AOB==45°.
过点B作BD⊥OA于点D,设BD=x,则OD=x,OB=OA=x,
∴AD=x-x,
在Rt△ADB中,BD2+AD2=AB2,
即x2+(x-x)2=22,
解得x2=2+,
∴S△AOB=OA BD=×x2=+1,
∴S正八边形=8S△AOB=8×(+1)=8+8,
故答案为:8+8.
12.12
【解析】如图,连接OA、OC、OB.
∵若AC、AB分别是内接正三角形、正方形的一边,
∴,,
∴,
由题意得:,
∴12,
故答案为:12.
13.A(-2,0),B(-1,-),C(1,-),D(2,0),E(1,),F(-1,)
【解析】解:过点E作EG⊥x轴,垂足为G,连接OE,
∵OE=OD,∠EOD=,
∴△OED是正三角形,∠EOG=60°,∠OEG=30°,
∵OE=2cm,∠OGE=90°,
∴OG=OE=1cm,EG===cm,
点E的坐标为(1,),
又由题意知点D的坐标为(2,0),
由图形的对称性可知A(-2,0),B(-1,-),C(1,-),F(-1,).
故这个正六边形ABCDEF各个顶点的坐标分别为A(-2,0),B(-1,-),C(1,-),D(2,0),E(1,),F(-1,).
14.36°
【解析】解:如图, 连接OA、OB,
∵多边形为圆内接正五边形,
∴∠BOA=,
∵OA=OB,
∴∠OAB=∠OBA=,
∵PA为圆O的切线,
∴OA⊥AP,
∴∠OAP=90°,
∴∠PAB=90°-∠OAB=36°.
15.(1);(2)证明见解析
【解析】(1)解:,,
,
四边形是的内接四边形,
,
(2)证明:,
,
,
,
,
,
,
;
16.(1)周长,面积;(2)正六边形、正十二边形和正二十四边形的周长分别6R,24Rsin15°,48Rsin7.5°;面积分别是R2,3R2,12R2sin15°.结论:随着圆内接正多边形边数的增加,正多边形的周长逐渐接近圆的周长2πR,面积逐渐接近圆的面积πR2.
【解析】解:(1)如图,圆的内接正多边形被半径分成n个如图所示的等腰三角形,
其顶角为,即∠AOB=,
作OH⊥AB于点H,作AG⊥OB于点G,则∠AOH=,
∵AO=BO=R,
在Rt△AOH中,sin∠AOH=,即sin=,sin∠AOG=,即sin=,
∴AH=Rsin,AG=R sin,
∴AB=2AH=2Rsin,
正n边形的周长,
面积.
(2)正六边形的周长为6R,面积为R2,
正十二边形的周长=24R sin15°,面积==3R2;
正二十四边形的周长=48Rsin7.5°,面积==12R2sin15°.
故答案为:6R,24Rsin15°,48Rsin7.5°;R2,3R2,12R2sin15°.
结论:随着圆内接正多边形边数的增加,正多边形的周长逐渐接近圆的周长2πR,面积逐渐接近圆的面积πR2.
17.(1)作图见解析;(2)作图见解析.
【解析】(1)如图所示(答案不唯一):
(2)如图所示(答案不唯一):
18.(1)答案见解析;(2)证明见解析.
【解析】解:(1)如图,正六边形ABCDEF为所作;
(2)四边形BCEF为矩形.理由如下:
连接BE,如图,
∵六边形ABCDEF为正六边形,
∴AB=BC=CD=DE=EF=FA,
∴,
∴,
∴,
∴BE为直径,
∴∠BFE=∠BCE=90°,
同理可得∠FBC=∠CEF=90°,
∴四边形BCEF为矩形.
试卷第4页,共4页
试卷第3页,共4页
3.8圆内接正多边形-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.正十边形的中心角是( )
A.18° B.36° C.72° D.144°
2.如图,四边形内接于⊙O ,,那么等于( )
A.110° B.135° C.55° D.125°
3.如图所示,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
4.如果一个正多边形的中心角等于,那么这个多边形的内角和为( )
A. B. C. D.
5.正六边形的边心距为,则该正六边形的外接圆半径为( )
A. B.2 C.3 D.
6.如图,为直径,作的内接正六边形,甲、乙两人的作法分别如下:
甲:1.作的中垂线,交圆于两点;2.作的中垂线,交圆于两点;3.顺次连接六个点,六边形即为所求;
乙:1.以为圆心,长为半径作弧,交圆于两点;2.以为圆心,长为半径作弧,交圆于两点;3.顺次连接六个点,六边形即为所求;
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都不对 D.两人都对
二、填空题
7.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E=_____.
8.如图,已知为四边形的外接圆,为圆心,若 BCD=120 ,AB=AD=2cm,则的半径长为__________ cm.
9.如图,正五边形ABCDE内接于⊙O,点F在上,则∠CFD=_____度.
10.如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=_____.
11.如图是四个全等的正八边形和一个正方形拼成的图案,已知正方形的面积为4,则一个正八边形的面积为____.
12.如图,、、是上顺次三点,若、、分别是内接正三角形、正方形、正边形的一边,则______.
三、解答题
13.如图,正六边形的中心为原点O,顶点在x轴上,半径为.求其各个顶点的坐标.
14.如图,多边形为圆内接正五边形,与圆相切于点A,求的度数.
15.如图,四边形内接于,,,垂足为.
(1)若,求的度数;
(2)求证:.
16.已知圆的半径为R.
(1)求这个圆的内接正n边形的周长和面积;
(2)利用(1)的结果填写下表:
内接正n边形 正六边形 正十二边形 正二十四边形 …
内接正n边形的周长
内接正n边形的面积
观察上表,随着圆内接正多边形边数的增加,正多边形的周长(面积)有怎样的变化趋势?与圆的周长(面积)进行比较,你能得出什么结论?
17.如图,正六边形ABCDEF在正三角形网格内,点O为正六边形的中心,仅用无刻度的直尺完成以下作图.
(1)在图1中,过点O作AC的平行线;
(2)在图2中,过点E作AC的平行线.
18.已如:⊙O与⊙O上的一点A
(1)求作:⊙O的内接正六边形ABCDEF;( 要求:尺规作图,不写作法但保留作图痕迹)
(2)连接CE,BF,判断四边形BCEF是否为矩形,并说明理由.
参考答案
1.B
【解析】正十边形的每个中心角相等,且其和是360°,故一个中心角的度数为:360°÷10=36°
故选:B
2.D
【解析】解:.
∵四边形内接于⊙O
.
,
故选:D.
3.D
【解析】∵⊙O内切于四边形ABCD,
∴AD+BC=AB+CD,
∵AB=10,BC=7,CD=8,
∴AD+7=10+8,
解得:AD=11.
故选D.
4.B
【解析】解:根据题意可得,这个多边形的边数为:360÷72=5,
∴这个多边形的内角和为:(5-2)×180°=540°.
故选:B.
5.B
【解析】解:如图,
在中,,,
;
故选:.
6.D
【解析】甲:
∵BF是中垂线
∴四边形OCDE是菱形
∴△OCD, △OED都是等边三角形,
同理可得△OAB, △OAF也是等边三角形
∴∠BOC=∠EOF=60°
∴△OBC, △OEF也是等边三角形
∴内接六边形各边相等,各角相等都是120°
∴圆内接六边形ABCDEF是正六边形
乙:
∵AB=AO=BO=AF=OF
∴△OAB, △OAF都是等边三角形,
同理可得△OCD, △OED也是等边三角形
∴∠BOC=∠EOF=60°
∴△OBC, △OEF也是等边三角形
∴内接六边形各边相等,各角相等都是120°
∴圆内接六边形ABCDEF是正六边形
故选D
7.210°.
【解析】解析:连接CE.∵五边形ABCDE是⊙O的内接五边形,∴四边形ABCE是⊙O的内接四边形,∴∠B+∠AEC=180°.∵∠CED=∠CAD=30°,∴∠B+∠E=180°+30°=210°.
故答案为: 210°.
8.
【解析】连接BD,作OE⊥AD,连接OD,
∵⊙O为四边形ABCD的外接圆,∠BCD=120°,
∴∠BAD=60°.
∵AD=AB=2,
∴△ABD是等边三角形.
∴DE=AD=1,∠ODE=∠ADB=30°,
∴OD=.
故答案为.
9.36.
【解析】如图,连接OC,OD.
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CFD=∠COD=36°,
故答案为:36.
10.9
【解析】∵正n边形的中心角==40°,
n==9.
故答案为9.
11.
【解析】解:设正八边形的中心为O,
连接OA,OB,如图所示,
∵正方形的面积为4,
∴AB=2,
∵AB是正八边形的一条边,
∴∠AOB==45°.
过点B作BD⊥OA于点D,设BD=x,则OD=x,OB=OA=x,
∴AD=x-x,
在Rt△ADB中,BD2+AD2=AB2,
即x2+(x-x)2=22,
解得x2=2+,
∴S△AOB=OA BD=×x2=+1,
∴S正八边形=8S△AOB=8×(+1)=8+8,
故答案为:8+8.
12.12
【解析】如图,连接OA、OC、OB.
∵若AC、AB分别是内接正三角形、正方形的一边,
∴,,
∴,
由题意得:,
∴12,
故答案为:12.
13.A(-2,0),B(-1,-),C(1,-),D(2,0),E(1,),F(-1,)
【解析】解:过点E作EG⊥x轴,垂足为G,连接OE,
∵OE=OD,∠EOD=,
∴△OED是正三角形,∠EOG=60°,∠OEG=30°,
∵OE=2cm,∠OGE=90°,
∴OG=OE=1cm,EG===cm,
点E的坐标为(1,),
又由题意知点D的坐标为(2,0),
由图形的对称性可知A(-2,0),B(-1,-),C(1,-),F(-1,).
故这个正六边形ABCDEF各个顶点的坐标分别为A(-2,0),B(-1,-),C(1,-),D(2,0),E(1,),F(-1,).
14.36°
【解析】解:如图, 连接OA、OB,
∵多边形为圆内接正五边形,
∴∠BOA=,
∵OA=OB,
∴∠OAB=∠OBA=,
∵PA为圆O的切线,
∴OA⊥AP,
∴∠OAP=90°,
∴∠PAB=90°-∠OAB=36°.
15.(1);(2)证明见解析
【解析】(1)解:,,
,
四边形是的内接四边形,
,
(2)证明:,
,
,
,
,
,
,
;
16.(1)周长,面积;(2)正六边形、正十二边形和正二十四边形的周长分别6R,24Rsin15°,48Rsin7.5°;面积分别是R2,3R2,12R2sin15°.结论:随着圆内接正多边形边数的增加,正多边形的周长逐渐接近圆的周长2πR,面积逐渐接近圆的面积πR2.
【解析】解:(1)如图,圆的内接正多边形被半径分成n个如图所示的等腰三角形,
其顶角为,即∠AOB=,
作OH⊥AB于点H,作AG⊥OB于点G,则∠AOH=,
∵AO=BO=R,
在Rt△AOH中,sin∠AOH=,即sin=,sin∠AOG=,即sin=,
∴AH=Rsin,AG=R sin,
∴AB=2AH=2Rsin,
正n边形的周长,
面积.
(2)正六边形的周长为6R,面积为R2,
正十二边形的周长=24R sin15°,面积==3R2;
正二十四边形的周长=48Rsin7.5°,面积==12R2sin15°.
故答案为:6R,24Rsin15°,48Rsin7.5°;R2,3R2,12R2sin15°.
结论:随着圆内接正多边形边数的增加,正多边形的周长逐渐接近圆的周长2πR,面积逐渐接近圆的面积πR2.
17.(1)作图见解析;(2)作图见解析.
【解析】(1)如图所示(答案不唯一):
(2)如图所示(答案不唯一):
18.(1)答案见解析;(2)证明见解析.
【解析】解:(1)如图,正六边形ABCDEF为所作;
(2)四边形BCEF为矩形.理由如下:
连接BE,如图,
∵六边形ABCDEF为正六边形,
∴AB=BC=CD=DE=EF=FA,
∴,
∴,
∴,
∴BE为直径,
∴∠BFE=∠BCE=90°,
同理可得∠FBC=∠CEF=90°,
∴四边形BCEF为矩形.
试卷第4页,共4页
试卷第3页,共4页
