2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步课堂练习(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步课堂练习(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 330.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 22:28:37 | ||
图片预览




文档简介
2021-2022年初中数学九年级下册同步(北师大版)
2.4二次函数的应用-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
2.如图,在中,,,.动点从点出发,沿边向点以的速度移动(不与点重合),同时动点从点出发,沿边向点以的速度移动(不与点重合).当四边形的面积最小时,经过的时间为( )
A. B. C. D.
3.一台机器原价100万元,若每年的折旧率是x,两年后这台机器约为y万元,则y与x的函数关系式为( )
A. B. C. D.
4.如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是,则该运动员此次掷铅球的成绩是( )
A.6m B.12m C.8m D.10m
5.有一块缺角矩形地皮(如图),其中.现准备用此块地建一座地基为长方形(图中用阴影部分表示)的实验大楼,以下四个方案中,地基面积最大的是( )
A. B. C. D.
6.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
二、填空题
7.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出件,当出售价格是__________元时,才能使利润最大.
8.从地面竖直向上抛出一小球,小球离地面的高度h(米)与小球运动时间t(秒)之间关系是h=30t﹣5t2(0≤t≤6),则小球从抛出后运动4秒共运动的路径长是________米.
9.拱桥呈抛物线形,其函数关系式为,当拱桥下水位线在位置时,水面宽为,这时水面离桥拱顶端的高度是____________________.
10.周长为的矩形铁板上剪去一个等边三角形(这个等边三角形的一边是矩形的宽),则矩形宽为__________时,剩下的面积最大.
11.如图,在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线则电线最低点离地面的距离是_______米.
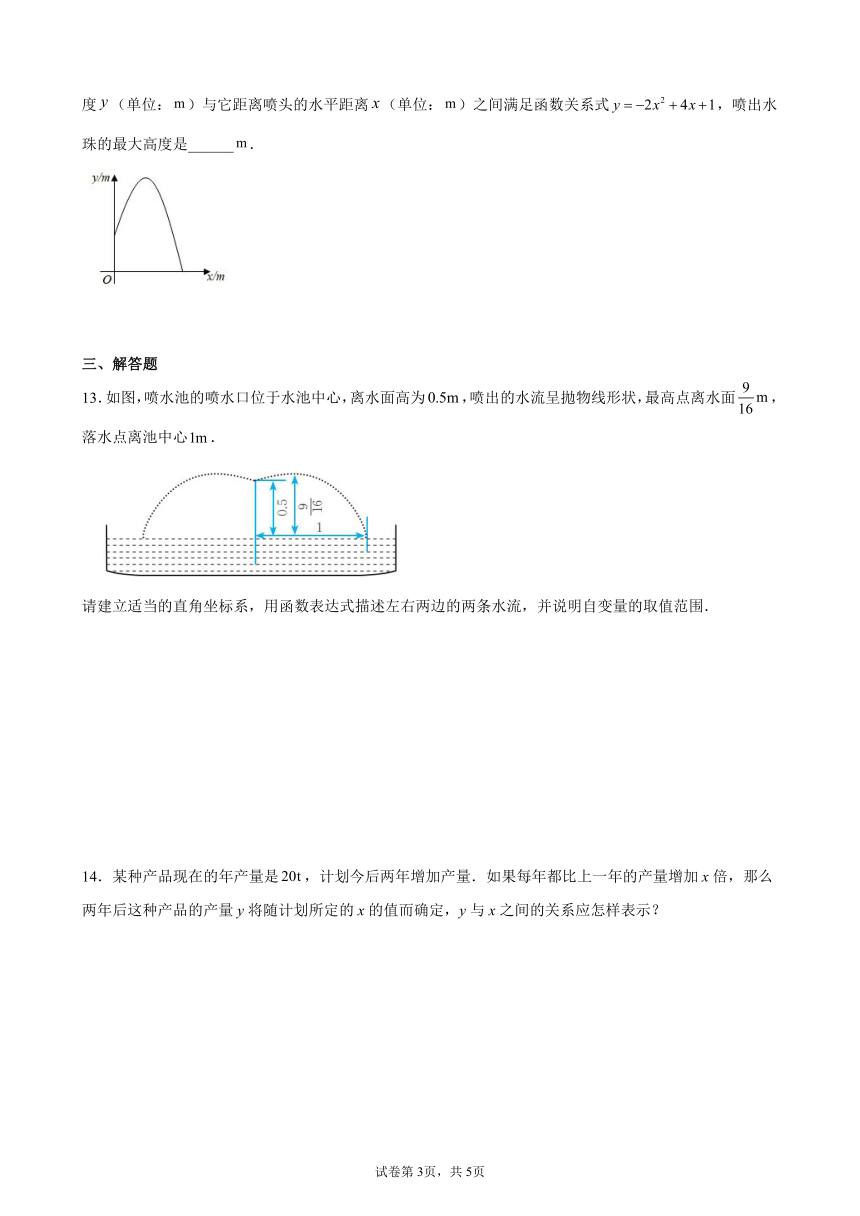
12.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度(单位:)与它距离喷头的水平距离(单位:)之间满足函数关系式,喷出水珠的最大高度是______.
三、解答题
13.如图,喷水池的喷水口位于水池中心,离水面高为,喷出的水流呈拋物线形状,最高点离水面,落水点离池中心.
请建立适当的直角坐标系,用函数表达式描述左右两边的两条水流,并说明自变量的取值范围.
14.某种产品现在的年产量是,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
15.如图(单位:),等腰直角三角形以的速度沿直线l向正方形移动,直到与重合.设时,三角形与正方形重叠部分的面积为.
(1)写出y与x的关系式;
(2)当,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
16.一个人的血压与其年龄及性别有关.对女性来说,正常的收缩压p(毫米汞柱)与年龄x(岁)大致满足关系:;对男性来说,正常的收缩压p(毫米汞柱)与年龄x(岁)大致满足关系:.
(1)利用公式计算你的收缩压;
(2)如果一个女性的收縮压为120毫米汞柱,那么她的年龄大概是多少?
(3)如果一个男性的收缩压为130毫米汞柱,那么他的年龄大概是多少?
17.2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,某市政府加大各部门和各单位的对口扶贫力度.某单位帮扶某村完成一种农产品的销售工作,其成本为每件10元,销售过程中发现,该产品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的一次函数关系.
(1)请求出y与x之间的函数解析式;
(2)该农产品的销售单价为多少元时,每天的销售利润最大?最大利润是多少元?
18.已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.
(1)求抛物线的解析式;
(2)请画出抛物线的图象;
(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
2.B
【解析】解:设运动的时间为x秒(),四边形APQC的面积为y ,
则:,,
∴,
∴,
∴,
∵ ,
∴抛物线开口向上,y有最小值,
∴当时,,y有最小值,,最小值是12,
∴当四边形的面积最小时,经过的时间为2秒.
故选:B.
3.A
【解析】解:由题意得:二年后的价格是为:100×(1-x)×(1-x)=100(1-x)2,
则函数解析式是:y=100(1-x)2.
故选A.
4.D
【解析】解:令=0,
整理得:x2 8x 20=0,
(x 10)(x+2)=0,
解得x1=10,x2= 2(舍去),
故该运动员此次掷铅球的成绩是10m,
故选:D.
5.A
【解析】解:如图,作DG⊥AB于G,EF⊥BC于F,DG,EF交于O,设CN=x,
那么∠EDO=∠EDC-90°=45°,
因此△EOD是等腰直角三角形,同理△EQR,△RPD均为等腰直角三角形,
∴EO=OD=AB-CD=20,RP=DP=CN=x,EQ=QR=AM=EO-RP=20-x,AE=BC-OD=60,
如果设阴影部分MRNB的面积为y,
那么y=MR RN=(AE+QR) (CD+RP)=(80-x)(x+90)=7200-10x-x2
因为y是x的开口向下的抛物线,其对称轴为直线x=-5,
所以当x≥0时,二次函数为减函数,
所以此函数的最大值就是当x=0时,y=7200,
故选:A.
6.B
【解析】解:以拱形桥顶为坐标原点,建立如图直角坐标系xOy,水面宽为AB,与y轴交于E,水面下降后宽度为CD,与y轴交于F,
∵OE=2m,AB=4m,抛物线的对称轴为y轴,
∴点B(2,-2)
设抛物线为y=ax2,
∵抛物线过点B,
∴-2=4a,
∴,
∴抛物线解析式为,
设水面下降nm,
∵CD=AB+,
∴D(),
∵点D在抛物线上,
∴,
解得n=1.
故选择B.
7.65
【解析】解:设最大利润为w元,
则w=(x-30)(100-x)=-(x-65)2+1225,
∵-1<0,0<x<100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
故答案为:65.
8.50
【解析】解:∵h=30t 5t2= 5(t 3)2+45(0≤t≤6),
∴当t=3时,h取得最大值,此时h=45,
∴小球从抛出后运动4秒共运动的路径长是:45+[45 (30×4 5×42)]=50(米),
故答案为50.
9.
【解析】解:函数的顶点为(0,c),对称轴为x=0,
当水面宽为12m时,将x=6代入可得y=c-9,
此时水面离拱桥顶端的高度h是c-(c-9)=9m.
故答案为:9m.
10.
【解析】解:设矩形的宽为xcm,长为,
则剩下的面积=,
∴当时,面积有最大值,
故答案为:.
11.2.8
【解析】解:∵,
∴顶点坐标为,
∴电线最低点离地面的距离是2.8米,
故答 为:2.8.
12.3
【解析】解:∵,
∴当x=1时,,
故答案是:3.
13.图见解析,右边水流的表达式为y=-x2+0.5x+0.5,其中.左边水流的表达式y=-x2-0.5x+0.5,其中
【解析】解:如图,由水池的中心为坐标原点建立平面直角坐标系.
设右边水注的解析式为y=ax2+bx+c,由题意,得
,
解得:.
∴右边水注的解析式为:y=-x2+0.5x+0.5,x的取值范围是:0≤x≤1.
左边的水柱与右边的水柱关于y轴对称,
∴左边水柱的函数表达式为:y=-x2-0.5x+0.5(-1≤x≤0);
14.,y是x的函数
【解析】解:这种产品的原产量是,一年后的产量是,再经过一年后的产量是,即两年后的产量,
即①
①式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
15.(1);(2)8,24.5;(3)当重叠部分的面积是正方形的一半时,三角形移动了5s.
【解析】解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以y=×2x×2x=2x2;
(2)在y=2x2中,
当x=2时,y=8;
当x=3.5时,y=24.5;
(3)在y=2x2中,
因为当y=50时,2x2=50,
所以x2=25,
解得x=5s(负值舍去).
即当重叠部分的面积是正方形的一半时,三角形移动了5s.
16.(1)约为毫米汞柱,答案不唯一;(2)约34岁;(3)约43岁
【解析】解(1)由年龄为30,性别为女性,
所以当时,则
(2) 一个女性的收縮压为120毫米汞柱,
整理得:
,
经检验:不符合题意,取
所以:这位女士的年龄大概是岁.
(3) 一个男性的收缩压为130毫米汞柱,
整理得:
解得:
经检验:不合题意舍去,取
所以这位男士的年龄大概是岁.
17.(1)y=﹣10x+300;(2)销售单价定为20元时,每天销售利润最大,最大销售利润为1000元
【解析】解:(1)设y与x的函数关系式为y=kx+b,将(20,100),(25,50)代入y=kx+b,
得,
解得:,
∴y与x的函数关系式为y=﹣10x+300;
(2)设该款电子产品每天的销售利润为w元,
由题意得w=(x﹣10) y
=(x﹣10)(﹣10x+300)
=﹣10x2+400x﹣3000
=﹣10(x﹣20)2+1000,
∵﹣10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元.
18.(1)二次函数的解析式为:y=x2﹣2x﹣3;(2)见解析;(3)存在,点P的坐标为(1,8)或(1,﹣2)或(1,6)或(1,﹣1)
【解析】解:(1)∵点A(-1,0),C(4,0),
∴AC=5,OC=4,
∵AC=BC=5,
∴B(4,5),
把A(-1,0)和B(4,5)代入二次函数y=x2+bx+c中得:
,解得,
∴二次函数的解析式为:y=x2-2x-3;
(2)由函数的表达式,取值列表如下:
x … -1 0 1 2 3 …
y … 0 -3 -4 -3 0 …
根据表格数据,绘制函数图象如下:
(3)存在,
y=x2-2x-3=(x-1)2-4,
∴设P(1,m),
分三种情况:
①以点B为直角顶点时,由勾股定理得:PB2+AB2=PA2,
∴(4-1)2+(m-5)2+(4+1)2+52=(1+1)2+m2,
解得:m=8,
∴P(1,8);
②以点A为直角顶点时,由勾股定理得:PA2+AB2=PB2,
∴(1+1)2+m2+(4+1)2+52=(4-1)2+(m-5)2,
解得:m=-2,
∴P(1,-2);
③以点P为直角顶点时,由勾股定理得:PB2+PA2=BA2,
∴(1+1)2+m2+(4-1)2+(m-5)2=(4+1)2+52,
解得:m=6或-1,
∴P(1,6)或(1,-1);
综上,点P的坐标为(1,8)或(1,-2)或(1,6)或(1,-1).
答案第1页,共2页
答案第1页,共2页
2.4二次函数的应用-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
2.如图,在中,,,.动点从点出发,沿边向点以的速度移动(不与点重合),同时动点从点出发,沿边向点以的速度移动(不与点重合).当四边形的面积最小时,经过的时间为( )
A. B. C. D.
3.一台机器原价100万元,若每年的折旧率是x,两年后这台机器约为y万元,则y与x的函数关系式为( )
A. B. C. D.
4.如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是,则该运动员此次掷铅球的成绩是( )
A.6m B.12m C.8m D.10m
5.有一块缺角矩形地皮(如图),其中.现准备用此块地建一座地基为长方形(图中用阴影部分表示)的实验大楼,以下四个方案中,地基面积最大的是( )
A. B. C. D.
6.如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
二、填空题
7.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出件,当出售价格是__________元时,才能使利润最大.
8.从地面竖直向上抛出一小球,小球离地面的高度h(米)与小球运动时间t(秒)之间关系是h=30t﹣5t2(0≤t≤6),则小球从抛出后运动4秒共运动的路径长是________米.
9.拱桥呈抛物线形,其函数关系式为,当拱桥下水位线在位置时,水面宽为,这时水面离桥拱顶端的高度是____________________.
10.周长为的矩形铁板上剪去一个等边三角形(这个等边三角形的一边是矩形的宽),则矩形宽为__________时,剩下的面积最大.
11.如图,在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线则电线最低点离地面的距离是_______米.
12.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度(单位:)与它距离喷头的水平距离(单位:)之间满足函数关系式,喷出水珠的最大高度是______.
三、解答题
13.如图,喷水池的喷水口位于水池中心,离水面高为,喷出的水流呈拋物线形状,最高点离水面,落水点离池中心.
请建立适当的直角坐标系,用函数表达式描述左右两边的两条水流,并说明自变量的取值范围.
14.某种产品现在的年产量是,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
15.如图(单位:),等腰直角三角形以的速度沿直线l向正方形移动,直到与重合.设时,三角形与正方形重叠部分的面积为.
(1)写出y与x的关系式;
(2)当,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
16.一个人的血压与其年龄及性别有关.对女性来说,正常的收缩压p(毫米汞柱)与年龄x(岁)大致满足关系:;对男性来说,正常的收缩压p(毫米汞柱)与年龄x(岁)大致满足关系:.
(1)利用公式计算你的收缩压;
(2)如果一个女性的收縮压为120毫米汞柱,那么她的年龄大概是多少?
(3)如果一个男性的收缩压为130毫米汞柱,那么他的年龄大概是多少?
17.2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,某市政府加大各部门和各单位的对口扶贫力度.某单位帮扶某村完成一种农产品的销售工作,其成本为每件10元,销售过程中发现,该产品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的一次函数关系.
(1)请求出y与x之间的函数解析式;
(2)该农产品的销售单价为多少元时,每天的销售利润最大?最大利润是多少元?
18.已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.
(1)求抛物线的解析式;
(2)请画出抛物线的图象;
(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:设小正方形边长为xcm,由题意知:
现在底面长为(20-2x)cm,宽为(10-2x)cm,
则y=(10-2x)(20-2x)(0<x<5),
故选:C.
2.B
【解析】解:设运动的时间为x秒(),四边形APQC的面积为y ,
则:,,
∴,
∴,
∴,
∵ ,
∴抛物线开口向上,y有最小值,
∴当时,,y有最小值,,最小值是12,
∴当四边形的面积最小时,经过的时间为2秒.
故选:B.
3.A
【解析】解:由题意得:二年后的价格是为:100×(1-x)×(1-x)=100(1-x)2,
则函数解析式是:y=100(1-x)2.
故选A.
4.D
【解析】解:令=0,
整理得:x2 8x 20=0,
(x 10)(x+2)=0,
解得x1=10,x2= 2(舍去),
故该运动员此次掷铅球的成绩是10m,
故选:D.
5.A
【解析】解:如图,作DG⊥AB于G,EF⊥BC于F,DG,EF交于O,设CN=x,
那么∠EDO=∠EDC-90°=45°,
因此△EOD是等腰直角三角形,同理△EQR,△RPD均为等腰直角三角形,
∴EO=OD=AB-CD=20,RP=DP=CN=x,EQ=QR=AM=EO-RP=20-x,AE=BC-OD=60,
如果设阴影部分MRNB的面积为y,
那么y=MR RN=(AE+QR) (CD+RP)=(80-x)(x+90)=7200-10x-x2
因为y是x的开口向下的抛物线,其对称轴为直线x=-5,
所以当x≥0时,二次函数为减函数,
所以此函数的最大值就是当x=0时,y=7200,
故选:A.
6.B
【解析】解:以拱形桥顶为坐标原点,建立如图直角坐标系xOy,水面宽为AB,与y轴交于E,水面下降后宽度为CD,与y轴交于F,
∵OE=2m,AB=4m,抛物线的对称轴为y轴,
∴点B(2,-2)
设抛物线为y=ax2,
∵抛物线过点B,
∴-2=4a,
∴,
∴抛物线解析式为,
设水面下降nm,
∵CD=AB+,
∴D(),
∵点D在抛物线上,
∴,
解得n=1.
故选择B.
7.65
【解析】解:设最大利润为w元,
则w=(x-30)(100-x)=-(x-65)2+1225,
∵-1<0,0<x<100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
故答案为:65.
8.50
【解析】解:∵h=30t 5t2= 5(t 3)2+45(0≤t≤6),
∴当t=3时,h取得最大值,此时h=45,
∴小球从抛出后运动4秒共运动的路径长是:45+[45 (30×4 5×42)]=50(米),
故答案为50.
9.
【解析】解:函数的顶点为(0,c),对称轴为x=0,
当水面宽为12m时,将x=6代入可得y=c-9,
此时水面离拱桥顶端的高度h是c-(c-9)=9m.
故答案为:9m.
10.
【解析】解:设矩形的宽为xcm,长为,
则剩下的面积=,
∴当时,面积有最大值,
故答案为:.
11.2.8
【解析】解:∵,
∴顶点坐标为,
∴电线最低点离地面的距离是2.8米,
故答 为:2.8.
12.3
【解析】解:∵,
∴当x=1时,,
故答案是:3.
13.图见解析,右边水流的表达式为y=-x2+0.5x+0.5,其中.左边水流的表达式y=-x2-0.5x+0.5,其中
【解析】解:如图,由水池的中心为坐标原点建立平面直角坐标系.
设右边水注的解析式为y=ax2+bx+c,由题意,得
,
解得:.
∴右边水注的解析式为:y=-x2+0.5x+0.5,x的取值范围是:0≤x≤1.
左边的水柱与右边的水柱关于y轴对称,
∴左边水柱的函数表达式为:y=-x2-0.5x+0.5(-1≤x≤0);
14.,y是x的函数
【解析】解:这种产品的原产量是,一年后的产量是,再经过一年后的产量是,即两年后的产量,
即①
①式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
15.(1);(2)8,24.5;(3)当重叠部分的面积是正方形的一半时,三角形移动了5s.
【解析】解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以y=×2x×2x=2x2;
(2)在y=2x2中,
当x=2时,y=8;
当x=3.5时,y=24.5;
(3)在y=2x2中,
因为当y=50时,2x2=50,
所以x2=25,
解得x=5s(负值舍去).
即当重叠部分的面积是正方形的一半时,三角形移动了5s.
16.(1)约为毫米汞柱,答案不唯一;(2)约34岁;(3)约43岁
【解析】解(1)由年龄为30,性别为女性,
所以当时,则
(2) 一个女性的收縮压为120毫米汞柱,
整理得:
,
经检验:不符合题意,取
所以:这位女士的年龄大概是岁.
(3) 一个男性的收缩压为130毫米汞柱,
整理得:
解得:
经检验:不合题意舍去,取
所以这位男士的年龄大概是岁.
17.(1)y=﹣10x+300;(2)销售单价定为20元时,每天销售利润最大,最大销售利润为1000元
【解析】解:(1)设y与x的函数关系式为y=kx+b,将(20,100),(25,50)代入y=kx+b,
得,
解得:,
∴y与x的函数关系式为y=﹣10x+300;
(2)设该款电子产品每天的销售利润为w元,
由题意得w=(x﹣10) y
=(x﹣10)(﹣10x+300)
=﹣10x2+400x﹣3000
=﹣10(x﹣20)2+1000,
∵﹣10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元.
18.(1)二次函数的解析式为:y=x2﹣2x﹣3;(2)见解析;(3)存在,点P的坐标为(1,8)或(1,﹣2)或(1,6)或(1,﹣1)
【解析】解:(1)∵点A(-1,0),C(4,0),
∴AC=5,OC=4,
∵AC=BC=5,
∴B(4,5),
把A(-1,0)和B(4,5)代入二次函数y=x2+bx+c中得:
,解得,
∴二次函数的解析式为:y=x2-2x-3;
(2)由函数的表达式,取值列表如下:
x … -1 0 1 2 3 …
y … 0 -3 -4 -3 0 …
根据表格数据,绘制函数图象如下:
(3)存在,
y=x2-2x-3=(x-1)2-4,
∴设P(1,m),
分三种情况:
①以点B为直角顶点时,由勾股定理得:PB2+AB2=PA2,
∴(4-1)2+(m-5)2+(4+1)2+52=(1+1)2+m2,
解得:m=8,
∴P(1,8);
②以点A为直角顶点时,由勾股定理得:PA2+AB2=PB2,
∴(1+1)2+m2+(4+1)2+52=(4-1)2+(m-5)2,
解得:m=-2,
∴P(1,-2);
③以点P为直角顶点时,由勾股定理得:PB2+PA2=BA2,
∴(1+1)2+m2+(4-1)2+(m-5)2=(4+1)2+52,
解得:m=6或-1,
∴P(1,6)或(1,-1);
综上,点P的坐标为(1,8)或(1,-2)或(1,6)或(1,-1).
答案第1页,共2页
答案第1页,共2页
