2021-2022学年北师大版九年级数学下册3.2圆的对称性同步课堂练习(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性同步课堂练习(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 467.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 22:35:32 | ||
图片预览



文档简介
2021-2022年初中数学九年级下册同步(北师大版)
3.2圆的对称性-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
2.下列说法中,不正确的是( )
A.圆是轴对称图形
B.圆的任意一条直径所在的直线都是圆的对称轴
C.圆的任意一条直径都是圆的对称轴
D.经过圆心的任意直线都是圆的对称轴
3.下列4个说法中:①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆; 正确的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
5.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①;②HC=BF:③MF=FC:④,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
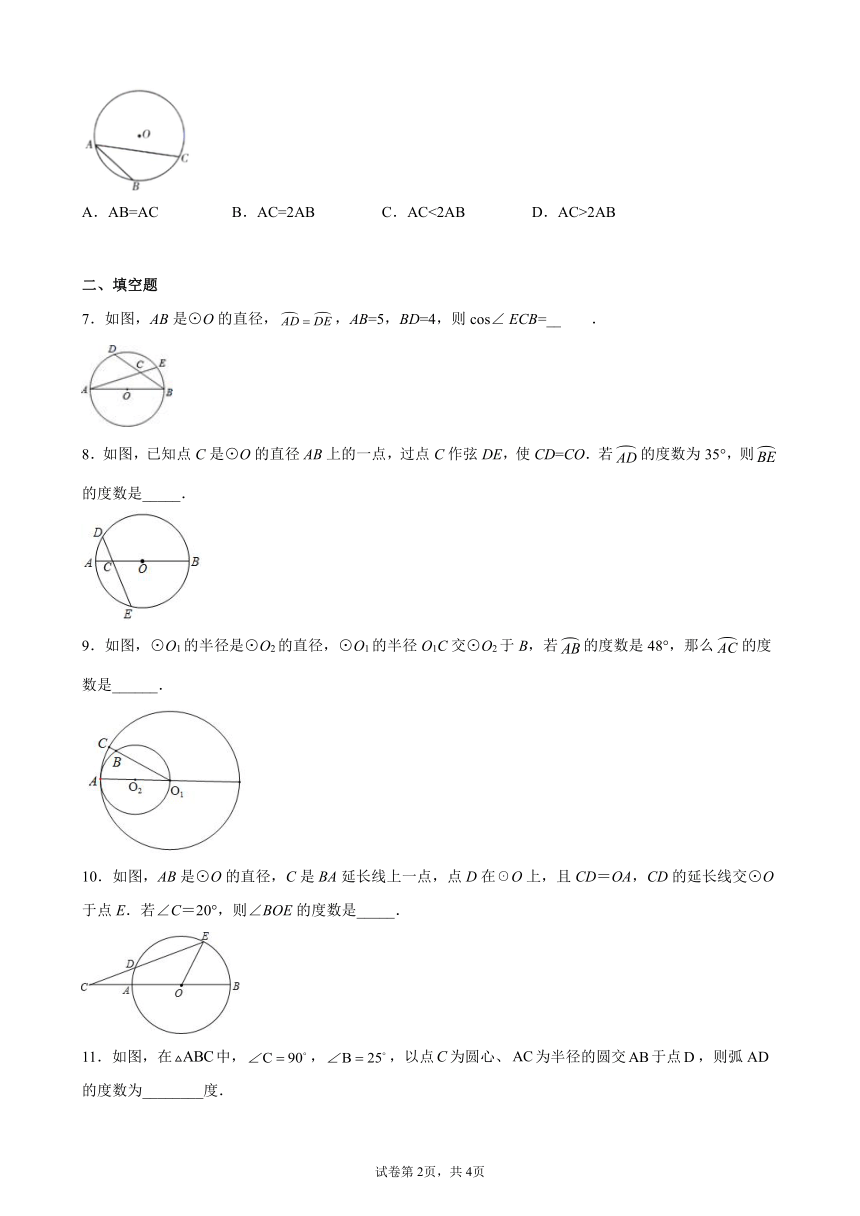
6.如图,在中,,则弦AC与AB的关系是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
二、填空题
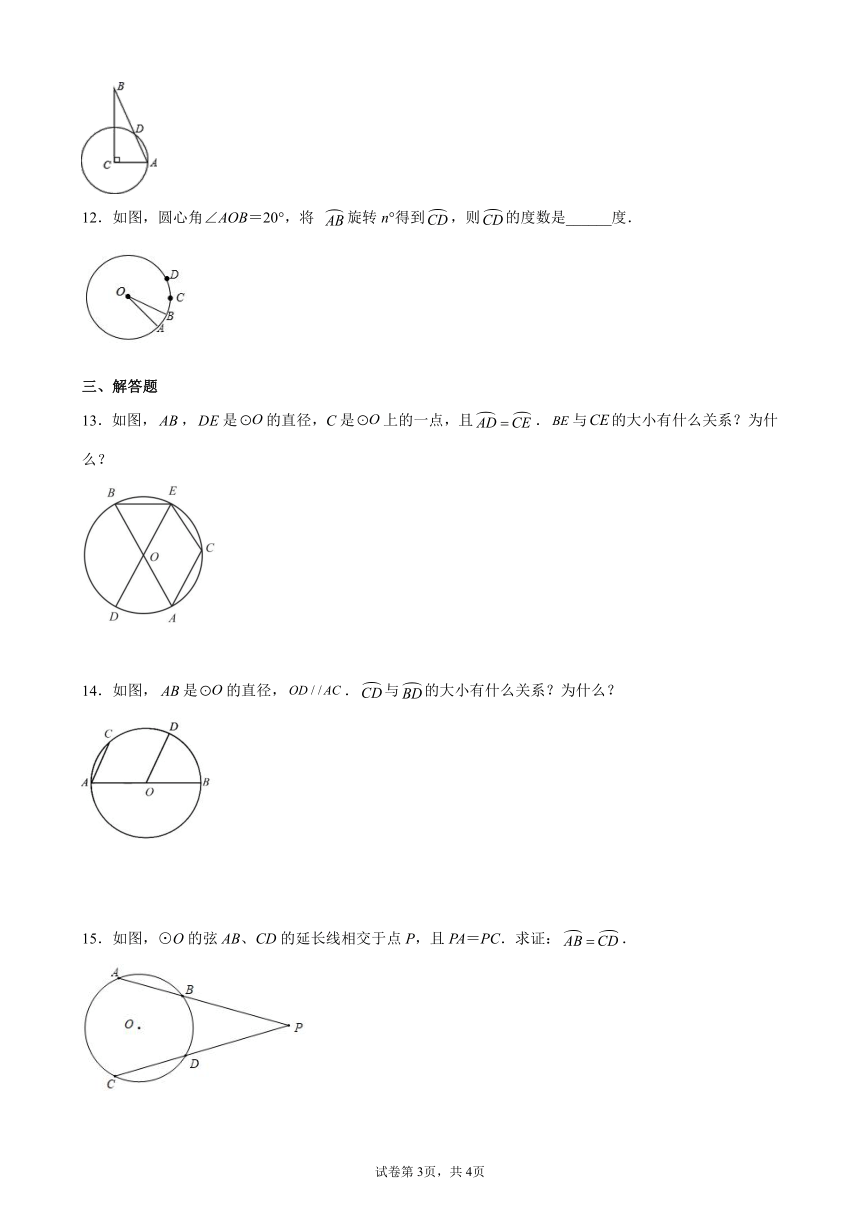
7.如图,AB是⊙O的直径,,AB=5,BD=4,则cos∠ ECB=__.
8.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是_____.
9.如图,⊙O1的半径是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,若的度数是48°,那么的度数是______.
10.如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是_____.
11.如图,在中,,,以点为圆心、为半径的圆交于点,则弧AD的度数为________度.
12.如图,圆心角∠AOB=20°,将 旋转n°得到,则的度数是______度.
三、解答题
13.如图,,是的直径,C是上的一点,且.与的大小有什么关系?为什么?
14.如图,是的直径,.与的大小有什么关系?为什么?
15.如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:.
16.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】A、直径所在的直线为圆的对称轴,所以A错误;
B、经过圆心的直线是圆的对称轴,所以B正确;
C、与圆相交的直线不一定是圆的对称轴,所以C错误;
D、与半径相交的圆心的直线是圆的对称轴,所以D错误.
故选:B.
2.C
【解析】A、圆是轴对称图形,正确;
B、圆的任意一条直径所在得直线都是圆的对称轴,正确;
C、圆的任一直径所在的直线都是圆的对称轴,错误;
D、经过圆心的任意直线都是圆的对称轴,正确,
故选:C.
3.B
【解析】解:①直径是最长的弦,故正确;
②最长的弦才是直径,故错误;
③过圆心的任一直线都是圆的对称轴,故正确;
④半圆是弧,但弧不一定是半圆,故错误,
正确的有两个,
故选B.
4.B
【解析】A中,等弦所对应的弧可以相等也可以互补构成新圆;
B中,等弧所对应的弦相等,故选B
C中,圆心角相等所对应的弦可能互补;
D中,弦相等,圆心角可能互补;
故选B
5.C
【解析】解:∵F为的中点,
∴,故①正确,
∴∠FCM=∠FAC,
∵∠FCG=∠ACM+∠FCM,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴=180°,
∴=180°,
∴,故④正确,
故选:C.
6.C
【解析】解:连接BC
∵,
∴弧AB=弧BC,
∴AB=BC,
∵在△ABC中,AB+BC>AC,
∴AC<2AB.
故选C.
7.
【解析】解:连接AD, BE,
,
∴,
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
∴∠ECB+∠EBC=90°,∠DBA+∠DAB=90°,
∴∠ECB=∠DAB.
AB=5,BD=4 ,
,
∴.
8.105°.
【解析】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
9.24°
【解析】解:如图,连接
的度数是48°,
的度数是
故答案是:
10.60°;
【解析】解:连接OD,
∵CD=OA=OD,∠C=20°,
∴∠ODE=2∠C=40°,
∵OD=OE,
∴∠E=∠EDO=40°,
∴∠EOB=∠C+∠E=40°+20°=60°.
11.
【解析】连接CD.
∵∠ACB=90°,∠B=25°,∴∠A=90°﹣∠B=65°.
∵CA=CD,∴∠A=∠CDA=65°,∴∠ACD=180°﹣2∠A=50°,∴弧AD的度数是50度.
12.20
【解析】解:
∵将旋转n°得到,
∴
∴∠DOC=∠AOB=20°,
∴的度数为20度.
故答案为20.
13.,理由见解析
【解析】解:,理由如下:
∵,
∴.
又∵,
∴.
∴.
14.,理由见解析
【解析】,理由如下,
如图,连接,
,
,
,
,
,
.
15.证明见解析
【解析】证明:连接AC、OA、OB、OC、OD,
∵PA=PC,
∴∠PAC=∠PCA,
∵∠PAC∠BOC,∠PCA∠AOD,
∴∠BOC=∠AOD,
∴,
∴,即.
16.见解析
【解析】证明:∵AB=CD,
∴,
∴,
即,
∴,
∴CE=BE.
答案第1页,共2页
答案第1页,共2页
3.2圆的对称性-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
2.下列说法中,不正确的是( )
A.圆是轴对称图形
B.圆的任意一条直径所在的直线都是圆的对称轴
C.圆的任意一条直径都是圆的对称轴
D.经过圆心的任意直线都是圆的对称轴
3.下列4个说法中:①直径是弦;②弦是直径;③任何一条直径所在的直线都是圆的对称轴;④弧是半圆; 正确的有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
5.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①;②HC=BF:③MF=FC:④,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,在中,,则弦AC与AB的关系是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
二、填空题
7.如图,AB是⊙O的直径,,AB=5,BD=4,则cos∠ ECB=__.
8.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是_____.
9.如图,⊙O1的半径是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,若的度数是48°,那么的度数是______.
10.如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是_____.
11.如图,在中,,,以点为圆心、为半径的圆交于点,则弧AD的度数为________度.
12.如图,圆心角∠AOB=20°,将 旋转n°得到,则的度数是______度.
三、解答题
13.如图,,是的直径,C是上的一点,且.与的大小有什么关系?为什么?
14.如图,是的直径,.与的大小有什么关系?为什么?
15.如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:.
16.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】A、直径所在的直线为圆的对称轴,所以A错误;
B、经过圆心的直线是圆的对称轴,所以B正确;
C、与圆相交的直线不一定是圆的对称轴,所以C错误;
D、与半径相交的圆心的直线是圆的对称轴,所以D错误.
故选:B.
2.C
【解析】A、圆是轴对称图形,正确;
B、圆的任意一条直径所在得直线都是圆的对称轴,正确;
C、圆的任一直径所在的直线都是圆的对称轴,错误;
D、经过圆心的任意直线都是圆的对称轴,正确,
故选:C.
3.B
【解析】解:①直径是最长的弦,故正确;
②最长的弦才是直径,故错误;
③过圆心的任一直线都是圆的对称轴,故正确;
④半圆是弧,但弧不一定是半圆,故错误,
正确的有两个,
故选B.
4.B
【解析】A中,等弦所对应的弧可以相等也可以互补构成新圆;
B中,等弧所对应的弦相等,故选B
C中,圆心角相等所对应的弦可能互补;
D中,弦相等,圆心角可能互补;
故选B
5.C
【解析】解:∵F为的中点,
∴,故①正确,
∴∠FCM=∠FAC,
∵∠FCG=∠ACM+∠FCM,∠AME=∠FMC=∠ACM+∠FAC,
∴∠AME=∠FMC=∠FCG>∠FCM,
∴FC>FM,故③错误,
∵AB⊥CD,FH⊥AC,
∴∠AEM=∠CGF=90°,
∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,
∴∠CFH=∠BAF,
∴,
∴HC=BF,故②正确,
∵∠AGF=90°,
∴∠CAF+∠AFH=90°,
∴=180°,
∴=180°,
∴,故④正确,
故选:C.
6.C
【解析】解:连接BC
∵,
∴弧AB=弧BC,
∴AB=BC,
∵在△ABC中,AB+BC>AC,
∴AC<2AB.
故选C.
7.
【解析】解:连接AD, BE,
,
∴,
∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
∴∠ECB+∠EBC=90°,∠DBA+∠DAB=90°,
∴∠ECB=∠DAB.
AB=5,BD=4 ,
,
∴.
8.105°.
【解析】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
9.24°
【解析】解:如图,连接
的度数是48°,
的度数是
故答案是:
10.60°;
【解析】解:连接OD,
∵CD=OA=OD,∠C=20°,
∴∠ODE=2∠C=40°,
∵OD=OE,
∴∠E=∠EDO=40°,
∴∠EOB=∠C+∠E=40°+20°=60°.
11.
【解析】连接CD.
∵∠ACB=90°,∠B=25°,∴∠A=90°﹣∠B=65°.
∵CA=CD,∴∠A=∠CDA=65°,∴∠ACD=180°﹣2∠A=50°,∴弧AD的度数是50度.
12.20
【解析】解:
∵将旋转n°得到,
∴
∴∠DOC=∠AOB=20°,
∴的度数为20度.
故答案为20.
13.,理由见解析
【解析】解:,理由如下:
∵,
∴.
又∵,
∴.
∴.
14.,理由见解析
【解析】,理由如下,
如图,连接,
,
,
,
,
,
.
15.证明见解析
【解析】证明:连接AC、OA、OB、OC、OD,
∵PA=PC,
∴∠PAC=∠PCA,
∵∠PAC∠BOC,∠PCA∠AOD,
∴∠BOC=∠AOD,
∴,
∴,即.
16.见解析
【解析】证明:∵AB=CD,
∴,
∴,
即,
∴,
∴CE=BE.
答案第1页,共2页
答案第1页,共2页
