2021-2022学年数学九年级下册北师大版3.4圆周角和圆心角的关系 同步课堂练习(word解析版)
文档属性
| 名称 | 2021-2022学年数学九年级下册北师大版3.4圆周角和圆心角的关系 同步课堂练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 525.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 22:27:36 | ||
图片预览



文档简介
2021-2022年初中数学九年级下册同步(北师大版)
3.4圆周角和圆心角的关系 课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各角中,是圆心角的是( )
A. B. C. D.
2.下列四个图形的角是圆周角的是( )
A. B. C. D.
3.如图,是的直径,且,点,在上,,,点是线段的中点,则( )
A.1 B. C.3 D.
4.如图所示,A,D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
A.35° B.55° C.65° D.70°
5.如图,在直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为( )
A.12 B.10 C.14 D.15
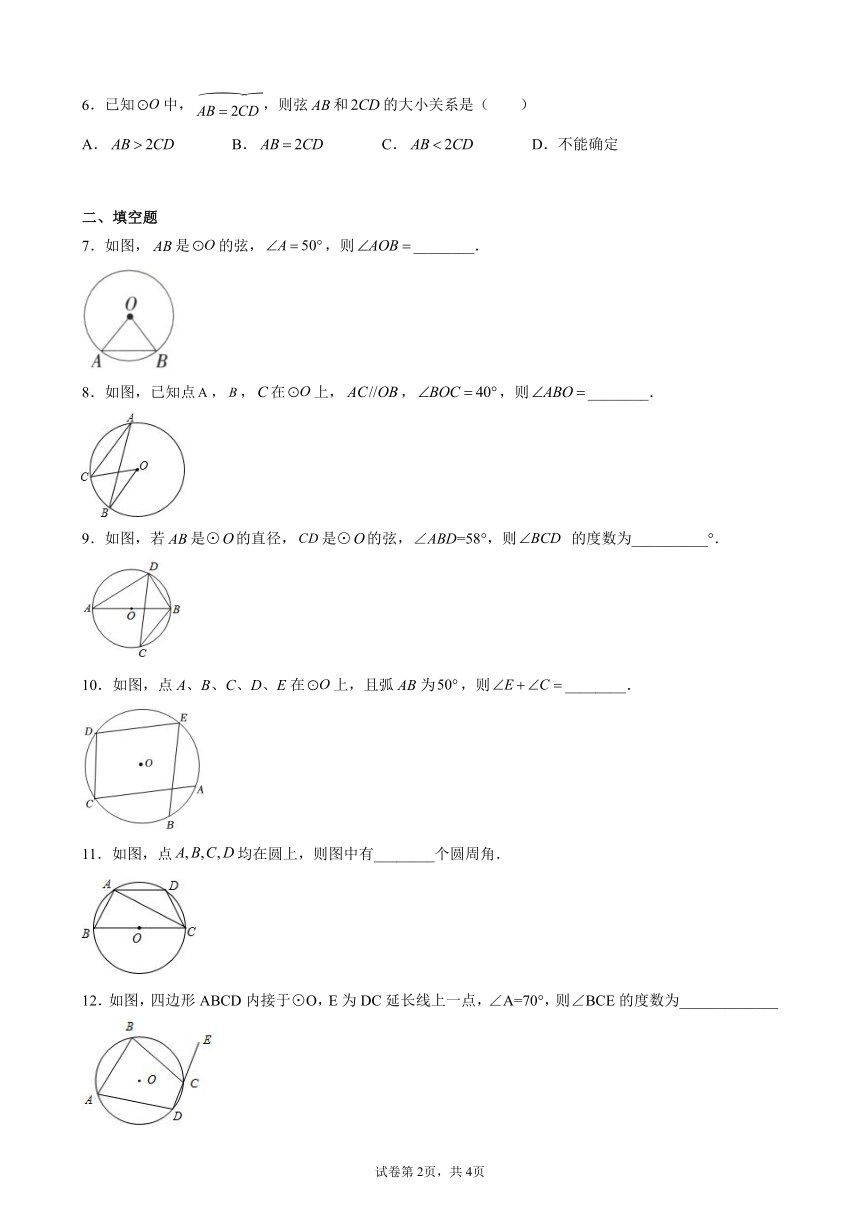
6.已知中,,则弦和的大小关系是( )
A. B. C. D.不能确定
二、填空题
7.如图,是的弦,,则________.
8.如图,已知点,,在上,,,则________.
9.如图,若是⊙的直径,是⊙的弦,∠ABD=58°,则 的度数为__________°.
10.如图,点A、B、C、D、E在上,且弧AB为,则________.
11.如图,点均在圆上,则图中有________个圆周角.
12.如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为_____________
三、解答题
13.如图,的直径,C为上的一点,,求的长.
14.某处靠近海岸的海域有一片暗礁,当地海洋管理部门在海岸上建造了两座灯塔,,通告所有船只不要进入以为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮正向暗礁区域靠近,当多大时,才能避开暗礁?
15.如图,已知AB、CD是⊙O的直径,DF∥AB交⊙O于点F,BE∥DC交⊙O于点E.
(1)求证:BE=DF;
(2)写出图中4组不同的且相等的劣弧(不要求证明).
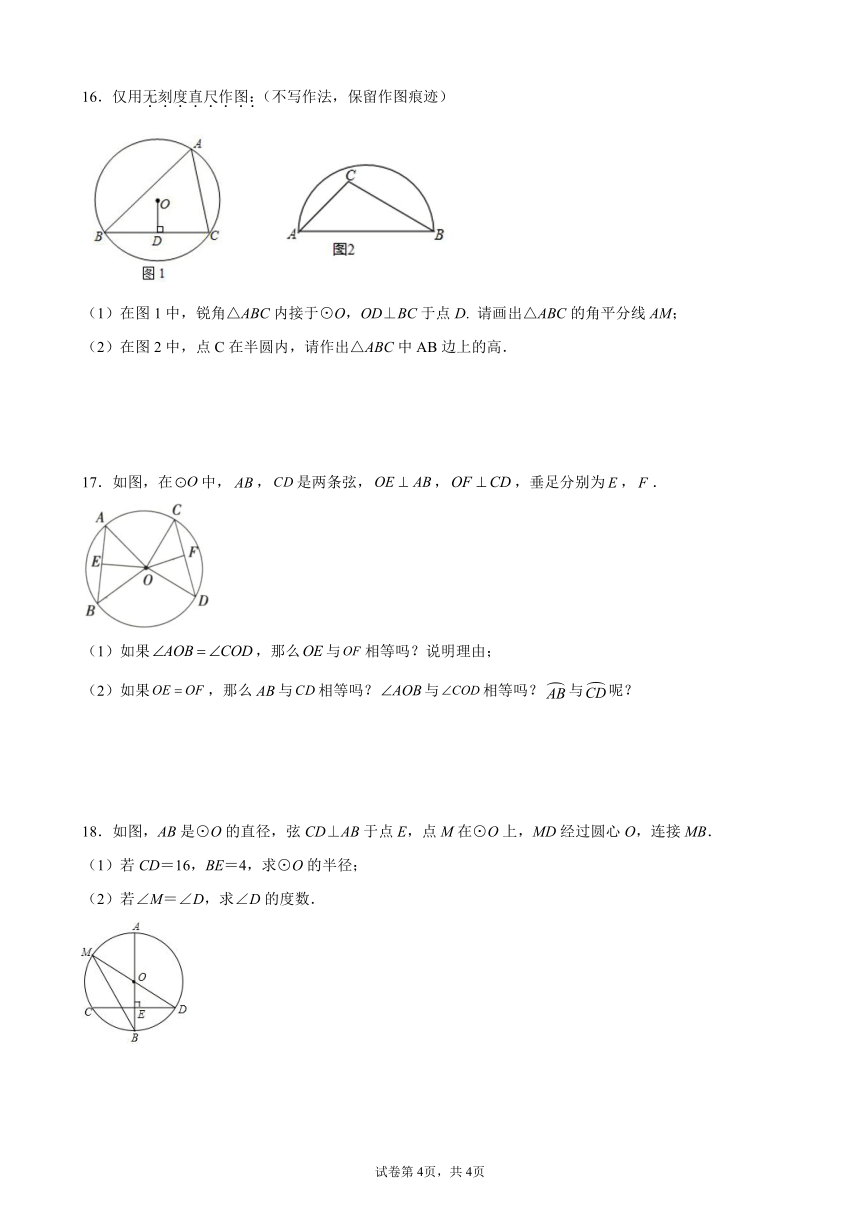
16.仅用无刻度直尺作图:(不写作法,保留作图痕迹)
(1)在图1中,锐角△ABC内接于⊙O,OD⊥BC于点D. 请画出△ABC的角平分线AM;
(2)在图2中,点C在半圆内,请作出△ABC中AB边上的高.
17.如图,在中,,是两条弦,,,垂足分别为,.
(1)如果,那么与相等吗?说明理由;
(2)如果,那么与相等吗?与相等吗?与呢?
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的半径;
(2)若∠M=∠D,求∠D的度数.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】顶点在圆心,两边和圆相交的角是圆心角,选项D中,是圆心角,
故选D.
2.A
【解析】解:A、图中的角是圆周角,故本选项符合题意;
B、图中的角不是圆周角,故本选项不符合题意;
C、图中的角不是圆周角,故本选项不符合题意;
D、图中的角不是圆周角,故本选项不符合题意;
故选:A.
3.B
【解析】∵,,
∴,
∴,
∵,为中点,
∴,,
∵,
∴,
∴,
故选B.
4.B
【解析】解:连接AB,
由同弧所对的圆周角相等得∠ABC=∠D=35°,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ACB=90°-35°=55°.
故选B.
5.B
【解析】如图,连接EF,因为∠EOF=90°,所以EF是直径,
由勾股定理得,EF=10.
故选B.
6.C
【解析】如图,取的中点,则,
∵,
∴,
∴,
∵ ,
∴ .
故选C.
7.
【解析】解:∵,
∴,又,
∴,
故答案为:.
8.
【解析】解:∵,
∴,
∵,
∴.
故答案为:20°
9.
【解析】解:∵AB是⊙O的直径,
∴∠ADB=90°.
∵∠ABD=58°,
∴∠A=90° 58°=32°,
∴∠BCD=∠A=32°.
故答案为:.
10.
【解析】弧的度数等于它所对应的圆心角的度数,由于弧为,所以 ,
顶点在圆上且两边都和圆相交的角叫做圆周角,而一条弧所对的圆周角等于它所对的圆心角的一半,所以:
, ,
,
故答案为:.
11.8
【解析】解:以点为顶点的圆周角各有1个,以点为顶点的圆周角各有3个,共有8个圆周角.
故答案为8.
12.70°
【解析】作辅助线连接BO,DO
∵圆心角是对应圆周角的两倍,
故答案为70°.
13..
【解析】解:是的直径,
,
在 中,
,,
.
14.使∠APB<55°,即在外行驶,就能避开暗礁.
【解析】解:货轮P在航行时,只要使∠APB<55°,即在外行驶,就能避开暗礁.
15.(1)见解析;(2)答案不唯一,图中相等的劣弧有:弧DF=弧BE,弧EC=弧FA,弧AC=弧BD,弧DA=弧BC.
【解析】(1)∵DF∥AB,BE∥DC,
∴∠EBA=∠COA=∠CDF.
∴弧ECA=弧CAF,
∴弧BE=弧DF,
∴BE=DF;
(2) 由(1)可得,弧DF=弧BE;
∵弧ECA=弧CAF,
∴弧EC=弧FA;
∵,
∴弧AC=弧BD;
∵弧BE+弧EC=弧AF+弧DF;
∴弧DA=弧BC.
∴综上所述,图中相等的劣弧有:弧DF=弧BE,弧EC=弧FA,弧AC=弧BD,弧DA=弧BC.
16.(1)见解析; (2)见解析.
【解析】(1)延长OD交⊙O于点E,连接AE交BC于点M,AM即为所求;
(2)延长AC、BC分别交半圆于点E、D,连接BE、AD并延长交于点P,连接PC并延长交AB于点F,则线段CF即为所求的高:
17.(1)相等,见解析;(2),,,见解析
【解析】解:(1)解:OE=OF,
理由是:∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=∠AOB,∠FOD=∠COD,
∵∠AOB=∠COD,
∴∠EOB=∠FOD,
∵在△EOB和△FOD中,
∴△EOB≌△FOD(AAS),
∴OE=OF.;
(2),,.
理由:∵,,
∴,
又∵,,∴,
∴,
∵,,,,
∴,,
∴,∴,.
18.(1)10;(2)
【解析】解:(1),,
,
设,则
又,
,
解得:,
的半径是10.
(2),,
,
,
.
答案第1页,共2页
答案第1页,共2页
3.4圆周角和圆心角的关系 课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各角中,是圆心角的是( )
A. B. C. D.
2.下列四个图形的角是圆周角的是( )
A. B. C. D.
3.如图,是的直径,且,点,在上,,,点是线段的中点,则( )
A.1 B. C.3 D.
4.如图所示,A,D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是( )
A.35° B.55° C.65° D.70°
5.如图,在直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为( )
A.12 B.10 C.14 D.15
6.已知中,,则弦和的大小关系是( )
A. B. C. D.不能确定
二、填空题
7.如图,是的弦,,则________.
8.如图,已知点,,在上,,,则________.
9.如图,若是⊙的直径,是⊙的弦,∠ABD=58°,则 的度数为__________°.
10.如图,点A、B、C、D、E在上,且弧AB为,则________.
11.如图,点均在圆上,则图中有________个圆周角.
12.如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为_____________
三、解答题
13.如图,的直径,C为上的一点,,求的长.
14.某处靠近海岸的海域有一片暗礁,当地海洋管理部门在海岸上建造了两座灯塔,,通告所有船只不要进入以为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮正向暗礁区域靠近,当多大时,才能避开暗礁?
15.如图,已知AB、CD是⊙O的直径,DF∥AB交⊙O于点F,BE∥DC交⊙O于点E.
(1)求证:BE=DF;
(2)写出图中4组不同的且相等的劣弧(不要求证明).
16.仅用无刻度直尺作图:(不写作法,保留作图痕迹)
(1)在图1中,锐角△ABC内接于⊙O,OD⊥BC于点D. 请画出△ABC的角平分线AM;
(2)在图2中,点C在半圆内,请作出△ABC中AB边上的高.
17.如图,在中,,是两条弦,,,垂足分别为,.
(1)如果,那么与相等吗?说明理由;
(2)如果,那么与相等吗?与相等吗?与呢?
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的半径;
(2)若∠M=∠D,求∠D的度数.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】顶点在圆心,两边和圆相交的角是圆心角,选项D中,是圆心角,
故选D.
2.A
【解析】解:A、图中的角是圆周角,故本选项符合题意;
B、图中的角不是圆周角,故本选项不符合题意;
C、图中的角不是圆周角,故本选项不符合题意;
D、图中的角不是圆周角,故本选项不符合题意;
故选:A.
3.B
【解析】∵,,
∴,
∴,
∵,为中点,
∴,,
∵,
∴,
∴,
故选B.
4.B
【解析】解:连接AB,
由同弧所对的圆周角相等得∠ABC=∠D=35°,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ACB=90°-35°=55°.
故选B.
5.B
【解析】如图,连接EF,因为∠EOF=90°,所以EF是直径,
由勾股定理得,EF=10.
故选B.
6.C
【解析】如图,取的中点,则,
∵,
∴,
∴,
∵ ,
∴ .
故选C.
7.
【解析】解:∵,
∴,又,
∴,
故答案为:.
8.
【解析】解:∵,
∴,
∵,
∴.
故答案为:20°
9.
【解析】解:∵AB是⊙O的直径,
∴∠ADB=90°.
∵∠ABD=58°,
∴∠A=90° 58°=32°,
∴∠BCD=∠A=32°.
故答案为:.
10.
【解析】弧的度数等于它所对应的圆心角的度数,由于弧为,所以 ,
顶点在圆上且两边都和圆相交的角叫做圆周角,而一条弧所对的圆周角等于它所对的圆心角的一半,所以:
, ,
,
故答案为:.
11.8
【解析】解:以点为顶点的圆周角各有1个,以点为顶点的圆周角各有3个,共有8个圆周角.
故答案为8.
12.70°
【解析】作辅助线连接BO,DO
∵圆心角是对应圆周角的两倍,
故答案为70°.
13..
【解析】解:是的直径,
,
在 中,
,,
.
14.使∠APB<55°,即在外行驶,就能避开暗礁.
【解析】解:货轮P在航行时,只要使∠APB<55°,即在外行驶,就能避开暗礁.
15.(1)见解析;(2)答案不唯一,图中相等的劣弧有:弧DF=弧BE,弧EC=弧FA,弧AC=弧BD,弧DA=弧BC.
【解析】(1)∵DF∥AB,BE∥DC,
∴∠EBA=∠COA=∠CDF.
∴弧ECA=弧CAF,
∴弧BE=弧DF,
∴BE=DF;
(2) 由(1)可得,弧DF=弧BE;
∵弧ECA=弧CAF,
∴弧EC=弧FA;
∵,
∴弧AC=弧BD;
∵弧BE+弧EC=弧AF+弧DF;
∴弧DA=弧BC.
∴综上所述,图中相等的劣弧有:弧DF=弧BE,弧EC=弧FA,弧AC=弧BD,弧DA=弧BC.
16.(1)见解析; (2)见解析.
【解析】(1)延长OD交⊙O于点E,连接AE交BC于点M,AM即为所求;
(2)延长AC、BC分别交半圆于点E、D,连接BE、AD并延长交于点P,连接PC并延长交AB于点F,则线段CF即为所求的高:
17.(1)相等,见解析;(2),,,见解析
【解析】解:(1)解:OE=OF,
理由是:∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=∠AOB,∠FOD=∠COD,
∵∠AOB=∠COD,
∴∠EOB=∠FOD,
∵在△EOB和△FOD中,
∴△EOB≌△FOD(AAS),
∴OE=OF.;
(2),,.
理由:∵,,
∴,
又∵,,∴,
∴,
∵,,,,
∴,,
∴,∴,.
18.(1)10;(2)
【解析】解:(1),,
,
设,则
又,
,
解得:,
的半径是10.
(2),,
,
,
.
答案第1页,共2页
答案第1页,共2页
