2021-2022学年北师大版九年级数学下册3.3垂径定理同步课堂练习(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理同步课堂练习(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 398.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 22:38:37 | ||
图片预览




文档简介
2021-2022年初中数学九年级下册同步(北师大版)
3.3垂径定理-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,则OM的长为( )
A.9cm B.6cm C.3cm D.cm
2.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1或7 B.7 C.1 D.3或4
3.如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,AB=12cm,AO=8cm,则OC长为( )cm
A.5 B.4 C. D.
4.如图,已知的半径为5,弦,则上到弦所在直线的距离为2的点有( )
A.4个 B.3个 C.2个 D.1个
5.如图,矩形中,,,,分别是,边上的动点,,以为直径的与交于点,.则的最大值为( ).
A.48 B.45 C.42 D.40
6.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2 B.4 C.4 D.2
二、填空题
7.半径为2cm的⊙O中,弦长为2cm的弦所对的圆心角度数为 ____.
8.已知的半径为,弦,且,则弦和之间的距离为_______.
9.如图,在⊙O中,弦的长为4,圆心到弦的距离为2,则的度数为______.
10.如图,是的弦,是的中点,连接并延长交于点.若,则的半径是_________.
11.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径⊥弦时,平分)可以求解.现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.
12.如图,⊙O的半径为6,的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有_____个.
三、解答题
13.的半径为13cm,AB、CD是的两条弦,,AB=24cm,CD=10cm,求AB和CD之间的距离.
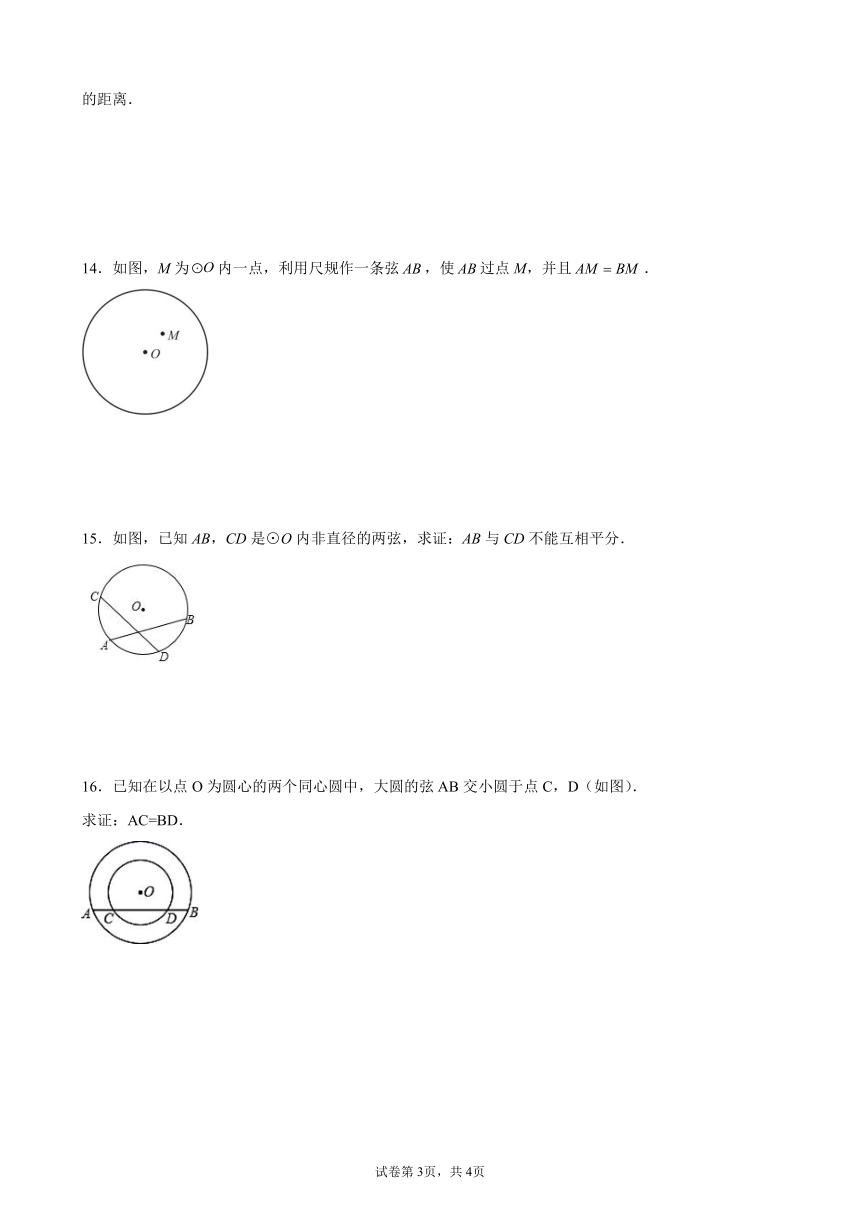
14.如图,M为内一点,利用尺规作一条弦,使过点M,并且.
15.如图,已知AB,CD是⊙O内非直径的两弦,求证:AB与CD不能互相平分.
16.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
17.一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离,弧的中点到弧所对弦的距离,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?(结果精确到)
18.如图,是的直径,弦于点,点在上,恰好经过圆心,连接.
(1)若,,求的直径;
(2)若,求的度数.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,
如图所示.直径ED⊥AB于点M,
则ED=10cm,AB=8cm,
由垂径定理知:点M为AB中点,
∴AM=4cm,
∵半径OA=5cm,
∴OM2=OA2-AM2=25-16=9,
∴OM=3cm.
故选:C.
2.A
【解析】解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:A.
3.D
【解析】解:O为圆心的两个同心圆的圆心,大圆的弦AB与小圆相切于C点,
C点是AB的中点,即AC=BC==6;
并且OC⊥AB,在中,
由勾股定理得,
所以;AO=8cm,
所以,
所以OC=
故选:
4.B
【解析】解:作圆的直径CE⊥AB于点D,连接OA,
∵AB=8,
∴AD=4.
∵OA=5,
∴OD==3,
∴CD=OC-3=5-3=2,即C到弦AB所在的直线距离为2,
∴在劣弧AB上,到弦AB所在的直线距离为2的点只有C点;
∵DE=5+3=8>2,
∴在优弧AEB上到弦AB所在的直线距离为2的点有2个,即圆上到弦AB所在的直线距离为2的点有3个.
故选:B.
5.A
【解析】解:过A点作AH⊥BD于H,连接OM,如图,
在Rt△ABD中,BD=,
∵×AH×BD=×AD×AB,
∴AH==36,
∵⊙O的半径为26,
∴点O在AH上时,OH最短,
∵HM=,
∴此时HM有最大值,最大值为:
24,
∵OH⊥MN,
∴MN=2MH,
∴MN的最大值为2×24=48.
故选:A.
6.C
【解析】解:作⊙O的半径OC⊥AB于D,连接OA、AC,如图,
∵圆折叠后,圆弧恰好经过圆心,
∴AB垂直平分OC,
∴AC=AO,
而OA=OC,
∴OA=AC=OC,
∴△AOC为等边三角形,
∴∠AOC=60°,
∴OD=OA=2,
∴AD=OD=2,
∵OD⊥AB,
∴AD=BD,
∴AB=2AD=4(cm).
故选:C.
7.120°
【解析】如图,作OD⊥AB,由垂径定理知,点D是AB的中点,
∴AD=AB=(cm),
∵ cos A=,
∴∠A=,
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
故答案为:120°.
8.14cm或2cm
【解析】解:如图①,连接OA,OC,过点O作OE⊥AB,交CD于点F,交AB于点E,
因为AB//CD ,所以OE⊥CD,
∴Rt△OAE中,OA=10cm,AE=AB=6cm;
OE==8cm;
同理可得:OF=6cm;
故EF=OE-OF=2cm;
如图②;同(1)可得:OE=8cm,OF=6cm;
故EF=OE+OF=14cm;
所以AB与CD的距离是14cm或2cm,
故答案为:14cm或2cm.
9.
【解析】解:由题意得:,,
,
,
,
是等腰直角三角形,
,
故答案为:.
10.
【解析】解:连接OA
∵C是AB的中点,OA=OB,AB=4
∴AC=AB=2,OC⊥AB,
∴OA2=OC2+AC2,
∵CD=1
∴OA2=(OA-1)2+22,
解得,OA=
故答案为:
11.10
【解析】解:∵弦米,半径弦,
∴,
∴,
∴,
∴弧田面积(弦×矢+矢2),
故答案为10
12.4
【解析】解:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,
则P点有4个.
故答案为:4
13.7cm或17cm.
【解析】解:①当弦AB和CD在圆心同侧时,如图1
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12 5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
14.答案见解析.
【解析】如图,作直线OM,以M为圆心,以MO为半径作弧,交直线MO于点N,
分别以点O,点N为圆心,以大于ON为半径画弧,
二弧交于点E,F,作直线EF交圆O于A,B两点,
则弦AB即为所求.
15.见解析
【解析】解:设AB,CD交于点P,连接OP,
假设AB与CD能互相平分,则CP=DP,AP=BP,
∵AB,CD是圆O内非直径的两弦,
∴OP⊥AB,OP⊥CD,
这与“过一点有且只有一条直线与已知直线垂直相矛盾”,所以假设不成立,
所以AB与CD不能互相平分
16.证明见解析.
【解析】过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
17.半径约为.
【解析】解:如图,连接 由垂径定理推论可得:∠OCA=90°,
设圆的半径为r,则CO=r-0.25,AC=0.36,
OC2+AC2=AO2, 即0.362+(r-0.25)2=r2.
解得:r=0.3842≈0.384.
答:这个车轮的半径为0.384m.
18.(1)20;(2)30°
【解析】解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设,
又∵BE=4,
∴
∴,
解得:,
∴⊙O的直径是20.
(2)∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M=2∠B,
∵∠DOB+∠D=90°,
∴2∠B+∠D=90°,
∵,
∴∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°;
答案第1页,共2页
答案第1页,共2页
3.3垂径定理-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,则OM的长为( )
A.9cm B.6cm C.3cm D.cm
2.AB和CD是⊙O的两条平行弦,AB=6,CD=8,⊙O的半径为5,则AB与CD间的距离为( )
A.1或7 B.7 C.1 D.3或4
3.如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于C点,AB=12cm,AO=8cm,则OC长为( )cm
A.5 B.4 C. D.
4.如图,已知的半径为5,弦,则上到弦所在直线的距离为2的点有( )
A.4个 B.3个 C.2个 D.1个
5.如图,矩形中,,,,分别是,边上的动点,,以为直径的与交于点,.则的最大值为( ).
A.48 B.45 C.42 D.40
6.如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.2 B.4 C.4 D.2
二、填空题
7.半径为2cm的⊙O中,弦长为2cm的弦所对的圆心角度数为 ____.
8.已知的半径为,弦,且,则弦和之间的距离为_______.
9.如图,在⊙O中,弦的长为4,圆心到弦的距离为2,则的度数为______.
10.如图,是的弦,是的中点,连接并延长交于点.若,则的半径是_________.
11.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径⊥弦时,平分)可以求解.现已知弦米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.
12.如图,⊙O的半径为6,的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有_____个.
三、解答题
13.的半径为13cm,AB、CD是的两条弦,,AB=24cm,CD=10cm,求AB和CD之间的距离.
14.如图,M为内一点,利用尺规作一条弦,使过点M,并且.
15.如图,已知AB,CD是⊙O内非直径的两弦,求证:AB与CD不能互相平分.
16.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
17.一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离,弧的中点到弧所对弦的距离,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?(结果精确到)
18.如图,是的直径,弦于点,点在上,恰好经过圆心,连接.
(1)若,,求的直径;
(2)若,求的度数.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,
如图所示.直径ED⊥AB于点M,
则ED=10cm,AB=8cm,
由垂径定理知:点M为AB中点,
∴AM=4cm,
∵半径OA=5cm,
∴OM2=OA2-AM2=25-16=9,
∴OM=3cm.
故选:C.
2.A
【解析】解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图所示:
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3,E、F、O在一条直线上,
∴EF为AB、CD之间的距离
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE3,
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2
∴OF4,
∴EF=OE+OF=3+4=7,
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
同①可得:OE=3,OF=4;
则AB与CD的距离为:OF﹣OE=1;
综上所述:AB与CD间的距离为1或7.
故选:A.
3.D
【解析】解:O为圆心的两个同心圆的圆心,大圆的弦AB与小圆相切于C点,
C点是AB的中点,即AC=BC==6;
并且OC⊥AB,在中,
由勾股定理得,
所以;AO=8cm,
所以,
所以OC=
故选:
4.B
【解析】解:作圆的直径CE⊥AB于点D,连接OA,
∵AB=8,
∴AD=4.
∵OA=5,
∴OD==3,
∴CD=OC-3=5-3=2,即C到弦AB所在的直线距离为2,
∴在劣弧AB上,到弦AB所在的直线距离为2的点只有C点;
∵DE=5+3=8>2,
∴在优弧AEB上到弦AB所在的直线距离为2的点有2个,即圆上到弦AB所在的直线距离为2的点有3个.
故选:B.
5.A
【解析】解:过A点作AH⊥BD于H,连接OM,如图,
在Rt△ABD中,BD=,
∵×AH×BD=×AD×AB,
∴AH==36,
∵⊙O的半径为26,
∴点O在AH上时,OH最短,
∵HM=,
∴此时HM有最大值,最大值为:
24,
∵OH⊥MN,
∴MN=2MH,
∴MN的最大值为2×24=48.
故选:A.
6.C
【解析】解:作⊙O的半径OC⊥AB于D,连接OA、AC,如图,
∵圆折叠后,圆弧恰好经过圆心,
∴AB垂直平分OC,
∴AC=AO,
而OA=OC,
∴OA=AC=OC,
∴△AOC为等边三角形,
∴∠AOC=60°,
∴OD=OA=2,
∴AD=OD=2,
∵OD⊥AB,
∴AD=BD,
∴AB=2AD=4(cm).
故选:C.
7.120°
【解析】如图,作OD⊥AB,由垂径定理知,点D是AB的中点,
∴AD=AB=(cm),
∵ cos A=,
∴∠A=,
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
故答案为:120°.
8.14cm或2cm
【解析】解:如图①,连接OA,OC,过点O作OE⊥AB,交CD于点F,交AB于点E,
因为AB//CD ,所以OE⊥CD,
∴Rt△OAE中,OA=10cm,AE=AB=6cm;
OE==8cm;
同理可得:OF=6cm;
故EF=OE-OF=2cm;
如图②;同(1)可得:OE=8cm,OF=6cm;
故EF=OE+OF=14cm;
所以AB与CD的距离是14cm或2cm,
故答案为:14cm或2cm.
9.
【解析】解:由题意得:,,
,
,
,
是等腰直角三角形,
,
故答案为:.
10.
【解析】解:连接OA
∵C是AB的中点,OA=OB,AB=4
∴AC=AB=2,OC⊥AB,
∴OA2=OC2+AC2,
∵CD=1
∴OA2=(OA-1)2+22,
解得,OA=
故答案为:
11.10
【解析】解:∵弦米,半径弦,
∴,
∴,
∴,
∴弧田面积(弦×矢+矢2),
故答案为10
12.4
【解析】解:过O作OC⊥AB于C,则AC=BC,
设OC=x,AC=y,
∵AB是⊙O的一条弦,⊙O的半径为6,
∴AB≤12,
∵△OAB的面积为18,
∴,
则y=,
∴,
解得x=3或﹣3(舍),
∴OC=3>4,
∴4<OP≤6,
∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,
则P点有4个.
故答案为:4
13.7cm或17cm.
【解析】解:①当弦AB和CD在圆心同侧时,如图1
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12 5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
14.答案见解析.
【解析】如图,作直线OM,以M为圆心,以MO为半径作弧,交直线MO于点N,
分别以点O,点N为圆心,以大于ON为半径画弧,
二弧交于点E,F,作直线EF交圆O于A,B两点,
则弦AB即为所求.
15.见解析
【解析】解:设AB,CD交于点P,连接OP,
假设AB与CD能互相平分,则CP=DP,AP=BP,
∵AB,CD是圆O内非直径的两弦,
∴OP⊥AB,OP⊥CD,
这与“过一点有且只有一条直线与已知直线垂直相矛盾”,所以假设不成立,
所以AB与CD不能互相平分
16.证明见解析.
【解析】过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
17.半径约为.
【解析】解:如图,连接 由垂径定理推论可得:∠OCA=90°,
设圆的半径为r,则CO=r-0.25,AC=0.36,
OC2+AC2=AO2, 即0.362+(r-0.25)2=r2.
解得:r=0.3842≈0.384.
答:这个车轮的半径为0.384m.
18.(1)20;(2)30°
【解析】解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设,
又∵BE=4,
∴
∴,
解得:,
∴⊙O的直径是20.
(2)∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M=2∠B,
∵∠DOB+∠D=90°,
∴2∠B+∠D=90°,
∵,
∴∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°;
答案第1页,共2页
答案第1页,共2页
