2021-2022学年北师大版九年级数学下册1.6 利用三角函数测高 课堂练习(word版 含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.6 利用三角函数测高 课堂练习(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 430.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 07:35:31 | ||
图片预览



文档简介
2021-2022年初中数学九年级下册同步(北师大版)
1.6利用三角函数测高-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
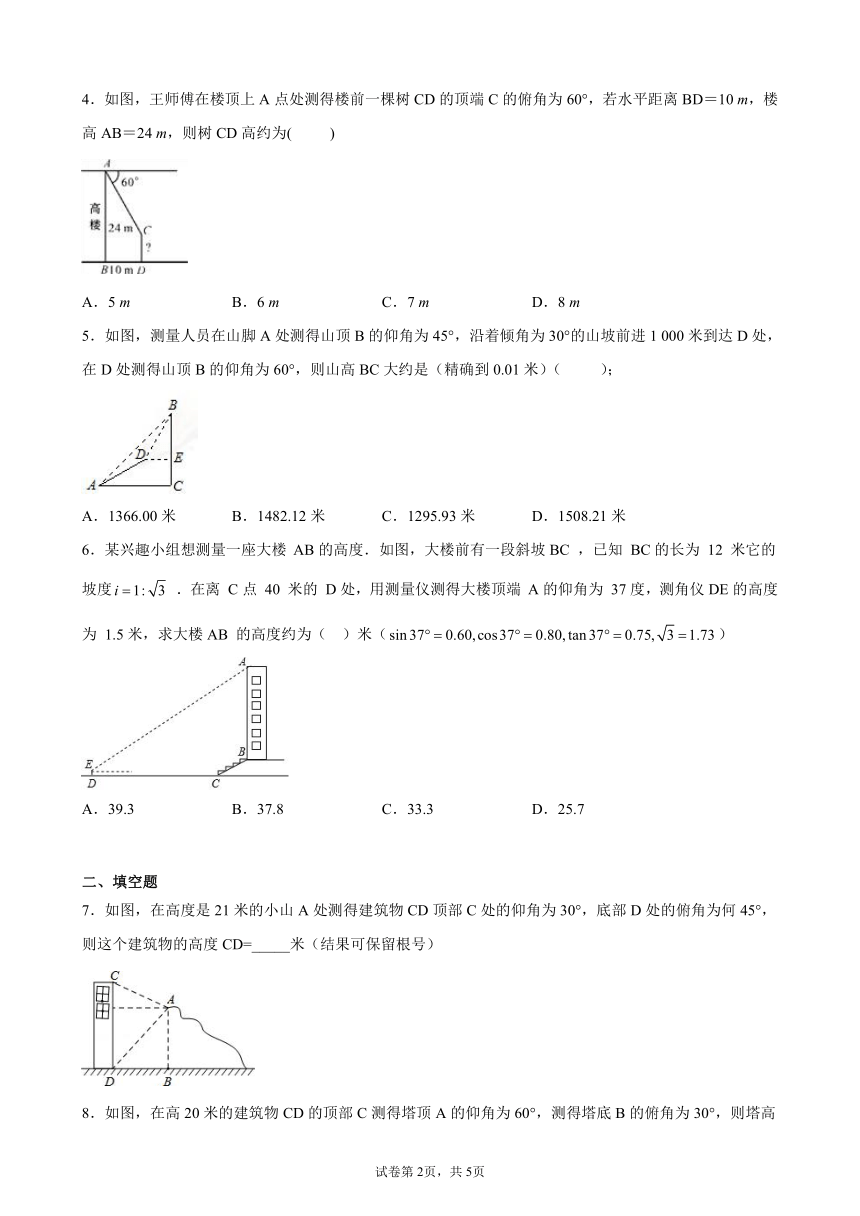
1.使用测倾器测量倾斜角的步骤有:(1)记下此时铅垂线所指的度数;(2)使支杆的中心线、铅垂线和度盘的刻度线重合;(3)转动度盘,使度盘的直径对准目标M;(4)把支杆竖直插入地面.则正确的步骤应为( )
A.(1)(2)(3)(4) B.(4)(3)(2)(1)
C.(4)(2)(3)(1) D.(3)(4)(2)(1)
2.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B. C. D.
3.为扩大网络信号的辐射范围,某通信公司在一座小山上新建了一座大型的网络信号发射塔.如图,在高为12米的建筑物DE的顶部测得信号发射塔AB顶端的仰角∠FEA=56°,建筑物DE的底部D到山脚底部C的距离DC=16米,小山坡面BC的坡度(或坡比)i=1:0.75,坡长BC=40米(建筑物DE、小山坡BC和网络信号发射塔AB的剖面图在同一平面内,信号发射塔AB与水平线DC垂直),则信号发射塔AB的高约为 ( )(参考数据:sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
A.71.4米 B.59.2米 C.48.2米 D.39.2米
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )
A.5 m B.6 m C.7 m D.8 m
5.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.01米)( );
A.1366.00米 B.1482.12米 C.1295.93米 D.1508.21米
6.某兴趣小组想测量一座大楼 AB的高度.如图,大楼前有一段斜坡BC ,已知 BC的长为 12 米它的坡度 .在离 C点 40 米的 D处,用测量仪测得大楼顶端 A的仰角为 37度,测角仪DE的高度为 1.5米,求大楼AB 的高度约为( )米()
A.39.3 B.37.8 C.33.3 D.25.7
二、填空题
7.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为何45°,则这个建筑物的高度CD=_____米(结果可保留根号)
8.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = ______米;
9.如图,某同学用一个有角的直角三角板估测学校旗杆AB的高度.他将与角相邻的直角边水平放在1.5m高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB的距离为5m,则旗杆AB的高度约为________m.(结果精确到lm,取1.73)
10.小明在热气球上看到正前方横跨河流两岸的大桥,并测得、两点的俯角分别为45°、35°.已知大桥与地面在同一水平面上,其长度为,求热气球离地面的高度_________.(结果保留整数)(参考数据:,,)
11.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC=___米(结果保留根号).
12.某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测得操控者A和教学楼BC距离为57米,则教学楼BC的高度为______米.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
三、解答题
13.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,求旗杆AB的高度(精确到0.01米).
14.如图,在高出海平面的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为,求船与观测者之间的水平距离(结果精确到).
15.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:≈1.414,≈1.732)
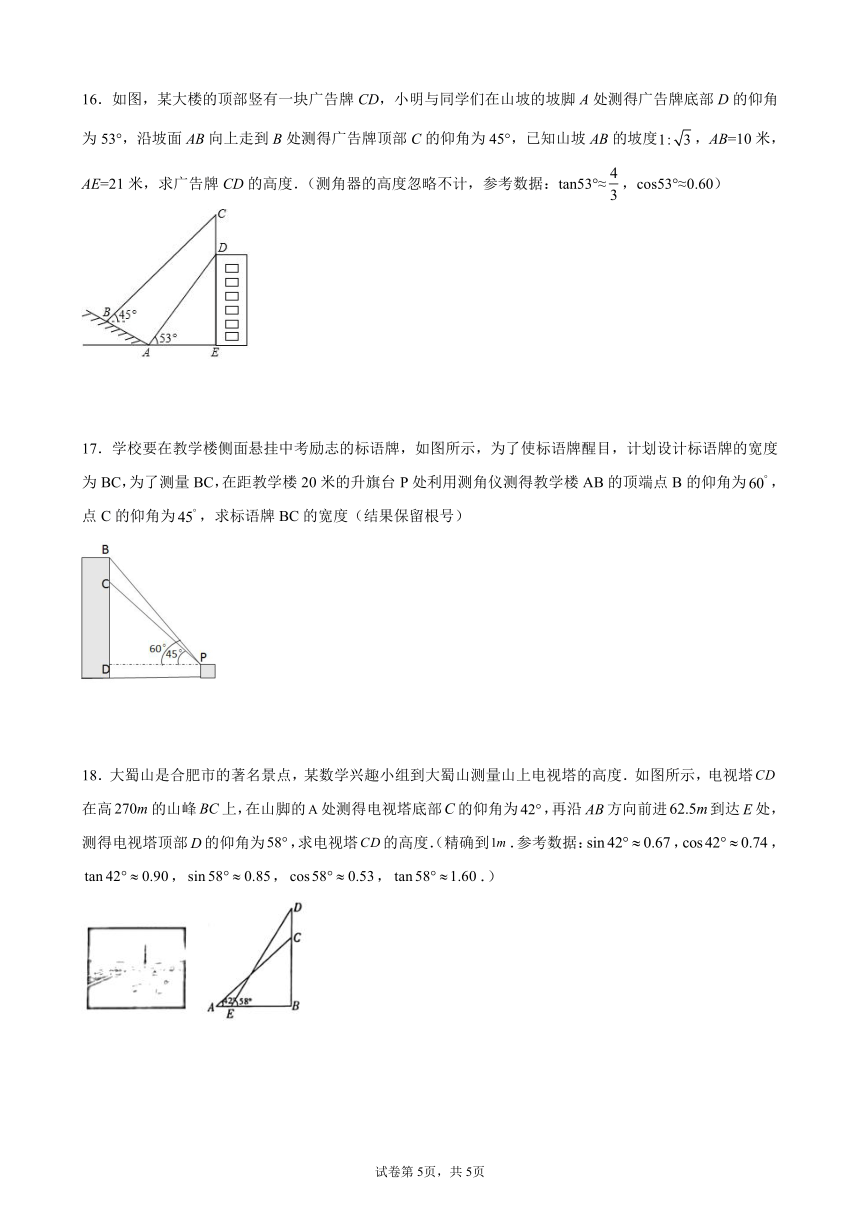
16.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈,cos53°≈0.60)
17.学校要在教学楼侧面悬挂中考励志的标语牌,如图所示,为了使标语牌醒目,计划设计标语牌的宽度为BC,为了测量BC,在距教学楼20米的升旗台P处利用测角仪测得教学楼AB的顶端点B的仰角为,点C的仰角为,求标语牌BC的宽度(结果保留根号)
18.大蜀山是合肥市的著名景点,某数学兴趣小组到大蜀山测量山上电视塔的高度.如图所示,电视塔在高的山峰上,在山脚的处测得电视塔底部的仰角为,再沿方向前进到达处,测得电视塔顶部的仰角为,求电视塔的高度.(精确到.参考数据:,,,,,.)
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:使用测倾器测量倾斜角的步骤有:把支杆竖直插入地面;使支杆的中心线、铅垂线和度盘的 刻度线重合;转动度盘,使度盘的直径对准目标M;记下此时铅垂线所指的度数;所以正确的顺序是:(4)(2)(3)(1);
故选择:C.
2.A
【解析】如图,延长BA、FE,交于点D.
∵AB⊥BC,EF∥BC,
∴BD⊥DF,即∠ADE=90°.
∵∠AEF=143°,
∴∠AED=37°.
在Rt△ADE中,
∵sin∠AED,AE=1.2米,
∴AD=AE sin∠AED=1.2×sin37°≈0.72(米),
则BD=AB+AD=1.18+0.72=1.9(米).
故选:A.
3.D
【解析】解:如图,延长EF交AB于点H,DC⊥AB于点G,
∵ED⊥DG,
∴四边形EDGH是矩形,
∴GH=ED=12,
∵小山坡面BC的坡度i=1:0.75,即,
设BG=4x,CG=3x,则BC=5x,
∵BC=40,
∴5x=40,
解得x=8,
∴BG=32,CG=24,
∴EH=DG=DC+CG=16+24=40,
BH=BG﹣GH=32﹣12=20,
在Rt△AEH中,∠AEH=56°,
∴AH=EH tan56°≈40×1.48≈59.2,
∴AB=AH﹣BH=59.2﹣20=39.2(米).
答:信号发射塔AB的高约为39.2米.
故选:D.
4.C
【解析】过点C作AB的垂线CE,在Rt△AEC中,CE=BD=10, ∠CAE=30°,因为所以,AE=,
所以CD=BE=AB-AE=24-10故选C.
5.A
【解析】解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DF⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=AD=500,
∴EC=500,BE=1000×sin60°=500.
∴BC=500+500(米).
故选A
6.C
【解析】解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,=,
∴设BF=k,则CF=k,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=,
∵DF=DC+CF,
∴DF=40+,
∵在Rt△AEH中,tan∠AEH=,
∴AH=tan37°×(40+)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
故选C.
7.21+7或7+21
【解析】解:作AE⊥CD于点E.
在Rt△ABD中,∠ADB=45°,
∴DE=AE=BD=AB=21(米).
在Rt△AEC中,CE=AE tan∠CAE=21×=7.
∴CD=21+7(米).
故答案为:21+7.
8.80
【解析】
解:作CE⊥AB,垂足为E.
在Rt△BCE中,BE=CD=20,CE=BE÷tan30°=20,
在Rt△ACE中,可得AE=CE×tan60°=20=60,
故AB=AE+EB=60+20=80(米).
故答案为:80
9.10
【解析】解:由题意可知,在△ACE中,CE⊥AE,且∠ACE=60°,BD=5,
而tan∠ACE=,
∴AE=CE×tan60°=≈8.6.
又∵EB=1.5,
∴AB=AE+EB≈10(米).
故答案为10.
10.233m
【解析】解:作AD⊥BC交CB的延长线于D,设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
,
,
解得,x≈233.
所以,热气球离地面的高度约为233米.
故答案为:233.
11..
【解析】解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:.
12.13
【解析】解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
由题意得,AB=57,DE=30,∠A=37°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan37°=≈0.75.
∴AE=40,
∵AB=57,
∴BE=17
∵四边形BCFE是矩形,
∴CF=BE=17.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=17,
∴BC=EF=30-17=13.
故答案为:13.
13.15.54米
【解析】解:在Rt△ACE中,∠ACE=α=35°,CE=BD=20,
∴tan∠ACE=,
∴AE=CE tan∠ACE=20 tan35°,
∴AB=AE+BE= 14.004+1.54≈15.54(米).
14.
【解析】解:∵在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为30°,
∴tan30°=,
∴船与观测者之间的水平距离BC=AC÷tan30°=100÷≈173.2米.
答:船与观测者之间的水平距离为173.2m.
15.这棵树CD的高度为8.7米
【解析】∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10×=5≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
16.
【解析】解:过B作BG⊥DE于G,BH⊥AE,
Rt△ABH中,i=tan∠BAH==,
∴∠BAH=30°,
∴BH=AB=5米;
∴AH=5米,
∴BG=HE=AH+AE=(5+21)米,
Rt△BGC中,∠CBG=45°,
∴CG=BG=(5+21)米.
Rt△ADE中,∠DAE=53°,AE=21米,
∴DE=AE=28米,
∴CD=CG+GE﹣DE=26+5﹣28=(5﹣2)m.
答:宣传牌CD高为()米.
17.BC=
【解析】解:由题意知,PD=20,,
在中,,
则,
在中,,
,
,
故答案为:.
18.电视塔CD的高度约为110 m.
【解析】在Rt△ABC中,,
∴m,
∵AE=62.5m,
∴m,
在Rt△BED中,,
∴m,
∴m.
答:电视塔CD的高度约为110 m.
答案第1页,共2页
答案第1页,共2页
1.6利用三角函数测高-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.使用测倾器测量倾斜角的步骤有:(1)记下此时铅垂线所指的度数;(2)使支杆的中心线、铅垂线和度盘的刻度线重合;(3)转动度盘,使度盘的直径对准目标M;(4)把支杆竖直插入地面.则正确的步骤应为( )
A.(1)(2)(3)(4) B.(4)(3)(2)(1)
C.(4)(2)(3)(1) D.(3)(4)(2)(1)
2.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B. C. D.
3.为扩大网络信号的辐射范围,某通信公司在一座小山上新建了一座大型的网络信号发射塔.如图,在高为12米的建筑物DE的顶部测得信号发射塔AB顶端的仰角∠FEA=56°,建筑物DE的底部D到山脚底部C的距离DC=16米,小山坡面BC的坡度(或坡比)i=1:0.75,坡长BC=40米(建筑物DE、小山坡BC和网络信号发射塔AB的剖面图在同一平面内,信号发射塔AB与水平线DC垂直),则信号发射塔AB的高约为 ( )(参考数据:sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
A.71.4米 B.59.2米 C.48.2米 D.39.2米
4.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )
A.5 m B.6 m C.7 m D.8 m
5.如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.01米)( );
A.1366.00米 B.1482.12米 C.1295.93米 D.1508.21米
6.某兴趣小组想测量一座大楼 AB的高度.如图,大楼前有一段斜坡BC ,已知 BC的长为 12 米它的坡度 .在离 C点 40 米的 D处,用测量仪测得大楼顶端 A的仰角为 37度,测角仪DE的高度为 1.5米,求大楼AB 的高度约为( )米()
A.39.3 B.37.8 C.33.3 D.25.7
二、填空题
7.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为何45°,则这个建筑物的高度CD=_____米(结果可保留根号)
8.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = ______米;
9.如图,某同学用一个有角的直角三角板估测学校旗杆AB的高度.他将与角相邻的直角边水平放在1.5m高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB的距离为5m,则旗杆AB的高度约为________m.(结果精确到lm,取1.73)
10.小明在热气球上看到正前方横跨河流两岸的大桥,并测得、两点的俯角分别为45°、35°.已知大桥与地面在同一水平面上,其长度为,求热气球离地面的高度_________.(结果保留整数)(参考数据:,,)
11.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC=___米(结果保留根号).
12.某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测得操控者A和教学楼BC距离为57米,则教学楼BC的高度为______米.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
三、解答题
13.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,求旗杆AB的高度(精确到0.01米).
14.如图,在高出海平面的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为,求船与观测者之间的水平距离(结果精确到).
15.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:≈1.414,≈1.732)
16.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,参考数据:tan53°≈,cos53°≈0.60)
17.学校要在教学楼侧面悬挂中考励志的标语牌,如图所示,为了使标语牌醒目,计划设计标语牌的宽度为BC,为了测量BC,在距教学楼20米的升旗台P处利用测角仪测得教学楼AB的顶端点B的仰角为,点C的仰角为,求标语牌BC的宽度(结果保留根号)
18.大蜀山是合肥市的著名景点,某数学兴趣小组到大蜀山测量山上电视塔的高度.如图所示,电视塔在高的山峰上,在山脚的处测得电视塔底部的仰角为,再沿方向前进到达处,测得电视塔顶部的仰角为,求电视塔的高度.(精确到.参考数据:,,,,,.)
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:使用测倾器测量倾斜角的步骤有:把支杆竖直插入地面;使支杆的中心线、铅垂线和度盘的 刻度线重合;转动度盘,使度盘的直径对准目标M;记下此时铅垂线所指的度数;所以正确的顺序是:(4)(2)(3)(1);
故选择:C.
2.A
【解析】如图,延长BA、FE,交于点D.
∵AB⊥BC,EF∥BC,
∴BD⊥DF,即∠ADE=90°.
∵∠AEF=143°,
∴∠AED=37°.
在Rt△ADE中,
∵sin∠AED,AE=1.2米,
∴AD=AE sin∠AED=1.2×sin37°≈0.72(米),
则BD=AB+AD=1.18+0.72=1.9(米).
故选:A.
3.D
【解析】解:如图,延长EF交AB于点H,DC⊥AB于点G,
∵ED⊥DG,
∴四边形EDGH是矩形,
∴GH=ED=12,
∵小山坡面BC的坡度i=1:0.75,即,
设BG=4x,CG=3x,则BC=5x,
∵BC=40,
∴5x=40,
解得x=8,
∴BG=32,CG=24,
∴EH=DG=DC+CG=16+24=40,
BH=BG﹣GH=32﹣12=20,
在Rt△AEH中,∠AEH=56°,
∴AH=EH tan56°≈40×1.48≈59.2,
∴AB=AH﹣BH=59.2﹣20=39.2(米).
答:信号发射塔AB的高约为39.2米.
故选:D.
4.C
【解析】过点C作AB的垂线CE,在Rt△AEC中,CE=BD=10, ∠CAE=30°,因为所以,AE=,
所以CD=BE=AB-AE=24-10故选C.
5.A
【解析】解:∵∠BAC=45°,∠DAC=30°,
∴∠BAD=15°,
∵∠BDE=60°,∠BED=90°,
∴∠DBE=30°,
∵∠ABC=45°,
∴∠ABD=15°,
∴∠ABD=∠DAB,
∴AD=BD=1000,
过点D作DF⊥AC,
∵AC⊥BC,DF⊥AC,DE⊥BC,
∴∠DFC=∠ACB=∠DEC=90°
∴四边形DFCE是矩形
∴DF=CE
在直角三角ADF中,∵∠DAF=30°,
∴DF=AD=500,
∴EC=500,BE=1000×sin60°=500.
∴BC=500+500(米).
故选A
6.C
【解析】解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,=,
∴设BF=k,则CF=k,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=,
∵DF=DC+CF,
∴DF=40+,
∵在Rt△AEH中,tan∠AEH=,
∴AH=tan37°×(40+)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
故选C.
7.21+7或7+21
【解析】解:作AE⊥CD于点E.
在Rt△ABD中,∠ADB=45°,
∴DE=AE=BD=AB=21(米).
在Rt△AEC中,CE=AE tan∠CAE=21×=7.
∴CD=21+7(米).
故答案为:21+7.
8.80
【解析】
解:作CE⊥AB,垂足为E.
在Rt△BCE中,BE=CD=20,CE=BE÷tan30°=20,
在Rt△ACE中,可得AE=CE×tan60°=20=60,
故AB=AE+EB=60+20=80(米).
故答案为:80
9.10
【解析】解:由题意可知,在△ACE中,CE⊥AE,且∠ACE=60°,BD=5,
而tan∠ACE=,
∴AE=CE×tan60°=≈8.6.
又∵EB=1.5,
∴AB=AE+EB≈10(米).
故答案为10.
10.233m
【解析】解:作AD⊥BC交CB的延长线于D,设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
,
,
解得,x≈233.
所以,热气球离地面的高度约为233米.
故答案为:233.
11..
【解析】解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:.
12.13
【解析】解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
由题意得,AB=57,DE=30,∠A=37°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan37°=≈0.75.
∴AE=40,
∵AB=57,
∴BE=17
∵四边形BCFE是矩形,
∴CF=BE=17.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=17,
∴BC=EF=30-17=13.
故答案为:13.
13.15.54米
【解析】解:在Rt△ACE中,∠ACE=α=35°,CE=BD=20,
∴tan∠ACE=,
∴AE=CE tan∠ACE=20 tan35°,
∴AB=AE+BE= 14.004+1.54≈15.54(米).
14.
【解析】解:∵在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为30°,
∴tan30°=,
∴船与观测者之间的水平距离BC=AC÷tan30°=100÷≈173.2米.
答:船与观测者之间的水平距离为173.2m.
15.这棵树CD的高度为8.7米
【解析】∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10×=5≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
16.
【解析】解:过B作BG⊥DE于G,BH⊥AE,
Rt△ABH中,i=tan∠BAH==,
∴∠BAH=30°,
∴BH=AB=5米;
∴AH=5米,
∴BG=HE=AH+AE=(5+21)米,
Rt△BGC中,∠CBG=45°,
∴CG=BG=(5+21)米.
Rt△ADE中,∠DAE=53°,AE=21米,
∴DE=AE=28米,
∴CD=CG+GE﹣DE=26+5﹣28=(5﹣2)m.
答:宣传牌CD高为()米.
17.BC=
【解析】解:由题意知,PD=20,,
在中,,
则,
在中,,
,
,
故答案为:.
18.电视塔CD的高度约为110 m.
【解析】在Rt△ABC中,,
∴m,
∵AE=62.5m,
∴m,
在Rt△BED中,,
∴m,
∴m.
答:电视塔CD的高度约为110 m.
答案第1页,共2页
答案第1页,共2页
