2021-2022学年青岛版九年级下册数学第5章对函数的再探索单元测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版九年级下册数学第5章对函数的再探索单元测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 98.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 09:55:51 | ||
图片预览




文档简介
2021-2022学年青岛新版九年级下册数学《第5章 对函数的再探索》单元测试卷
一.选择题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,这个问题中因变量是( )
A.水的温度 B.太阳光强弱
C.太阳照射时间 D.热水器的容积
2.球的体积V与半径R之间的关系式为V=πR3,下列说法正确的是( )
A.变量为V,R,常量为π,3
B.变量为V,R,常量为,π
C.变量为V,R,π,常量为
D.变量为V,R3,常量为π
3.明明从广州给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个过程中,因变量是( )
A.明明 B.电话费 C.时间 D.爷爷
4.下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) 1 2 3 4 …
应交电费y(元) 0.55 1.1 1.65 2.2 …
A.x与y都是变量,且x是自变量,y是x的函数
B.用电量每增加1千瓦时,电费增加0.55元
C.若用电量为8千瓦时,则应交电费4.4元
D.y不是x的函数
5.若函数y=(2m﹣1)x是反比例函数,则m的值是( )
A.﹣1或1 B.小于的任意实数
C.﹣1 D.1
6.已知函数y=(m+1)是反比例函数,则m的值为( )
A.1 B.﹣1 C.1或﹣1 D.任意实数
7.已知正比例函数y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象有一个交点的坐标为(﹣2,﹣1),则它的另一个交点的坐标是( )
A.(2,1) B.(﹣2,﹣1) C.(﹣2,1) D.(2,﹣1)
8.小颖现已存款200元.为赞助“希望工程”,她计划今后每月存款10元,则存款总金额y(元)与时间x(月)之间的函数关系式是( )
A.y=10x B.y=120x C.y=200﹣10x D.y=200+10x
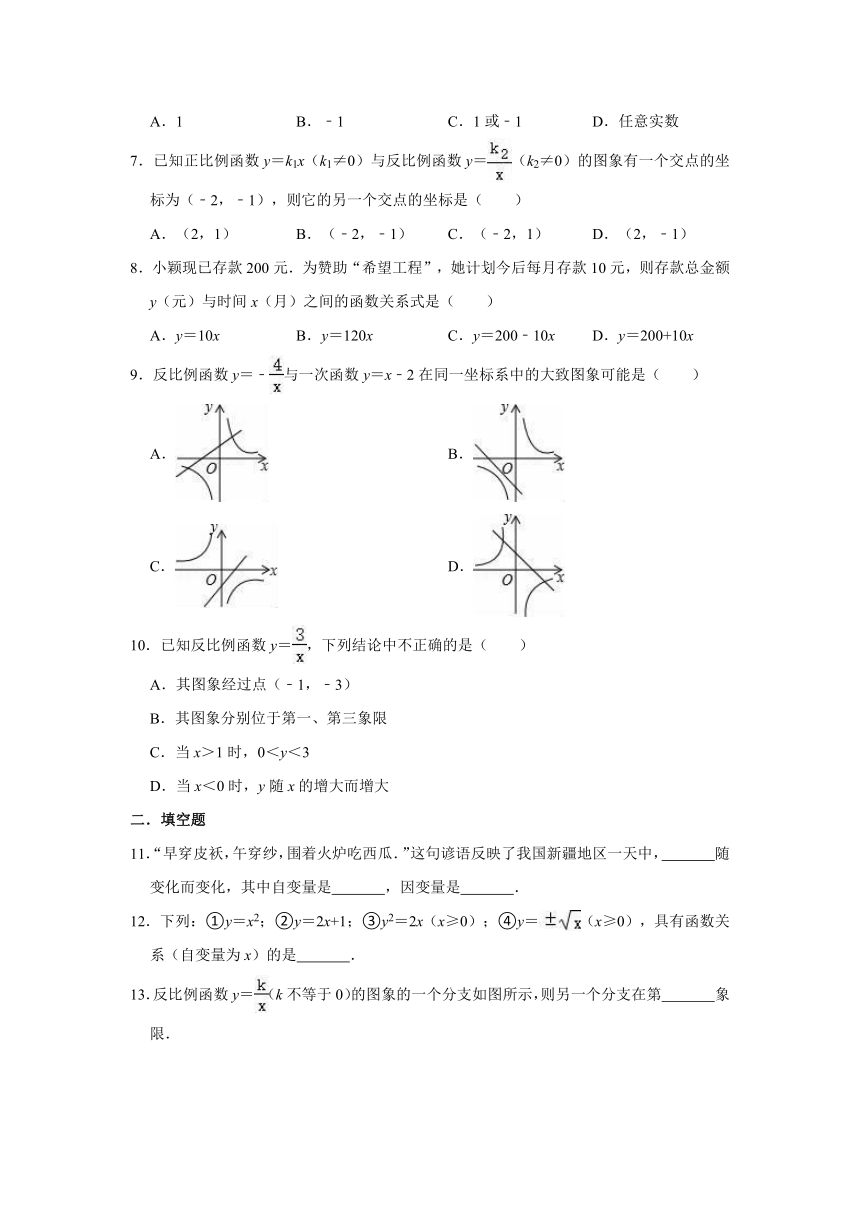
9.反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )
A. B.
C. D.
10.已知反比例函数y=,下列结论中不正确的是( )
A.其图象经过点(﹣1,﹣3)
B.其图象分别位于第一、第三象限
C.当x>1时,0<y<3
D.当x<0时,y随x的增大而增大
二.填空题
11.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 随 变化而变化,其中自变量是 ,因变量是 .
12.下列:①y=x2;②y=2x+1;③y2=2x(x≥0);④y=(x≥0),具有函数关系(自变量为x)的是 .
13.反比例函数y=(k不等于0)的图象的一个分支如图所示,则另一个分支在第 象限.
14.直线y=2x与双曲线y=的图象的一个交点为(2,4),则它们的另一个交点的坐标是 .
15.如果三角形底边上的高是6,底边长为x,那么三角形的面积y与底边长x的关系为 .
16.3x﹣y=7中,变量是 ,常量是 .把它写成用x的式子表示y的形式是 .
17.函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值为 .
18.已知函数,当x=﹣2时,y的值是 .
19.若反比例函数y=的图象有一支在第二象限,则k的取值范围是 .
20.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 .
三.解答题
21.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁的2倍、3倍.
(1)上述的哪些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
22.已知反比例函数y=(3m﹣1)的图象在第二、四象限,求m的值.
23.如图是一位病人的体温记录图,看图回答下列问题:
(1)自变量是 ,因变量是 ;
(2)护士每隔 小时给病人量一次体温;
(3)这位病人的最高体温是 摄氏度,最低体温是 摄氏度;
(4)他在4月8日12时的体温是 摄氏度;
(5)图中的横虚线表示 ;
24.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
25.阅读下面材料,再回答问题.
一般地,如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=f(x).那么y=f(x)就叫偶函数.如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=﹣f(x).那么y=f(x)就叫奇函数.
例如:f(x)=x4
当x取任意实数时,f(﹣x)=(﹣x)4=x4∴f(﹣x)=f(x)∴f(x)=x4是偶函数.
又如:f(x)=2x3﹣x.
当x取任意实数时,∵f(﹣x)=2(﹣x)3﹣(﹣x)=﹣2x3+x=﹣(2x3﹣x)∴f(﹣x)=﹣f(x)∴f(x)=2x3﹣x是奇函数.
问题1:下列函数中:①y=x2+1②③④⑤y=x﹣2﹣2|x|
是奇函数的有 ;是偶函数的有 (填序号)
问题2:仿照例证明:函数④或⑤是奇函数还是偶函数(选择其中之一)
26.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价30元,乒乓球每盒定价5元,现两家商店搞促销活动,甲店:每买一副球拍赠一盒乒乓球;乙店:按定价的9折优惠,某班级需购球拍4副,乒乓球若干盒(不少于4盒).
(1)设购买乒乓球为x盒,在甲店购买的付款金额为y甲元,在乙店购买的付款金额为y乙元,分别写出在两家商店购买的付款金额与乒乓球盒数x之间的表达式;
(2)购买几盒乒乓球去两家商店付款金额一样?
27.y是x的反比例函数,下表给出了x与y的一些值:
x ﹣2 ﹣1 ﹣ 1 3
y 2 ﹣1
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.
参考答案与试题解析
一.选择题
1.解:根据函数的定义可知,水温是随着所晒时间的长短而变化,可知水温是因变量,所晒时间为自变量.
故选:A.
2.解:V=πR3中,变量为V,R,常量为,π,
故选:B.
3.解:∵电话费随着时间的变化而变化,
∴自变量是时间,因变量是电话费;
故选:B.
4.解:A、x与y都是变量,且x是自变量,y是x的函数,正确,不合题意;
B、用电量每增加1千瓦时,电费增加0.55元,正确,不合题意;
C、若用电量为8千瓦时,则应交电费4.4元,正确,不合题意;
D、y不是x的函数,错误,符合题意.
故选:D.
5.解:依题意得:m2﹣2=﹣1且2m﹣1≠0,
解得m=±1.
故选:A.
6.解:∵函数y=(m+1)是反比例函数,
∴m2﹣2=﹣1且m+1≠0,
解得m=1.
故选:A.
7.解:∵反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称,
∴它的另一个交点的坐标是(2,1).
故选:A.
8.解:由题意可得,
y=200+10x,
故选:D.
9.解:由反比例函数y=﹣与一次函数y=x﹣2可知,反比例函数的图象在二、四象限,一次函数的图象通过一、三、四象限,
故选:C.
10.解:A、∵(﹣1)×(﹣3)=3,
∴图象必经过点(﹣1,﹣3),故本选项不符合题意;
B、∵k=3>0,
∴函数图象的两个分支分布在第一、三象限,故本选项不符合题意;
C、∵x=1时,y=3且y随x的增大而增大,
∴x>1时,0<y<3,故本选项不符合题意;
D、函数图象的两个分支分布在第一、三象限,在每一象限内,y随x的增大而减小,故本选项符合题意.
故选:D.
二.填空题
11.解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
12.解:∵对于x的每一个取值,y都有唯一确定的值,
∴①y=x2;②y=2x+1当x取值时,y有唯一的值对应;
故具有函数关系(自变量为x)的是①②.
故答案为:①②.
13.解:根据反比例函数反比例函数图象特点:
当y=(k不等于0)的图象的一个分支在第二象限,则另一个分支在第四象限.
故填四.
14.解:因为直线y=2x与双曲线y=的交点均关于原点对称,
所以另一个交点坐标为(﹣2,﹣4).
15.解:∵三角形底边上的高是6,底边长为x,
∴三角形的面积y=×6 x=3x,即y=3x,
故答案为:y=3x.
16.解:3x﹣y=7中,变量是x和y,常量是3和﹣7.把它写成用x的式子表示y的形式是y=3x﹣7.
故答案是:x和y;3和﹣7;y=3x﹣7.
17.解:由题意得:|m|﹣2=﹣1且,m﹣1≠0;
解得m=±1,又m≠1;
∴m=﹣1.
故填m=﹣1.
18.解:当x=﹣2时,则y=﹣=3.
故答案为:3.
19.解:∵反比例函数y=的图象有一支在第二象限,
∴k+5<0,
解得k<﹣5.
故答案为:k<﹣5.
20.解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
三.解答题
21.解:(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
22.解:∵反比例函数y=(3m﹣1)的图象在第二、四象限,
∴m2﹣2=﹣1,3m﹣1<0,
∴m=﹣1.
23.解:(1)自变量是时间,因变量是体温;
(2)护士每隔6小时给病人量一次体温;
(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(4)他在4月8日12时的体温是37.5摄氏度;
(5)图中的横虚线表示人的正常体温;
故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.
24.解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
25.解:问题1:①y=(﹣x)2+1=x2+1,
∴①是偶函数;
②y==﹣,
∴②是奇函数;
③y=≠≠﹣,
∴③既不是奇函数,也不是偶函数;
④y=﹣x+=﹣(x+),
∴④是奇函数;
⑤y=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|,
∴⑤是偶函数,
故答案为:奇函数有②④;偶函数有①⑤;
问题2:证明:④∵当x≠0时,
f(﹣x)=﹣x+=﹣(x+)=﹣f(x),
∴y=x+是奇函数,
⑤∵f(﹣x)=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|=f(x)(x≠0),
∴y=x﹣2﹣2|x|是偶函数.
26.解:(1)由题意得
y甲=30×4+5×(x﹣4)=100+5x(x≥4),
y乙=30×4×0.9+5x×0.9=4.5x+108(x≥4);
(2)当y甲=y乙时,即100+5x=4.5x+108,
解得x=16,
所以当购买16盒乒乓球时,到两店价格一样.
27.解:(1)设反比例函数的表达式为y=,把x=﹣1,y=2代入得k=﹣2,y=﹣.
(2)将y=代入得:x=﹣3;
将x=﹣2代入得:y=1;
将x=﹣代入得:y=4;
将x=代入得:y=﹣4,
将x=1代入得:y=﹣2;
将y=﹣1代入得:x=2,
将x=3代入得:y=﹣.
故答案为:﹣3;1;4;﹣4;﹣2;2;.
一.选择题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温会随着太阳照射时间的长短而变化,这个问题中因变量是( )
A.水的温度 B.太阳光强弱
C.太阳照射时间 D.热水器的容积
2.球的体积V与半径R之间的关系式为V=πR3,下列说法正确的是( )
A.变量为V,R,常量为π,3
B.变量为V,R,常量为,π
C.变量为V,R,π,常量为
D.变量为V,R3,常量为π
3.明明从广州给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个过程中,因变量是( )
A.明明 B.电话费 C.时间 D.爷爷
4.下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) 1 2 3 4 …
应交电费y(元) 0.55 1.1 1.65 2.2 …
A.x与y都是变量,且x是自变量,y是x的函数
B.用电量每增加1千瓦时,电费增加0.55元
C.若用电量为8千瓦时,则应交电费4.4元
D.y不是x的函数
5.若函数y=(2m﹣1)x是反比例函数,则m的值是( )
A.﹣1或1 B.小于的任意实数
C.﹣1 D.1
6.已知函数y=(m+1)是反比例函数,则m的值为( )
A.1 B.﹣1 C.1或﹣1 D.任意实数
7.已知正比例函数y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象有一个交点的坐标为(﹣2,﹣1),则它的另一个交点的坐标是( )
A.(2,1) B.(﹣2,﹣1) C.(﹣2,1) D.(2,﹣1)
8.小颖现已存款200元.为赞助“希望工程”,她计划今后每月存款10元,则存款总金额y(元)与时间x(月)之间的函数关系式是( )
A.y=10x B.y=120x C.y=200﹣10x D.y=200+10x
9.反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )
A. B.
C. D.
10.已知反比例函数y=,下列结论中不正确的是( )
A.其图象经过点(﹣1,﹣3)
B.其图象分别位于第一、第三象限
C.当x>1时,0<y<3
D.当x<0时,y随x的增大而增大
二.填空题
11.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 随 变化而变化,其中自变量是 ,因变量是 .
12.下列:①y=x2;②y=2x+1;③y2=2x(x≥0);④y=(x≥0),具有函数关系(自变量为x)的是 .
13.反比例函数y=(k不等于0)的图象的一个分支如图所示,则另一个分支在第 象限.
14.直线y=2x与双曲线y=的图象的一个交点为(2,4),则它们的另一个交点的坐标是 .
15.如果三角形底边上的高是6,底边长为x,那么三角形的面积y与底边长x的关系为 .
16.3x﹣y=7中,变量是 ,常量是 .把它写成用x的式子表示y的形式是 .
17.函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值为 .
18.已知函数,当x=﹣2时,y的值是 .
19.若反比例函数y=的图象有一支在第二象限,则k的取值范围是 .
20.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 .
三.解答题
21.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁的2倍、3倍.
(1)上述的哪些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
22.已知反比例函数y=(3m﹣1)的图象在第二、四象限,求m的值.
23.如图是一位病人的体温记录图,看图回答下列问题:
(1)自变量是 ,因变量是 ;
(2)护士每隔 小时给病人量一次体温;
(3)这位病人的最高体温是 摄氏度,最低体温是 摄氏度;
(4)他在4月8日12时的体温是 摄氏度;
(5)图中的横虚线表示 ;
24.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
25.阅读下面材料,再回答问题.
一般地,如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=f(x).那么y=f(x)就叫偶函数.如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=﹣f(x).那么y=f(x)就叫奇函数.
例如:f(x)=x4
当x取任意实数时,f(﹣x)=(﹣x)4=x4∴f(﹣x)=f(x)∴f(x)=x4是偶函数.
又如:f(x)=2x3﹣x.
当x取任意实数时,∵f(﹣x)=2(﹣x)3﹣(﹣x)=﹣2x3+x=﹣(2x3﹣x)∴f(﹣x)=﹣f(x)∴f(x)=2x3﹣x是奇函数.
问题1:下列函数中:①y=x2+1②③④⑤y=x﹣2﹣2|x|
是奇函数的有 ;是偶函数的有 (填序号)
问题2:仿照例证明:函数④或⑤是奇函数还是偶函数(选择其中之一)
26.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价30元,乒乓球每盒定价5元,现两家商店搞促销活动,甲店:每买一副球拍赠一盒乒乓球;乙店:按定价的9折优惠,某班级需购球拍4副,乒乓球若干盒(不少于4盒).
(1)设购买乒乓球为x盒,在甲店购买的付款金额为y甲元,在乙店购买的付款金额为y乙元,分别写出在两家商店购买的付款金额与乒乓球盒数x之间的表达式;
(2)购买几盒乒乓球去两家商店付款金额一样?
27.y是x的反比例函数,下表给出了x与y的一些值:
x ﹣2 ﹣1 ﹣ 1 3
y 2 ﹣1
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表.
参考答案与试题解析
一.选择题
1.解:根据函数的定义可知,水温是随着所晒时间的长短而变化,可知水温是因变量,所晒时间为自变量.
故选:A.
2.解:V=πR3中,变量为V,R,常量为,π,
故选:B.
3.解:∵电话费随着时间的变化而变化,
∴自变量是时间,因变量是电话费;
故选:B.
4.解:A、x与y都是变量,且x是自变量,y是x的函数,正确,不合题意;
B、用电量每增加1千瓦时,电费增加0.55元,正确,不合题意;
C、若用电量为8千瓦时,则应交电费4.4元,正确,不合题意;
D、y不是x的函数,错误,符合题意.
故选:D.
5.解:依题意得:m2﹣2=﹣1且2m﹣1≠0,
解得m=±1.
故选:A.
6.解:∵函数y=(m+1)是反比例函数,
∴m2﹣2=﹣1且m+1≠0,
解得m=1.
故选:A.
7.解:∵反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称,
∴它的另一个交点的坐标是(2,1).
故选:A.
8.解:由题意可得,
y=200+10x,
故选:D.
9.解:由反比例函数y=﹣与一次函数y=x﹣2可知,反比例函数的图象在二、四象限,一次函数的图象通过一、三、四象限,
故选:C.
10.解:A、∵(﹣1)×(﹣3)=3,
∴图象必经过点(﹣1,﹣3),故本选项不符合题意;
B、∵k=3>0,
∴函数图象的两个分支分布在第一、三象限,故本选项不符合题意;
C、∵x=1时,y=3且y随x的增大而增大,
∴x>1时,0<y<3,故本选项不符合题意;
D、函数图象的两个分支分布在第一、三象限,在每一象限内,y随x的增大而减小,故本选项符合题意.
故选:D.
二.填空题
11.解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
12.解:∵对于x的每一个取值,y都有唯一确定的值,
∴①y=x2;②y=2x+1当x取值时,y有唯一的值对应;
故具有函数关系(自变量为x)的是①②.
故答案为:①②.
13.解:根据反比例函数反比例函数图象特点:
当y=(k不等于0)的图象的一个分支在第二象限,则另一个分支在第四象限.
故填四.
14.解:因为直线y=2x与双曲线y=的交点均关于原点对称,
所以另一个交点坐标为(﹣2,﹣4).
15.解:∵三角形底边上的高是6,底边长为x,
∴三角形的面积y=×6 x=3x,即y=3x,
故答案为:y=3x.
16.解:3x﹣y=7中,变量是x和y,常量是3和﹣7.把它写成用x的式子表示y的形式是y=3x﹣7.
故答案是:x和y;3和﹣7;y=3x﹣7.
17.解:由题意得:|m|﹣2=﹣1且,m﹣1≠0;
解得m=±1,又m≠1;
∴m=﹣1.
故填m=﹣1.
18.解:当x=﹣2时,则y=﹣=3.
故答案为:3.
19.解:∵反比例函数y=的图象有一支在第二象限,
∴k+5<0,
解得k<﹣5.
故答案为:k<﹣5.
20.解:在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是t,
故答案为:t.
三.解答题
21.解:(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
22.解:∵反比例函数y=(3m﹣1)的图象在第二、四象限,
∴m2﹣2=﹣1,3m﹣1<0,
∴m=﹣1.
23.解:(1)自变量是时间,因变量是体温;
(2)护士每隔6小时给病人量一次体温;
(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(4)他在4月8日12时的体温是37.5摄氏度;
(5)图中的横虚线表示人的正常体温;
故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.
24.解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
25.解:问题1:①y=(﹣x)2+1=x2+1,
∴①是偶函数;
②y==﹣,
∴②是奇函数;
③y=≠≠﹣,
∴③既不是奇函数,也不是偶函数;
④y=﹣x+=﹣(x+),
∴④是奇函数;
⑤y=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|,
∴⑤是偶函数,
故答案为:奇函数有②④;偶函数有①⑤;
问题2:证明:④∵当x≠0时,
f(﹣x)=﹣x+=﹣(x+)=﹣f(x),
∴y=x+是奇函数,
⑤∵f(﹣x)=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|=f(x)(x≠0),
∴y=x﹣2﹣2|x|是偶函数.
26.解:(1)由题意得
y甲=30×4+5×(x﹣4)=100+5x(x≥4),
y乙=30×4×0.9+5x×0.9=4.5x+108(x≥4);
(2)当y甲=y乙时,即100+5x=4.5x+108,
解得x=16,
所以当购买16盒乒乓球时,到两店价格一样.
27.解:(1)设反比例函数的表达式为y=,把x=﹣1,y=2代入得k=﹣2,y=﹣.
(2)将y=代入得:x=﹣3;
将x=﹣2代入得:y=1;
将x=﹣代入得:y=4;
将x=代入得:y=﹣4,
将x=1代入得:y=﹣2;
将y=﹣1代入得:x=2,
将x=3代入得:y=﹣.
故答案为:﹣3;1;4;﹣4;﹣2;2;.
