2021-2022学年青岛版七年级下册数学第8章角 单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版七年级下册数学第8章角 单元测试卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 11:22:58 | ||
图片预览

文档简介
2021-2022学年青岛新版七年级下册数学《第8章 角》单元测试卷
一.选择题
1.下列角中,能用∠1,∠ACB,∠C三种方法表示同一个角的是( )
A. B.
C. D.
2.如图所示,用量角器度量∠MON,可以读出∠MON的度数为( )
A.60° B.70° C.110° D.115°
3.钟表盘上指示的时间是10时40分,此刻时针与分针之间的夹角为( )
A.60° B.70° C.80° D.85°
4.如图,射线OA的方向是北偏东30°,若∠AOB=90°,则射线OB的方向是( )
A.北偏西30° B.北偏西60° C.东偏北30° D.东偏北60°
5.如图,用三角板比较∠A与∠B的大小,其中正确的是( )
A.∠A>∠B B.∠A<∠B
C.∠A=∠B D.没有量角器,无法确定
6.若∠α=5.12°,则∠α用度、分、秒表示为( )
A.5°12′ B.5°7′12″ C.5°7′2″ D.5°10′2″
7.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )
A. B.
C. D.
8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )
A.∠α=∠β B.∠α>∠β C.∠α<∠β D.以上都不对
9.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=25°35′,∠BOA度数是( )
A.64°65′ B.54°65′ C.64°25′ D.54°25′
10.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°40′,则∠2的度数是( )
A.27°40′ B.62°20′ C.57°40′ D.58°20
二.填空题
11.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,若∠ACB=85°,则C处在B处的北偏东 度方向.
12.52°45′﹣32°46′= ° ′.
13.如图,锐角的个数共有 个.
14.钟面上8点30分时,时针与分针的夹角的度数是 .
15.如图,AOB为一直线,OC,OD,OE是射线,则图中大于0°小于180°的角有 个.
16.计算:23.5°+12°30′= °.
17.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为 .
18.如图,在∠AOE的内部从O引出3条射线,那么图中共有 个角;如果引出5条射线,有 个角;如果引出n条射线,有 个角.
19.图中一共有 个角.
20.比较大小:直角 锐角;38.51° 38°50′1″.
三.解答题
21.如图,在钟面上,点O为钟面的圆心,以点O为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
(1)在图1中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图2中画一个直角,使直角的内部含有3个数字,且数字之积等于数字之和;
(3)在图3中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图4中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图5中画两个直角,使这两个直角的内部含有的3个数字之和相等.
22.如图,射线OC的端点O在直线AB上,∠AOC的度数比∠BOC的3倍多20°,求∠BOC的度数是多少?
23.雨后初晴,小方同几个伙伴八点多上山采蘑菇,临出门他一看钟,时针与分针正好是重合的,下午两点多他回到家里,一进门看钟的时针与分针方向相反,正好成一条直线,问小方采蘑菇是几点去,几点回到家的,共用了多少时间?
24.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
25.把一副三角尺如图所示拼在一起.
(1)写出图中∠A、∠B、∠BCD、∠D、∠AED的度数;
(2)用小于号“<”将上述各角连接起来.
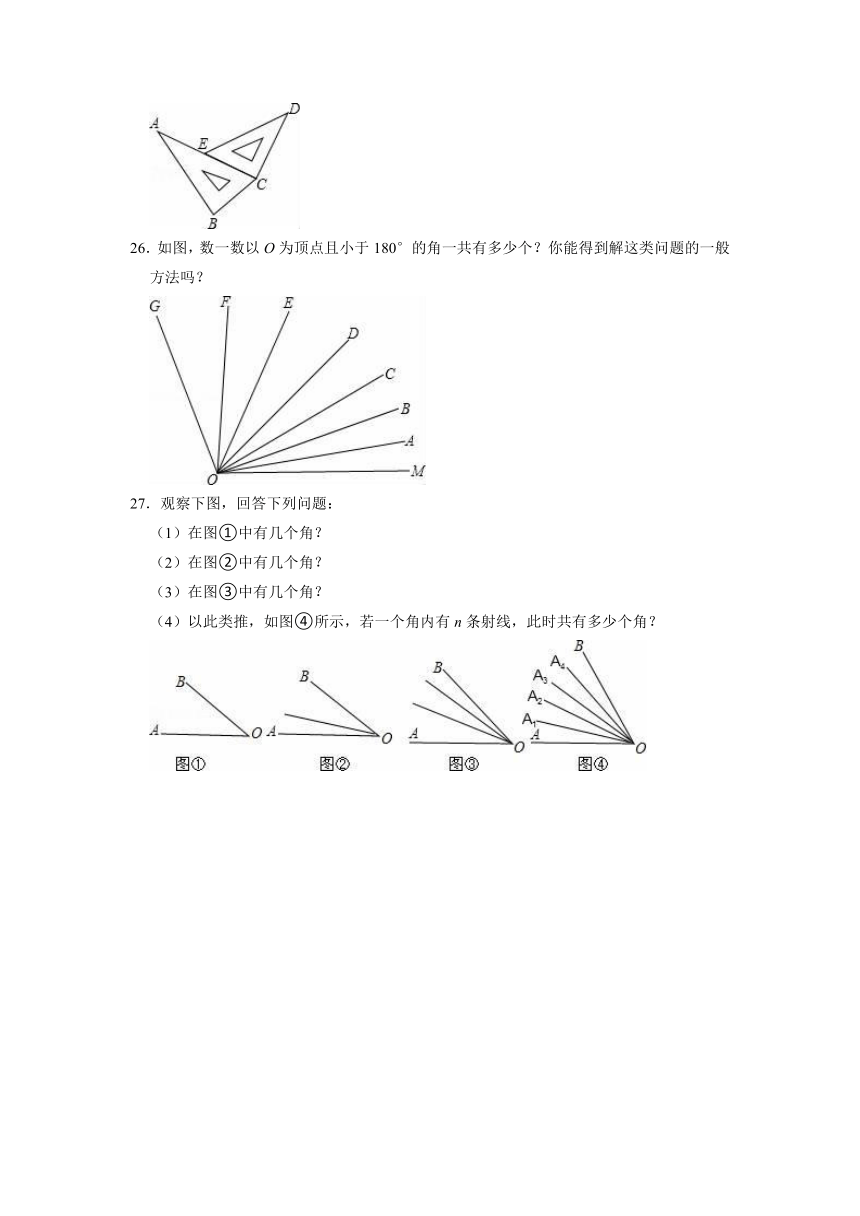
26.如图,数一数以O为顶点且小于180°的角一共有多少个?你能得到解这类问题的一般方法吗?
27.观察下图,回答下列问题:
(1)在图①中有几个角?
(2)在图②中有几个角?
(3)在图③中有几个角?
(4)以此类推,如图④所示,若一个角内有n条射线,此时共有多少个角?
参考答案与试题解析
一.选择题
1.解:在选项A、B、D中,如果用∠C表示,容易使人产生歧义,无法让人明确到底表示哪个角;
只有选项C能用∠1,∠ACB,∠C三种方法表示同一个角,不会使人产生歧义.
故选:C.
2.解:由图形所示,∠MON的度数为70°,
故选:B.
3.解:10×30+40×0.5﹣6×40
=320﹣240
=80(°),
故选:C.
4.解:如图
所示:∵OA是北偏东30°方向的一条射线,∠AOB=90°,
∴∠1=90°﹣30°=60°,
∴OB的方向角是北偏西60°.
故选:B.
5.解:由图可得,∠A<45°,∠B>45°,
∴∠A<∠B,
故选:B.
6.解:∠α=5.12°=5°+0.12×60′=5°+7′+0.2×60″=5°7′12″.
故选:B.
7.解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项错误;
B、以O为顶点的角不止一个,不能用∠O表示,故B选项错误;
C、以O为顶点的角不止一个,不能用∠O表示,故C选项错误;
D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项正确.
故选:D.
8.解:∵∠α=40.4°=40°24′,∠β=40°4′,
∴∠α>∠β.
故选:B.
9.解:∵OC平分∠DOB,
∴∠BOC=∠DOC=25°35′,
∵∠AOC=90°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣25°35′=64°25′.
故选:C.
10.解:∵∠BAC=60°,∠1=27°40′,
∴∠EAC=32°20′,
∵∠EAD=90°,
∴∠2=90°﹣∠EAC=90°﹣32°20′=57°40′;
故选:C.
二.填空题
11.解:∵B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,
∴∠BAC=45°+15°=60°,
∵∠ACB=85°,
∴∠ABC=180°﹣60°﹣85°=35°,
∴C处在B处的北偏东45°+35°=80°,
故答案为80.
12.解:52°45′﹣32°46′=19° 59′.
故答案为:19,59.
13.解:以OA为一边的角∠AOB=20°,∠AOC=20°+30°=50°,∠AOD=20°+30°+50°=100°(钝角舍去),
以OB为一边的角∠BOC=30°,∠BOD=50°+30°=80°,
以OC为一边的角∠COD=50°.
共有∠AOB,∠AOC,∠BOC,∠BOD,∠COD.
故答案为5个.
14.解:∵8点30分,时针在8和9正中间,分针指向6,中间相差两个半大格,而钟表12个数字,每相邻两个数字之间的夹角为30°,
∴8点30分时,时针与分针的夹角的度数为:30°×2.5=75°.
故答案为:75°.
15.解:大于0°小于180°的角有
∠AOE,∠AOD,∠AOC,∠EOD,∠EOC,∠EOB,∠DOC,∠DOB,∠COB.
共9个.
故答案为:9.
16.解:23.5°+12°30′=23.5°+12.5°=36°.
故答案为:36.
17.解:∵∠AOB=90°,∠BOE=30°,
∴∠AOE=90°﹣30°=60°,
∵OE平分∠AOC,
∴∠COE=∠AOE=60°,
∴∠BOC=60°﹣30°=30°,
∵OD平分∠BOC,
∴∠BOD=∠BOC=15°,
∴∠DOE=∠BOD+∠BOE=45°;
故答案为:45°.
18.解:引出3条射线,那么图中共有10个角;如果引出5条射线,有21个角;如果引出n条射线,有(n+1)(n+2)个角.
19.解:图中的角有:∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD这6个,
故答案为:6.
20.解:直角=90°,锐角大于0°而小于90度.
故直角>锐角;38.51°=38°30′36″<38°50′1″.
三.解答题
21.解:如图所示,(1)如图1,∠AOB即为所求;
(2)如图2,∠AOB即为所求;
(3)如图3,∠COD即为所求;
(4)如图4,∠DOE即为所求;
(5)如图5,∠EOF和∠MON即为所求.
22.解:设∠BOC=x°,则∠AOC=(3x+20)°,
∠AOB=∠AOC+∠BOC=x°+(3x+20)°=(4x+20)°=180°,
解得x=40,
答:∠BOC的度数是40°
23.解:设8点x分时针与分针重合,则
所以:x﹣=40,解得:x=43.
即8点43分时出门.
设14点y分时,时针与分针方向相反.
所以:y﹣=10+30,解得:y=43.
即14点43分时回家
所以14点43分﹣8点43=6小时.
故共用了6小时.
24.解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
25.解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;
(2)∠A<∠D<∠B<∠AED<∠BCD.
26.解:7+6+5+4+3+2+1==28,
一般地如果MOG小于180,且图中一共有几条射线,
则一共有:(n﹣1)+(n﹣2)+…+2+1=.
27.解:由分析知:
(1)①图中有2条射线,则角的个数为:=1(个);
(2)②图中有3条射线,则角的个数为:=3(个);
(3)③图中有4条射线,则角的个数为:=6(个);
(4)由前三问类推,角内有n条射线时,图中共有(n+2)条射线,则角的个数为个.
一.选择题
1.下列角中,能用∠1,∠ACB,∠C三种方法表示同一个角的是( )
A. B.
C. D.
2.如图所示,用量角器度量∠MON,可以读出∠MON的度数为( )
A.60° B.70° C.110° D.115°
3.钟表盘上指示的时间是10时40分,此刻时针与分针之间的夹角为( )
A.60° B.70° C.80° D.85°
4.如图,射线OA的方向是北偏东30°,若∠AOB=90°,则射线OB的方向是( )
A.北偏西30° B.北偏西60° C.东偏北30° D.东偏北60°
5.如图,用三角板比较∠A与∠B的大小,其中正确的是( )
A.∠A>∠B B.∠A<∠B
C.∠A=∠B D.没有量角器,无法确定
6.若∠α=5.12°,则∠α用度、分、秒表示为( )
A.5°12′ B.5°7′12″ C.5°7′2″ D.5°10′2″
7.如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形的是( )
A. B.
C. D.
8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )
A.∠α=∠β B.∠α>∠β C.∠α<∠β D.以上都不对
9.如图,∠AOC=90°,OC平分∠DOB,且∠DOC=25°35′,∠BOA度数是( )
A.64°65′ B.54°65′ C.64°25′ D.54°25′
10.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1=27°40′,则∠2的度数是( )
A.27°40′ B.62°20′ C.57°40′ D.58°20
二.填空题
11.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,若∠ACB=85°,则C处在B处的北偏东 度方向.
12.52°45′﹣32°46′= ° ′.
13.如图,锐角的个数共有 个.
14.钟面上8点30分时,时针与分针的夹角的度数是 .
15.如图,AOB为一直线,OC,OD,OE是射线,则图中大于0°小于180°的角有 个.
16.计算:23.5°+12°30′= °.
17.如图,∠AOB=90°,OD,OE分别是∠BOC和∠AOC的平分线,若∠BOE=30°,则∠DOE的度数为 .
18.如图,在∠AOE的内部从O引出3条射线,那么图中共有 个角;如果引出5条射线,有 个角;如果引出n条射线,有 个角.
19.图中一共有 个角.
20.比较大小:直角 锐角;38.51° 38°50′1″.
三.解答题
21.如图,在钟面上,点O为钟面的圆心,以点O为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
(1)在图1中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图2中画一个直角,使直角的内部含有3个数字,且数字之积等于数字之和;
(3)在图3中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图4中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图5中画两个直角,使这两个直角的内部含有的3个数字之和相等.
22.如图,射线OC的端点O在直线AB上,∠AOC的度数比∠BOC的3倍多20°,求∠BOC的度数是多少?
23.雨后初晴,小方同几个伙伴八点多上山采蘑菇,临出门他一看钟,时针与分针正好是重合的,下午两点多他回到家里,一进门看钟的时针与分针方向相反,正好成一条直线,问小方采蘑菇是几点去,几点回到家的,共用了多少时间?
24.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
25.把一副三角尺如图所示拼在一起.
(1)写出图中∠A、∠B、∠BCD、∠D、∠AED的度数;
(2)用小于号“<”将上述各角连接起来.
26.如图,数一数以O为顶点且小于180°的角一共有多少个?你能得到解这类问题的一般方法吗?
27.观察下图,回答下列问题:
(1)在图①中有几个角?
(2)在图②中有几个角?
(3)在图③中有几个角?
(4)以此类推,如图④所示,若一个角内有n条射线,此时共有多少个角?
参考答案与试题解析
一.选择题
1.解:在选项A、B、D中,如果用∠C表示,容易使人产生歧义,无法让人明确到底表示哪个角;
只有选项C能用∠1,∠ACB,∠C三种方法表示同一个角,不会使人产生歧义.
故选:C.
2.解:由图形所示,∠MON的度数为70°,
故选:B.
3.解:10×30+40×0.5﹣6×40
=320﹣240
=80(°),
故选:C.
4.解:如图
所示:∵OA是北偏东30°方向的一条射线,∠AOB=90°,
∴∠1=90°﹣30°=60°,
∴OB的方向角是北偏西60°.
故选:B.
5.解:由图可得,∠A<45°,∠B>45°,
∴∠A<∠B,
故选:B.
6.解:∠α=5.12°=5°+0.12×60′=5°+7′+0.2×60″=5°7′12″.
故选:B.
7.解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项错误;
B、以O为顶点的角不止一个,不能用∠O表示,故B选项错误;
C、以O为顶点的角不止一个,不能用∠O表示,故C选项错误;
D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项正确.
故选:D.
8.解:∵∠α=40.4°=40°24′,∠β=40°4′,
∴∠α>∠β.
故选:B.
9.解:∵OC平分∠DOB,
∴∠BOC=∠DOC=25°35′,
∵∠AOC=90°,
∴∠AOB=∠AOC﹣∠BOC=90°﹣25°35′=64°25′.
故选:C.
10.解:∵∠BAC=60°,∠1=27°40′,
∴∠EAC=32°20′,
∵∠EAD=90°,
∴∠2=90°﹣∠EAC=90°﹣32°20′=57°40′;
故选:C.
二.填空题
11.解:∵B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,
∴∠BAC=45°+15°=60°,
∵∠ACB=85°,
∴∠ABC=180°﹣60°﹣85°=35°,
∴C处在B处的北偏东45°+35°=80°,
故答案为80.
12.解:52°45′﹣32°46′=19° 59′.
故答案为:19,59.
13.解:以OA为一边的角∠AOB=20°,∠AOC=20°+30°=50°,∠AOD=20°+30°+50°=100°(钝角舍去),
以OB为一边的角∠BOC=30°,∠BOD=50°+30°=80°,
以OC为一边的角∠COD=50°.
共有∠AOB,∠AOC,∠BOC,∠BOD,∠COD.
故答案为5个.
14.解:∵8点30分,时针在8和9正中间,分针指向6,中间相差两个半大格,而钟表12个数字,每相邻两个数字之间的夹角为30°,
∴8点30分时,时针与分针的夹角的度数为:30°×2.5=75°.
故答案为:75°.
15.解:大于0°小于180°的角有
∠AOE,∠AOD,∠AOC,∠EOD,∠EOC,∠EOB,∠DOC,∠DOB,∠COB.
共9个.
故答案为:9.
16.解:23.5°+12°30′=23.5°+12.5°=36°.
故答案为:36.
17.解:∵∠AOB=90°,∠BOE=30°,
∴∠AOE=90°﹣30°=60°,
∵OE平分∠AOC,
∴∠COE=∠AOE=60°,
∴∠BOC=60°﹣30°=30°,
∵OD平分∠BOC,
∴∠BOD=∠BOC=15°,
∴∠DOE=∠BOD+∠BOE=45°;
故答案为:45°.
18.解:引出3条射线,那么图中共有10个角;如果引出5条射线,有21个角;如果引出n条射线,有(n+1)(n+2)个角.
19.解:图中的角有:∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD这6个,
故答案为:6.
20.解:直角=90°,锐角大于0°而小于90度.
故直角>锐角;38.51°=38°30′36″<38°50′1″.
三.解答题
21.解:如图所示,(1)如图1,∠AOB即为所求;
(2)如图2,∠AOB即为所求;
(3)如图3,∠COD即为所求;
(4)如图4,∠DOE即为所求;
(5)如图5,∠EOF和∠MON即为所求.
22.解:设∠BOC=x°,则∠AOC=(3x+20)°,
∠AOB=∠AOC+∠BOC=x°+(3x+20)°=(4x+20)°=180°,
解得x=40,
答:∠BOC的度数是40°
23.解:设8点x分时针与分针重合,则
所以:x﹣=40,解得:x=43.
即8点43分时出门.
设14点y分时,时针与分针方向相反.
所以:y﹣=10+30,解得:y=43.
即14点43分时回家
所以14点43分﹣8点43=6小时.
故共用了6小时.
24.解:(1)∵OB的方向是北偏西40°,OA的方向是北偏东15°,
∴∠NOB=40°,∠NOA=15°,
∴∠AOB=∠NOB+∠NOA=55°,
∵∠AOB=∠AOC,
∴∠AOC=55°,
∴∠NOC=∠NOA+∠AOC=70°,
∴OC的方向是北偏东70°;
故答案为:北偏东70°;
(2)∵∠AOB=55°,∠AOC=∠AOB,
∴∠BOC=110°.
又∵射线OD是OB的反向延长线,
∴∠BOD=180°.
∴∠COD=180°﹣110°=70°.
∵∠COD=70°,OE平分∠COD,
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°.
25.解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;
(2)∠A<∠D<∠B<∠AED<∠BCD.
26.解:7+6+5+4+3+2+1==28,
一般地如果MOG小于180,且图中一共有几条射线,
则一共有:(n﹣1)+(n﹣2)+…+2+1=.
27.解:由分析知:
(1)①图中有2条射线,则角的个数为:=1(个);
(2)②图中有3条射线,则角的个数为:=3(个);
(3)③图中有4条射线,则角的个数为:=6(个);
(4)由前三问类推,角内有n条射线时,图中共有(n+2)条射线,则角的个数为个.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
