2021-2022学年冀教版九年级数学下册第30章 二次函数 单元测试卷 (word版无答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册第30章 二次函数 单元测试卷 (word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 96.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 11:36:08 | ||
图片预览

文档简介
第30章 二次函数 单元测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 二次函数的对称轴是( )
A.直线 B.直线 C.轴 D.轴
2. 函数是二次函数,则的值为( )
A. B. C. D.
3. 二次函数的顶点为
A. B. C. D.
4. 对于二次函数,当自变量满足时,函数值的取值范围为,则的取值范围为
A. B. C. D.
5. 抛物线的顶点坐标是 ( )
A. B. C. D.
6. 已知抛物线经过点,且满足,有下列结论:①;②;③.其中,正确结论的个数是( )
A. B. C. D.
7. 若抛物线与轴两个交点间的距离为,已知该抛物线的对称轴为直线,将此抛物线向左平移个单位,再向下平移个单位,得到的抛物线过点( )
A. B. C. D.
8. 抛物线上部分点的横坐标,纵坐标的对应值如下表:
… …
… …
现给出下列结论:
抛物线与轴的一个交点为 ;函数的最大值为;
抛物线的对称轴是直线; 在对称轴左侧,随增大而增大;
方程有两个不相等实数根.
其中正确的结论是( )
A. B. C. D.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
9. 二次函数=的最大值是________.
10. 将抛物线:向上平移个单位,再向右平移个单位得到的抛物线是________.
11. 抛物线经过点,则抛物线解析式为________.
12. 如果一个圆的半径为,面积为,那么关于的函数解析式是________.
13. 把二次函数化成的形式是________.
14. 如果抛物线的顶点到轴的距离是,则的值等于________.
15. 某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润(单位:万元)与销售量(单位:辆)之间分别满足:,,若该公司在甲,乙两地共销售辆该品牌的汽车,则能获得的最大利润为________ 万元.
16. 若函数的图象与轴只有一个公共点,则________.
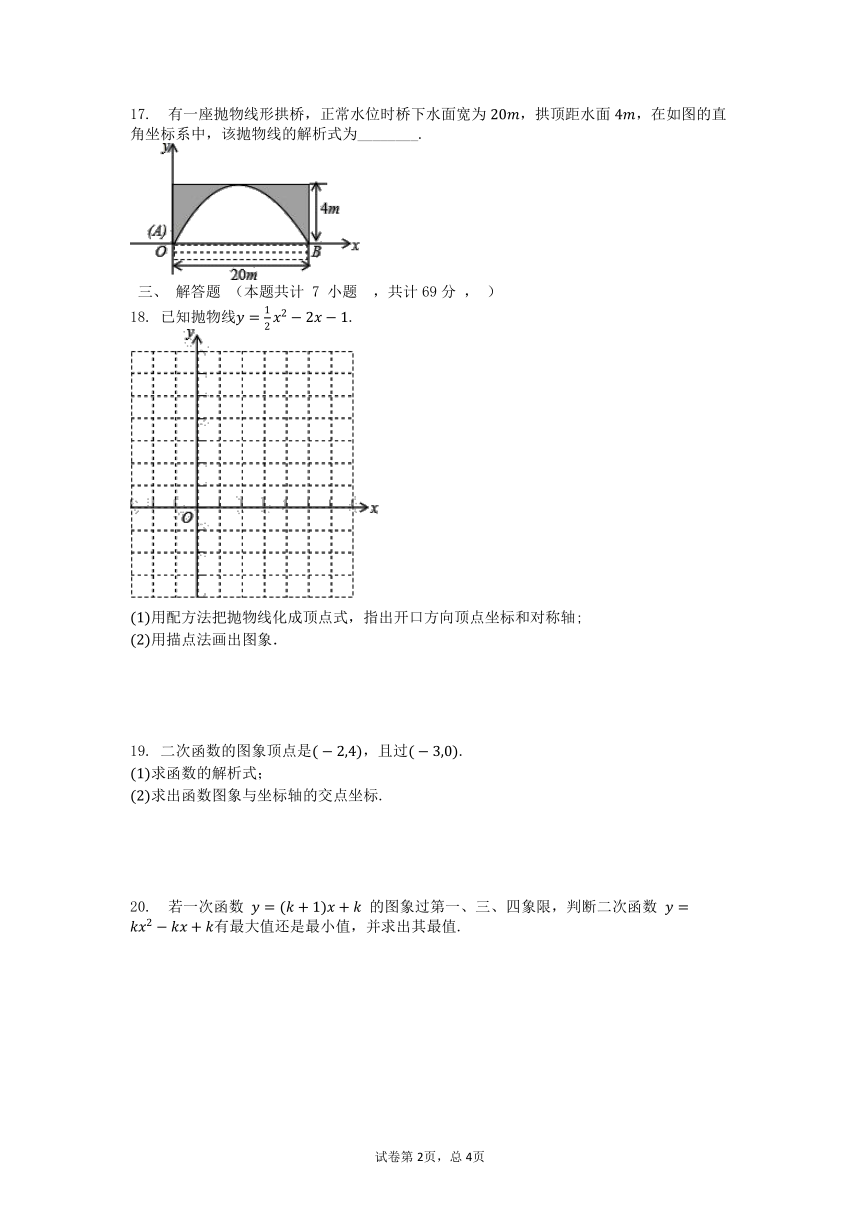
17. 有一座抛物线形拱桥,正常水位时桥下水面宽为,拱顶距水面,在如图的直角坐标系中,该抛物线的解析式为________.
三、 解答题 (本题共计 7 小题 ,共计69分 , )
18. 已知抛物线.
用配方法把抛物线化成顶点式,指出开口方向顶点坐标和对称轴;
用描点法画出图象.
19. 二次函数的图象顶点是,且过.
求函数的解析式;
求出函数图象与坐标轴的交点坐标.
20. 若一次函数 的图象过第一、三、四象限,判断二次函数 有最大值还是最小值,并求出其最值.
21. 某企业接到一批粽子生产任务,按要求在天内完成,约定这批粽子的出厂价为每只元.为按时完成任务,该企业招收了新工人.设新工人李明第天生产的粽子数量为只,与满足如下关系:
李明第几天生产的粽子数量为只?
如图,设第天每只粽子的成本是元,与之间的关系可用图中的函数图形来刻画.若李明第天创造的利润为元,求关于的函数表达式,并求出第几天的利润最大,最大利润时多少元?(利润出厂价-成本)
22. 已知二次函数=.
(1)若函数图象经过点,,求,的值;
(2)证明:若=,则存在一条确定的直线始终与该函数图象交于两点.
23. 二次函数的图象交轴于点,点两点,交轴于点,动点从点出发,以每秒个单位长度的速度沿方向运动,过点作轴交直线于点,交抛物线于点,连接,设运动时间为秒.
求二次函数的表达式;
直线上存在一点,当是以为直角的等腰—直角三角形时,求此时点的坐标;
24. 已知二次函数.
完成下表,并在平面直角坐标系中画出这个函数图象.
结合图象回答:
①当时,随的增大而________;(填“增大”或“减小”)
②不等式的解集是________.试卷第2页,总2页
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 二次函数的对称轴是( )
A.直线 B.直线 C.轴 D.轴
2. 函数是二次函数,则的值为( )
A. B. C. D.
3. 二次函数的顶点为
A. B. C. D.
4. 对于二次函数,当自变量满足时,函数值的取值范围为,则的取值范围为
A. B. C. D.
5. 抛物线的顶点坐标是 ( )
A. B. C. D.
6. 已知抛物线经过点,且满足,有下列结论:①;②;③.其中,正确结论的个数是( )
A. B. C. D.
7. 若抛物线与轴两个交点间的距离为,已知该抛物线的对称轴为直线,将此抛物线向左平移个单位,再向下平移个单位,得到的抛物线过点( )
A. B. C. D.
8. 抛物线上部分点的横坐标,纵坐标的对应值如下表:
… …
… …
现给出下列结论:
抛物线与轴的一个交点为 ;函数的最大值为;
抛物线的对称轴是直线; 在对称轴左侧,随增大而增大;
方程有两个不相等实数根.
其中正确的结论是( )
A. B. C. D.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
9. 二次函数=的最大值是________.
10. 将抛物线:向上平移个单位,再向右平移个单位得到的抛物线是________.
11. 抛物线经过点,则抛物线解析式为________.
12. 如果一个圆的半径为,面积为,那么关于的函数解析式是________.
13. 把二次函数化成的形式是________.
14. 如果抛物线的顶点到轴的距离是,则的值等于________.
15. 某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润(单位:万元)与销售量(单位:辆)之间分别满足:,,若该公司在甲,乙两地共销售辆该品牌的汽车,则能获得的最大利润为________ 万元.
16. 若函数的图象与轴只有一个公共点,则________.
17. 有一座抛物线形拱桥,正常水位时桥下水面宽为,拱顶距水面,在如图的直角坐标系中,该抛物线的解析式为________.
三、 解答题 (本题共计 7 小题 ,共计69分 , )
18. 已知抛物线.
用配方法把抛物线化成顶点式,指出开口方向顶点坐标和对称轴;
用描点法画出图象.
19. 二次函数的图象顶点是,且过.
求函数的解析式;
求出函数图象与坐标轴的交点坐标.
20. 若一次函数 的图象过第一、三、四象限,判断二次函数 有最大值还是最小值,并求出其最值.
21. 某企业接到一批粽子生产任务,按要求在天内完成,约定这批粽子的出厂价为每只元.为按时完成任务,该企业招收了新工人.设新工人李明第天生产的粽子数量为只,与满足如下关系:
李明第几天生产的粽子数量为只?
如图,设第天每只粽子的成本是元,与之间的关系可用图中的函数图形来刻画.若李明第天创造的利润为元,求关于的函数表达式,并求出第几天的利润最大,最大利润时多少元?(利润出厂价-成本)
22. 已知二次函数=.
(1)若函数图象经过点,,求,的值;
(2)证明:若=,则存在一条确定的直线始终与该函数图象交于两点.
23. 二次函数的图象交轴于点,点两点,交轴于点,动点从点出发,以每秒个单位长度的速度沿方向运动,过点作轴交直线于点,交抛物线于点,连接,设运动时间为秒.
求二次函数的表达式;
直线上存在一点,当是以为直角的等腰—直角三角形时,求此时点的坐标;
24. 已知二次函数.
完成下表,并在平面直角坐标系中画出这个函数图象.
结合图象回答:
①当时,随的增大而________;(填“增大”或“减小”)
②不等式的解集是________.试卷第2页,总2页
