北师大版2021-2022年初中数学九年级下册3.5确定圆的条件课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学九年级下册3.5确定圆的条件课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 547.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 01:11:06 | ||
图片预览



文档简介
2021-2022年初中数学九年级下册同步(北师大版)
3.5确定圆的条件-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③三角形的外心是各边垂直平分线的交点;④三角形的外心到三角形三边的距离相等;⑤等腰三角形的外心一定在这个三角形内,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,坐标平面上有,,点,其中,若,则的外心在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知⊙O是△ABC的外接圆,若AB=AC=5,BC=6,则⊙O的半径为( )
A.4 B.3.25 C.3.125 D.2.25
4.如图,为锐角三角形的外心,四边形为正方形,其中点在的外部,判断下列叙述正确的是( )
A.是的外心,是的外心 B.是的外心,不是的外心
C.不是的外心,是的外心 D.不是的外心,不是的外心
5.用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,作法错误的是( )
A. B.
C. D.
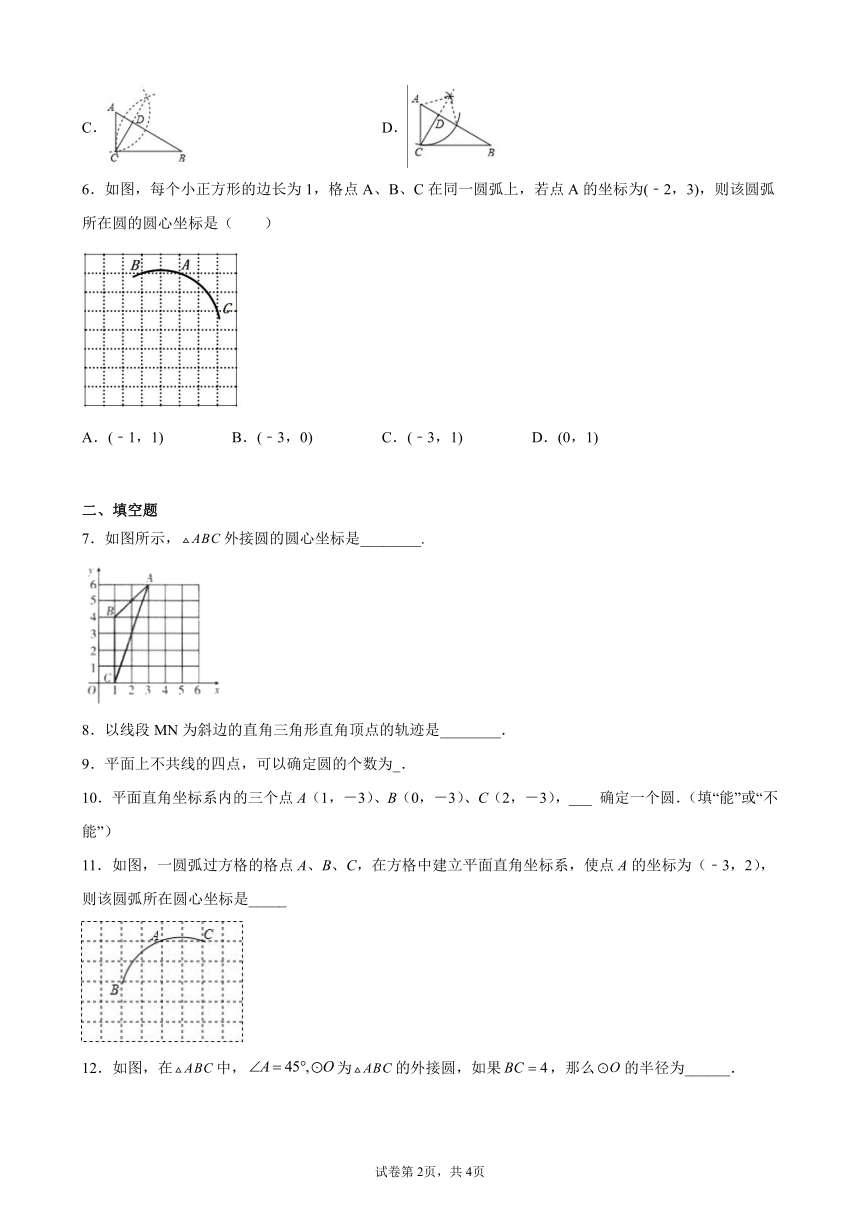
6.如图,每个小正方形的边长为1,格点A、B、C在同一圆弧上,若点A的坐标为(﹣2,3),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,1) B.(﹣3,0) C.(﹣3,1) D.(0,1)
二、填空题
7.如图所示,外接圆的圆心坐标是________.
8.以线段MN为斜边的直角三角形直角顶点的轨迹是________.
9.平面上不共线的四点,可以确定圆的个数为_.
10.平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3),___ 确定一个圆.(填“能”或“不能”)
11.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____
12.如图,在中,为的外接圆,如果,那么的半径为______.
三、解答题
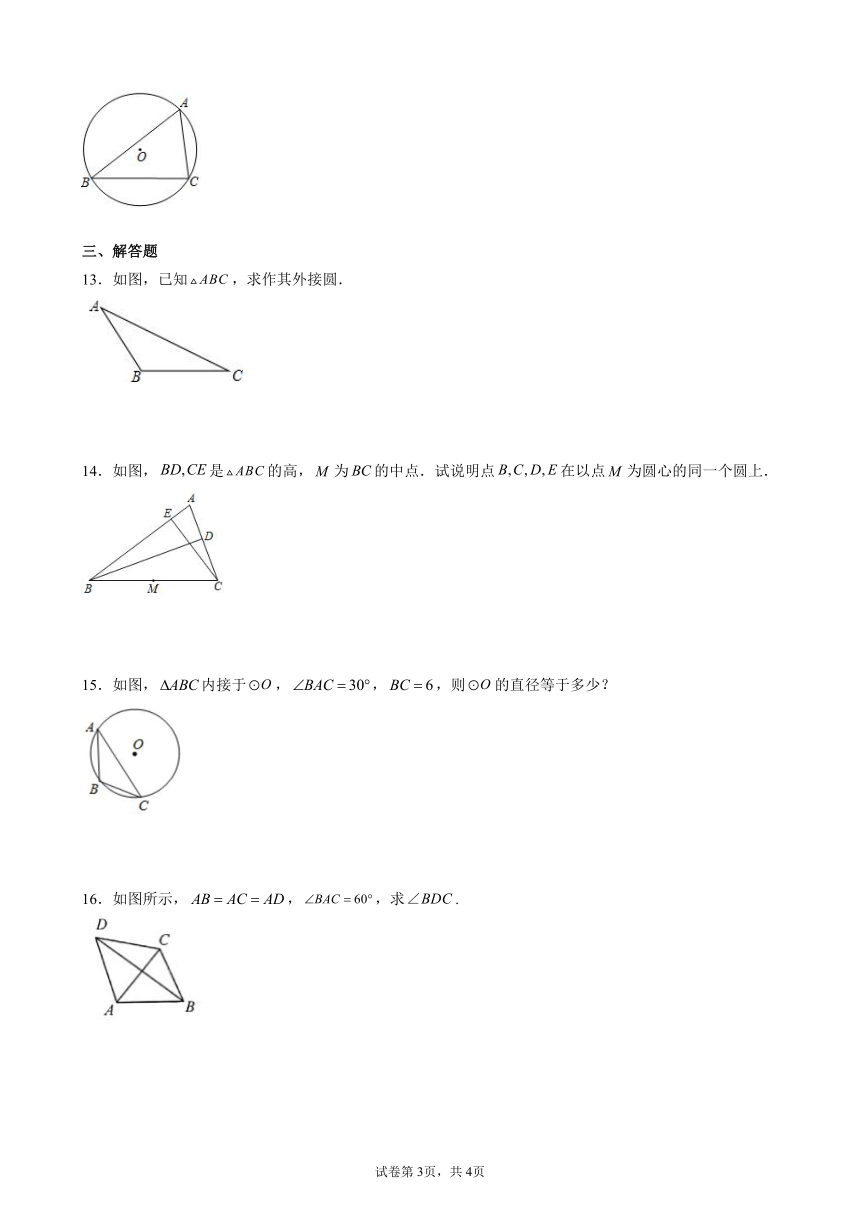
13.如图,已知,求作其外接圆.
14.如图,是的高,为的中点.试说明点在以点为圆心的同一个圆上.
15.如图,内接于,,,则的直径等于多少?
16.如图所示,,,求.
17.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
18.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
参考答案
1.B
【解析】解:②③正确;不在同一直线上的三点确定一个圆,所以①错误;三角形的外心到三角形三个顶点的距离相等,所以④错误;当等腰三角形是钝角三角形时,它的外心在这个三角形外;当等腰三角形是直角三角形时,它的外心在这个三角形的斜边上,所以⑤错误,
∴正确的有②③,
故选:B.
2.D
【解析】解析:∵点,点,
∴的外心在直线上.
∵,
∴的外心在三角形的外部,
∴的外心在第四象限,
故选:D.
3.C
【解析】
过A作AD⊥BC于D,
△ABC中,AB=AC,AD⊥BC,
则AD必过圆心O,
Rt△ABD中,AB=5,BD=3
∴AD=4
设⊙O的半径为x,
Rt△OBD中,OB=x,OD=4-x
根据勾股定理,得:OB2=OD2+BD2,即:
x2=(4-x)2+32,解得:x==3.125.
故选C.
4.B
【解析】解析:如图,连接,,,
∵是的外心,
∴,
∵四边形是正方形,
∴,
∴是的外心,
∵,
∴不是的外心,
故选:B.
5.D
【解析】A、由图示可知应用了垂径定理作图的方法,所以CD是Rt△ABC斜边AB上的高线,不符合题意; B、由直径所对的圆周角是直角可知∠BDC=90°,所以CD是Rt△ABC斜边AB上的高线,不符合题意; C、根据相交两圆的公共弦被连接两圆的连心线垂直平分可知,CD是Rt△ABC斜边AB上的高线,不符合题意; D、无法证明CD是Rt△ABC斜边AB上的高线,符合题意.故选D.
6.B
【解析】如图所示,
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
∵点A的坐标为(-2,3),
∴该圆弧所在圆的圆心坐标是(-3,0).
故选:B.
7.
【解析】解:作AB和BC的垂直平分线,它们的交点P为△ABC外接圆圆心,
∵ P点坐标是P(5,2),
∴ 外接圆的圆心坐标是(5,2).
故答案为(5,2).
8.以MN为直径圆(除M、N两点外)
【解析】根据直角三角形的性质,斜边即为外接圆的直径,
故以线段MN为斜边的直角三角形直角顶点的轨迹是以线段MN中点为圆心,MN为直径的圆(不包含M、N两点).
故答案为:以MN为直径圆(除M、N两点外).
9.1个或3个或4个
【解析】解:(1)当四个点中有三个点在同一直线上,另外一个点不在这条直线上时,确定3个圆;
(2)当四个点中任意三个点都不在同一条直线上,并且四点不共圆时,则任意三点都能确定一个圆,一共确定4个圆;
(3)当四个点共圆时,只能确定一个圆.
故答案为:1个或3个或4个.
10.不能
【解析】解:∵B(0,-3)、C(2,-3),
∴BC∥x轴,
而点A(1,-3)与C、B共线,
∴点A、B、C共线,
∴三个点A(1,-3)、B(0,-3)、C(2,-3)不能确定一个圆.
故答案为:不能.
11.(﹣2,﹣1)
【解析】如图:分别作AC与AB的垂直平分线,相交于点O,
则点O即是该圆弧所在圆的圆心.
∵点A的坐标为(﹣3,2),∴点O的坐标为(﹣2,﹣1).
12.
【解析】解:连接、,作,
,
,
又∵OB=OC,,,
,
∴在中,,
故答案为:.
13.见解析
【解析】解:如图,⊙O为所求.
14.见解析
【解析】证明:连接,.
分别是的高,为的中点,
,
∴点在以点为圆心的同一圆上.
15.12
【解析】解:连接OB、OC,如图,
∵∠BOC=2∠BAC=2×30°=60°,
而OB=OC,
∴△OBC为等边三角形,
∴OB=BC=6,
∴⊙O的直径等于12.
故答案为:12.
16.30°.
【解析】解:∵AB=AC=AD,
∴B,C,D在以A为圆心,AB为半径的圆上,
∴∠CAD=2∠CBD,∠BAC=2∠BDC,
∵∠CBD=2∠BDC,∠BAC=60°,
∴∠CAD=2∠BAC=120°.
∴∠BDC=30°.
17.(1)作图见解析;(2)圆的半径为13 cm.
【解析】解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,
以O为圆心OA长为半径作圆O就是此残片所在的圆如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:x2=122+(x-8)2,解得:x=13.
答:圆的半径为13cm.
18.(1)证明见解析(2)4
【解析】解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC.
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°.
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°.
∴△ABC是等边三角形.
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心.
∴BO平分∠ABC.∴∠OBD=30°.∴OD=8×=4.
试卷第4页,共4页
试卷第3页,共4页
3.5确定圆的条件-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③三角形的外心是各边垂直平分线的交点;④三角形的外心到三角形三边的距离相等;⑤等腰三角形的外心一定在这个三角形内,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,坐标平面上有,,点,其中,若,则的外心在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知⊙O是△ABC的外接圆,若AB=AC=5,BC=6,则⊙O的半径为( )
A.4 B.3.25 C.3.125 D.2.25
4.如图,为锐角三角形的外心,四边形为正方形,其中点在的外部,判断下列叙述正确的是( )
A.是的外心,是的外心 B.是的外心,不是的外心
C.不是的外心,是的外心 D.不是的外心,不是的外心
5.用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,作法错误的是( )
A. B.
C. D.
6.如图,每个小正方形的边长为1,格点A、B、C在同一圆弧上,若点A的坐标为(﹣2,3),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,1) B.(﹣3,0) C.(﹣3,1) D.(0,1)
二、填空题
7.如图所示,外接圆的圆心坐标是________.
8.以线段MN为斜边的直角三角形直角顶点的轨迹是________.
9.平面上不共线的四点,可以确定圆的个数为_.
10.平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3),___ 确定一个圆.(填“能”或“不能”)
11.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____
12.如图,在中,为的外接圆,如果,那么的半径为______.
三、解答题
13.如图,已知,求作其外接圆.
14.如图,是的高,为的中点.试说明点在以点为圆心的同一个圆上.
15.如图,内接于,,,则的直径等于多少?
16.如图所示,,,求.
17.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
18.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
参考答案
1.B
【解析】解:②③正确;不在同一直线上的三点确定一个圆,所以①错误;三角形的外心到三角形三个顶点的距离相等,所以④错误;当等腰三角形是钝角三角形时,它的外心在这个三角形外;当等腰三角形是直角三角形时,它的外心在这个三角形的斜边上,所以⑤错误,
∴正确的有②③,
故选:B.
2.D
【解析】解析:∵点,点,
∴的外心在直线上.
∵,
∴的外心在三角形的外部,
∴的外心在第四象限,
故选:D.
3.C
【解析】
过A作AD⊥BC于D,
△ABC中,AB=AC,AD⊥BC,
则AD必过圆心O,
Rt△ABD中,AB=5,BD=3
∴AD=4
设⊙O的半径为x,
Rt△OBD中,OB=x,OD=4-x
根据勾股定理,得:OB2=OD2+BD2,即:
x2=(4-x)2+32,解得:x==3.125.
故选C.
4.B
【解析】解析:如图,连接,,,
∵是的外心,
∴,
∵四边形是正方形,
∴,
∴是的外心,
∵,
∴不是的外心,
故选:B.
5.D
【解析】A、由图示可知应用了垂径定理作图的方法,所以CD是Rt△ABC斜边AB上的高线,不符合题意; B、由直径所对的圆周角是直角可知∠BDC=90°,所以CD是Rt△ABC斜边AB上的高线,不符合题意; C、根据相交两圆的公共弦被连接两圆的连心线垂直平分可知,CD是Rt△ABC斜边AB上的高线,不符合题意; D、无法证明CD是Rt△ABC斜边AB上的高线,符合题意.故选D.
6.B
【解析】如图所示,
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
∵点A的坐标为(-2,3),
∴该圆弧所在圆的圆心坐标是(-3,0).
故选:B.
7.
【解析】解:作AB和BC的垂直平分线,它们的交点P为△ABC外接圆圆心,
∵ P点坐标是P(5,2),
∴ 外接圆的圆心坐标是(5,2).
故答案为(5,2).
8.以MN为直径圆(除M、N两点外)
【解析】根据直角三角形的性质,斜边即为外接圆的直径,
故以线段MN为斜边的直角三角形直角顶点的轨迹是以线段MN中点为圆心,MN为直径的圆(不包含M、N两点).
故答案为:以MN为直径圆(除M、N两点外).
9.1个或3个或4个
【解析】解:(1)当四个点中有三个点在同一直线上,另外一个点不在这条直线上时,确定3个圆;
(2)当四个点中任意三个点都不在同一条直线上,并且四点不共圆时,则任意三点都能确定一个圆,一共确定4个圆;
(3)当四个点共圆时,只能确定一个圆.
故答案为:1个或3个或4个.
10.不能
【解析】解:∵B(0,-3)、C(2,-3),
∴BC∥x轴,
而点A(1,-3)与C、B共线,
∴点A、B、C共线,
∴三个点A(1,-3)、B(0,-3)、C(2,-3)不能确定一个圆.
故答案为:不能.
11.(﹣2,﹣1)
【解析】如图:分别作AC与AB的垂直平分线,相交于点O,
则点O即是该圆弧所在圆的圆心.
∵点A的坐标为(﹣3,2),∴点O的坐标为(﹣2,﹣1).
12.
【解析】解:连接、,作,
,
,
又∵OB=OC,,,
,
∴在中,,
故答案为:.
13.见解析
【解析】解:如图,⊙O为所求.
14.见解析
【解析】证明:连接,.
分别是的高,为的中点,
,
∴点在以点为圆心的同一圆上.
15.12
【解析】解:连接OB、OC,如图,
∵∠BOC=2∠BAC=2×30°=60°,
而OB=OC,
∴△OBC为等边三角形,
∴OB=BC=6,
∴⊙O的直径等于12.
故答案为:12.
16.30°.
【解析】解:∵AB=AC=AD,
∴B,C,D在以A为圆心,AB为半径的圆上,
∴∠CAD=2∠CBD,∠BAC=2∠BDC,
∵∠CBD=2∠BDC,∠BAC=60°,
∴∠CAD=2∠BAC=120°.
∴∠BDC=30°.
17.(1)作图见解析;(2)圆的半径为13 cm.
【解析】解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,
以O为圆心OA长为半径作圆O就是此残片所在的圆如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:x2=122+(x-8)2,解得:x=13.
答:圆的半径为13cm.
18.(1)证明见解析(2)4
【解析】解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC.
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°.
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°.
∴△ABC是等边三角形.
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心.
∴BO平分∠ABC.∴∠OBD=30°.∴OD=8×=4.
试卷第4页,共4页
试卷第3页,共4页
