北师大版2021-2022年初中数学九年级下册3.9弧长及扇形的面积课堂练习(Word版含答案)
文档属性
| 名称 | 北师大版2021-2022年初中数学九年级下册3.9弧长及扇形的面积课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 697.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 01:12:19 | ||
图片预览



文档简介
2021-2022年初中数学九年级下册同步(北师大版)
3.9弧长及扇形的面积-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正方形的边长,分别以点,为圆心,长为半径画弧,两弧交于点,则的长是( )
A. B. C. D.
2.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
3.在圆心角为的扇形中,半径,则扇形的面积是( )
A. B. C. D.
4.如图,在边长为4的正方形内部裁得一个扇形,若将该扇形围成一个圆锥,则此圆锥的底面半径为( )
A.1 B. C. D.2
5.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
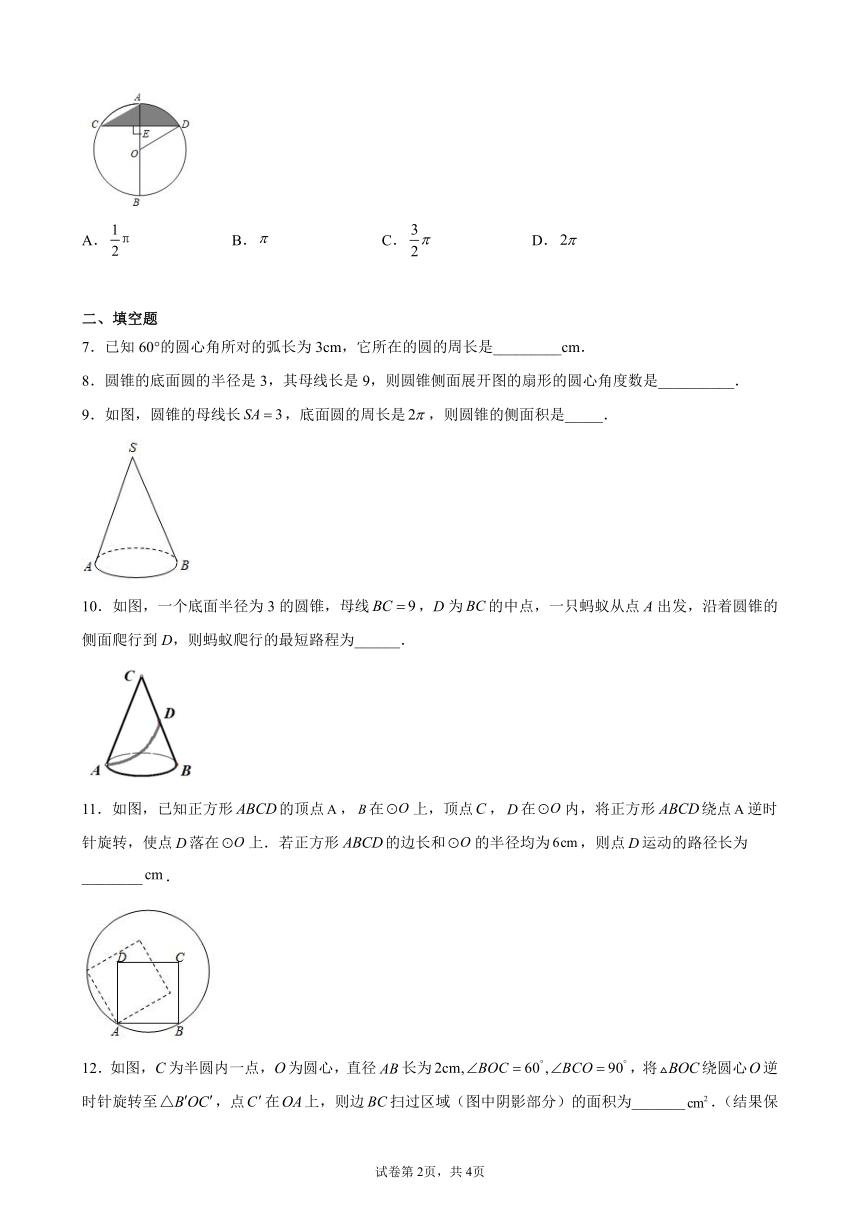
6.如图,是的直径,弦,垂足为, ,,则等于( )
A. B. C. D.
二、填空题
7.已知60°的圆心角所对的弧长为3cm,它所在的圆的周长是_________cm.
8.圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是__________.
9.如图,圆锥的母线长,底面圆的周长是,则圆锥的侧面积是_____.
10.如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
11.如图,已知正方形的顶点,在上,顶点,在内,将正方形绕点逆时针旋转,使点落在上.若正方形的边长和的半径均为,则点运动的路径长为________.
12.如图,为半圆内一点,为圆心,直径长为,将绕圆心逆时针旋转至,点在上,则边扫过区域(图中阴影部分)的面积为_______.(结果保留).
三、解答题
13.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:),电镀时,如果每平方米用锌,电镀100个这样的锚标浮筒,需要用多少锌?
14.有一圆锥形塔尖,它的侧面积是14.13 m2,底面圆的半径等于1.5 m,求这个塔尖的高(精确到0.1 m).
15.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
16.如图,有一个马戏帐篷,它的底面是圆形,其半径为,从A到B有一笔直的栅栏,其长为.观众在阴影区域里看马戏,如果每平方米可以坐3名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
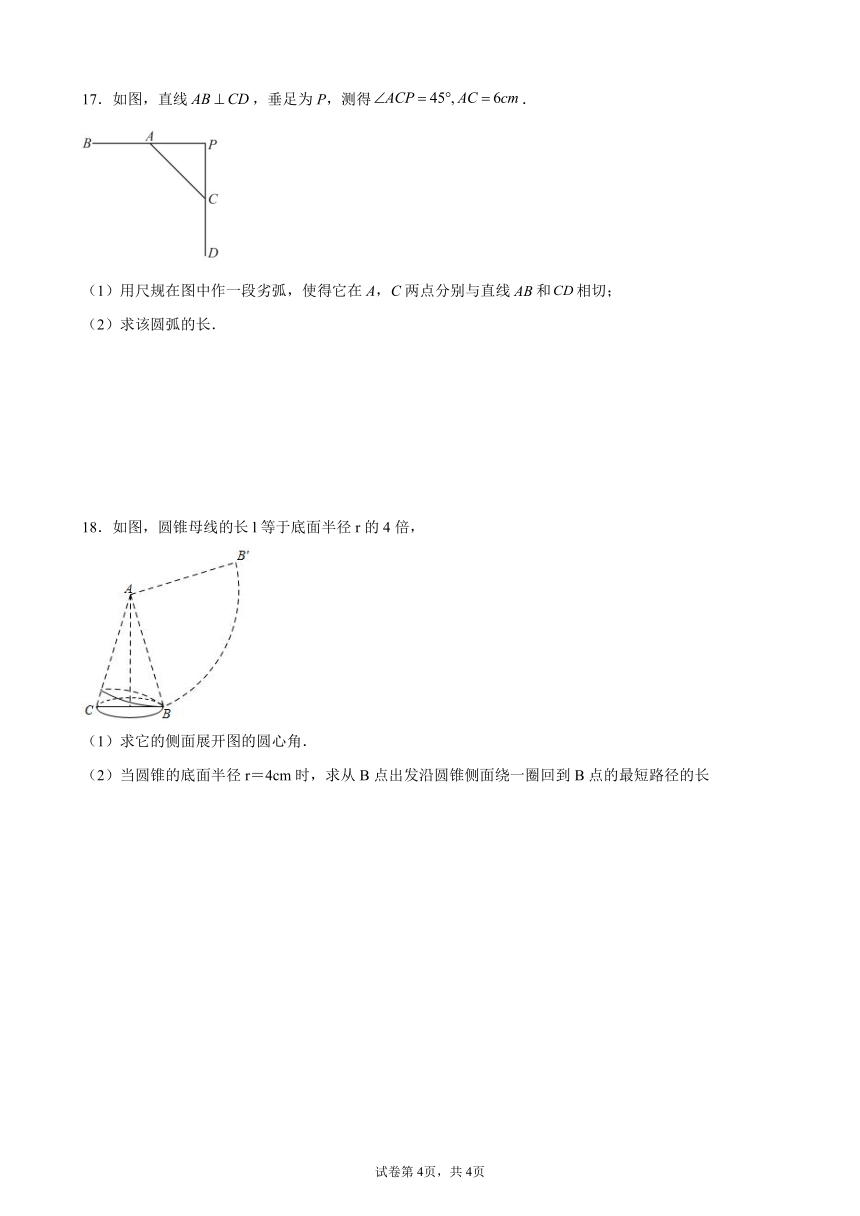
17.如图,直线,垂足为P,测得.
(1)用尺规在图中作一段劣弧,使得它在A,C两点分别与直线和相切;
(2)求该圆弧的长.
18.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
参考答案
1.A
【解析】解:连接,,
∵,
∴是等边三角形.
∴,
∴,
∴的长为.
故选A.
2.C
【解析】解:由题意得,2π=,
解得:n=180.
即这条弧所对的圆心角的度数是180°.
故选C.
3.C
【解析】解:由题意得扇形的面积是.
故选C.
4.A
【解析】依题意可求出弧长AC的长度为=
∵弧长AC的长度等于圆锥的底面半径,设圆锥的底面半径为r
∴
解得r=1
故选A.
5.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
6.D
【解析】解:,,
,
在中,,
则,
在中,,
则,
,
.
故选:D.
7.18
【解析】.
故答案为:18.
8.120
【解析】解:根据题意得,
故答案为:120.
9.
【解析】解:根据题意得该圆锥的侧面积.
故答案为:.
10.
【解析】画出圆锥侧面展开图如下:
如图,连接AB、AD,
设圆锥侧面展开图的圆心角的度数为,
因为圆锥侧面展开图是一个扇形,扇形的弧长等于底面圆的周长,扇形的半径等于母线长,
所以,
解得,
则,
又,
是等边三角形,
点D是BC的中点,
,,
在中,,
由两点之间线段最短可知,蚂蚁爬行的最短路程为,
故答案为:.
11.
【解析】如图,设圆心为,连接,,,,,
∵,,
∴,
∴是等边三角形,
∴,同理,是等边三角形,,
∴旋转角,
∵,
∴点运动的路径长为:.
故答案是.
12.
【解析】解:,△是绕圆心逆时针旋转得到的,
,△,
,,
,
,
,,
,
,
,
阴影部分面积;
故答案为:.
13.11.44πkg
【解析】解:由图形可知圆锥的底面圆的半径为400mm=0.4m,
圆锥的高为300mm=0.3m,
则圆锥的母线长为:=0.5m.
∴圆锥的侧面积=π×0.4×0.5=0.2π(m2),
∵圆柱的高为800mm=0.8m.
圆柱的侧面积=2π×0.4×0.8=0.64π(m2),
∴浮筒的表面积==2S圆锥侧面积+S圆柱侧面积,=1.04π(m2),
∵每平方米用锌0.11kg,
∴一个浮筒需用锌:1.04π×0.11kg,
∴100个这样的锚标浮筒需用锌:100×1.04π×0.11=11.44π(kg).
答:100个这样的锚标浮筒需用锌11.44πkg.
14.约2.6 m.
【解析】如图:
则圆锥的底面周长为:
圆锥的侧面积=
则这个塔尖的高
答:这个塔尖的高约2.6 m.
15.
【解析】解:连接OD.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),弧BC=弧BD
故S△OCE=S△ODE,∠COB=∠DOB,
∴S阴=S扇形OBD ,
又∵∠CDB=30°,
∴∠COB=∠DOB=60°(圆周角定理),
∴∠OCB=30°
∴OC=,
解得:,
故S扇形OBD= =,
即阴影部分的面积为.
16.约421人.
【解析】解:过O作OD⊥AB,D为垂足,
∵AB=30m.
∴AD=BD=15m,
∴OD==5
∵sin∠AOD===0.75,
∴∠AOD≈49°,
∴∠AOB=98°,
∴S阴影部分=S扇形OAB-S△OAB=-×30×5≈145.7m2,
∴145.7×3≈437(人).
答:大约有437位观众在看马戏.
17.(1)答案见解析;(2).
【解析】解:(1)分别从点A,C处作垂线,两垂线相交于点O,以点O为圆心,OA为半径作圆,弧AC就是所求的劣弧;
(2)由题意及作图过程可得:∠AOC=90°,
∵∠ACP=45°,AC=6cm,
∴OA==cm,
∴弧AC==cm.
18.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
试卷第4页,共4页
试卷第1页,共4页
3.9弧长及扇形的面积-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正方形的边长,分别以点,为圆心,长为半径画弧,两弧交于点,则的长是( )
A. B. C. D.
2.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
3.在圆心角为的扇形中,半径,则扇形的面积是( )
A. B. C. D.
4.如图,在边长为4的正方形内部裁得一个扇形,若将该扇形围成一个圆锥,则此圆锥的底面半径为( )
A.1 B. C. D.2
5.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
6.如图,是的直径,弦,垂足为, ,,则等于( )
A. B. C. D.
二、填空题
7.已知60°的圆心角所对的弧长为3cm,它所在的圆的周长是_________cm.
8.圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是__________.
9.如图,圆锥的母线长,底面圆的周长是,则圆锥的侧面积是_____.
10.如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
11.如图,已知正方形的顶点,在上,顶点,在内,将正方形绕点逆时针旋转,使点落在上.若正方形的边长和的半径均为,则点运动的路径长为________.
12.如图,为半圆内一点,为圆心,直径长为,将绕圆心逆时针旋转至,点在上,则边扫过区域(图中阴影部分)的面积为_______.(结果保留).
三、解答题
13.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:),电镀时,如果每平方米用锌,电镀100个这样的锚标浮筒,需要用多少锌?
14.有一圆锥形塔尖,它的侧面积是14.13 m2,底面圆的半径等于1.5 m,求这个塔尖的高(精确到0.1 m).
15.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
16.如图,有一个马戏帐篷,它的底面是圆形,其半径为,从A到B有一笔直的栅栏,其长为.观众在阴影区域里看马戏,如果每平方米可以坐3名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
17.如图,直线,垂足为P,测得.
(1)用尺规在图中作一段劣弧,使得它在A,C两点分别与直线和相切;
(2)求该圆弧的长.
18.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
参考答案
1.A
【解析】解:连接,,
∵,
∴是等边三角形.
∴,
∴,
∴的长为.
故选A.
2.C
【解析】解:由题意得,2π=,
解得:n=180.
即这条弧所对的圆心角的度数是180°.
故选C.
3.C
【解析】解:由题意得扇形的面积是.
故选C.
4.A
【解析】依题意可求出弧长AC的长度为=
∵弧长AC的长度等于圆锥的底面半径,设圆锥的底面半径为r
∴
解得r=1
故选A.
5.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
6.D
【解析】解:,,
,
在中,,
则,
在中,,
则,
,
.
故选:D.
7.18
【解析】.
故答案为:18.
8.120
【解析】解:根据题意得,
故答案为:120.
9.
【解析】解:根据题意得该圆锥的侧面积.
故答案为:.
10.
【解析】画出圆锥侧面展开图如下:
如图,连接AB、AD,
设圆锥侧面展开图的圆心角的度数为,
因为圆锥侧面展开图是一个扇形,扇形的弧长等于底面圆的周长,扇形的半径等于母线长,
所以,
解得,
则,
又,
是等边三角形,
点D是BC的中点,
,,
在中,,
由两点之间线段最短可知,蚂蚁爬行的最短路程为,
故答案为:.
11.
【解析】如图,设圆心为,连接,,,,,
∵,,
∴,
∴是等边三角形,
∴,同理,是等边三角形,,
∴旋转角,
∵,
∴点运动的路径长为:.
故答案是.
12.
【解析】解:,△是绕圆心逆时针旋转得到的,
,△,
,,
,
,
,,
,
,
,
阴影部分面积;
故答案为:.
13.11.44πkg
【解析】解:由图形可知圆锥的底面圆的半径为400mm=0.4m,
圆锥的高为300mm=0.3m,
则圆锥的母线长为:=0.5m.
∴圆锥的侧面积=π×0.4×0.5=0.2π(m2),
∵圆柱的高为800mm=0.8m.
圆柱的侧面积=2π×0.4×0.8=0.64π(m2),
∴浮筒的表面积==2S圆锥侧面积+S圆柱侧面积,=1.04π(m2),
∵每平方米用锌0.11kg,
∴一个浮筒需用锌:1.04π×0.11kg,
∴100个这样的锚标浮筒需用锌:100×1.04π×0.11=11.44π(kg).
答:100个这样的锚标浮筒需用锌11.44πkg.
14.约2.6 m.
【解析】如图:
则圆锥的底面周长为:
圆锥的侧面积=
则这个塔尖的高
答:这个塔尖的高约2.6 m.
15.
【解析】解:连接OD.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),弧BC=弧BD
故S△OCE=S△ODE,∠COB=∠DOB,
∴S阴=S扇形OBD ,
又∵∠CDB=30°,
∴∠COB=∠DOB=60°(圆周角定理),
∴∠OCB=30°
∴OC=,
解得:,
故S扇形OBD= =,
即阴影部分的面积为.
16.约421人.
【解析】解:过O作OD⊥AB,D为垂足,
∵AB=30m.
∴AD=BD=15m,
∴OD==5
∵sin∠AOD===0.75,
∴∠AOD≈49°,
∴∠AOB=98°,
∴S阴影部分=S扇形OAB-S△OAB=-×30×5≈145.7m2,
∴145.7×3≈437(人).
答:大约有437位观众在看马戏.
17.(1)答案见解析;(2).
【解析】解:(1)分别从点A,C处作垂线,两垂线相交于点O,以点O为圆心,OA为半径作圆,弧AC就是所求的劣弧;
(2)由题意及作图过程可得:∠AOC=90°,
∵∠ACP=45°,AC=6cm,
∴OA==cm,
∴弧AC==cm.
18.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
试卷第4页,共4页
试卷第1页,共4页
