2021—2022学年人教版数学八年级下册16.2.2二次根式的除法 课件(共25张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册16.2.2二次根式的除法 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 12:03:14 | ||
图片预览






文档简介
(共25张PPT)
16.2.2
二次根式的除法
第十六章 二次根式
人教版八年级下册
学习目标
1.经历探索二次根式除法法则的推导过程;
2.掌握二次根式除法法则,能灵活正用和逆用二次根式的除法运算;
3.理解最简二次根式的概念并能用最简二次根式的概念进行二次根式的化简.
重、难点:
二次根式除法法则的灵活用运和最简二次根式的掌握.
新课引入
这两个式子该如何计算呢?
我们知道,两个二次根式可以进行乘法运算,那
么,两个二次根式能否进行除法运算呢?
.
探究新知
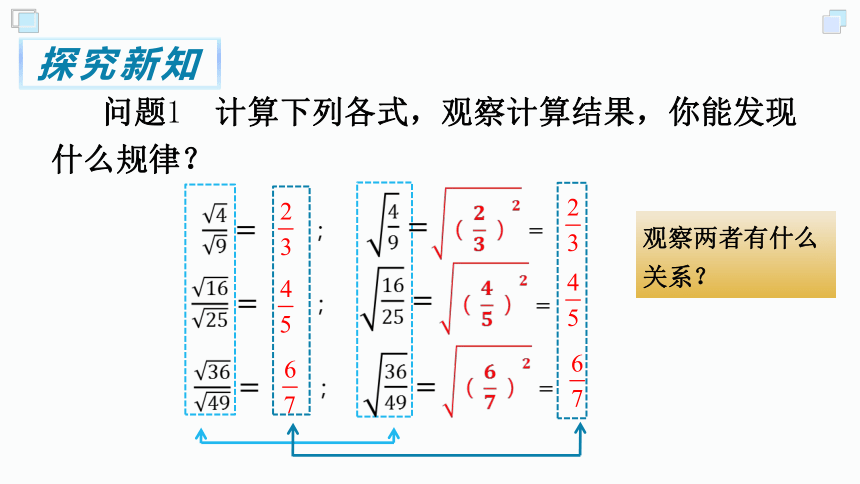
问题1 计算下列各式,观察计算结果,你能发现
什么规律?
观察两者有什么关系?
探究新知
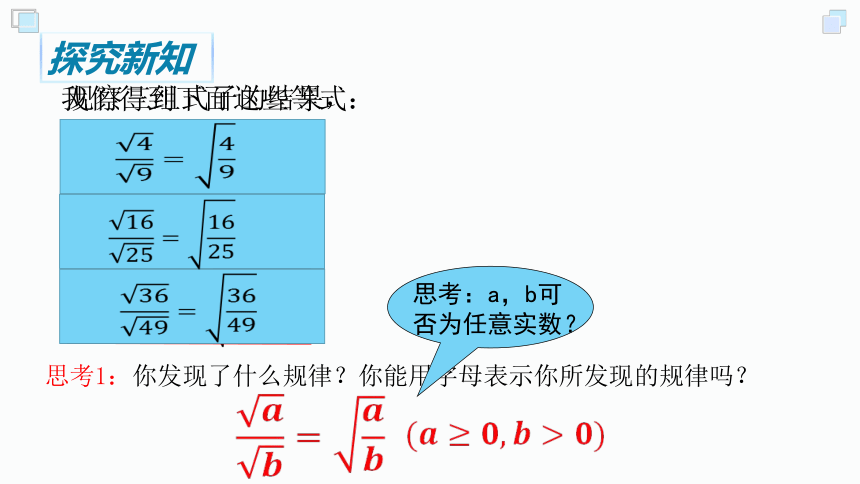
思考1:你发现了什么规律?你能用字母表示你所发现的规律吗?
思考:a,b可否为任意实数?
我们得到下面这些等式:
观察三组式子的结果,
求证:
证明:根据积的乘方法则,有
又∵
∴ .
证一证
一般地,对于二次根式的除法是
语言表述:
商的算术平方根等于各个被开方数商的算术平方根.
二次根式的除法法则:
探究新知
即二次根式相乘,________不变,________相除.
根指数
被开方数
例1 计算:
例题精讲
解:
(1) (2)
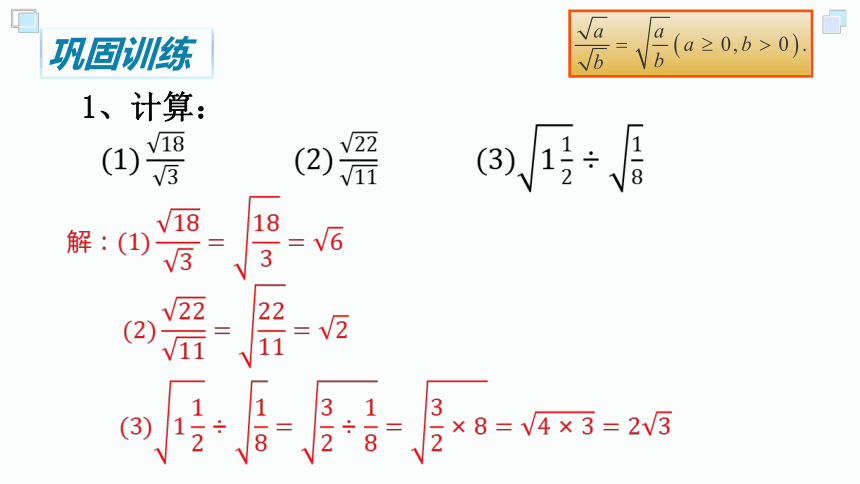
巩固训练
1、计算:
解:
能力提高
计算:
当二次根式根号外的因数不为1时,可先将根号前的系数与系数对应相除,根号内的被开方数与被开方数对应相除,再把得出的的结果相乘,即乘单项式的法则计算,即
.
归纳
探究新知
问题2 能否将二次根式 化简?
把 反过来,就得到
(a≥0,b>0)
利用它可以进行二次根式的化简.
解:
例2 化简:
例题精讲
解:
例3 计算:
例题精讲
解:
这一步是为了去掉分母中的根号。
例3 计算:
例题精讲
;
;
.
解:
例4 化简:
解:
能力提升
例4 化简:
解:
能力提升
例4 化简:
能力提升
二次根式 化简的两种形式
(1)分数形式:当被开方数为分数形式时,利用 化简。
(2)小数或带分数形式:当被开方数为小数或者带分数形式时,先化为分数或者假分数形式后再利用(1)进行化简。
归纳
练一练
化简:
观察例1,例2,例3中各小题的最后结果,比如
探究新知
问题3 观察上面各小题计算的最后结果并思考:
(1)你觉得这些结果能否再化简,它们已经是最简二次根式了吗?
是最简二次根式
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条 件就可以说它是最简了?
这三个二次根式的被开方数都不含分母和开得尽方的因数或因式
二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
归纳总结
我们把满足上述两个条件的二次根式,叫做最简二次根式.
最简二次根式简记为:(1)分母无根号,根号下无分母;
(2)不能再开方。
练一练
辨别下列二次根式是否是最简二次根式.
(1) (2) (3) (4)
×
×
×
×
×
√
√
√
例4
例题精讲
设长方形的面积为S,相邻两边长分别为a,b.已知S=2 ,b= ,求a.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
课堂小结
1.二次根式的除法法则是什么
2.最简二次根式有什么特征?
当堂检测
1、计算:
2、把下列二次根式化为最简二次根式:
教材10页习题16.2第2、4、10题.
课后作业
16.2.2
二次根式的除法
第十六章 二次根式
人教版八年级下册
学习目标
1.经历探索二次根式除法法则的推导过程;
2.掌握二次根式除法法则,能灵活正用和逆用二次根式的除法运算;
3.理解最简二次根式的概念并能用最简二次根式的概念进行二次根式的化简.
重、难点:
二次根式除法法则的灵活用运和最简二次根式的掌握.
新课引入
这两个式子该如何计算呢?
我们知道,两个二次根式可以进行乘法运算,那
么,两个二次根式能否进行除法运算呢?
.
探究新知
问题1 计算下列各式,观察计算结果,你能发现
什么规律?
观察两者有什么关系?
探究新知
思考1:你发现了什么规律?你能用字母表示你所发现的规律吗?
思考:a,b可否为任意实数?
我们得到下面这些等式:
观察三组式子的结果,
求证:
证明:根据积的乘方法则,有
又∵
∴ .
证一证
一般地,对于二次根式的除法是
语言表述:
商的算术平方根等于各个被开方数商的算术平方根.
二次根式的除法法则:
探究新知
即二次根式相乘,________不变,________相除.
根指数
被开方数
例1 计算:
例题精讲
解:
(1) (2)
巩固训练
1、计算:
解:
能力提高
计算:
当二次根式根号外的因数不为1时,可先将根号前的系数与系数对应相除,根号内的被开方数与被开方数对应相除,再把得出的的结果相乘,即乘单项式的法则计算,即
.
归纳
探究新知
问题2 能否将二次根式 化简?
把 反过来,就得到
(a≥0,b>0)
利用它可以进行二次根式的化简.
解:
例2 化简:
例题精讲
解:
例3 计算:
例题精讲
解:
这一步是为了去掉分母中的根号。
例3 计算:
例题精讲
;
;
.
解:
例4 化简:
解:
能力提升
例4 化简:
解:
能力提升
例4 化简:
能力提升
二次根式 化简的两种形式
(1)分数形式:当被开方数为分数形式时,利用 化简。
(2)小数或带分数形式:当被开方数为小数或者带分数形式时,先化为分数或者假分数形式后再利用(1)进行化简。
归纳
练一练
化简:
观察例1,例2,例3中各小题的最后结果,比如
探究新知
问题3 观察上面各小题计算的最后结果并思考:
(1)你觉得这些结果能否再化简,它们已经是最简二次根式了吗?
是最简二次根式
(2)这些结果有什么共同特点,你认为一个二次根式满足什么条 件就可以说它是最简了?
这三个二次根式的被开方数都不含分母和开得尽方的因数或因式
二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
归纳总结
我们把满足上述两个条件的二次根式,叫做最简二次根式.
最简二次根式简记为:(1)分母无根号,根号下无分母;
(2)不能再开方。
练一练
辨别下列二次根式是否是最简二次根式.
(1) (2) (3) (4)
×
×
×
×
×
√
√
√
例4
例题精讲
设长方形的面积为S,相邻两边长分别为a,b.已知S=2 ,b= ,求a.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
课堂小结
1.二次根式的除法法则是什么
2.最简二次根式有什么特征?
当堂检测
1、计算:
2、把下列二次根式化为最简二次根式:
教材10页习题16.2第2、4、10题.
课后作业
