2021-2022学年人教版数学八年级下册17.1勾股定理教学课件(17张ppt)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.1勾股定理教学课件(17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 12:31:52 | ||
图片预览




文档简介
(共17张PPT)
勾股定理
探索:
看到这个方砖地图案,你能发现什么?
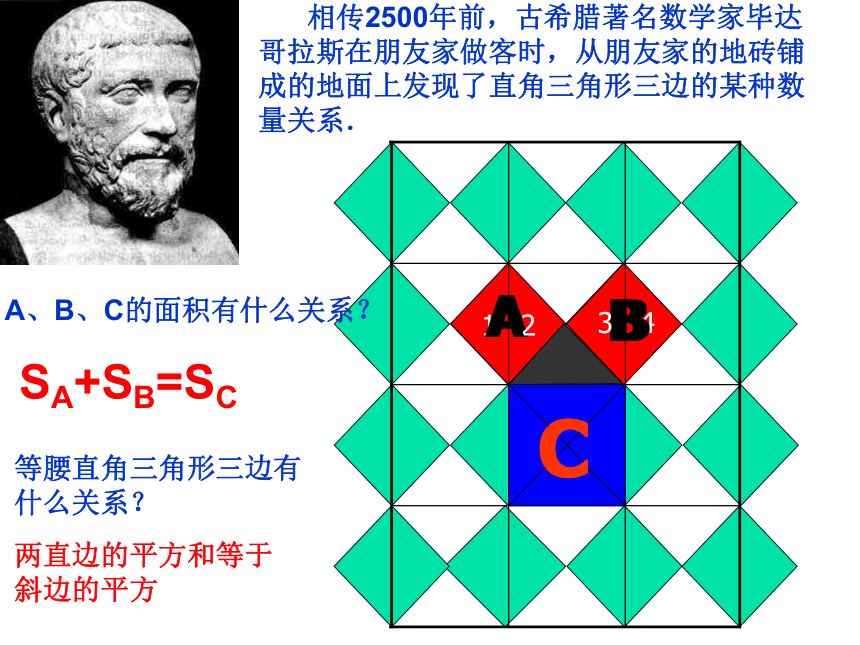
相传2500年前,古希腊著名数学家毕达哥拉斯在朋友家做客时,从朋友家的地砖铺成的地面上发现了直角三角形三边的某种数量关系.
A
B
C
A、B、C的面积有什么关系?
等腰直角三角形三边有
什么关系?
SA+SB=SC
两直边的平方和等于
斜边的平方
1
2
3
4
A
B
C
探究与猜想
是不是一般的直角三角形的三边都满足这种关系呢
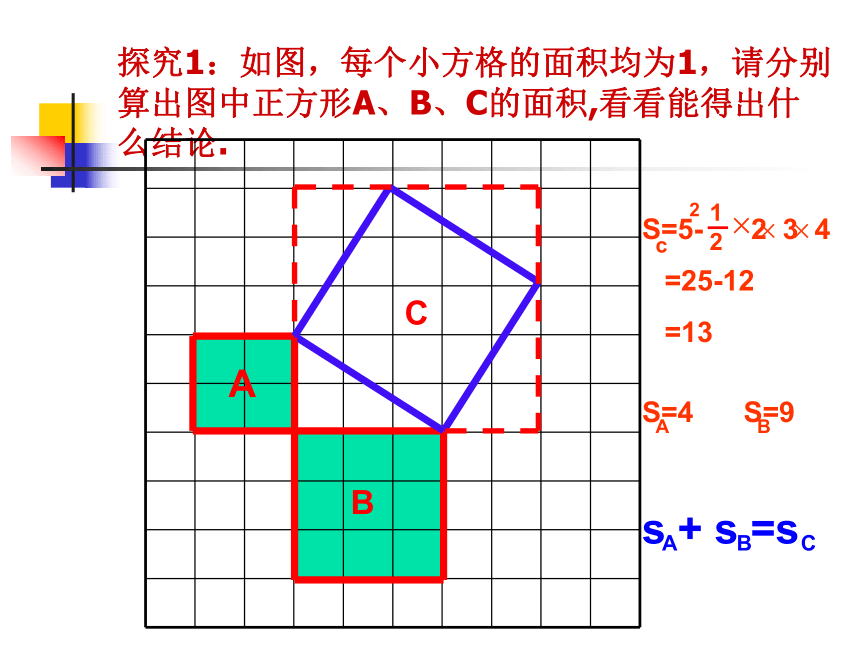
探究1:如图,每个小方格的面积均为1,请分别算出图中正方形A、B、C的面积,看看能得出什么结论.
A
B
C
1
2
=25-12
=13
2
×
×
×
c
S=4
A
S=9
B
s + s =s
A
B
C
S=5- 2 3 4
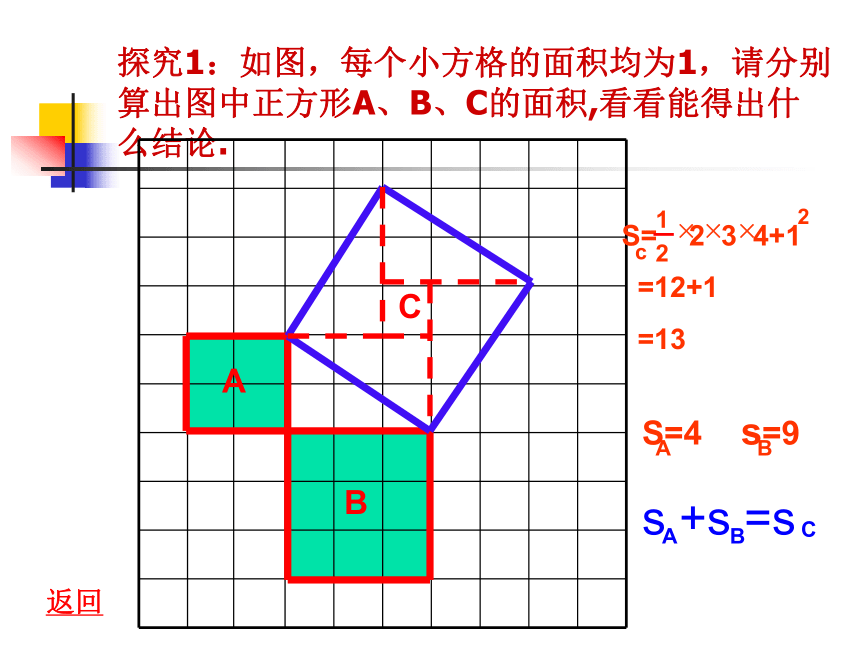
探究1:如图,每个小方格的面积均为1,请分别算出图中正方形A、B、C的面积,看看能得出什么结论.
A
B
C
S= 2 3 4+1
=12+1
=13
×
×
×
2
1
2
c
S=4 s=9
s +s =s
A
B
A
B
C
返回
由此,我们可猜想出:
怎么证明呢?
活动:
1.任意剪4个全等的直角三角形,直角边分别用a 、b表示,斜边用c表示;
2.用这4个全等的直角三角形拼一拼,摆一摆,看能否得到一个含有以斜边c为边长的正方形;
3.通过拼图和计算,你能验证直角三角形三边之间的关系吗?
拼图:
图1
图2
b
a
b-a
(a+b)= ab 4+c
a +2ab+b =2ab+c
a +b =c
ab 4+(b-a)=c
2ab+b -2ab+a =c
a +b =c
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
×
×
1
2
1
2
经过证明被确认正确的命题叫做定理.
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
巩固新知
625
576
144
169
X=81+144
2
Y=169-144
Z=625-576
2
2
X=15
Y=5
Z=7
勾股定理的运用一
已知直角三角形的任意两条边长,求第三条边长.
a2=c2-b2
b2=c2-a2
c2=a2+b2
在直角三角形ABC中,∠C=900,∠A、∠B、∠C所对的边分别为a、b、c
(1) 已知a=1,b=2,求c
(2) 已知a=10,c=15,求b
小试牛刀
A
C
B
b
a
c
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。
回顾反思
布置作业:
1.课堂作业:课本p78第1、2、3题,p79页第11题.
2.课外作业:收集有关勾股定理的证明方法.
本节课结束
同学们,再见!
勾股定理
探索:
看到这个方砖地图案,你能发现什么?
相传2500年前,古希腊著名数学家毕达哥拉斯在朋友家做客时,从朋友家的地砖铺成的地面上发现了直角三角形三边的某种数量关系.
A
B
C
A、B、C的面积有什么关系?
等腰直角三角形三边有
什么关系?
SA+SB=SC
两直边的平方和等于
斜边的平方
1
2
3
4
A
B
C
探究与猜想
是不是一般的直角三角形的三边都满足这种关系呢
探究1:如图,每个小方格的面积均为1,请分别算出图中正方形A、B、C的面积,看看能得出什么结论.
A
B
C
1
2
=25-12
=13
2
×
×
×
c
S=4
A
S=9
B
s + s =s
A
B
C
S=5- 2 3 4
探究1:如图,每个小方格的面积均为1,请分别算出图中正方形A、B、C的面积,看看能得出什么结论.
A
B
C
S= 2 3 4+1
=12+1
=13
×
×
×
2
1
2
c
S=4 s=9
s +s =s
A
B
A
B
C
返回
由此,我们可猜想出:
怎么证明呢?
活动:
1.任意剪4个全等的直角三角形,直角边分别用a 、b表示,斜边用c表示;
2.用这4个全等的直角三角形拼一拼,摆一摆,看能否得到一个含有以斜边c为边长的正方形;
3.通过拼图和计算,你能验证直角三角形三边之间的关系吗?
拼图:
图1
图2
b
a
b-a
(a+b)= ab 4+c
a +2ab+b =2ab+c
a +b =c
ab 4+(b-a)=c
2ab+b -2ab+a =c
a +b =c
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
×
×
1
2
1
2
经过证明被确认正确的命题叫做定理.
勾 股 世 界
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理”
求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
巩固新知
625
576
144
169
X=81+144
2
Y=169-144
Z=625-576
2
2
X=15
Y=5
Z=7
勾股定理的运用一
已知直角三角形的任意两条边长,求第三条边长.
a2=c2-b2
b2=c2-a2
c2=a2+b2
在直角三角形ABC中,∠C=900,∠A、∠B、∠C所对的边分别为a、b、c
(1) 已知a=1,b=2,求c
(2) 已知a=10,c=15,求b
小试牛刀
A
C
B
b
a
c
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。
回顾反思
布置作业:
1.课堂作业:课本p78第1、2、3题,p79页第11题.
2.课外作业:收集有关勾股定理的证明方法.
本节课结束
同学们,再见!
