【单元复习课件】第五章 相交线与平行线 课件(共6张PPT)
文档属性
| 名称 | 【单元复习课件】第五章 相交线与平行线 课件(共6张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 00:00:00 | ||
图片预览


文档简介
(共6张PPT)
相交线与平行线章节复习
(人教版)
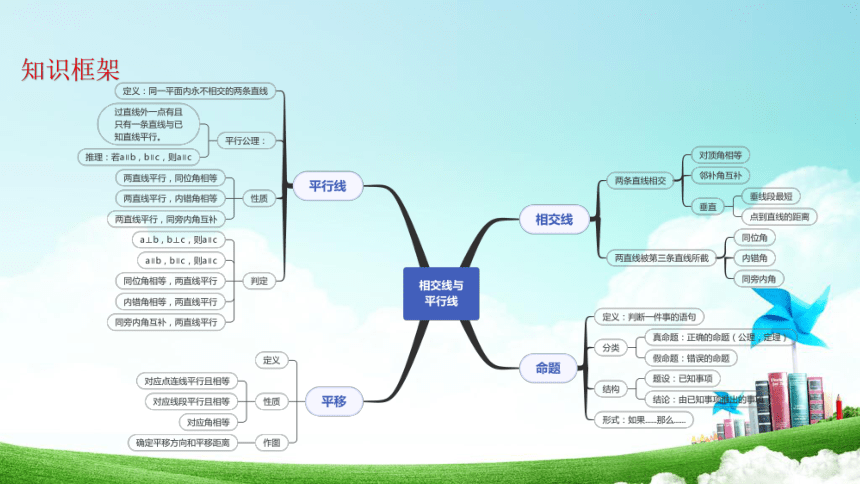
知识框架
知识清单详解
知识点一:相交线
解析:直接利用角平分线定义结合平角的定义再根据对顶角或邻补角得出答案.
1.邻补角与对顶角
邻补角互补。即:
∠1+∠3=180°,∠1+∠2=180°
∠3+∠4=180°,∠2+∠4=180°
对顶角相等。即:
∠1=∠4,∠3=∠2
注意:邻补角一定互补,互补的两个角不一定是邻补角。对顶角一定相等,相等的两个角不一定是对顶角。
2. 垂线
(1)如图即垂直
(2)性质:①垂线段最短
②垂线段的长度表示距离。
③过一点有且只有一条直线与已知直线垂直。
3. 两条直线被第三条直线所截:同位角、内错角以及同旁内角。
例题:
类型一:邻补角与对顶角性质的应用
如图,直线AB与直线CD交于点O.OE、OC分别是∠AOC与∠BOE的角平分线,则
∠AOD为( )
A.45° B.50°
C.55° D.60°
解:∵OE、OC分别是∠AOC与∠BOE的角平分线,
∴∠AOE=∠EOC,∠EOC=∠BOC,
∴∠AOE=∠EOC=∠BOC,
∵∠AOE+∠EOC+∠BOC=180°,
∴∠AOE=∠EOC=∠BOC=60°,
∴∠AOD=60°.
故选:D.
D
解析:利用垂线段最短得到AD≥AC,然后对各选项进行判断
解:∵AC⊥BC,AC=4,
∴AD≥AC,即AD≥4.
观察选项,只有选项A符合题意.
故选:A.
A
例题:
类型二:垂直及其性质
如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5
C.5 D.5.5
解析:根据同位角、内错角、同旁内角的意义结合图形进行判断即可.
解:如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;
∠1与∠4不是内错角,因此选项B符合题意;
∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;
∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;
故选:B.
B
例题:
类型三:同位角、内错角以及同旁内角的判断
如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角
B.∠1与∠4是内错角
C.∠5与∠6是内错角
D.∠3与∠5是同位角
知识点二:平行线
1.定义及其性质:
(1)定义:如图:a与b是平行线。a∥b。
(2)性质:①两直线平行,同位角相等。a∥b,则∠1=∠5;
②两直线平行,内错角相等。a∥b,则∠3=∠4;
③两直线平行,同旁内角互补。a∥b,则∠3+∠5=180°。
2.平行公理及其推论:
(1)公理:过直线外一点有且只有一条直线与已知直线平行。
(2)推论:a∥c,b∥c,则a∥b。
3.平行线的判定:
(1)a⊥c,b⊥c,则a∥b;
(2)a∥c,b∥c,则a∥b;
(3)同位角相等,两直线平行。即∠1=∠5,则a∥b;
(4)内错角相等,两直线平行。即∠3=∠4,则a∥b;
(5)同旁内角互补,两直线平行。即∠3+∠5=180°,则a∥b。
解析:根据平行线的性质和三角板的角度解答即可.
解:∵DE∥AF,
∴∠CED=∠EAF=46°,
∵∠BAC=90°-30°=60°,
∴∠BAF=∠BAC-∠EAF=60°-46°=14°,
故选:C.
C
例题:
类型一:平行线及其性质
将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48° B.16°
C.14° D.32°
解析:直接利用平行公理以及其推论分析得出答案.
解:①由定义可知错误;②在同一平面内,两条直线的位置关系只有两种:相交和平行,正确;
③由平行的定义可知错误;④由平行公理可知正确;
⑤由平行公理的推论可知错误,
故选:B.
例题:
类型二:平行公理及其推论
下列语句:
①不相交的两条直线叫平行线;②在同一平面内,两条直线的位置关系只有两种:相交和平行;③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;④如果两条直线都和第三条直线平行,那么这两条直线平行;⑤过一点有且只有一条直线与已知直线平行。
正确的个数是( )
A.1 B.2 C.3 D.4
B
解析:根据内错角相等两直线平行、同旁内角互补两直线平行逐一判断即可.
解:A.由∠1=∠2可判断AD∥BC,不符合题意;
B.∠BAD=∠BCD不能判定图中直线平行,不符合题意;
C.由∠BAD+∠ADC=180°可判定AB∥DC,符合题意;
D.由∠3=∠4可判定AD∥BC,不符合题意;
故选:C.
C
例题:
类型三:平行线的判定
如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2
B.∠BAD=∠BCD
C.∠BAD+∠ADC=180°
D.∠3=∠4
解析:求出∠3+∠FHD=180°,根据平行线的判定得出FG∥BD,根据平行线的性质得出∠1=∠ABD,根据角平分线的定义得出∠ABD=∠2即可.
例题:
类型四:平行线的性质与判定
如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2.(请通过填空完善下列推理过程)
解:∵∠3+∠4=180°(已知)
∠FHD=∠4( )
∴∠3+ =180°(等量代换).
∴FG∥BD( ).
∴∠1= ( ).
∵BD平分∠ABC,
∴∠ABD= ( ).
∴∠1=∠2( ).
对顶角相等
∠FHD
同旁内角互补,两直线平行
∠ABD
两直线平行,同位角相等
∠2
角平分线的定义
等量代换
知识点三:命题、定理以及证明
1.命题:
(1)定义:判断一件事情的话语
(2)分类:真命题和假命题
(3)构成:题设+结论构成
(4)形式:如果......那么......
2.定理:通过推理证明得到的真命题叫做定理。
3.证明:推理证实真命题的过程叫做证明。
解析:写出各命题,再判断命题的真假即可.
D
例题:
类型一:命题、定理以及证明
如图所示,已知BE平分∠ABC,CE平分∠BCD.另有三个条件:①AB∥CD;②∠1+∠2=90°;
③∠ABE+∠DCE=∠BEC.以①、②、③其中一个为条件,另一个为结论组成命题,在组成的所有命题中,是真命题的个数有( )
A.3个 B.4个
C.5个 D.6个
解:命题1,若①,则②;
∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵BE平分∠ABC,CE平分∠BCD,
∴∠1= ∠ABC,∠2= ∠BCD,
∴∠1+∠2= (∠ABC+∠BCD)=90°,故此命题是真命题;
解:命题2,若①,则③;
∵AB∥CD,
∴∠1+∠ABE+∠2+∠DCE=180°.
∵∠1+∠2+∠BEC=180°,
∴∠ABE+∠DCE=∠BEC,故此命题是真命题;
解:命题3,若②,则①;
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∵∠1+∠2=90°,
∴∠ABC+∠BCD=2(∠1+∠2)=180°,
∴AB∥CD,故此命题是真命题;
解:命题4,若②,则③;
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∵∠1+∠2=90°,
∴∠ABC+∠BCD=2(∠1+∠2)=180°∴∠ABE+∠DCE=90°.
∵∠1+∠2+∠BEC=180°,
∴∠ABE+∠DCE=∠BEC,故此命题是真命题;
解:命题5,若③,则②;
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABE= ∠ABC,∠DCE= ∠BCD,
∵∠ABE+∠DCE=∠BEC,∠1+∠2+∠BEC=180°,
∴∠1+∠2=90°,故此命题是真命题;
解:命题6,若③,则①.
∵∠ABE+∠DCE=∠BEC,∠BEC+∠1+∠2=180°,
∴∠ABE+∠DCE+∠1+∠2=180°,即∠ABC+∠BCD=180°,
∴AB∥CD,故此命题是真命题.
故选:D.
知识点四:平移
1. 平移
(1)定义:把一个图形沿一定方向移动一定距离得到一个新图形,这种移动就叫做平移。
(2)平移要素:平移方向和平移距离。
(3)对应元素:对应点;
对应线段;
对应角。
(4)性质:①对应线段平行且相等。
②对应角相等。
③对应点的连线平行且相等。
注意:有一种特殊情况是在同一直线上。
(5)平移作图步骤:
找出关键点+确定平移方向+确定平移距离。把平移后的关键点连接即可。
解析:根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移进行解答即可.
解:①电梯的升降运动,是平移;
②飞机在地面沿直线滑行,是平移;
③风车的转动,不是平移;
④汽车轮胎的转动,不是平移,
故选:C.
C
例题:
类型一:生活中的平移现象——理解定义
以下现象:
①电梯的升降运动;
②飞机在地面沿直线滑行;
③风车的转动;
④汽车轮胎的转动.其中属于平移的是( )
A.②③ B.②④ C.①② D.①④
解析:根据平移的性质,结合图形可直接求解.
解:观察图形可知,对应点连接的线段是AD、BE和CF.
∵△ABC沿BC方向平移3cm得到△DEF,
∴BE=CF=3cm,
∴∠F=∠ACB=180°-∠A-∠B=40°,
故答案为:3cm,40°.
例题:
类型二:平移的性质
将△ABC沿BC方向平移3cm得到△DEF,则CF= ;若∠A=80°,∠B=60°,则∠F= .
3cm
40°
相交线与平行线章节复习
(人教版)
知识框架
知识清单详解
知识点一:相交线
解析:直接利用角平分线定义结合平角的定义再根据对顶角或邻补角得出答案.
1.邻补角与对顶角
邻补角互补。即:
∠1+∠3=180°,∠1+∠2=180°
∠3+∠4=180°,∠2+∠4=180°
对顶角相等。即:
∠1=∠4,∠3=∠2
注意:邻补角一定互补,互补的两个角不一定是邻补角。对顶角一定相等,相等的两个角不一定是对顶角。
2. 垂线
(1)如图即垂直
(2)性质:①垂线段最短
②垂线段的长度表示距离。
③过一点有且只有一条直线与已知直线垂直。
3. 两条直线被第三条直线所截:同位角、内错角以及同旁内角。
例题:
类型一:邻补角与对顶角性质的应用
如图,直线AB与直线CD交于点O.OE、OC分别是∠AOC与∠BOE的角平分线,则
∠AOD为( )
A.45° B.50°
C.55° D.60°
解:∵OE、OC分别是∠AOC与∠BOE的角平分线,
∴∠AOE=∠EOC,∠EOC=∠BOC,
∴∠AOE=∠EOC=∠BOC,
∵∠AOE+∠EOC+∠BOC=180°,
∴∠AOE=∠EOC=∠BOC=60°,
∴∠AOD=60°.
故选:D.
D
解析:利用垂线段最短得到AD≥AC,然后对各选项进行判断
解:∵AC⊥BC,AC=4,
∴AD≥AC,即AD≥4.
观察选项,只有选项A符合题意.
故选:A.
A
例题:
类型二:垂直及其性质
如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5
C.5 D.5.5
解析:根据同位角、内错角、同旁内角的意义结合图形进行判断即可.
解:如图,∠1与∠2是直线a与直线b被直线c所截的同旁内角,因此选项A不符合题意;
∠1与∠4不是内错角,因此选项B符合题意;
∠5与∠6是直线c与直线d被直线b所截的内错角,因此选项C不符合题意;
∠3与∠5是直线c与直线d被直线b所截的同位角,因此选项D不符合题意;
故选:B.
B
例题:
类型三:同位角、内错角以及同旁内角的判断
如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角
B.∠1与∠4是内错角
C.∠5与∠6是内错角
D.∠3与∠5是同位角
知识点二:平行线
1.定义及其性质:
(1)定义:如图:a与b是平行线。a∥b。
(2)性质:①两直线平行,同位角相等。a∥b,则∠1=∠5;
②两直线平行,内错角相等。a∥b,则∠3=∠4;
③两直线平行,同旁内角互补。a∥b,则∠3+∠5=180°。
2.平行公理及其推论:
(1)公理:过直线外一点有且只有一条直线与已知直线平行。
(2)推论:a∥c,b∥c,则a∥b。
3.平行线的判定:
(1)a⊥c,b⊥c,则a∥b;
(2)a∥c,b∥c,则a∥b;
(3)同位角相等,两直线平行。即∠1=∠5,则a∥b;
(4)内错角相等,两直线平行。即∠3=∠4,则a∥b;
(5)同旁内角互补,两直线平行。即∠3+∠5=180°,则a∥b。
解析:根据平行线的性质和三角板的角度解答即可.
解:∵DE∥AF,
∴∠CED=∠EAF=46°,
∵∠BAC=90°-30°=60°,
∴∠BAF=∠BAC-∠EAF=60°-46°=14°,
故选:C.
C
例题:
类型一:平行线及其性质
将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48° B.16°
C.14° D.32°
解析:直接利用平行公理以及其推论分析得出答案.
解:①由定义可知错误;②在同一平面内,两条直线的位置关系只有两种:相交和平行,正确;
③由平行的定义可知错误;④由平行公理可知正确;
⑤由平行公理的推论可知错误,
故选:B.
例题:
类型二:平行公理及其推论
下列语句:
①不相交的两条直线叫平行线;②在同一平面内,两条直线的位置关系只有两种:相交和平行;③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;④如果两条直线都和第三条直线平行,那么这两条直线平行;⑤过一点有且只有一条直线与已知直线平行。
正确的个数是( )
A.1 B.2 C.3 D.4
B
解析:根据内错角相等两直线平行、同旁内角互补两直线平行逐一判断即可.
解:A.由∠1=∠2可判断AD∥BC,不符合题意;
B.∠BAD=∠BCD不能判定图中直线平行,不符合题意;
C.由∠BAD+∠ADC=180°可判定AB∥DC,符合题意;
D.由∠3=∠4可判定AD∥BC,不符合题意;
故选:C.
C
例题:
类型三:平行线的判定
如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2
B.∠BAD=∠BCD
C.∠BAD+∠ADC=180°
D.∠3=∠4
解析:求出∠3+∠FHD=180°,根据平行线的判定得出FG∥BD,根据平行线的性质得出∠1=∠ABD,根据角平分线的定义得出∠ABD=∠2即可.
例题:
类型四:平行线的性质与判定
如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2.(请通过填空完善下列推理过程)
解:∵∠3+∠4=180°(已知)
∠FHD=∠4( )
∴∠3+ =180°(等量代换).
∴FG∥BD( ).
∴∠1= ( ).
∵BD平分∠ABC,
∴∠ABD= ( ).
∴∠1=∠2( ).
对顶角相等
∠FHD
同旁内角互补,两直线平行
∠ABD
两直线平行,同位角相等
∠2
角平分线的定义
等量代换
知识点三:命题、定理以及证明
1.命题:
(1)定义:判断一件事情的话语
(2)分类:真命题和假命题
(3)构成:题设+结论构成
(4)形式:如果......那么......
2.定理:通过推理证明得到的真命题叫做定理。
3.证明:推理证实真命题的过程叫做证明。
解析:写出各命题,再判断命题的真假即可.
D
例题:
类型一:命题、定理以及证明
如图所示,已知BE平分∠ABC,CE平分∠BCD.另有三个条件:①AB∥CD;②∠1+∠2=90°;
③∠ABE+∠DCE=∠BEC.以①、②、③其中一个为条件,另一个为结论组成命题,在组成的所有命题中,是真命题的个数有( )
A.3个 B.4个
C.5个 D.6个
解:命题1,若①,则②;
∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵BE平分∠ABC,CE平分∠BCD,
∴∠1= ∠ABC,∠2= ∠BCD,
∴∠1+∠2= (∠ABC+∠BCD)=90°,故此命题是真命题;
解:命题2,若①,则③;
∵AB∥CD,
∴∠1+∠ABE+∠2+∠DCE=180°.
∵∠1+∠2+∠BEC=180°,
∴∠ABE+∠DCE=∠BEC,故此命题是真命题;
解:命题3,若②,则①;
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∵∠1+∠2=90°,
∴∠ABC+∠BCD=2(∠1+∠2)=180°,
∴AB∥CD,故此命题是真命题;
解:命题4,若②,则③;
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABC=2∠1,∠BCD=2∠2.
∵∠1+∠2=90°,
∴∠ABC+∠BCD=2(∠1+∠2)=180°∴∠ABE+∠DCE=90°.
∵∠1+∠2+∠BEC=180°,
∴∠ABE+∠DCE=∠BEC,故此命题是真命题;
解:命题5,若③,则②;
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABE= ∠ABC,∠DCE= ∠BCD,
∵∠ABE+∠DCE=∠BEC,∠1+∠2+∠BEC=180°,
∴∠1+∠2=90°,故此命题是真命题;
解:命题6,若③,则①.
∵∠ABE+∠DCE=∠BEC,∠BEC+∠1+∠2=180°,
∴∠ABE+∠DCE+∠1+∠2=180°,即∠ABC+∠BCD=180°,
∴AB∥CD,故此命题是真命题.
故选:D.
知识点四:平移
1. 平移
(1)定义:把一个图形沿一定方向移动一定距离得到一个新图形,这种移动就叫做平移。
(2)平移要素:平移方向和平移距离。
(3)对应元素:对应点;
对应线段;
对应角。
(4)性质:①对应线段平行且相等。
②对应角相等。
③对应点的连线平行且相等。
注意:有一种特殊情况是在同一直线上。
(5)平移作图步骤:
找出关键点+确定平移方向+确定平移距离。把平移后的关键点连接即可。
解析:根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移进行解答即可.
解:①电梯的升降运动,是平移;
②飞机在地面沿直线滑行,是平移;
③风车的转动,不是平移;
④汽车轮胎的转动,不是平移,
故选:C.
C
例题:
类型一:生活中的平移现象——理解定义
以下现象:
①电梯的升降运动;
②飞机在地面沿直线滑行;
③风车的转动;
④汽车轮胎的转动.其中属于平移的是( )
A.②③ B.②④ C.①② D.①④
解析:根据平移的性质,结合图形可直接求解.
解:观察图形可知,对应点连接的线段是AD、BE和CF.
∵△ABC沿BC方向平移3cm得到△DEF,
∴BE=CF=3cm,
∴∠F=∠ACB=180°-∠A-∠B=40°,
故答案为:3cm,40°.
例题:
类型二:平移的性质
将△ABC沿BC方向平移3cm得到△DEF,则CF= ;若∠A=80°,∠B=60°,则∠F= .
3cm
40°
