华东师大版2021-2022年初中数学七年级下册7.4实践与探索同步课堂练习(Word版含答案)
文档属性
| 名称 | 华东师大版2021-2022年初中数学七年级下册7.4实践与探索同步课堂练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 327.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 08:49:13 | ||
图片预览



文档简介
2021-2022年初中数学七年级下册同步(华东师大版)
7.4实践与探索-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲是乙现在的年龄时,乙8岁,乙是甲现在的年龄时,甲26岁,那么( )
A.甲20岁,乙14岁 B.甲22岁,乙16岁
C.乙比甲大18岁 D.乙比甲大34岁
2.如图,8块相同的小长方形地砖拼成一个长方形,其中每一个小长方形的面积为( )
A. B. C. D.
3.开学后书店向学校推销两类素质教育书,如果原价买这两种书共需880元,书店推销时第一种书打了八折,第二种书打了七五折,结果两种书共少要了200元,则原来每种书需钱数为( ).
A.400元,480元 B.480元,400元 C.360元,300元 D.300元,360元
4.甲乙丙三人做一项工作,三人每天的工作效率分别为a、b、c,若甲乙一天工作量和是丙2天的工作量,乙丙一天的工作量和是甲5天的工作量,下列结论正确的是( )
A.甲的工作效率最高 B.丙的工作效率最高 C.c=3a D.b:c=3:2
5.一个两位数,个位与十位的数字之和是11;如果原数加45,等于此两位数的数字位置对调后得到的新的两位数,那么原数是多少?若设原数十位数字为x,个位数字为y,则列出的方程组应为( )
A. B.
C. D.以上均不对
6.一盒糖果均分给若干个小朋友,如果每个小朋友分9粒则多出10粒,如果每人分10粒,则缺4粒,则小朋友的人数是( )
A.15人 B.14人 C.13人 D.以上都不对
二、填空题
7.体育馆的环形跑道长400米,甲、乙分别以一定的速度练习长跑和骑自行车.如果同向而行80秒乙追上甲一次;如果反向而行,他们每隔30秒相遇一次;求甲、乙的速度分别是多少?如果设甲的速度是米秒,乙的速度是米秒,所列方程组是________.
8.现有x本练习本分给y个学生,每人分4本,余12本,每人分5本则少10本,那么练习本有_________本,学生有_________人.
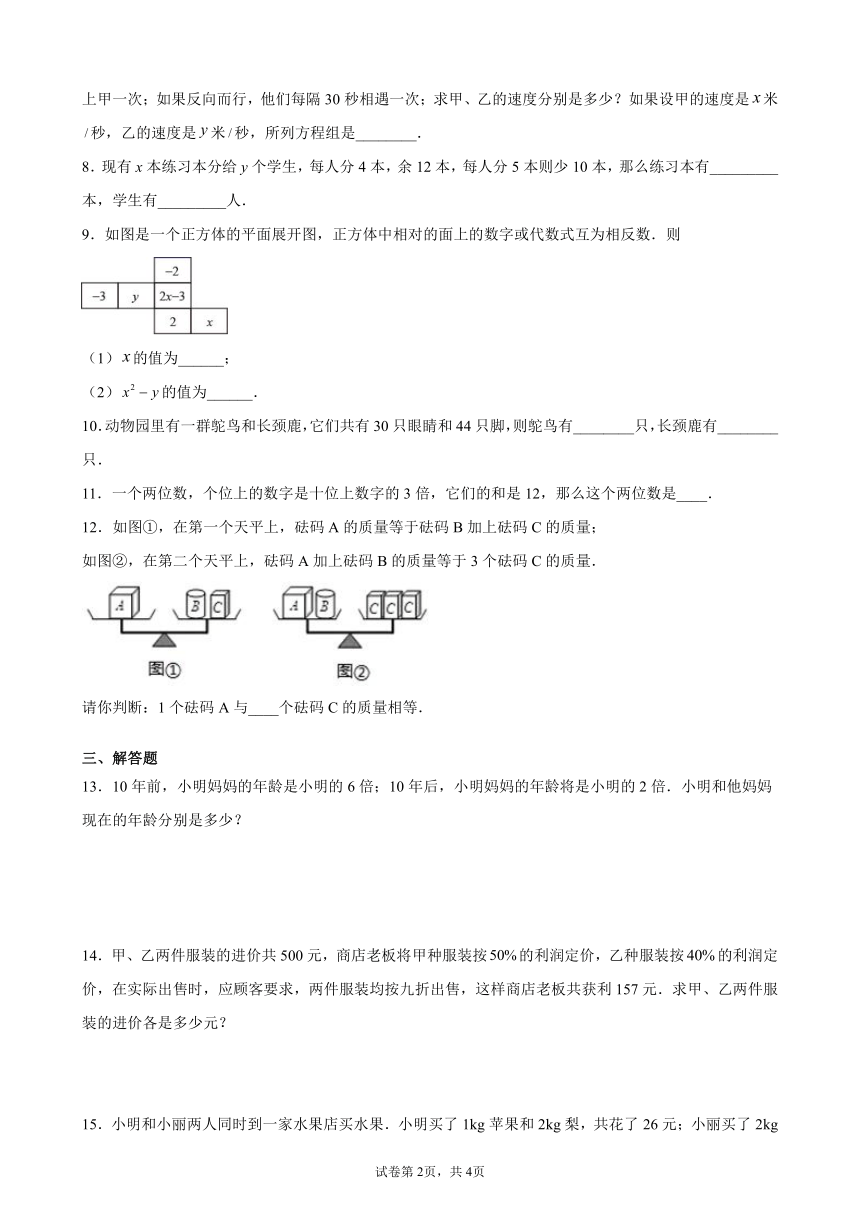
9.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则
(1)的值为______;
(2)的值为______.
10.动物园里有一群鸵鸟和长颈鹿,它们共有30只眼睛和44只脚,则鸵鸟有________只,长颈鹿有________只.
11.一个两位数,个位上的数字是十位上数字的3倍,它们的和是12,那么这个两位数是____.
12.如图①,在第一个天平上,砝码A的质量等于砝码B加上砝码C的质量;
如图②,在第二个天平上,砝码A加上砝码B的质量等于3个砝码C的质量.
请你判断:1个砝码A与____个砝码C的质量相等.
三、解答题
13.10年前,小明妈妈的年龄是小明的6倍;10年后,小明妈妈的年龄将是小明的2倍.小明和他妈妈现在的年龄分别是多少?
14.甲、乙两件服装的进价共500元,商店老板将甲种服装按的利润定价,乙种服装按的利润定价,在实际出售时,应顾客要求,两件服装均按九折出售,这样商店老板共获利157元.求甲、乙两件服装的进价各是多少元?
15.小明和小丽两人同时到一家水果店买水果.小明买了1kg苹果和2kg梨,共花了26元;小丽买了2kg苹果和1kg梨,共花了28元.苹果和梨的价格各为多少?
根据题意,小明列出方程组:
而小丽列出的是:
交流后,他们发现两个方程组不同,于是展开了争论,都说自己是正确的,而对方是错误的.他们列的方程组正确吗?你认为他们产生分歧的原因是什么?
16.如图,把8块相同的小长方形地砖拼成一块大长方形地砖.
(1)每块小长方形地砖的长和宽分别是多少?(要求列方程组进行解答)
(2)小明想用一块面积为的正方形地毯,沿着边的方向裁剪出一块新的长方形地毯,用来盖住这块大长方形地砖你帮小明算一算,他能剪出符合要求的地毯吗?
17.某商场计划拨款万元从厂家购进台电视机,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台元,乙种每台元,丙种每台元.
若商场同时购进其中两种不同型号的电视机台,用去万元,请你研究一下商场的进货方案;
若商场销售一台甲、乙、丙电视机分别可获利元,元,元,在以上的方案中,为使获利最多,商场应选择哪种进货方案?
18.一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
参考答案
1.A
【解析】设甲现在的年龄为x岁,乙现在的年龄为y岁.
依题意得,解.
故选A
2.A
【解析】解:设一个小长方形的长为xcm,宽为ycm,
则可列方程组组:,
解得:,
则一个小正方形的面积=45cm×15cm=675cm2.
故选:A.
3.A
【解析】解:设原来第一种书需钱x元,第二种书需钱y元,根据题意得:
,
解得:
所以原来每种书需钱数为400元,480元.
故选:A.
4.D
【解析】解:由题意可得:
①-②,得
解得:,故C错误;
将代入①,得
解得:
∴b>c>a
∴乙的工作效率最高,故A、B错误;
b:c=3a:2a=3:2,故D正确.
故选D.
5.C
【解析】解:设原数十位数字为x,个位数字为y,
根据题意,得;
故选:C.
6.B
【解析】设有位小朋友,粒糖果,
根据题意得:,
解得:,
∴小朋友的人数是14人,
故选:B.
7.
【解析】解:根据题意,得
.
故答案为:.
8.100 22
【解析】∵学生人数为y个,练习本有x本
依题意得:,
解得:,
故答案为:,.
9.3 12
【解析】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,“-3”与“2x 3”是相对面,“y”与“x”是相对面,
∵相对的面上的数字或代数式互为相反数,
∴2x 3+(-3)=0,x+y=0,
解得x=3,y=-3,
故答案是:3;
(2)当x=3,y=-3时,=,
故答案是:12.
10.8 7
【解析】设有x只鸵鸟,y只长颈鹿,根据题意得方程组解这个方程组得
11.39
【解析】设个位上数字是,十位上数字为,
依题意得
解得
所以这个两位数为39.
故答案为39.
12.2
【解析】由图一可列方程:A=B+C (1),可变化为B=A-C(2).
由图二可列方程:A+B=C+C+C(3).
将(2)式代入(3)式,可消去B,得到 A+A-C=C+C+C,
化简得到A=2C
13.小明和他妈妈现在的年龄分别是15岁和40岁
【解析】设小明和他妈妈现在的年龄分别是x岁和y岁,根据题意,
得
解得
答:小明和他妈妈现在的年龄分别是15岁和40岁.
14.甲服装的进价是300元,乙服装的进价是200元.
【解析】解:设甲服装的成本是x元,乙服装的成本是y元,
根据题意可得:,
解得:.
答:甲服装的进价是300元,乙服装的进价是200元.
15.他们列的方程组都正确,见解析
【解析】解:两个人所列的方程都是正确的,理由如下:
由题意得:小明设每千克苹果和梨的价格分别为x元、y元,而小丽设每千克梨和苹果的价格分别为x元、y元,
因此他们所列方程组中,同一个x的意义不同,当然所列方程组也就不相同了.
16.(1)每块小长方形地砖的长为15cm,宽为5cm.;(2)小明不能剪出符合要求的地毯.
【解析】(1)设每块小长方形地砖的长为xcm,宽为ycm.
依题意,得,解得.
答:每块小长方形地砖的长为15cm,宽为5cm.
(2)正方形桌布的面积为,
桌布的边长为.
,
小明不能剪出符合要求的地毯.
17.有种方案.方案一:甲种台,乙种台;方案二:甲种台,丙种台;购买甲种电视机台,丙种电视机台获利最多.所以应选择方案二.
【解析】(1)①设购进甲台,乙台,
;
∴;
∴购进甲台,乙台.
②设购进甲台,丙台
;
∴;
购进甲台,丙台.
③设购进乙台,丙台
;
∴(舍)
所以选择有种方案.方案一:甲种台,乙种台;
方案二:甲种台,丙种台;
(2)利润应为:方案一:元,
方案二:元,
∵元元,∴ 方案二获利多,
购买甲种电视机台,丙种电视机台获利最多.所以应选择方案二.
18.(1)甲组工作一天商店应付300元,乙组工作一天商店应付140元;(2)单独请乙组所需费用最少;(3)商店请甲乙两组同时装修,才更有利,理由见解析.
【解析】(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,
根据题意得:,
解得:.
答:甲组工作一天商店应付300元,乙组工作一天商店应付140元.
(2)单独请甲组所需费用为:300×12=3600(元),
单独请乙组所需费用为:140×24=3360(元).
∵3600>3360,
∴单独请乙组所需费用最少.
(3)商店请甲乙两组同时装修,才更有利.理由如下:
单独请甲组完成,损失钱数为:200×12+3600=6000(元),
单独请乙组完成,损失钱数为:200×24+3360=8160(元),
请甲乙两组同时完成,损失钱数为:200×8+3520=5120(元).
∵8160>6000>5120,
∴商店请甲乙两组同时装修,才更有利.
试卷第4页,共4页
试卷第3页,共4页
7.4实践与探索-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲是乙现在的年龄时,乙8岁,乙是甲现在的年龄时,甲26岁,那么( )
A.甲20岁,乙14岁 B.甲22岁,乙16岁
C.乙比甲大18岁 D.乙比甲大34岁
2.如图,8块相同的小长方形地砖拼成一个长方形,其中每一个小长方形的面积为( )
A. B. C. D.
3.开学后书店向学校推销两类素质教育书,如果原价买这两种书共需880元,书店推销时第一种书打了八折,第二种书打了七五折,结果两种书共少要了200元,则原来每种书需钱数为( ).
A.400元,480元 B.480元,400元 C.360元,300元 D.300元,360元
4.甲乙丙三人做一项工作,三人每天的工作效率分别为a、b、c,若甲乙一天工作量和是丙2天的工作量,乙丙一天的工作量和是甲5天的工作量,下列结论正确的是( )
A.甲的工作效率最高 B.丙的工作效率最高 C.c=3a D.b:c=3:2
5.一个两位数,个位与十位的数字之和是11;如果原数加45,等于此两位数的数字位置对调后得到的新的两位数,那么原数是多少?若设原数十位数字为x,个位数字为y,则列出的方程组应为( )
A. B.
C. D.以上均不对
6.一盒糖果均分给若干个小朋友,如果每个小朋友分9粒则多出10粒,如果每人分10粒,则缺4粒,则小朋友的人数是( )
A.15人 B.14人 C.13人 D.以上都不对
二、填空题
7.体育馆的环形跑道长400米,甲、乙分别以一定的速度练习长跑和骑自行车.如果同向而行80秒乙追上甲一次;如果反向而行,他们每隔30秒相遇一次;求甲、乙的速度分别是多少?如果设甲的速度是米秒,乙的速度是米秒,所列方程组是________.
8.现有x本练习本分给y个学生,每人分4本,余12本,每人分5本则少10本,那么练习本有_________本,学生有_________人.
9.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则
(1)的值为______;
(2)的值为______.
10.动物园里有一群鸵鸟和长颈鹿,它们共有30只眼睛和44只脚,则鸵鸟有________只,长颈鹿有________只.
11.一个两位数,个位上的数字是十位上数字的3倍,它们的和是12,那么这个两位数是____.
12.如图①,在第一个天平上,砝码A的质量等于砝码B加上砝码C的质量;
如图②,在第二个天平上,砝码A加上砝码B的质量等于3个砝码C的质量.
请你判断:1个砝码A与____个砝码C的质量相等.
三、解答题
13.10年前,小明妈妈的年龄是小明的6倍;10年后,小明妈妈的年龄将是小明的2倍.小明和他妈妈现在的年龄分别是多少?
14.甲、乙两件服装的进价共500元,商店老板将甲种服装按的利润定价,乙种服装按的利润定价,在实际出售时,应顾客要求,两件服装均按九折出售,这样商店老板共获利157元.求甲、乙两件服装的进价各是多少元?
15.小明和小丽两人同时到一家水果店买水果.小明买了1kg苹果和2kg梨,共花了26元;小丽买了2kg苹果和1kg梨,共花了28元.苹果和梨的价格各为多少?
根据题意,小明列出方程组:
而小丽列出的是:
交流后,他们发现两个方程组不同,于是展开了争论,都说自己是正确的,而对方是错误的.他们列的方程组正确吗?你认为他们产生分歧的原因是什么?
16.如图,把8块相同的小长方形地砖拼成一块大长方形地砖.
(1)每块小长方形地砖的长和宽分别是多少?(要求列方程组进行解答)
(2)小明想用一块面积为的正方形地毯,沿着边的方向裁剪出一块新的长方形地毯,用来盖住这块大长方形地砖你帮小明算一算,他能剪出符合要求的地毯吗?
17.某商场计划拨款万元从厂家购进台电视机,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台元,乙种每台元,丙种每台元.
若商场同时购进其中两种不同型号的电视机台,用去万元,请你研究一下商场的进货方案;
若商场销售一台甲、乙、丙电视机分别可获利元,元,元,在以上的方案中,为使获利最多,商场应选择哪种进货方案?
18.一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
参考答案
1.A
【解析】设甲现在的年龄为x岁,乙现在的年龄为y岁.
依题意得,解.
故选A
2.A
【解析】解:设一个小长方形的长为xcm,宽为ycm,
则可列方程组组:,
解得:,
则一个小正方形的面积=45cm×15cm=675cm2.
故选:A.
3.A
【解析】解:设原来第一种书需钱x元,第二种书需钱y元,根据题意得:
,
解得:
所以原来每种书需钱数为400元,480元.
故选:A.
4.D
【解析】解:由题意可得:
①-②,得
解得:,故C错误;
将代入①,得
解得:
∴b>c>a
∴乙的工作效率最高,故A、B错误;
b:c=3a:2a=3:2,故D正确.
故选D.
5.C
【解析】解:设原数十位数字为x,个位数字为y,
根据题意,得;
故选:C.
6.B
【解析】设有位小朋友,粒糖果,
根据题意得:,
解得:,
∴小朋友的人数是14人,
故选:B.
7.
【解析】解:根据题意,得
.
故答案为:.
8.100 22
【解析】∵学生人数为y个,练习本有x本
依题意得:,
解得:,
故答案为:,.
9.3 12
【解析】解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形,“-3”与“2x 3”是相对面,“y”与“x”是相对面,
∵相对的面上的数字或代数式互为相反数,
∴2x 3+(-3)=0,x+y=0,
解得x=3,y=-3,
故答案是:3;
(2)当x=3,y=-3时,=,
故答案是:12.
10.8 7
【解析】设有x只鸵鸟,y只长颈鹿,根据题意得方程组解这个方程组得
11.39
【解析】设个位上数字是,十位上数字为,
依题意得
解得
所以这个两位数为39.
故答案为39.
12.2
【解析】由图一可列方程:A=B+C (1),可变化为B=A-C(2).
由图二可列方程:A+B=C+C+C(3).
将(2)式代入(3)式,可消去B,得到 A+A-C=C+C+C,
化简得到A=2C
13.小明和他妈妈现在的年龄分别是15岁和40岁
【解析】设小明和他妈妈现在的年龄分别是x岁和y岁,根据题意,
得
解得
答:小明和他妈妈现在的年龄分别是15岁和40岁.
14.甲服装的进价是300元,乙服装的进价是200元.
【解析】解:设甲服装的成本是x元,乙服装的成本是y元,
根据题意可得:,
解得:.
答:甲服装的进价是300元,乙服装的进价是200元.
15.他们列的方程组都正确,见解析
【解析】解:两个人所列的方程都是正确的,理由如下:
由题意得:小明设每千克苹果和梨的价格分别为x元、y元,而小丽设每千克梨和苹果的价格分别为x元、y元,
因此他们所列方程组中,同一个x的意义不同,当然所列方程组也就不相同了.
16.(1)每块小长方形地砖的长为15cm,宽为5cm.;(2)小明不能剪出符合要求的地毯.
【解析】(1)设每块小长方形地砖的长为xcm,宽为ycm.
依题意,得,解得.
答:每块小长方形地砖的长为15cm,宽为5cm.
(2)正方形桌布的面积为,
桌布的边长为.
,
小明不能剪出符合要求的地毯.
17.有种方案.方案一:甲种台,乙种台;方案二:甲种台,丙种台;购买甲种电视机台,丙种电视机台获利最多.所以应选择方案二.
【解析】(1)①设购进甲台,乙台,
;
∴;
∴购进甲台,乙台.
②设购进甲台,丙台
;
∴;
购进甲台,丙台.
③设购进乙台,丙台
;
∴(舍)
所以选择有种方案.方案一:甲种台,乙种台;
方案二:甲种台,丙种台;
(2)利润应为:方案一:元,
方案二:元,
∵元元,∴ 方案二获利多,
购买甲种电视机台,丙种电视机台获利最多.所以应选择方案二.
18.(1)甲组工作一天商店应付300元,乙组工作一天商店应付140元;(2)单独请乙组所需费用最少;(3)商店请甲乙两组同时装修,才更有利,理由见解析.
【解析】(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元,
根据题意得:,
解得:.
答:甲组工作一天商店应付300元,乙组工作一天商店应付140元.
(2)单独请甲组所需费用为:300×12=3600(元),
单独请乙组所需费用为:140×24=3360(元).
∵3600>3360,
∴单独请乙组所需费用最少.
(3)商店请甲乙两组同时装修,才更有利.理由如下:
单独请甲组完成,损失钱数为:200×12+3600=6000(元),
单独请乙组完成,损失钱数为:200×24+3360=8160(元),
请甲乙两组同时完成,损失钱数为:200×8+3520=5120(元).
∵8160>6000>5120,
∴商店请甲乙两组同时装修,才更有利.
试卷第4页,共4页
试卷第3页,共4页
