5.2平面直角坐标系

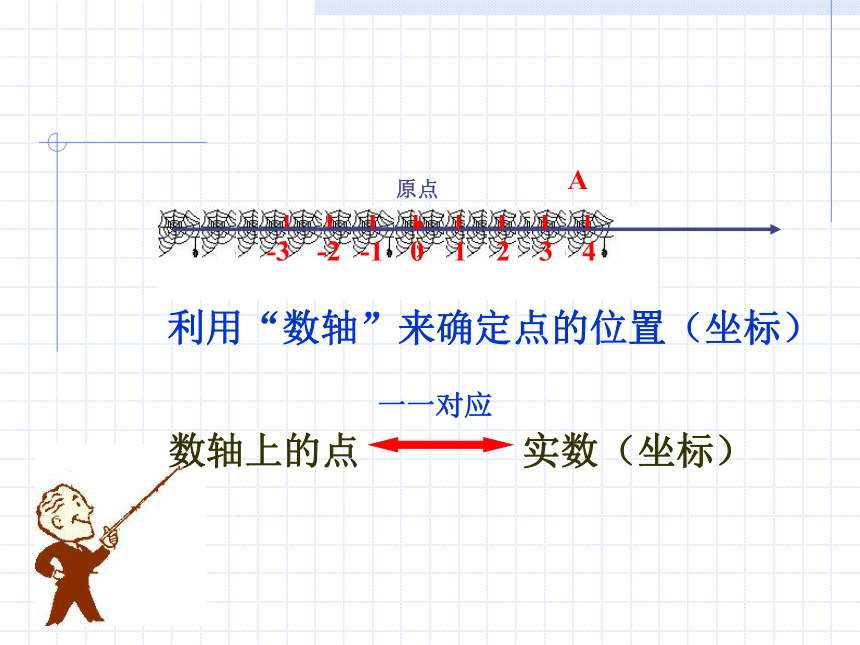
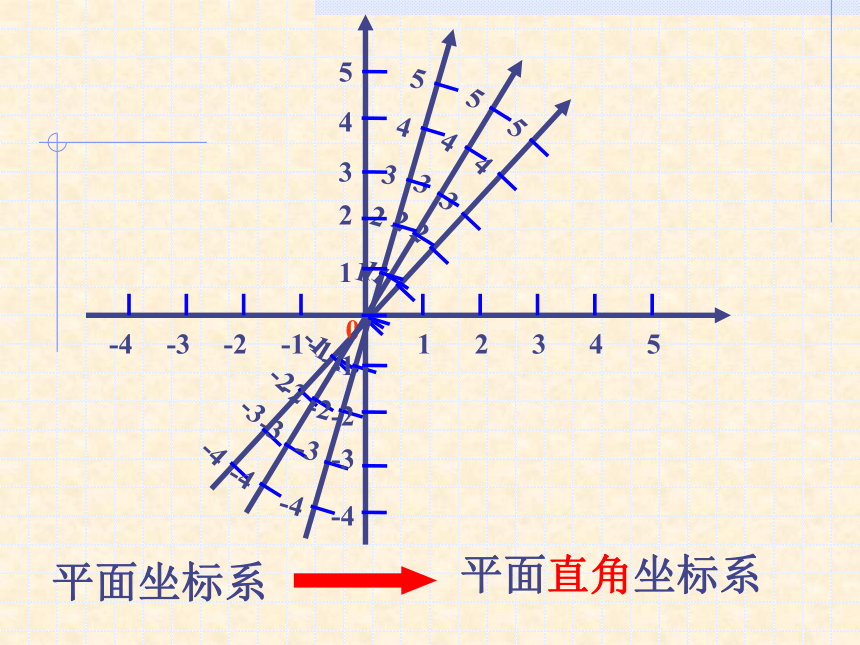
课件56张PPT。5.2 平面直角坐标系 利用“数轴”来确定点的位置（坐标）A数轴上的点 实数（坐标）一一对应平面坐标系平面直角坐标系学习目标：
（1）理解平面直角坐标系的有关概念，能正确画出
直角坐标系。
（2）能在平面直角坐标系中，根据坐标找出点，由
点求出坐标。
( 3 ) 了解平面内的点与有序实数对之间的一一对应
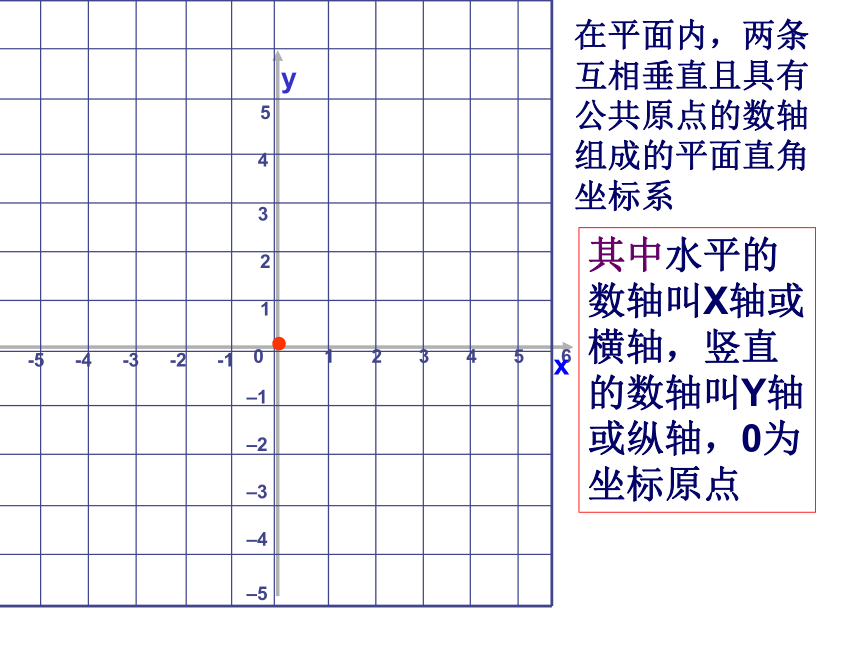
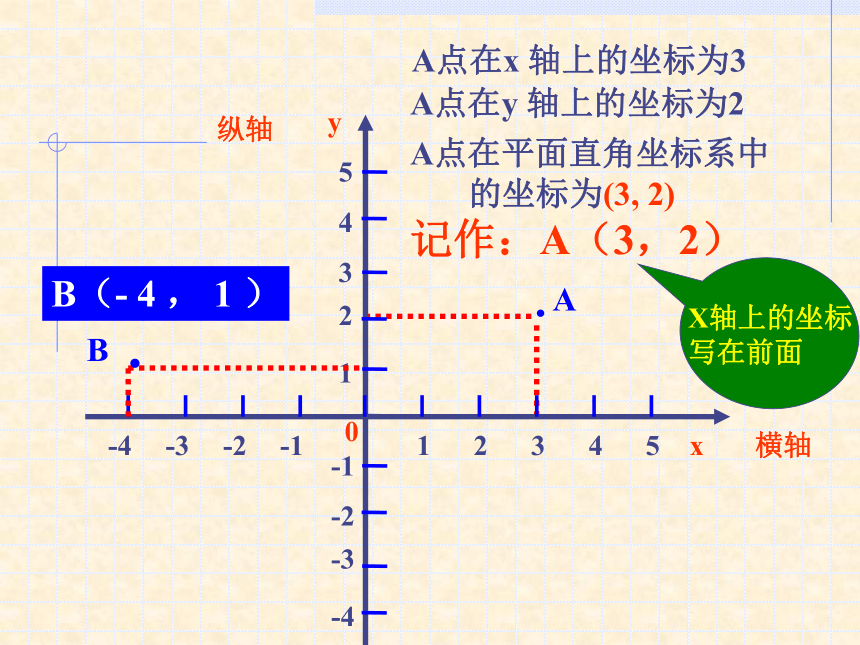
关系。1234560–1–2–3–4–512345 yx-6-5-4-3-2-1在平面内，两条互相垂直且具有公共原点的数轴组成的平面直角坐标系其中水平的数轴叫X轴或横轴，竖直的数轴叫Y轴或纵轴，0为坐标原点·AA点在x 轴上的坐标为3A点在y 轴上的坐标为2A点在平面直角坐标系中
的坐标为(3, 2)
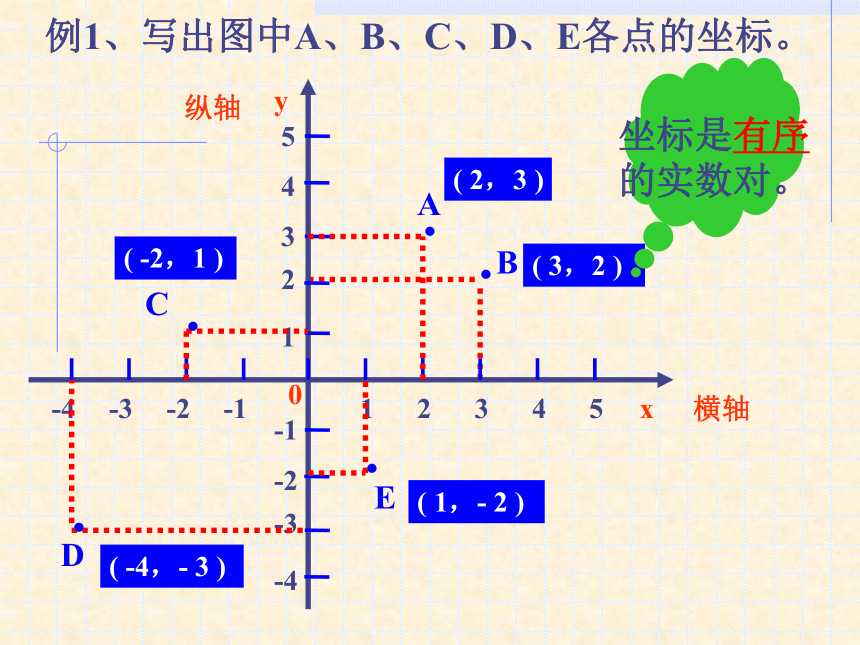
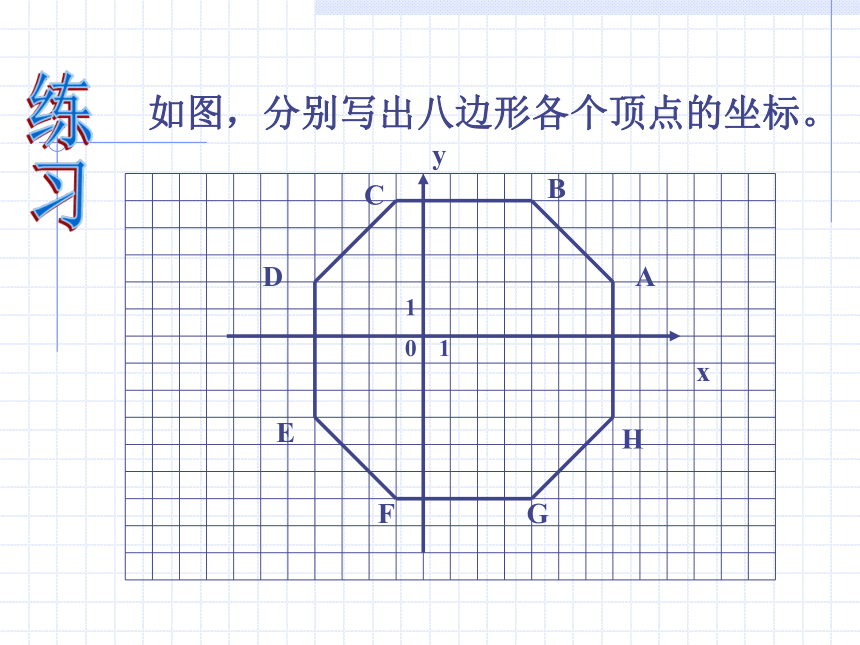
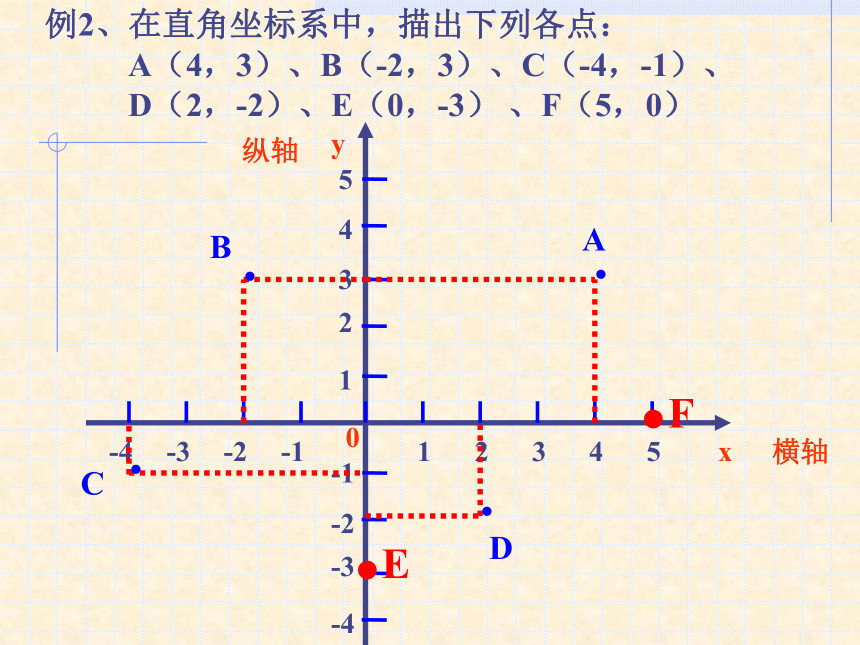
记作：A（3，2）B（- 4 ， 1 ）·B·C·A·E·D( 2，3 )( 3，2 )( -2，1 )( -4，- 3 )( 1，- 2 )例1、写出图中A、B、C、D、E各点的坐标。如图，分别写出八边形各个顶点的坐标。练习例2、在直角坐标系中，描出下列各点：
A（4，3）、B（-2，3）、C（-4，-1）、
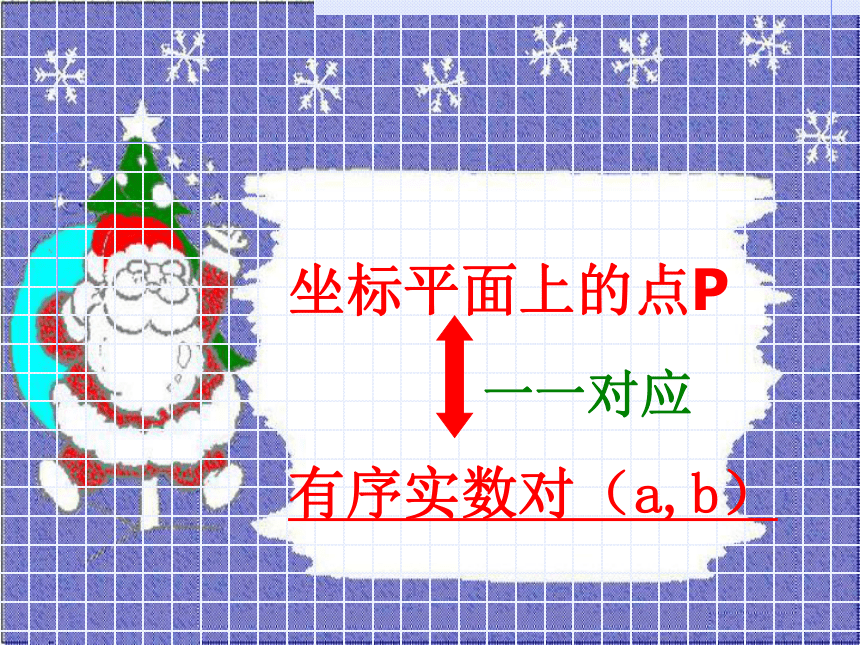
D（2，-2）、E（0，-3） 、F（5，0） .E.F 如果给你一对有序实数对（可能是整数，可能是分数，也可能是无理数），那么你能在直角坐标系中描出它所对应的点吗？ 图形中的一个点，它的坐标可能是整数、分数，可能是无理数吗？坐标平面上的点P
有序实数对（a,b）一一对应这节课我们学习了什么？学习目标了解四个象限的点的符号特征；
能够判断出任意点是属于什么象限；
1234560–1–2–3–4–512345 yx-6-5-4-3-2-1第一象限第四象限第二象限第三象限注 意:
坐标轴上的点不属于任何象限。思考：判断下列各点各属于什么象限？A（3，2），B（3，-1），C（-1，-2）
D（-2,3）你是如何判断出来的呢？思考：满足下列条件的点P（a，b）
具有什么特征？
（1）当点P分别落在第一象限、第二象限、 第三象限、第四象限时横坐标与纵坐标有什么特征？（+，+）（－，+）（－，－）（+，－）xy阶梯训练一第一象限第四象限第三象限第二象限（＋，＋）（－，＋）（－，－）（＋，－）巩固练习：1.点（3，-2）在第_____象限;
点（-1.5，-1）在第_______象限；
点（- ，2）在第_____象限；
点（0，3）在____轴上；
若点（a+1，-5）在y轴上，则a=______；
点（3，0）在_____轴上 2.若点（a,b-1)在第二象限，则a的取值范围是_____，b的取值范围________。四三二y-1xa＜0b＞1思考：满足下列条件的点P（a，b）
具有什么特征？
（2）当点P落在X轴、Y轴上呢？
点P落在原点上呢？xy阶梯训练一·（0，b）P（a，0）任何一个在 x轴上的点
的纵坐标都为0。 任何一个在 y轴上的点的横坐标都为0。A(3,1), B(1,0), C(2,-1), D(0,2),E(0,0)，
F（0，-3）
以上六个点有多少个是在横轴上的点？
纵轴上的呢？
原点既属于X轴，也属于Y轴例3：填空
若点A（a,b）在第三象限，则点 Q
(－a+1，b－5)在第（ ）象限。
2. 若点B（m+4,m－1)在X轴上，则m=______。
3. 若点 C(x,y)满足x+y<0 , xy >0 ，
则点C在第（ ）象限。1三学习目标1，能够求出任意点关于x轴对称的点的坐标；
2，能够求出任意点关于y轴对称的点的坐标；
3，能够求出任意点关于原点对称的点的坐标；
点P到x轴的距离是多少？
到y轴的距离是多少？在坐标系中描出点P（4，-3）点p到x轴的距离是3个单位长度；点p到y轴的距离是4个单位长度.a>0,b>0,点（a，b）到x轴的距离是？到y轴距离是？点（a，b）到x轴的距离是b个单位长度；
点（a，b）到y轴的距离是a个单位长度思考练习：
1.点 M（- 8，12）到 x轴的距离_________，
到 y轴的距离是________.
2.点K（0.5，1）到x轴的距离是_________,
到y轴的距离是 —————。
3.若点P在第三象限，且到x轴的距离_______ ，
到y轴的距离为1.5，则点P的坐标是________。
点P（4，-3）关于X 轴对称的点的坐标是：
关于Y 轴对称的点的坐标是：
关于原点对称的点的坐标是：（4，3）（-4，-3）（-4，3）思考在坐标系中描出点P（4，-3）点P（a，b）关于X 轴对称的点的坐标是：
关于Y 轴对称的点的坐标是：
关于原点对称的点的坐标是：（a，-b）（-a，b）（-a，-b）阶梯训练二点A（2，-3）
关于x轴对称的点是点（ ， ）；
关于y轴对称的点是点______ ;
关于原点对称的点是点_______;
点B（ ，1 ）
关于原点对称的点是点______;
关于纵轴对称的点是点______.
例4：
⑴已知点P1(a，3)与点P2(-2，b)关于
Y轴对称，则a=( ),b=( )⑵已知点P1(a，3)与点P2(-2，b)关于
X轴对称，则a=( ),b=( )⑶已知点P1(a，3)与点P2(-2，b)关于
原点对称，则a=( ),b=( )2 3-2 -3 2 -3例1:写出下图中的多边形ABCDEF各个顶点的坐标。D解：如图，各个顶点的坐标分别为：
A(-2,0) B(0,-3)
C(3,-3) D(4,0)
E(3,3) F(0,3)
(-2,0)(0,-3)(3,-3)D(4,0)(3,3)(0,3)想一想：1、点B与点C的纵坐标有什么关系，线段BC的位置有什么特点？
2、点E与点C的坐标有什么特点？线段CE的位置有什么特点？1：纵坐标相等；
线段BC平行于横轴，垂直于纵轴；2：横坐标相等；
线段CE平行于纵轴，垂直于横轴；xy学习目标学会建立适当的平面直角坐标系·m（5，4）例1, 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标. BCDA解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
做一做xy0(0 , 0 )( 0 , 4 )( 6 , 4 )( 6 , 0)由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
C议一议你还可以怎样建立直角坐标系呢？ 解：如图：以CD所在的直线为X轴，以线段CD的中垂线为Y轴，建立直角坐标系。由CD 的长6，此时的点C的坐标为（-3，0）， D（3，0） CB的长为4，可以得到B，A的坐标为，B（-3，4），A（3，4）联想ABC0例3.对于边长为4的正三角形△ABC，建立适当的直角坐标系，写出各个顶点的坐标思考：怎样求出A的纵坐标呢？A（0，2 3），B（-2，0）
C（2，0）AO=16-4=2 3X练习：P159随堂练习考考你在一次“寻宝”游戏中,寻宝人已经找到了坐标为
( 3 , 2 ) 和( 3 , -2 ) 的两个标志点, 并且知道藏宝
地点的坐标为( 4 , 4 ),除此外不知道其他信息,
如何确定直角坐标系找的“宝藏”?你能找到吗?
与同伴交流.提示: 连接两个标志点, 作所得线段的中垂线,并以这条线为
横轴.那如何来确定纵轴? 议一议在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此以外不知道其他信息,如何确定直角坐标系找到“宝藏”x123410432–2–1–1–2–3–4–3–4Y56A(3,2)B(-3,2)议一议在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此以外不知道其他信息,如何确定直角坐标系找到“宝藏”x123410432–2–1–1–2–3–4–3–4Y56A(3,2)B(-3,2)议一议在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此以外不知道其他信息,如何确定直角坐标系找到“宝藏”x123410432–2–1–1–2–3–4–3–4Y56A(3,2)B(-3,2)议一议在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此以外不知道其他信息,如何确定直角坐标系找到“宝藏”x123410432–2–1–1–2–3–4–3–4Y56A(3,2)B(-3,2)议一议在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此以外不知道其他信息,如何确定直角坐标系找到“宝藏”x123410432–2–1–1–2–3–4–3–4Y56A(3,2)B(-3,2)C(4,4)可见：
⑴选取的坐标系不同，同一点的坐标不同；
⑵为使计算简化，证明方便，需要恰当地
选取坐标系；
⑶“恰当”意味着要充分利用图形的特点：
垂直关系、对称关系、平行关系、中点
等。例5：求边长为4的正方形ABCD
的各顶点的坐标思考：满足下列条件的点P（a，b）
具有什么特征？
（3）当点P落在一、三象限的两条坐标轴
夹角平分线上时xy阶梯训练一（a，a）a=b思考：满足下列条件的点P（a，b）
具有什么特征？
（4）当点P落在二、四象限的两条坐标轴
夹角平分线上时
xy阶梯训练一（a，-a）a=－b 本节课我们学习了平面直角坐标系。
学习本节我们要掌握以下三方面的内容：
1、怎样建立平面直角坐标系
2、能在直角坐标系中，根据坐标找出点，
由点求出坐标。
3、坐标平面分为哪几部分？各有什么特征？
4、对称点的坐标有何规律？
作业：P137 1、2（作业本）能力训练 已知边长为 4的正方形 ABCD，在直角坐标系中，C、D两点在第二象限，AB与 X轴的交角为 60°，求C点的坐标。