2022年湘教版数学七年级下册6.1.2 中位数 课时练习(Word版含答案)
文档属性
| 名称 | 2022年湘教版数学七年级下册6.1.2 中位数 课时练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 11:03:15 | ||
图片预览

文档简介
2022年湘教版数学七年级下册
6.1.2《中位数》课时练习
一、选择题
1.某校开展了以“爱我家乡” 为主题的艺术活动,从九年级5个班收集到的艺术作品数量(单位:件)分别为 48,50,47,44,50,则这组数据的中位数是( )
A.44 B.47 C.48 D.50
2.菲尔兹奖是数学领域的一项国际大奖,常被视为数学界的诺贝尔奖,每四年颁发一次,最近一届获奖者获奖时的年龄(单位:岁)分别为:30,40,34,36,则这组数据的中位数是( )
A.34 B.35 C.36 D.40
3.喜迎建党 100 周年,某校将举办小合唱比赛,七个参赛小组人数如下:5,5,6,7,x,7,8.已知这组数平均数是6,则这组数据的中位数( )
A.5 B.5.5 C.6 D.7
4.某班九个合作学习小组的人数分别为5,5,5,6,,7,7,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.7 B.6 C.5. 5 D.5
5.中国奥运冠军朱启南在亚运会男子10米气步枪决赛中,凭借最后3枪的出色发挥,以总成绩702.2环夺得冠军。他在决赛中打出的10枪成绩(单位:环)是:10.4,9.6,10.4,10.1,10.2,10.7,10.2,10.5,10.7,10.4.则这组数据的中位数是( )
A.10.7 B.10.4 C.10.3 D.10.2
6.孔晓东同学在“低碳黄冈 绿色未来”演讲比赛中,6位评委给他的打分如下表:
评委代号 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ
评 分 85 90 80 95 90 90
则他得分的中位数为( )
A.95 B.90 C.85 D.80
7.已知一组数据3、4、4、5、6、7、4、7,那么这组数据的( )
A.中位数是5.5,众数是4
B.中位数是5,平均数是5
C.中位数是5,众数是4
D.中位数是4.5,平均数是5
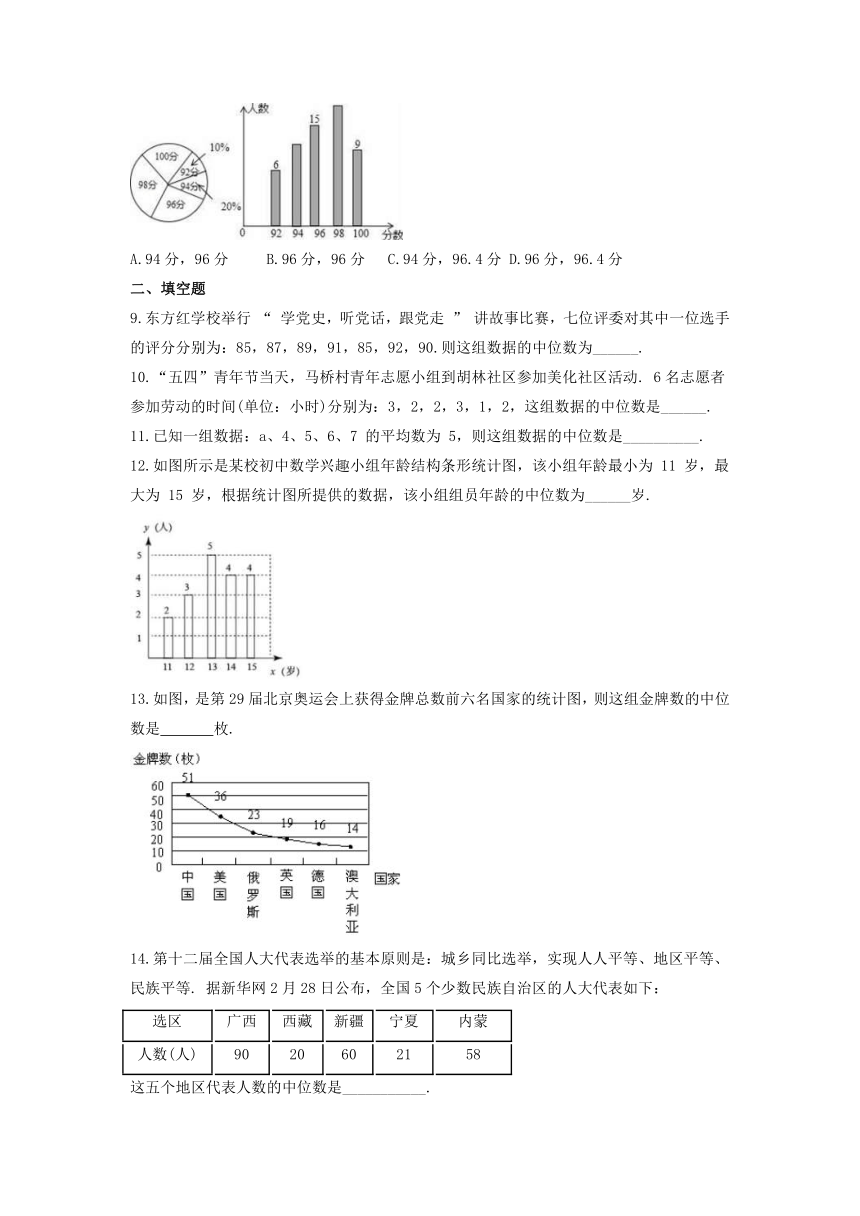
8.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
A.94分,96分 B.96分,96分 C.94分,96.4分 D.96分,96.4分
二、填空题
9.东方红学校举行 “ 学党史,听党话,跟党走 ” 讲故事比赛,七位评委对其中一位选手的评分分别为:85,87,89,91,85,92,90.则这组数据的中位数为______.
10.“五四”青年节当天,马桥村青年志愿小组到胡林社区参加美化社区活动. 6名志愿者参加劳动的时间(单位:小时)分别为:3,2,2,3,1,2,这组数据的中位数是______.
11.已知一组数据:a、4、5、6、7 的平均数为 5,则这组数据的中位数是__________.
12.如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为 11 岁,最大为 15 岁,根据统计图所提供的数据,该小组组员年龄的中位数为______岁.
13.如图,是第29届北京奥运会上获得金牌总数前六名国家的统计图,则这组金牌数的中位数是 枚.
14.第十二届全国人大代表选举的基本原则是:城乡同比选举,实现人人平等、地区平等、民族平等. 据新华网2月28日公布,全国5个少数民族自治区的人大代表如下:
选区 广西 西藏 新疆 宁夏 内蒙
人数(人) 90 20 60 21 58
这五个地区代表人数的中位数是___________.
三、解答题
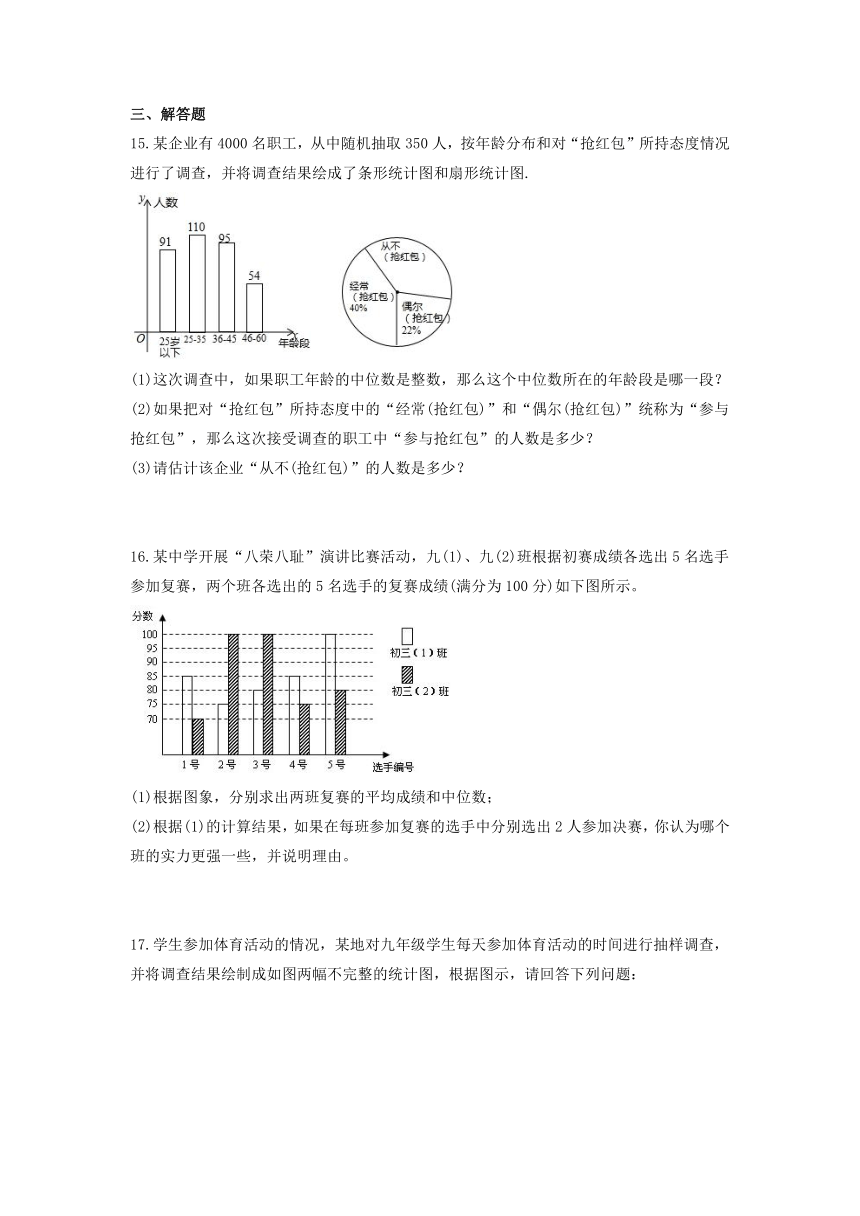
15.某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?
(3)请估计该企业“从不(抢红包)”的人数是多少?
16.某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据图象,分别求出两班复赛的平均成绩和中位数;
(2)根据(1)的计算结果,如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,并说明理由。
17.学生参加体育活动的情况,某地对九年级学生每天参加体育活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)求被抽样调查的学生总数和每天体育活动时间为1.5小时的学生数。
(2)每天体育活动时间的中位数;
(3)该校共有3500名学生,请估计该地九年级每天体育活动时间超过1小时的学生有多少人
18.在同一条件下,对同一型号的汽车进行耗油1升所行驶路程的实验,将收集到的数据作为一个样本进行分析,绘制出部分频数分布直方图和部分扇形统计图.如下图所示(路程单位:km)
结合统计图完成下列问题:
(1)扇形统计图中,表示12.5≤x<13部分的百分数是 ;
(2)请把频数分布直方图补充完整,这个样本数据的中位数落在第 组;
(3)哪一个图能更好地说明一半以上的汽车行驶的路程在13≤x<14之间?哪一个图能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车?
参考答案
1.答案为:C.
2.答案为:B.
3.答案为:C.
4.答案为:B
5.答案为:B
6.答案为:B.
7.答案为:D
8.答案为:D.
9.答案为:89.
10.答案为:2.
11.答案为:5.
12.答案为:13
13.答案为:21
14.答案为:58.
15.解:(1)∵抽取350人,∴中位数是175和176的平均数,
∴中位数所在的年龄段是25-35;
(2)这次接受调查的职工中“参与抢红包”的人数是:350×(40%+22%)=217人;
(3)估计该企业“从不(抢红包)”的人数是:4000×(1-40%-22%)=1520人.
16.解:(1)九(1)平均数80分,中位数85分,九(2)平均数80分,中位数80分
(2)∵九(1)班、九(2)班前两名选手的平均分分别为92.5,100分,
∴在每班参加复赛的选手中分别选出2人参加决赛,九(2)班的实力更强一些。
17.解:(1)被调查的学生总数有500人,每天体育活动时间为1.5小时的学生数为120人
(2)中位数为1
(3)该地九年级每天体育活动时间超过1小时的学生为1400人
18.解:(1)1﹣13.3%﹣6.7%﹣30%﹣30%=20%;
(2)第2组的频数=30×20%=6,如图:
样本数据的中位数落在第3组;
(3)扇形统计图能很好地说明一半以上的汽车行驶的路程在13≤x<14之间;条形统计图(或直方统计图)能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车.
6.1.2《中位数》课时练习
一、选择题
1.某校开展了以“爱我家乡” 为主题的艺术活动,从九年级5个班收集到的艺术作品数量(单位:件)分别为 48,50,47,44,50,则这组数据的中位数是( )
A.44 B.47 C.48 D.50
2.菲尔兹奖是数学领域的一项国际大奖,常被视为数学界的诺贝尔奖,每四年颁发一次,最近一届获奖者获奖时的年龄(单位:岁)分别为:30,40,34,36,则这组数据的中位数是( )
A.34 B.35 C.36 D.40
3.喜迎建党 100 周年,某校将举办小合唱比赛,七个参赛小组人数如下:5,5,6,7,x,7,8.已知这组数平均数是6,则这组数据的中位数( )
A.5 B.5.5 C.6 D.7
4.某班九个合作学习小组的人数分别为5,5,5,6,,7,7,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.7 B.6 C.5. 5 D.5
5.中国奥运冠军朱启南在亚运会男子10米气步枪决赛中,凭借最后3枪的出色发挥,以总成绩702.2环夺得冠军。他在决赛中打出的10枪成绩(单位:环)是:10.4,9.6,10.4,10.1,10.2,10.7,10.2,10.5,10.7,10.4.则这组数据的中位数是( )
A.10.7 B.10.4 C.10.3 D.10.2
6.孔晓东同学在“低碳黄冈 绿色未来”演讲比赛中,6位评委给他的打分如下表:
评委代号 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ
评 分 85 90 80 95 90 90
则他得分的中位数为( )
A.95 B.90 C.85 D.80
7.已知一组数据3、4、4、5、6、7、4、7,那么这组数据的( )
A.中位数是5.5,众数是4
B.中位数是5,平均数是5
C.中位数是5,众数是4
D.中位数是4.5,平均数是5
8.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
A.94分,96分 B.96分,96分 C.94分,96.4分 D.96分,96.4分
二、填空题
9.东方红学校举行 “ 学党史,听党话,跟党走 ” 讲故事比赛,七位评委对其中一位选手的评分分别为:85,87,89,91,85,92,90.则这组数据的中位数为______.
10.“五四”青年节当天,马桥村青年志愿小组到胡林社区参加美化社区活动. 6名志愿者参加劳动的时间(单位:小时)分别为:3,2,2,3,1,2,这组数据的中位数是______.
11.已知一组数据:a、4、5、6、7 的平均数为 5,则这组数据的中位数是__________.
12.如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为 11 岁,最大为 15 岁,根据统计图所提供的数据,该小组组员年龄的中位数为______岁.
13.如图,是第29届北京奥运会上获得金牌总数前六名国家的统计图,则这组金牌数的中位数是 枚.
14.第十二届全国人大代表选举的基本原则是:城乡同比选举,实现人人平等、地区平等、民族平等. 据新华网2月28日公布,全国5个少数民族自治区的人大代表如下:
选区 广西 西藏 新疆 宁夏 内蒙
人数(人) 90 20 60 21 58
这五个地区代表人数的中位数是___________.
三、解答题
15.某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?
(3)请估计该企业“从不(抢红包)”的人数是多少?
16.某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据图象,分别求出两班复赛的平均成绩和中位数;
(2)根据(1)的计算结果,如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,并说明理由。
17.学生参加体育活动的情况,某地对九年级学生每天参加体育活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)求被抽样调查的学生总数和每天体育活动时间为1.5小时的学生数。
(2)每天体育活动时间的中位数;
(3)该校共有3500名学生,请估计该地九年级每天体育活动时间超过1小时的学生有多少人
18.在同一条件下,对同一型号的汽车进行耗油1升所行驶路程的实验,将收集到的数据作为一个样本进行分析,绘制出部分频数分布直方图和部分扇形统计图.如下图所示(路程单位:km)
结合统计图完成下列问题:
(1)扇形统计图中,表示12.5≤x<13部分的百分数是 ;
(2)请把频数分布直方图补充完整,这个样本数据的中位数落在第 组;
(3)哪一个图能更好地说明一半以上的汽车行驶的路程在13≤x<14之间?哪一个图能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车?
参考答案
1.答案为:C.
2.答案为:B.
3.答案为:C.
4.答案为:B
5.答案为:B
6.答案为:B.
7.答案为:D
8.答案为:D.
9.答案为:89.
10.答案为:2.
11.答案为:5.
12.答案为:13
13.答案为:21
14.答案为:58.
15.解:(1)∵抽取350人,∴中位数是175和176的平均数,
∴中位数所在的年龄段是25-35;
(2)这次接受调查的职工中“参与抢红包”的人数是:350×(40%+22%)=217人;
(3)估计该企业“从不(抢红包)”的人数是:4000×(1-40%-22%)=1520人.
16.解:(1)九(1)平均数80分,中位数85分,九(2)平均数80分,中位数80分
(2)∵九(1)班、九(2)班前两名选手的平均分分别为92.5,100分,
∴在每班参加复赛的选手中分别选出2人参加决赛,九(2)班的实力更强一些。
17.解:(1)被调查的学生总数有500人,每天体育活动时间为1.5小时的学生数为120人
(2)中位数为1
(3)该地九年级每天体育活动时间超过1小时的学生为1400人
18.解:(1)1﹣13.3%﹣6.7%﹣30%﹣30%=20%;
(2)第2组的频数=30×20%=6,如图:
样本数据的中位数落在第3组;
(3)扇形统计图能很好地说明一半以上的汽车行驶的路程在13≤x<14之间;条形统计图(或直方统计图)能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车.
