1.3.2球的表面积和体积课件
文档属性
| 名称 | 1.3.2球的表面积和体积课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 372.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-25 00:00:00 | ||
图片预览






文档简介
课件17张PPT。湖南省耒阳市振兴学校
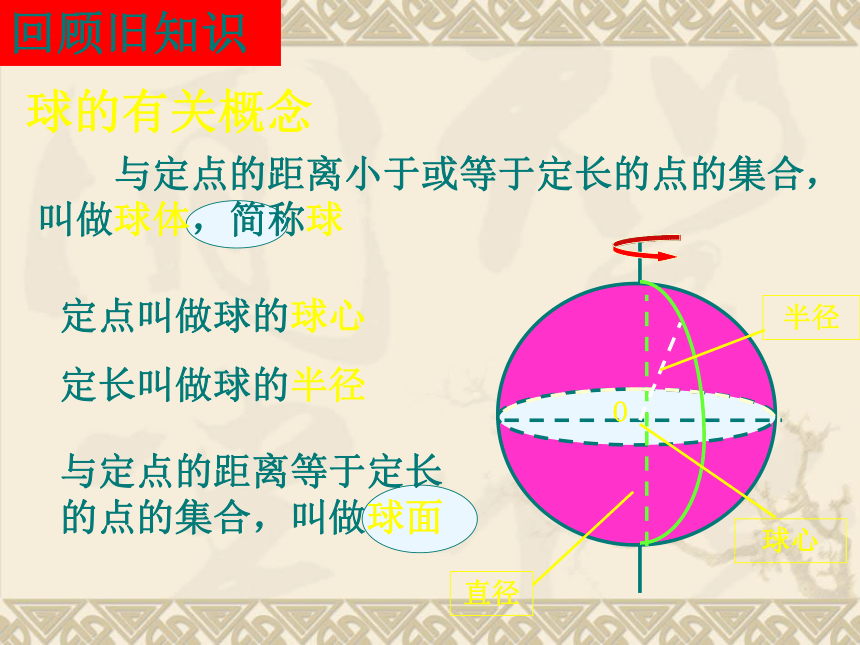
欧阳文丰老师制作--球的体积和表面积--掌握球的体积、表面积公式.会用球的表面积公式、体积公式解决相关问题,培养学生应用数学的能力.能解决球的截面有关计算问题及球的“内接”与“外切”的几何体问题.教学目标球的截面有关计算问题球的体积公式及应用球的表面积公式及应用球的“内接”与“外切”的几何体问题教学重点教学难点重点难点 与定点的距离小于或等于定长的点的集合,叫做球体,简称球回顾旧知识球的有关概念定点叫做球的球心
定长叫做球的半径与定点的距离等于定长的点的集合,叫做球面1、 球的表面积思考:经过球心的截面圆面积是什么?它与球的表面积有什么关系? 定理:半径为R的球的表面积是
球的表面积等于球的大圆面积的4倍学习新知识2、 球的体积定理:半径为R的球的体积是
学习新知识例4、如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积.
(2)球的表面积等于圆柱全面积的三分之二.
证明:(2)例题讲解4.若两球体积之比是1:2,则其表面积之比是______.练习一1.若球的表面积变为原来的2倍,则半径变为原来的___倍.2.若球半径变为原来的2倍,则表面积变为原来的___倍.3.若两球表面积之比为1:2,则其体积之比是______.课堂练习6.将半径为1和2的两个铅球,熔成一个大铅球,那么
这个大铅球的表面积是______.5.若两球表面积之差为48π ,它们大圆周长之和为12π ,
则两球的直径之差为______.练习二课堂练习补充练习 1、有一种空心钢球,质量为142g,测得
外径等于5.0cm,求它的内径(钢
的密度为7.9g/cm3,精确到0.1cm).补充练习 2、长方体的一个顶点上三条棱长分别为3、4、5,若它的八个顶点都在同一球面上,则这个球的表面积是—— 分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们中心重合,则长方体对角线与球的直径相等。222211504 42+5)2(:RS2R=3RDDBRt ppD==+=中略解:
3、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。 解:作出过一条侧棱PC和高PO的截面,则截面三角形PDC的边PD是斜高,DC是斜高的射影,球被截成的大圆与DP、DC相切,连结EO,设球半径为r,
3、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。解法2:连结OA、OB、OC、OP,那么
解题小结:1、多面体的“切”、“接”问题,必须明确“切”、“接”位置和有关元素间的数量关系,常借助“截面”图形来解决。2、正三棱锥、正四面体是重要的基本图形,要掌握其中的边、角关系。能将空间问题化为平面问题得到解决,并注意方程思想的应用。3、正四面体的内切球半径等于其高的四分之一,外接球半径等于其高的四分之三。课后练习1、正方体的内切球和外接球体积比为___ ___ ,表面积比为 。 (答案: , 1:3.)
2、在球心同侧有相距9cm的两个平行截面,它们的面积分别为49 和400 ,求球的表面积。
答案:25001、有关球和球面的概念。2、熟练掌握球的体积、表面积公式:归纳与小结3、球的体积公式和表面积的一些运用。布置作业教材P30习题1.3B组3.谢谢!再见!
欧阳文丰老师制作--球的体积和表面积--掌握球的体积、表面积公式.会用球的表面积公式、体积公式解决相关问题,培养学生应用数学的能力.能解决球的截面有关计算问题及球的“内接”与“外切”的几何体问题.教学目标球的截面有关计算问题球的体积公式及应用球的表面积公式及应用球的“内接”与“外切”的几何体问题教学重点教学难点重点难点 与定点的距离小于或等于定长的点的集合,叫做球体,简称球回顾旧知识球的有关概念定点叫做球的球心
定长叫做球的半径与定点的距离等于定长的点的集合,叫做球面1、 球的表面积思考:经过球心的截面圆面积是什么?它与球的表面积有什么关系? 定理:半径为R的球的表面积是
球的表面积等于球的大圆面积的4倍学习新知识2、 球的体积定理:半径为R的球的体积是
学习新知识例4、如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积.
(2)球的表面积等于圆柱全面积的三分之二.
证明:(2)例题讲解4.若两球体积之比是1:2,则其表面积之比是______.练习一1.若球的表面积变为原来的2倍,则半径变为原来的___倍.2.若球半径变为原来的2倍,则表面积变为原来的___倍.3.若两球表面积之比为1:2,则其体积之比是______.课堂练习6.将半径为1和2的两个铅球,熔成一个大铅球,那么
这个大铅球的表面积是______.5.若两球表面积之差为48π ,它们大圆周长之和为12π ,
则两球的直径之差为______.练习二课堂练习补充练习 1、有一种空心钢球,质量为142g,测得
外径等于5.0cm,求它的内径(钢
的密度为7.9g/cm3,精确到0.1cm).补充练习 2、长方体的一个顶点上三条棱长分别为3、4、5,若它的八个顶点都在同一球面上,则这个球的表面积是—— 分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们中心重合,则长方体对角线与球的直径相等。222211504 42+5)2(:RS2R=3RDDBRt ppD==+=中略解:
3、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。 解:作出过一条侧棱PC和高PO的截面,则截面三角形PDC的边PD是斜高,DC是斜高的射影,球被截成的大圆与DP、DC相切,连结EO,设球半径为r,
3、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。解法2:连结OA、OB、OC、OP,那么
解题小结:1、多面体的“切”、“接”问题,必须明确“切”、“接”位置和有关元素间的数量关系,常借助“截面”图形来解决。2、正三棱锥、正四面体是重要的基本图形,要掌握其中的边、角关系。能将空间问题化为平面问题得到解决,并注意方程思想的应用。3、正四面体的内切球半径等于其高的四分之一,外接球半径等于其高的四分之三。课后练习1、正方体的内切球和外接球体积比为___ ___ ,表面积比为 。 (答案: , 1:3.)
2、在球心同侧有相距9cm的两个平行截面,它们的面积分别为49 和400 ,求球的表面积。
答案:25001、有关球和球面的概念。2、熟练掌握球的体积、表面积公式:归纳与小结3、球的体积公式和表面积的一些运用。布置作业教材P30习题1.3B组3.谢谢!再见!
