3.3机械波案例分析 课时提升练(word版含答案)
文档属性
| 名称 | 3.3机械波案例分析 课时提升练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 915.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-07 19:43:28 | ||
图片预览




文档简介
3.3机械波案例分析 课时提升练(含解析)
一、选择题
1.一列简谐横波沿x轴传播,已知x轴上x1=1m和x2=4m处质点的振动图像如图甲、图乙所示,则此列波的传播速度不可能是( )
A.0.6m/s B.1m/s C.2m/s D.3m/s
2.如图(a)所示,一列简谐横波沿x轴传播,实线和虚线分别为t1时刻和t2时刻的波形图,其中t2>t1,P、Q分别是平衡位置为x1=1.0m和x2=4.0 m的两质点。图(b)为质点Q的振动图像,下列说法正确的是( )
A.t2-t1=0.1s
B.t2时刻Q的速度达到最大
C.简谐横波沿x轴传播的速度大小为40m/s
D.t1到t2内,P、Q运动的路程相等
3.在均匀介质绳中选取平衡位置在同一直线上的9个质点,相邻两质点的距离均为1m,如图(a)所示,一列简谐横波沿该直线向右传播,t=0时刚到达质点1,质点1开始向下运动,6s后第一次出现如图(b)所示的波形。对于该列波下列说法正确的是( )
A.周期T=6s B.波长=9m
C.波速=2m/s D.频率f=0.5Hz
4.一列简谐横波在t=s时的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图像。下列表述正确的是( )
A.这列波的传播方向为沿着x轴正方向
B.t=2 s时质点P的加速度方向沿着y轴负方向
C.这列波的传播速度大小为9 cm/s
D.质点Q的平衡位置横坐标为9 cm
5.一列简谐横波沿x轴传播,t=0.1s时的波形图如图甲所示,A、B为介质中的两质点。图乙为质点A的振动图像。以下判断正确的是( )
A.t=0.15s时,A的加速度为零
B.t=0.15s时,B的速度沿y轴正方向
C.从t=0.1s到t=0.25s,B的位移大小为10cm
D.从t=0.1s到t=0.25s,波沿x轴负方向传播了7.5m
6.图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x1=1m处的质点。Q是平衡位置为x2=4m处的质点,图乙为质点Q的振动图像,则( )
A.时,质点Q的加速度方向沿y轴负方向
B.该波沿x轴负方向传播,传播速度大小为20m/s
C.再经过0.10 s,质点Q沿波的传播方向移动4m
D.,质点P的位移是
7.图甲是一列简谐横波传播到x=5m的M点时的波形图,图乙是波形图上某质点从此时刻开始计时的振动图像,是位于x=10m处的质点,下列说法正确的是( )
A.乙图可能是x=1m处质点的振动图像 B.当点开始振动时,M点位于波谷
C.当点处于波峰时,N点的位移为0 D.经过3s,M点运动到x=8m处
8.图甲为一简谐横波在时刻的波形图像,图乙为横波中处质点的振动图像,下列说法正确的是( )
A.波的传播方向沿轴负方向
B.波的传播速度大小为0.01m/s
C.在时刻,质点的振动速度大小为0
D.在时刻,质点的振动加速度大小为0
9.如图所示,图甲为一列沿x轴传播的简谐横波在某时刻的波形图,P为平衡位置在的质点,图乙为此波中平衡位置坐标的质点从该时刻起的振动图像,下列说法中正确的是( )
A.波沿x轴负方向传播
B.由甲、乙两图可知该波波速为
C.从该时刻起,时,P点刚好经过平衡位置,振动方向向下
D.从该时刻起,P点第一次回到平衡位置通过的路程是
10.一列简谐横波沿x轴正方向传播,时波形如图所示。已知质点P再经过0.1s第一次到达波谷处,下列说法正确的是( )
A.这列简谐横波的波长是5m
B.这列简谐横波的波速是10m/s
C.质点Q要再经过0.2s才能第一次到达波峰处
D.质点Q到达波峰时质点P也恰好到达波峰
11.一列向右传播的横波在t=0时的波形如图所示,A、B两质点间距为8m,B、C两质点平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,该波的波速可能为( )
A.9m/s B.10m/s C.11m/s D.12m/s
12.一列简谐横波沿x轴传播,在t=0时刻的图像如图甲所示,介质中P质点的振动图像如图乙所示,下列说法正确的是( )
A.波沿x轴正方向传播
B.介质中质点振动周期为2s
C.波速大小为m/s
D.在t=2.5s时刻P、Q两质点的速度相同
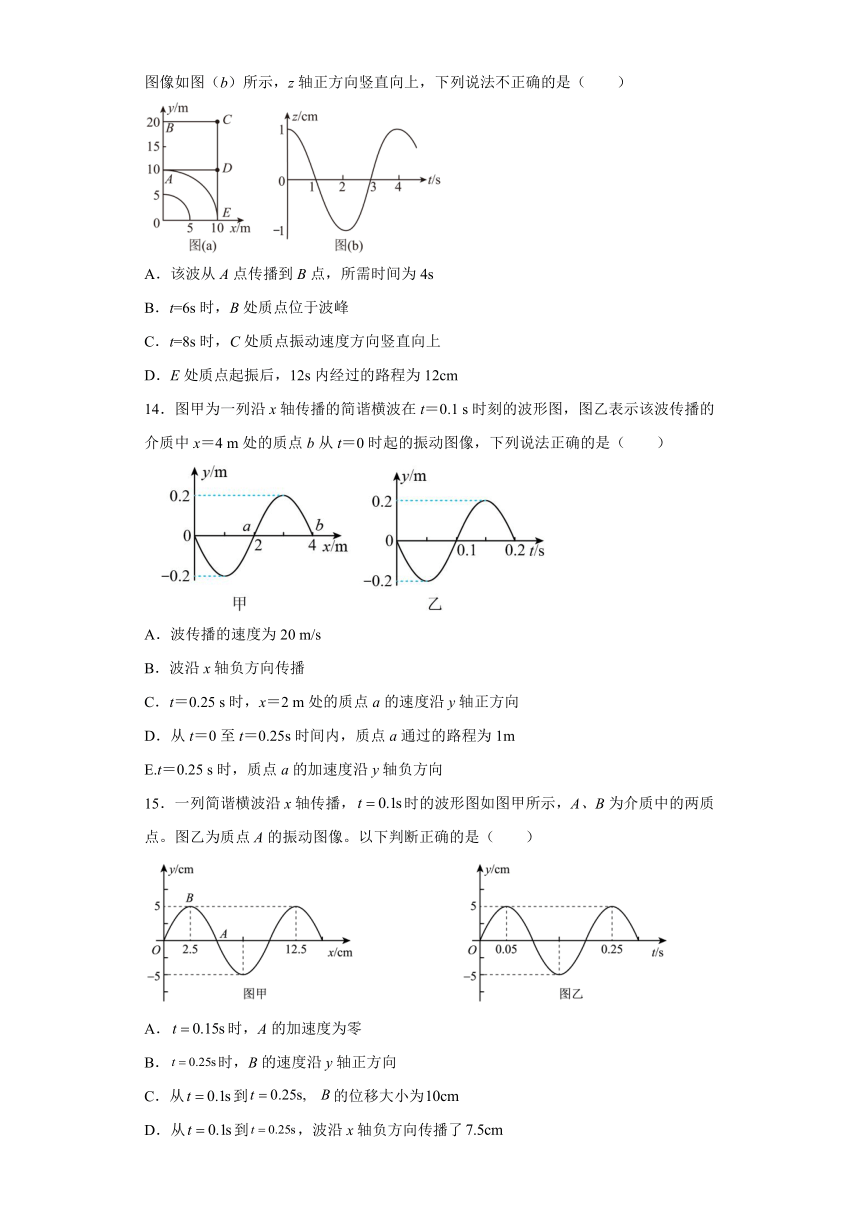
13.均匀介质中,波源位于O点的简谐横波在xOy水平面内传播,波面为圆。t=0时刻,波面分布如图(a)所示,其中实线表示波峰,虚线表示相邻的波谷,A处质点的振动图像如图(b)所示,z轴正方向竖直向上,下列说法不正确的是( )
A.该波从A点传播到B点,所需时间为4s
B.t=6s时,B处质点位于波峰
C.t=8s时,C处质点振动速度方向竖直向上
D.E处质点起振后,12s内经过的路程为12cm
14.图甲为一列沿x轴传播的简谐横波在t=0.1 s时刻的波形图,图乙表示该波传播的介质中x=4 m处的质点b从t=0时起的振动图像,下列说法正确的是( )
A.波传播的速度为20 m/s
B.波沿x轴负方向传播
C.t=0.25 s时,x=2 m处的质点a的速度沿y轴正方向
D.从t=0至t=0.25s时间内,质点a通过的路程为1m
E.t=0.25 s时,质点a的加速度沿y轴负方向
15.一列简谐横波沿x轴传播,时的波形图如图甲所示,A、B为介质中的两质点。图乙为质点A的振动图像。以下判断正确的是( )
A.时,A的加速度为零
B.时,B的速度沿y轴正方向
C.从到的位移大小为
D.从到,波沿x轴负方向传播了
二、解答题
16.图甲为一简谐横波在t1=0.3 s时刻的波形图,图中M、N两点的平衡位置坐标分别为:xM=1 m,xN=5 m,此时波传到N点,平衡位置坐标x=1 m的质点M振动的图像如图乙所示,质点Q(图中未标出)的平衡位置距O点10 m。求:
(1)该波的波速;
(2)从t=0时刻开始计时,Q点位于波谷的时刻。
17.如图甲所示为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图。已知x=1m处的质点做简谐运动的图象如图乙所示。
(1)求波传播的速度大;
(2)从t=0时刻开始经过多长时间位于x=5m处的质点P开始振动?并求出在0~20s内质点P运动的路程。
参考答案
1.C
【详解】
当该列波向左传播时,根据题干可知1m和4m之间的距离满足的关系为
则由可得波速为
当n=0时,可得;当n=1时可得;
当波向右做传播时1m和4m之间的距离关系满足
则
当n=0时可得;当n=1时可得。故ABD正确,C错误。
本题选不可能的,故选C。
2.C
【详解】
A.因为没有说明t1时刻是哪个时刻,假设t1=0,根据图(b)可知,质点Q在t1时刻正在沿y轴正方向振动,则波向x轴正方向传播,可得
假设t1=0.1s,根据图(b)可知,质点Q在t1时刻正在沿y轴负方向振动,则波向x轴负方向传播,同理可得
故A错误;
B.由A分析可知,无论是哪种情况,t2时刻质点Q都在波峰,振动速度等于零,最小,故B错误;
C.由图可看出波长为8m,周期为0.2s,则波速为
故C正确;
D.t1到t2内, Q运动的路程可能是
或
如果t1=0,在第一个时间内,P沿y轴负方向运动到与x轴对称的位置,路程y1大于振幅A,则t1到t2内的路程
同理如果t1=0.1s,在第一个时间内,P沿y轴正方向运动到波峰,又沿y轴负方向回到原位置,路程y2小于振幅A,则t1到t2内的路程
可知P、Q运动的路程不相等,故D错误。
故选C。
3.C
【详解】
A.横波沿该直线向右传播,图示时刻质点9的振动方向向上,由题波源1的起振动方向向下,则第一次出现如图(b)所示的波形,振动传到质点9后,又传播了周期,则
解得
故A错误;
B.根据图(b)可读出波长为
故B错误;
C.波速为
故C正确;
D.频率为
故选C。
4.D
【详解】
A.当t=s时,Q向上振动,结合题图(a)可知,该波沿x轴负方向传播,故A错误;
B.t=2s时质点P处于平衡位置下方,其加速度方向沿着y轴正方向,故B错误;
C.由题图(a)可以看出,该波的波长λ=36 cm,由题图(b)可以看出周期为T=2 s,故波速为
v==18 cm/s
故C错误;
D.设质点P、Q的平衡位置的x轴分别为xP、xQ,由题图(a)可知,x=0处
y=-=Asin (-30°)
因此
xP=λ=3 cm
由题图(b)可知,在t=0时Q点处于平衡位置,经过Δt=s,其振动状态向x轴负方向传播到P点处,所以
xQ-xP=vΔt=6 cm
解得质点Q的平衡位置的x坐标为
xQ=9 cm
故D正确。
故选D。
5.D
【详解】
A.由题图乙可知,t=0.15s时,质点A处于波谷位置,则此时A的加速度最大,故A错误;
B.由题图乙可知在t=0.1s时质点A处于平衡位置且向下振动,由同侧法结合题图甲可知,波沿x轴负方向传播,由题图乙可知,波的周期为0.20s,则从题图甲所示t=0.1s时开始经过0.05s即个周期质点B处于平衡位置,速度方向沿y轴负方向,故B错误;
C.从t=0.1s到t=0.25s经历了个周期,质点B处于平衡位置,则B的位移为0,故C错误;
D.由题图甲可知,波长λ=10m,由题图乙可知,波的周期为0.20s,则波速为
v==m/s=50m/s
从t=0.1s到t=0.25s,波沿x轴负方向传播了
s=50×0.15m=7.5m
故D正确。
故选D。
6.D
【详解】
A.从乙图可以看出,时,质点Q的加速度方向沿y轴正方向,故A错误;
B. t=0.10s时刻Q沿y轴负方向运动,所以甲图中的波形向左传播,波速为
故B错误;
C.质点在平衡位置往复运动,不随波移动,故C错误;
D.由Q质点的振动图象可得其振动y-t关系式为
P比Q质点滞后八分之三周期,所以P质点的振动y-t关系式为:
将代入可得
故D正确。
故选D。
7.C
【详解】
A.由甲图可知,简谐横波沿x轴正方向传播,此时x=1m处的质点向y轴正方向振动,而乙图t=0时,该质点向y轴负方向振动,故A错误;
B.由甲图可知波长
由乙图可知周期
则波速为
波从M传播到Q的时间
此时M点在平衡位置向y轴正方向振动,经过,M点位于波峰。故B错误;
C.由甲图可知
所以当点处于波峰时,N点的位移为0,故C正确;
D.M点在平衡位置附近振动,不随波迁移,故D错误。
故选C。
8.B
【详解】
A.由图乙可知,时刻,质点向上振动,根据振动方向和波动方向的关系,可以判断出波的传播方向沿轴正方向,故A错误;
B.由图甲可知波长为4cm,由图乙可知周期为4s,波长、周期和波速的关系
故B正确;
C. 在时刻,质点的振动速度为图像的切线,因此速度不为零,故C错误;
D.在时刻,质点处于波峰,加速度最大,故D错误。
故选B。
9.D
【详解】
A.由图乙可知,时刻平衡位置坐标为的质点向下振动,由同侧法可知,该波沿x轴正方向传播,故A错误;
B.由图甲可得
由图乙可得
波速
故B错误;
C.由同侧发法可知,此时P点向上振动,要使P点刚好经过平衡位置,振动方向向下,波需要传播的距离为
所以时间为
可知无论取何值,都不可能等于,故C错误;
D.该波的表达式为
当时
由图可知,0时刻,P点向上振动,P点第一次回到平衡位置通过的路程
故D正确。
故选D。
10.B
【详解】
A.由波形图可知,这列简谐波的波长是4m,故A错误;
B.沿x轴正方向传播,则质点P向y轴负方向运动,由于质点P再经过0.1s第一次到达波谷处,可知波的周期为T=0.4s,则波速为
故B正确;
C.波从图示位置传播到质点Q需要用时
质点Q起振方向沿y轴负方向,从起振到第一次到达波峰需要的时间为t2=0.3s,所以质点Q要再经过0.5s才能第一次到达波峰,故C错误;
D.质点P再过0.5s到达波谷,故D错误。
故选B。
11.A
【详解】
由图可知,波长
波向右传播,质点C恰好通过平衡位置时,波传播的距离可能是或,则波速
或
当时
或
当时
或
故A可能,BCD不可能。
故选A。
12.C
【详解】
A.由题图乙可知,t=0时刻P质点向y轴负方向运动,由题图甲可判断波沿x轴负方向传播,故A错误;
B.设振动周期为T,由图乙可知
解得
T=3s
故B错误;
C.由题图甲可知波长,由波速公式可得波速
故C正确;
D.当P和Q关于平衡位置对称时,即处的质点恰在平衡位置时,P、Q两质点的速度相同,从时刻起,平衡位置的振动状态,向左传播至时处波传播的距离
经历的时间
可得
当n=0时有
t=1.25s
当n=1时有
t=2.75s
故D错误。
故选C。
13.ACD
【详解】
A.由图a可知,
则波长为
由图b可知,周期为
则波速为
因此从A传播到B需要的时间为
A正确;
B.波峰传到B点的时间为4s,该波在t=6s时即再经过,B位于波谷,B错误;
C.t=8s时,即再经过,根据几何关系可知
则
t=8s时,即经过2个周期,C处质点正在向波峰处运动,所有振动速度方向竖直向上,C正确;
D.由于
,
E经过的路程为
D正确。
故选ACD。
14.ADE
【详解】
A.由乙图知,质点的振动周期为T=0.2s,由甲图知,波长λ=4m,则波速为
故A正确;
B.由乙图知,t=0.1s时刻,质点b向上运动,根据甲图可知,该波沿x轴正方向传播,故B错误;
CE.由乙图知,质点的振动周期为T=0.2s,所以质点b在t=0.25s的时刻的振动情况与t=0.05s时刻的振动情况相同,即处于负的最大位移处,而质点a与质点b的间距为半个波长,所以a在正的最大位移处,加速度沿y轴负方向,速度为零,故C错误,E正确;
D.从t=0至t=0.25s时间内,质点a通过的路程为
故D正确。
故选ADE。
15.BD
【详解】
A.由图乙可知,t=0.15s时,质点A处于波谷位置,则此时A的加速度为最大,故A错误;
B.由图乙可知,波的周期为0.20s,则从图甲所示t=0.1s时到t=0.25s经过0.15s即四分之三周期质点B处于平衡位置,速度方向沿y轴正方向,故B正确;
C.从t=0.1s到t=0.25s经历四分之三周期,质点B处于平衡位置,则B的位移为5cm,故C错误;
D.由图乙可知在t=0.1s时质点A处于平衡位置且向下振动,波沿x轴负方向传播,由图甲可知,波长λ=10cm,由图乙可知,波的周期为0.20s,则波速为
从t=0.1s到t=0.25s,波沿x轴负方向传播了
s=50×0.15cm=7.5cm
故D正确。
故选BD。
16.(1) 10 m/s;(2) t=(0.4n+1.1) s,n=0、1、2、3、…
【详解】
(1)据题图甲可知
λ=4 m
据题图乙可得
T=0.4 s
故波速
v==10 m/s
(2)波谷从x=2 m处第一次传播到Q处所需时间
Δt==0.8 s
质点Q第一次到达波谷的时刻为
t′=(0.3+0.8) s=1.1 s
故Q点处于波谷的时刻为
t=(0.4n+1.1) s,n=0、1、2、3、…
17.(1)0.5m/s;(2)6s;28cm
【详解】
(1)由题图乙可知,振幅A=2cm,质点做简谐运动的周期为T=4s,波传播的周期也为T=4s,由题图甲可知波长λ=2m,波速
v==0.5m/s
(2)由题图甲可知,x=2m处的质点在t=0时刻刚好开始沿y轴负方向振动,设再经过Δt时间质点P开始振动,则
Δt==6s
即从t=0时刻开始经过6s时间质点P开始振动,由简谐运动的对称性可知,质点在任意一个全振动过程中的路程
s0=4A=8cm
质点P开始振动后14s内经历了3.5次全振动,所以在0~20s内质点P运动的路程为
s=3.5s0=28cm
一、选择题
1.一列简谐横波沿x轴传播,已知x轴上x1=1m和x2=4m处质点的振动图像如图甲、图乙所示,则此列波的传播速度不可能是( )
A.0.6m/s B.1m/s C.2m/s D.3m/s
2.如图(a)所示,一列简谐横波沿x轴传播,实线和虚线分别为t1时刻和t2时刻的波形图,其中t2>t1,P、Q分别是平衡位置为x1=1.0m和x2=4.0 m的两质点。图(b)为质点Q的振动图像,下列说法正确的是( )
A.t2-t1=0.1s
B.t2时刻Q的速度达到最大
C.简谐横波沿x轴传播的速度大小为40m/s
D.t1到t2内,P、Q运动的路程相等
3.在均匀介质绳中选取平衡位置在同一直线上的9个质点,相邻两质点的距离均为1m,如图(a)所示,一列简谐横波沿该直线向右传播,t=0时刚到达质点1,质点1开始向下运动,6s后第一次出现如图(b)所示的波形。对于该列波下列说法正确的是( )
A.周期T=6s B.波长=9m
C.波速=2m/s D.频率f=0.5Hz
4.一列简谐横波在t=s时的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图像。下列表述正确的是( )
A.这列波的传播方向为沿着x轴正方向
B.t=2 s时质点P的加速度方向沿着y轴负方向
C.这列波的传播速度大小为9 cm/s
D.质点Q的平衡位置横坐标为9 cm
5.一列简谐横波沿x轴传播,t=0.1s时的波形图如图甲所示,A、B为介质中的两质点。图乙为质点A的振动图像。以下判断正确的是( )
A.t=0.15s时,A的加速度为零
B.t=0.15s时,B的速度沿y轴正方向
C.从t=0.1s到t=0.25s,B的位移大小为10cm
D.从t=0.1s到t=0.25s,波沿x轴负方向传播了7.5m
6.图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x1=1m处的质点。Q是平衡位置为x2=4m处的质点,图乙为质点Q的振动图像,则( )
A.时,质点Q的加速度方向沿y轴负方向
B.该波沿x轴负方向传播,传播速度大小为20m/s
C.再经过0.10 s,质点Q沿波的传播方向移动4m
D.,质点P的位移是
7.图甲是一列简谐横波传播到x=5m的M点时的波形图,图乙是波形图上某质点从此时刻开始计时的振动图像,是位于x=10m处的质点,下列说法正确的是( )
A.乙图可能是x=1m处质点的振动图像 B.当点开始振动时,M点位于波谷
C.当点处于波峰时,N点的位移为0 D.经过3s,M点运动到x=8m处
8.图甲为一简谐横波在时刻的波形图像,图乙为横波中处质点的振动图像,下列说法正确的是( )
A.波的传播方向沿轴负方向
B.波的传播速度大小为0.01m/s
C.在时刻,质点的振动速度大小为0
D.在时刻,质点的振动加速度大小为0
9.如图所示,图甲为一列沿x轴传播的简谐横波在某时刻的波形图,P为平衡位置在的质点,图乙为此波中平衡位置坐标的质点从该时刻起的振动图像,下列说法中正确的是( )
A.波沿x轴负方向传播
B.由甲、乙两图可知该波波速为
C.从该时刻起,时,P点刚好经过平衡位置,振动方向向下
D.从该时刻起,P点第一次回到平衡位置通过的路程是
10.一列简谐横波沿x轴正方向传播,时波形如图所示。已知质点P再经过0.1s第一次到达波谷处,下列说法正确的是( )
A.这列简谐横波的波长是5m
B.这列简谐横波的波速是10m/s
C.质点Q要再经过0.2s才能第一次到达波峰处
D.质点Q到达波峰时质点P也恰好到达波峰
11.一列向右传播的横波在t=0时的波形如图所示,A、B两质点间距为8m,B、C两质点平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,该波的波速可能为( )
A.9m/s B.10m/s C.11m/s D.12m/s
12.一列简谐横波沿x轴传播,在t=0时刻的图像如图甲所示,介质中P质点的振动图像如图乙所示,下列说法正确的是( )
A.波沿x轴正方向传播
B.介质中质点振动周期为2s
C.波速大小为m/s
D.在t=2.5s时刻P、Q两质点的速度相同
13.均匀介质中,波源位于O点的简谐横波在xOy水平面内传播,波面为圆。t=0时刻,波面分布如图(a)所示,其中实线表示波峰,虚线表示相邻的波谷,A处质点的振动图像如图(b)所示,z轴正方向竖直向上,下列说法不正确的是( )
A.该波从A点传播到B点,所需时间为4s
B.t=6s时,B处质点位于波峰
C.t=8s时,C处质点振动速度方向竖直向上
D.E处质点起振后,12s内经过的路程为12cm
14.图甲为一列沿x轴传播的简谐横波在t=0.1 s时刻的波形图,图乙表示该波传播的介质中x=4 m处的质点b从t=0时起的振动图像,下列说法正确的是( )
A.波传播的速度为20 m/s
B.波沿x轴负方向传播
C.t=0.25 s时,x=2 m处的质点a的速度沿y轴正方向
D.从t=0至t=0.25s时间内,质点a通过的路程为1m
E.t=0.25 s时,质点a的加速度沿y轴负方向
15.一列简谐横波沿x轴传播,时的波形图如图甲所示,A、B为介质中的两质点。图乙为质点A的振动图像。以下判断正确的是( )
A.时,A的加速度为零
B.时,B的速度沿y轴正方向
C.从到的位移大小为
D.从到,波沿x轴负方向传播了
二、解答题
16.图甲为一简谐横波在t1=0.3 s时刻的波形图,图中M、N两点的平衡位置坐标分别为:xM=1 m,xN=5 m,此时波传到N点,平衡位置坐标x=1 m的质点M振动的图像如图乙所示,质点Q(图中未标出)的平衡位置距O点10 m。求:
(1)该波的波速;
(2)从t=0时刻开始计时,Q点位于波谷的时刻。
17.如图甲所示为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图。已知x=1m处的质点做简谐运动的图象如图乙所示。
(1)求波传播的速度大;
(2)从t=0时刻开始经过多长时间位于x=5m处的质点P开始振动?并求出在0~20s内质点P运动的路程。
参考答案
1.C
【详解】
当该列波向左传播时,根据题干可知1m和4m之间的距离满足的关系为
则由可得波速为
当n=0时,可得;当n=1时可得;
当波向右做传播时1m和4m之间的距离关系满足
则
当n=0时可得;当n=1时可得。故ABD正确,C错误。
本题选不可能的,故选C。
2.C
【详解】
A.因为没有说明t1时刻是哪个时刻,假设t1=0,根据图(b)可知,质点Q在t1时刻正在沿y轴正方向振动,则波向x轴正方向传播,可得
假设t1=0.1s,根据图(b)可知,质点Q在t1时刻正在沿y轴负方向振动,则波向x轴负方向传播,同理可得
故A错误;
B.由A分析可知,无论是哪种情况,t2时刻质点Q都在波峰,振动速度等于零,最小,故B错误;
C.由图可看出波长为8m,周期为0.2s,则波速为
故C正确;
D.t1到t2内, Q运动的路程可能是
或
如果t1=0,在第一个时间内,P沿y轴负方向运动到与x轴对称的位置,路程y1大于振幅A,则t1到t2内的路程
同理如果t1=0.1s,在第一个时间内,P沿y轴正方向运动到波峰,又沿y轴负方向回到原位置,路程y2小于振幅A,则t1到t2内的路程
可知P、Q运动的路程不相等,故D错误。
故选C。
3.C
【详解】
A.横波沿该直线向右传播,图示时刻质点9的振动方向向上,由题波源1的起振动方向向下,则第一次出现如图(b)所示的波形,振动传到质点9后,又传播了周期,则
解得
故A错误;
B.根据图(b)可读出波长为
故B错误;
C.波速为
故C正确;
D.频率为
故选C。
4.D
【详解】
A.当t=s时,Q向上振动,结合题图(a)可知,该波沿x轴负方向传播,故A错误;
B.t=2s时质点P处于平衡位置下方,其加速度方向沿着y轴正方向,故B错误;
C.由题图(a)可以看出,该波的波长λ=36 cm,由题图(b)可以看出周期为T=2 s,故波速为
v==18 cm/s
故C错误;
D.设质点P、Q的平衡位置的x轴分别为xP、xQ,由题图(a)可知,x=0处
y=-=Asin (-30°)
因此
xP=λ=3 cm
由题图(b)可知,在t=0时Q点处于平衡位置,经过Δt=s,其振动状态向x轴负方向传播到P点处,所以
xQ-xP=vΔt=6 cm
解得质点Q的平衡位置的x坐标为
xQ=9 cm
故D正确。
故选D。
5.D
【详解】
A.由题图乙可知,t=0.15s时,质点A处于波谷位置,则此时A的加速度最大,故A错误;
B.由题图乙可知在t=0.1s时质点A处于平衡位置且向下振动,由同侧法结合题图甲可知,波沿x轴负方向传播,由题图乙可知,波的周期为0.20s,则从题图甲所示t=0.1s时开始经过0.05s即个周期质点B处于平衡位置,速度方向沿y轴负方向,故B错误;
C.从t=0.1s到t=0.25s经历了个周期,质点B处于平衡位置,则B的位移为0,故C错误;
D.由题图甲可知,波长λ=10m,由题图乙可知,波的周期为0.20s,则波速为
v==m/s=50m/s
从t=0.1s到t=0.25s,波沿x轴负方向传播了
s=50×0.15m=7.5m
故D正确。
故选D。
6.D
【详解】
A.从乙图可以看出,时,质点Q的加速度方向沿y轴正方向,故A错误;
B. t=0.10s时刻Q沿y轴负方向运动,所以甲图中的波形向左传播,波速为
故B错误;
C.质点在平衡位置往复运动,不随波移动,故C错误;
D.由Q质点的振动图象可得其振动y-t关系式为
P比Q质点滞后八分之三周期,所以P质点的振动y-t关系式为:
将代入可得
故D正确。
故选D。
7.C
【详解】
A.由甲图可知,简谐横波沿x轴正方向传播,此时x=1m处的质点向y轴正方向振动,而乙图t=0时,该质点向y轴负方向振动,故A错误;
B.由甲图可知波长
由乙图可知周期
则波速为
波从M传播到Q的时间
此时M点在平衡位置向y轴正方向振动,经过,M点位于波峰。故B错误;
C.由甲图可知
所以当点处于波峰时,N点的位移为0,故C正确;
D.M点在平衡位置附近振动,不随波迁移,故D错误。
故选C。
8.B
【详解】
A.由图乙可知,时刻,质点向上振动,根据振动方向和波动方向的关系,可以判断出波的传播方向沿轴正方向,故A错误;
B.由图甲可知波长为4cm,由图乙可知周期为4s,波长、周期和波速的关系
故B正确;
C. 在时刻,质点的振动速度为图像的切线,因此速度不为零,故C错误;
D.在时刻,质点处于波峰,加速度最大,故D错误。
故选B。
9.D
【详解】
A.由图乙可知,时刻平衡位置坐标为的质点向下振动,由同侧法可知,该波沿x轴正方向传播,故A错误;
B.由图甲可得
由图乙可得
波速
故B错误;
C.由同侧发法可知,此时P点向上振动,要使P点刚好经过平衡位置,振动方向向下,波需要传播的距离为
所以时间为
可知无论取何值,都不可能等于,故C错误;
D.该波的表达式为
当时
由图可知,0时刻,P点向上振动,P点第一次回到平衡位置通过的路程
故D正确。
故选D。
10.B
【详解】
A.由波形图可知,这列简谐波的波长是4m,故A错误;
B.沿x轴正方向传播,则质点P向y轴负方向运动,由于质点P再经过0.1s第一次到达波谷处,可知波的周期为T=0.4s,则波速为
故B正确;
C.波从图示位置传播到质点Q需要用时
质点Q起振方向沿y轴负方向,从起振到第一次到达波峰需要的时间为t2=0.3s,所以质点Q要再经过0.5s才能第一次到达波峰,故C错误;
D.质点P再过0.5s到达波谷,故D错误。
故选B。
11.A
【详解】
由图可知,波长
波向右传播,质点C恰好通过平衡位置时,波传播的距离可能是或,则波速
或
当时
或
当时
或
故A可能,BCD不可能。
故选A。
12.C
【详解】
A.由题图乙可知,t=0时刻P质点向y轴负方向运动,由题图甲可判断波沿x轴负方向传播,故A错误;
B.设振动周期为T,由图乙可知
解得
T=3s
故B错误;
C.由题图甲可知波长,由波速公式可得波速
故C正确;
D.当P和Q关于平衡位置对称时,即处的质点恰在平衡位置时,P、Q两质点的速度相同,从时刻起,平衡位置的振动状态,向左传播至时处波传播的距离
经历的时间
可得
当n=0时有
t=1.25s
当n=1时有
t=2.75s
故D错误。
故选C。
13.ACD
【详解】
A.由图a可知,
则波长为
由图b可知,周期为
则波速为
因此从A传播到B需要的时间为
A正确;
B.波峰传到B点的时间为4s,该波在t=6s时即再经过,B位于波谷,B错误;
C.t=8s时,即再经过,根据几何关系可知
则
t=8s时,即经过2个周期,C处质点正在向波峰处运动,所有振动速度方向竖直向上,C正确;
D.由于
,
E经过的路程为
D正确。
故选ACD。
14.ADE
【详解】
A.由乙图知,质点的振动周期为T=0.2s,由甲图知,波长λ=4m,则波速为
故A正确;
B.由乙图知,t=0.1s时刻,质点b向上运动,根据甲图可知,该波沿x轴正方向传播,故B错误;
CE.由乙图知,质点的振动周期为T=0.2s,所以质点b在t=0.25s的时刻的振动情况与t=0.05s时刻的振动情况相同,即处于负的最大位移处,而质点a与质点b的间距为半个波长,所以a在正的最大位移处,加速度沿y轴负方向,速度为零,故C错误,E正确;
D.从t=0至t=0.25s时间内,质点a通过的路程为
故D正确。
故选ADE。
15.BD
【详解】
A.由图乙可知,t=0.15s时,质点A处于波谷位置,则此时A的加速度为最大,故A错误;
B.由图乙可知,波的周期为0.20s,则从图甲所示t=0.1s时到t=0.25s经过0.15s即四分之三周期质点B处于平衡位置,速度方向沿y轴正方向,故B正确;
C.从t=0.1s到t=0.25s经历四分之三周期,质点B处于平衡位置,则B的位移为5cm,故C错误;
D.由图乙可知在t=0.1s时质点A处于平衡位置且向下振动,波沿x轴负方向传播,由图甲可知,波长λ=10cm,由图乙可知,波的周期为0.20s,则波速为
从t=0.1s到t=0.25s,波沿x轴负方向传播了
s=50×0.15cm=7.5cm
故D正确。
故选BD。
16.(1) 10 m/s;(2) t=(0.4n+1.1) s,n=0、1、2、3、…
【详解】
(1)据题图甲可知
λ=4 m
据题图乙可得
T=0.4 s
故波速
v==10 m/s
(2)波谷从x=2 m处第一次传播到Q处所需时间
Δt==0.8 s
质点Q第一次到达波谷的时刻为
t′=(0.3+0.8) s=1.1 s
故Q点处于波谷的时刻为
t=(0.4n+1.1) s,n=0、1、2、3、…
17.(1)0.5m/s;(2)6s;28cm
【详解】
(1)由题图乙可知,振幅A=2cm,质点做简谐运动的周期为T=4s,波传播的周期也为T=4s,由题图甲可知波长λ=2m,波速
v==0.5m/s
(2)由题图甲可知,x=2m处的质点在t=0时刻刚好开始沿y轴负方向振动,设再经过Δt时间质点P开始振动,则
Δt==6s
即从t=0时刻开始经过6s时间质点P开始振动,由简谐运动的对称性可知,质点在任意一个全振动过程中的路程
s0=4A=8cm
质点P开始振动后14s内经历了3.5次全振动,所以在0~20s内质点P运动的路程为
s=3.5s0=28cm
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
