2021-2022学年人教版八年级数学下册17.1.1勾股定理 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1.1勾股定理 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 988.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
第十七章 勾股定理
17.1.1 勾股定理
情境引入
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家砖铺成的地面图案反映了直角三角形的某种数量关系。我们也来观察一下地面的图案,看看能从中发现什么(如图):
探究
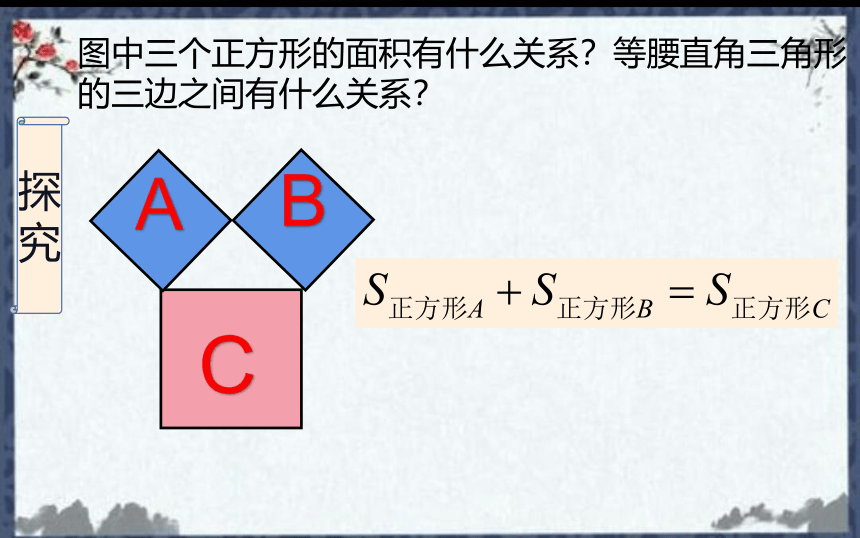
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
探究
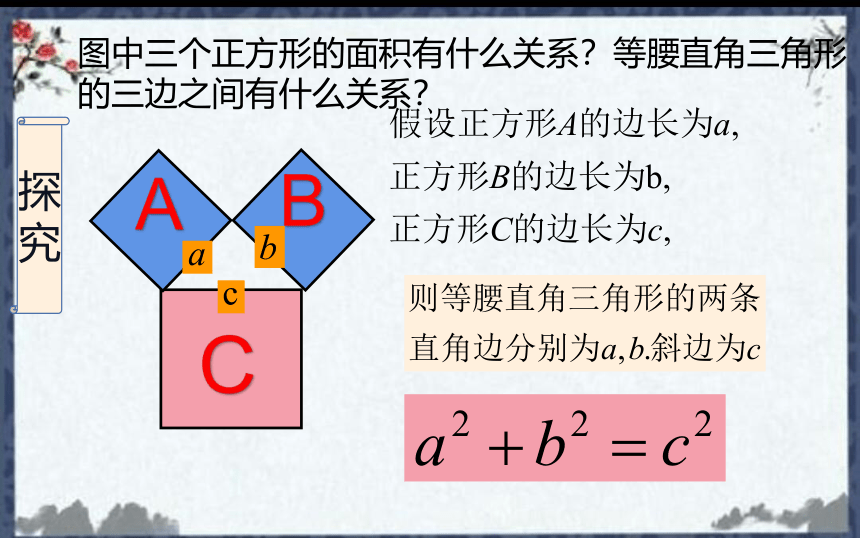
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
探究
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
探究
毕达哥拉斯的发现只是等腰直角三角形,其它的直角三角形是否也有这样的关系呢?
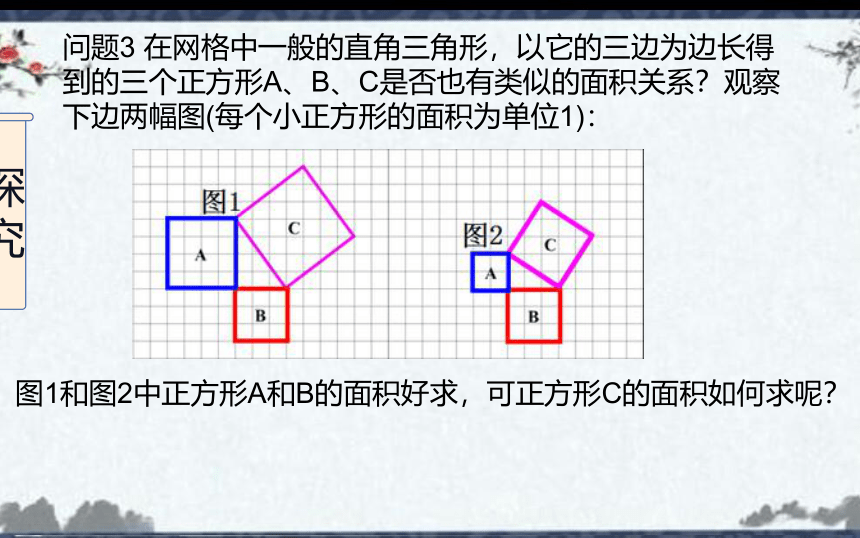
问题3 在网格中一般的直角三角形,以它的三边为边长得到的三个正方形A、B、C是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
探究
图1和图2中正方形A和B的面积好求,可正方形C的面积如何求呢?
探究
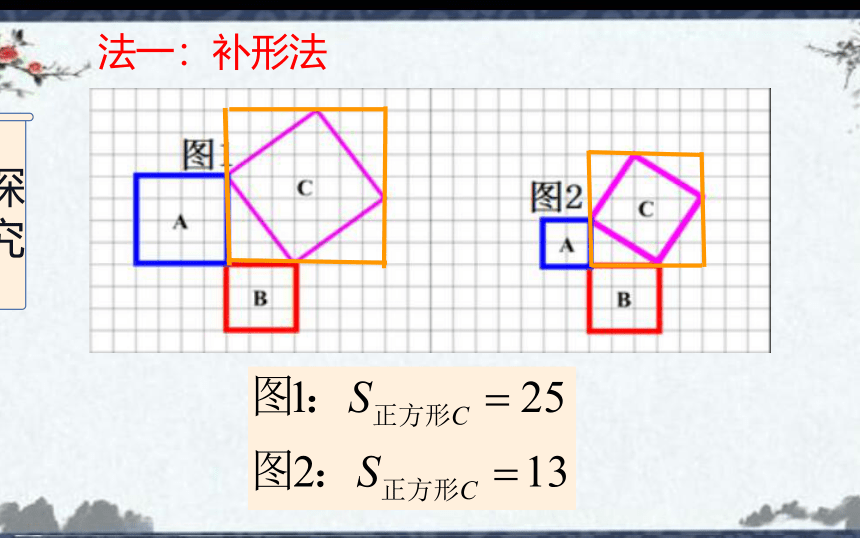
法一:补形法
探究
法二:分割法
探究
探究
探索新知
由上面的几个例子,我们猜想:
B
C
A
∟
B
C
A
∟
证法一:赵爽弦图
面积:
赵爽弦图
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
证法二:毕达哥拉斯法
用四个全等的直角三角形拼成一个大的正方形
证法二:毕达哥拉斯法
证法三:总统法
勾股定理
B
C
A
∟
B
C
练习
B
C
A
∟
B
C
D
练习
B
C
A
∟
B
C
D
练习
练习
B
C
A
∟
第十七章 勾股定理
17.1.1 勾股定理
情境引入
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家砖铺成的地面图案反映了直角三角形的某种数量关系。我们也来观察一下地面的图案,看看能从中发现什么(如图):
探究
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
探究
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
探究
图中三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
探究
毕达哥拉斯的发现只是等腰直角三角形,其它的直角三角形是否也有这样的关系呢?
问题3 在网格中一般的直角三角形,以它的三边为边长得到的三个正方形A、B、C是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
探究
图1和图2中正方形A和B的面积好求,可正方形C的面积如何求呢?
探究
法一:补形法
探究
法二:分割法
探究
探究
探索新知
由上面的几个例子,我们猜想:
B
C
A
∟
B
C
A
∟
证法一:赵爽弦图
面积:
赵爽弦图
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
证法二:毕达哥拉斯法
用四个全等的直角三角形拼成一个大的正方形
证法二:毕达哥拉斯法
证法三:总统法
勾股定理
B
C
A
∟
B
C
练习
B
C
A
∟
B
C
D
练习
B
C
A
∟
B
C
D
练习
练习
B
C
A
∟
