2021-2022学年人教版八年级数学下册课件 17.1.2勾股定理的实际应用 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册课件 17.1.2勾股定理的实际应用 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 715.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 17:02:15 | ||
图片预览





文档简介
(共21张PPT)
勾股
定理
的
实际
应用
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过 为什么
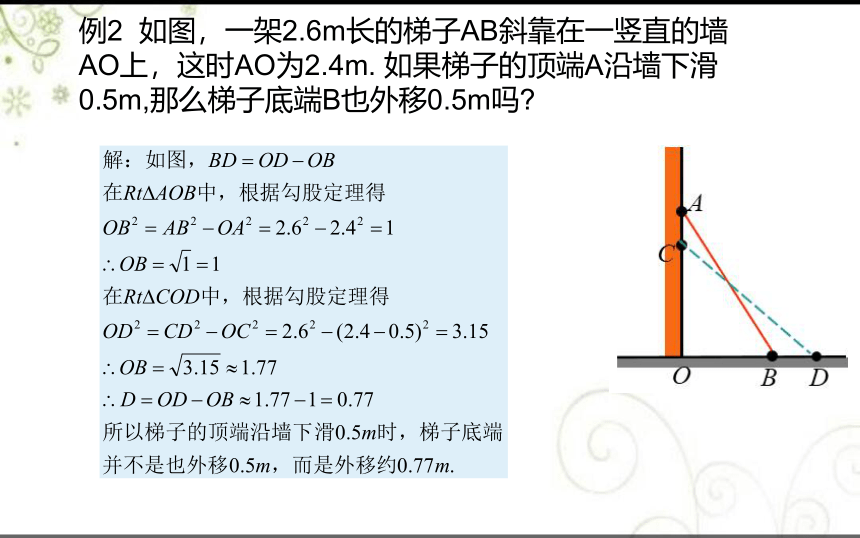
例2 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
如图,墙A处需要维修,A处距离墙脚C处8米,墙下是一条宽BC为6米的小河,现要架一架梯子维修A处的墙体,现有一架12米长的梯子,问这架梯子能否到达墙的A处?
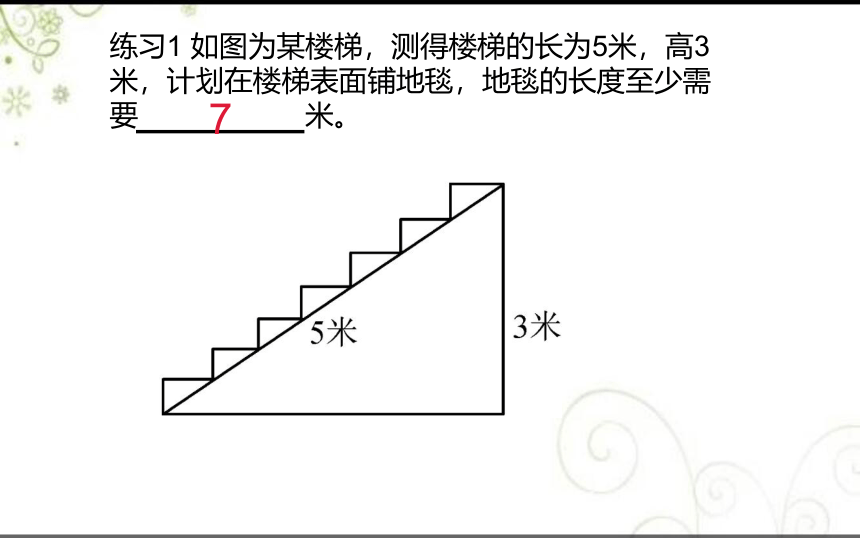
练习1 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米。
7
利用勾股定理求最短距离
如图,求点A到点B的最短路程
图1
图2
两点之间线段最短
图1和图2两个点所在位置的区别在哪里?
图1两个点在同一个平面内
图2两个点在不同的两个面
如何解决
把图形展开,
让两个点在
同一平面内。
如图,这是一个供滑板爱好者使用的U型池,该U型池可以
看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行
部分的截面半径为4m的半圆,其边缘AB=CD=20cm,点E
在CD上,CE=4m,一滑行爱好者从A点到E点,则他滑行的最
短距离为 。(π取整数)
20 m
如图,已知牛奶盒的长宽高分别为5cm、3cm、4cm,把小蚂蚁放在点A处,并在点B处放了一根棒棒糖,你能帮小蚂蚁找出吃到棒棒糖的最短路程么?
如图,第一种展开法
如图,第二种展开法
如图,第三种展开法
如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内
玻璃杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在
杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外
壁A处到B处的最短距离为 cm.(杯壁厚度不计)
20
如图,在等边三角形ABC中,D是BC的中点,E是AB的
中点,H是AD上任意一点。如果AB=AC=BC=10,那么
HE+HB的最小值是
H
5.如图,是一个三级台阶,它的每一级的长、宽和高分别等于24cm,4cm和2cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
C
6. 为筹备迎接新生晚会,同学们设计了一个圆筒形灯罩,用绿色丝带缠绕圆筒形灯罩,如图.已知圆筒的高为108cm,其横截面周长为36cm,如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸?
勾股
定理
的
实际
应用
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过 为什么
例2 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
如图,墙A处需要维修,A处距离墙脚C处8米,墙下是一条宽BC为6米的小河,现要架一架梯子维修A处的墙体,现有一架12米长的梯子,问这架梯子能否到达墙的A处?
练习1 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米。
7
利用勾股定理求最短距离
如图,求点A到点B的最短路程
图1
图2
两点之间线段最短
图1和图2两个点所在位置的区别在哪里?
图1两个点在同一个平面内
图2两个点在不同的两个面
如何解决
把图形展开,
让两个点在
同一平面内。
如图,这是一个供滑板爱好者使用的U型池,该U型池可以
看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行
部分的截面半径为4m的半圆,其边缘AB=CD=20cm,点E
在CD上,CE=4m,一滑行爱好者从A点到E点,则他滑行的最
短距离为 。(π取整数)
20 m
如图,已知牛奶盒的长宽高分别为5cm、3cm、4cm,把小蚂蚁放在点A处,并在点B处放了一根棒棒糖,你能帮小蚂蚁找出吃到棒棒糖的最短路程么?
如图,第一种展开法
如图,第二种展开法
如图,第三种展开法
如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内
玻璃杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在
杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外
壁A处到B处的最短距离为 cm.(杯壁厚度不计)
20
如图,在等边三角形ABC中,D是BC的中点,E是AB的
中点,H是AD上任意一点。如果AB=AC=BC=10,那么
HE+HB的最小值是
H
5.如图,是一个三级台阶,它的每一级的长、宽和高分别等于24cm,4cm和2cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
C
6. 为筹备迎接新生晚会,同学们设计了一个圆筒形灯罩,用绿色丝带缠绕圆筒形灯罩,如图.已知圆筒的高为108cm,其横截面周长为36cm,如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸?
